Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Using an Electronic Speckle Interferometry 199

The weld section is shown in Fig. 10a by grey ovals. In weld neighbourhoods

one can see the peaks of stresses.

The next drawing (Fig. 11) illustrates an influence of technology of repair

welded joints on levels of the residual stresses. Two such repair "patches" on a gas

pipe with the optical block of an electronic speckle interferometer installed on

them are shown in Fig.11a. A part of a thick-wall (thickness of 100 mm) chemical

reactor with a repair weld and the optical block of a speckle interferometer in-

stalled on it is shown in Fig. 11b. The repair niches cutting out on the place of

flaws, were filled according to different technologies by longitudinal or transverse

welds. The characteristic cases of filling up of repair niches are shown in Fig.

11c,d (thirteen narrow longitudinal welds superimposed in the conditions of the

continuous heat-conducting path (Fig. 11c) and two wide longitudinal welds (Fig.

11d)). The measured residual stresses differed almost on 50% at identical volumes

of filling up of niches levels. Smaller stress values were observed at filling up of a

niche with a considerable amount of thin welds (max

= 120 MPa). This result

testifies partial neutralization of stresses in welding layers (the direction of the

peak tensile stresses is shown in Fig. 11b by an arrow.

Fig. 11. The influence of technology of repair welded joints on levels of the residual

stresses: a - repair "patches" on a gas pipe, b - a part of a chemical reactor wall with a repair

weld, с, d - the maximal stresses at thirteen and two repair welds

The given and other examples show that the possibility of express-diagnostics

of the residual stresses allows to solve the problems on an influence of various

technological operations on SDS. Hence, the method and device can serve as a ba-

sis for development of optimal technological conditions of fabrication and treat-

ment of products, to reveal places of a structure dangerous from the strength point

of view, to develop recommendations for reducing the levels of these stresses and

to verify the efficiency of the recommendations.

200 R.V. Goldstein, V.M. Kozintsev, and A.L. Popov

3 Other Applications of Use ESPI

Along with determination of the residual stresses, the method and electronic

speckle interferometry equipment are successfully used for solving other prob-

lems. We will point out some of them:

• monitoring of evolution of residual stresses;

• determination of elastic characteristics of homogeneous and composite mate-

rials;

• diagnostics of delamination in multilayered thin coatings; evaluation of elas-

tic parameters of layers and shrinkage stresses;

• diagnostics of nanoscale displacements;

• using the electronic speckle interferometry in the sensor system for registra-

tion of physical fields of low intensity.

One of the representative problem of the list is the problem on searching for the

value of a force and a point of its application to the invisible side of a plate using

the observed data on number of interference fringes of microdisplacements and

their pattern at the visible side of a plate. In this case the loaded plate serves as a

sensitive element [6, 7].

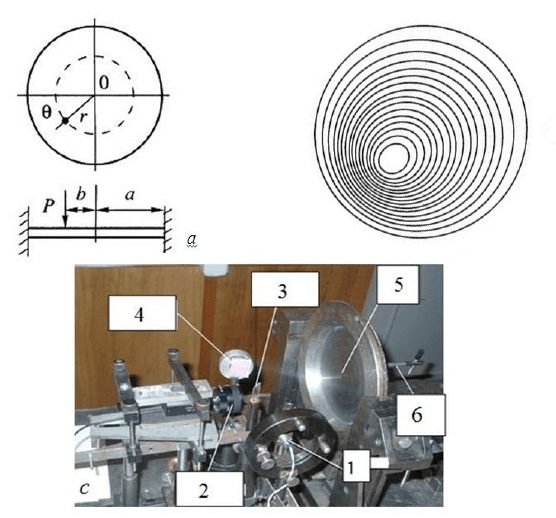
The calculated scheme of the problem on the noncentral application of normal con-

centrated force Р to the round rigidly clamped plate of radius a is given in Fig. 12a.

Fig. 12. Solution of a problem of searching for value of the force and point of its applica-

tion: a - the calculated scheme, b - level lines of the plate deflection, с - experimental setup

(1 - the laser, 2 - the video camera, 3 - the split mirror, 4 - a diffusely reflecting surface, 5 -

a round plate, 6 - the loading device)

Using an Electronic Speckle Interferometry 201

Calculated level lines of the plate deflection (w), received by means of the unique

closed formula by J.H. Michell [8] are shown in Fig. 12b.

where r, θ are the polar coordinates referenced from the center of a plate ξ=r/a,

=b/a, b is the distance from a plate center to the point of force action (in this case

b=0,4a), D is the cylindrical stiffness of a plate. Similar level lines of a deflection

of a plate in the form of a system of closed interference fringes are also obtained

by means of a pilot experimental system given in a Fig. 12c. Its optical part repre-

sents a modified scheme by Michelson (1 - the laser, 2 - the video camera, 3 - the

split mirror, 4 - a diffusely reflecting surface, 5 - a round plate, 6 - the loading de-

vice). The pattern of fringes and their number univalently determine the parame-

ters of a concentrated force.

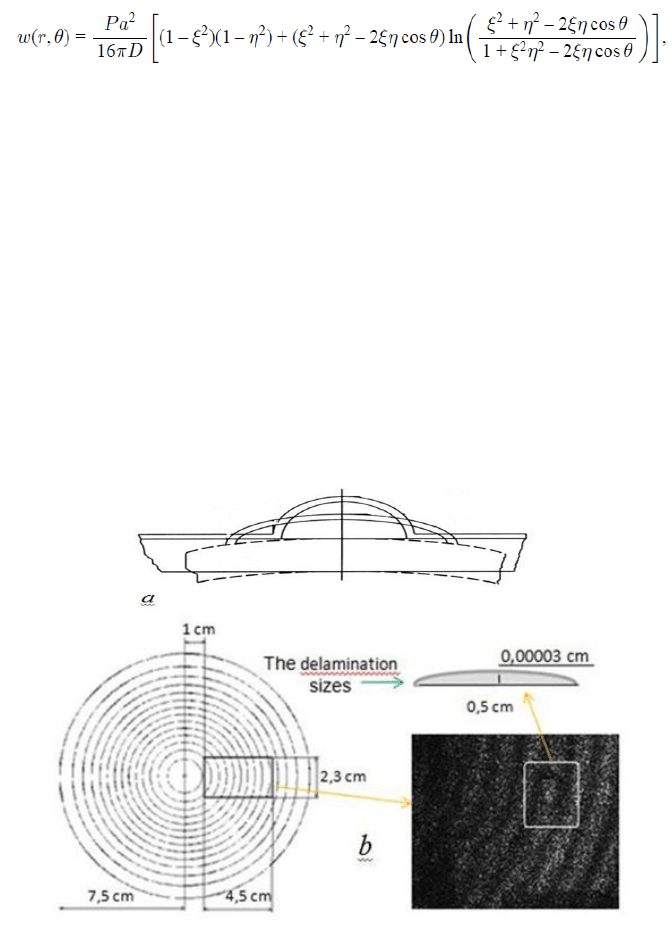
On the same plate used as a substrate, the possibility of registration of small

delaminations of a thin coating is shown. The method implies comparison of a refer-

ence state of a substrate with a coating (shown by the straight lines and a semicir-

cle delamination) with the state after a substrate bending (shown by dashed lines

and oval delamination), see Fig. 13a. The displacements in the delamination zone

at bending differ from displacements of a coating part without delamination [6].

On an interferogram it is shown by local distortion of the fringes form. Level lines

Fig. 13. Registration of small delaminations of a thin coating: a - displacements in the de-

lamination zone at bending differ from displacements of a coating part without delamina-

tion; b - delamination on an interferogram

202 R.V. Goldstein, V.M. Kozintsev, and A.L. Popov

max

16EJ

FhlF

of an axially symmetric deflection of a plate are shown in Fig. 13b at application

of a force at its center. In a certain place of the selected rectangular interval of a

plate with the sides 4,5 on 2,3 cm, a delamination invisible by an eye has been

created. After a substrate bending this delamination was detected in the form of an

oval between the adjacent interference fringes (it is marked by a white rectangle).

Thereby, its location and the linear dimensions were determined. The displace-

ments are in limits of a step of fringes, which is known if the value of the applied

force is known.

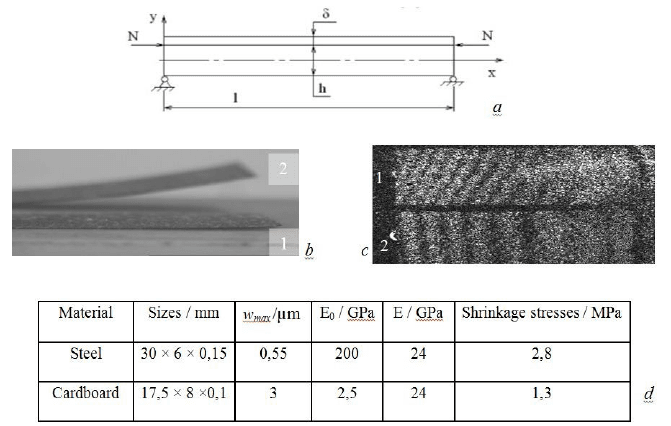
The shrinkage stresses arising after deposition of a thin coating on a substrate can

be estimated [6, 9] by the similar method implying the substrate bending. The model

of a rodlike substrate of length l and thickness h , hinge-supported at the edges

x=0,l with the coating of thickness δ<<h is superimposed is shown in Fig. 14a.

After the coating deposition its shrinkage occurs leading to generation of stresses in

a substrate and a coating film. A substrate bending is caused by the influence of

these stresses. Assuming that contraction of a coating without a substrate would

have the value Δl, it is possible to estimate the appropriate longitudinal force N con-

straining these contraction: N=EFΔl/l, where F is the section area, E is the coating

modulus of elasticity. The force N leads to the equivalent bending moment in a

substrate: M=Nh/2 and a deflection which in case of a hinge-supported rod has

the maximum value w

max

=Ml

/(8E

J) where E

is the modulus of elasticity of a

substrate, J is the inertia moment of inertia of its cross-section.

Hence, having measured a substrate deflection by means of an electronic

speckle interferometer, we can evaluate the shrinkage stresses in a coating

Note, that this formula does not include a coating modulus of elasticity, i.e., the

stress in a coating are determined by the given algorithm even if the basic elastic

characteristic of the coating is not known.

Clear representation of coating action on a substrate is given in Fig. 14b. There

are shown steel (1) and cardboard (made of a punched card) (2) beams after a

bending caused by contraction of an aerosol paint, superimposed on one of front

sides of beams.

Elastic characteristics of a coating are not determined by the given algorithm

directly. For their determination one needs to compare the flexural stiffnesses of

the coated and uncoated beams. Interferograms of a bending of identical cantilever

beams from a board are shown in Fig. 14c: 1 - with a coating of thickness of

0,01mm, 2 - without a coating. In both cases the loads at the free edges were

caused by mass of 4 mg.

As an example of determined moduli of elasticity and shrinkage stresses in

coatings, the table of their values taken from [6] is given in Fig. 14d.

One of the most interesting directions of development of the ESPI method is re-

lated to its extension for measurement of nanometer displacements and rates of

these displacements. The idea of registration of such displacements consists in in-

sertion in a set of informative parameters small changes in positions of level lines

of preliminary induced microdisplacements which lead to shifts of fringes without

Using an Electronic Speckle Interferometry 203

Fig. 14. Determination of shrinkage stresses in a thin coating: a - the calculated scheme, b -

steel (1) and cardboard (2) beams after a bending caused by contraction of an aerosol paint,

с - interferograms of a bending of beams (1 - with a coating, 2 - without a coating), d -

moduli of elasticity and shrinkage stresses in coatings

changing the total number of observable fringes [10]. It is possible to evaluate the

order of normal displacements registered by the method, for instance, follow a

bending of a cantilever beam such that the length of the observation area along the

beam axis is more than 10 millimeters while a difference of heights on this basis is

mapped by several (three-four) interference fringes, equals ~ 1 micron. As, the

digitized image of the observation area, pitched to the monitor screen from the

standard video camera of a DVD-format, represents a matrix of bright points (pix-

els) with the sizes about 800 pixels across on 600 on a vertical. Hence, the screen

distance between fringes at a small number of fringes equals hundreds pixels, in

particular, about 300 pixels for two fringes. Thus, difference of height in the form

of a deflection between the adjacent fringes of the same type, being equal 266 na-

nometers, is related to 300 pixels on the screen. Hence, registration of a fringe

shift of the minimal distinguishable value, 1 pixel of the screen resolution of an in-

terferogram, corresponds to additional small normal displacement of a beam of

order of 1 nanometers in a place of a fringe shift.

Metrological testing of measurements of the nanodisplacements using the de-

scribed method, was performed on the equipment presented in Fig. 15 (a is the

general view, b is the kinematic scheme).

The optical block of the equipment (1) related to the Leith-Upatnieks scheme

was almost the same, as was used for measurements of the residual stresses. For

204 R.V. Goldstein, V.M. Kozintsev, and A.L. Popov

(1)( )

mnn

−+

the high-precision assignment of supersmall displacements and velocities in the

field of the observation, limited in Fig. 15b by vertical dashed lines, we used the

two-cascade girder reduction gear transmitting a rotation from a cam (2), fayed on

an axis of an hour hand of a quartz clock, through two unequal-arm beams (3, 4)

with a proportion of shoulders of order 1/30 for everyone. As a result, the angular

velocity of a cam equals 30 grade/hour, is decreased to a zone of observation of an

interferometer approximately in 1000 times. This provides displacements of edges

of this zone during 5s within 10 nanometers if the image processing of speckle in-

terferograms can be done with an interval equals 0,5s.

Fig. 15. Metrological testing of measurements of the nanodisplacements (a is the general

view, b is the kinematic scheme of the equipment)

The typical speckle interferogram of displacements is given in Fig. 16 ((a) -

beam displacements in the field of observation; (b, c) - stages of fringe centers

separation). First, averaging of values of brightnesses through the columns of a

matrix of the interferogram image is performed (b), then a band-pass filtration of

this averaged brightness profile (c) is made (on the abscissa axis in Fig. 16 b,c co-

ordinates of columns of a numerical matrix of an electronic speckle interferogram

in screen pixels are put aside, while on the ordinate axis the values of brightness

according to eight-bit scale are given). Note, that the stage of averaging of bright-

ness along interferogram fringes provides an essential decrease of the speckle-

noise attaining hundreds of percents in line cross sections of an interferogram, to

the level of order 10%. This level is enough low for confident using known filtra-

tion methods.

Extremums of filtered brightness of an interferogram profile are identified as

centers of interference bands. Determination of nanodisplacements in places of

shifts of these centers is performed by the formula:

Using an Electronic Speckle Interferometry 205

where w is the value of the displacement of the body surface, λ is the laser wave-

length, m is the amount of stocked fringes ( m ≥ 2 ), N is the number of pixels be-

tween centers of maximally remote fringes from taking into account, n

is the

number of pixels corresponding to equal shift of centers of fringes which charac-

terizes the displacement of rigid body, n

is the number of pixels corresponding to

differential shift between fringe centers which characterizes variation of angle of

inclination.

Fig. 16. Determination of fringe center: a - speckle interferogram of beam displacements, b,

c - stages of fringe centers separation.

Comparing the set of given and gauged measured displacements showed a high

degree of their correlation: the maximal differences did not exceed 0,5 nanome-

ters. Thereby, the possibility of using the suggested method of speckle-

interferometric measurement of displacements from the level of 1 nanometer and

angular velocities - from 0,03 grade/hour has been confirmed.

Acknowledgement

Compactness and mobility of the developed equipment, operationability of reali-

zation of SDS measurements and the given examples of measurements results

show ample opportunities and perspectives of the ESPI method for the solving a

set of problems of a statics and dynamics of solids.

206 R.V. Goldstein, V.M. Kozintsev, and A.L. Popov

References

1. Burch, J.M., Tokarski, M.J.: Production of Multiple Beam Fringes from Photographic

Scatteres. Optica Acta. 15(2), 101–111 (1968)

2. Butters, J.N., Leendertz, J.A.: Holographic and video techniques applied to engineer-

ing measurements. Meas Control (4), 349–354 (1971)

3. Macovski, A., Ramsey, S.D., Schaefer, L.F.: Time-lapse interferometry and contouring

using television systems. Appl. Opt. (10), 2722–2727 (1971)

4. Peters, W.H., Ranson, W.F.: Digital Imaging Techniques in Experimental Stress

Analysis. Opt. Eng. 21(3), 427–432 (1982)

5. Kirsch, G.: Die Theorie d. Elastizität u. d. Bedurfnisse d. Festigkeitslehre. Zeitchrift

Vevein Deutscher Ingenieure. B 42(29), 797–807 (1898)

6. Goldstein, R.V., Kozintsev, V.M., Podlesnyh, A.V., Popov, A.L., Chelyubeev, D.A.: A

method of an electronic speckle interferometry for the solution of some inverse prob-

lems of mechanics of elastic bodies. Mechanics of Solids (2), 5–13 (2006)

7. Tian-hua, X., Chao, J., Wen-cai, J., Hong-xia, Z., Da-gong, J., Yi-mo, Z.: Design and

experiment of electronic speckle shearing phase-shifting pattern interferometer. Opto-

electronics Letters 4(1), 59–61 (2008)

8. Timoshenko, S., Woinowsky-Krieger, S.: Theory of Plates and Shells. Mcgraw-Hill

Comp., N.Y. (1959)

9. Stoney, G.G.: The tension of metallic films, deposited by electrolysis. Proc. Roy Soc.

London Ser. A. 82(553), 172–175 (1909)

10. Goldstein, R.V., Kozintsev, V.M., Podlesnyh, A.V., Popov, A.L., Chelyubeev, D.A.:

Use of an electronic speckle interferometry for registration of nanodisplacements. Me-

chanics of Solids (4), 662–670 (2008)

Structural Integrity and Residual Strength

of Composites Exposed to Fire

George A. Kardomateas

School of Aerospace Engineering,

Georgia Institute of Technology,

Atlanta, Georgia 30332-0150, USA

george.kardomateas@aerospace.gatech.edu

Abstract. The compressive response of an axially restrained composite column,

which is exposed to a heat flux due to fire is studied by both analytical and ex-

perimental means. The column is exposed to fire from one-side and an analytical

approach is outlined for the resulting heat damage, the charred layer formation and

non-uniform transient temperature distribution. Due to the nonuniform stiffness

and the effect of the ensuing thermal moment, the structure behaves like an imper-

fect column, and responds by bending rather than buckling in the classical Euler

(bifurcation) sense. In order to verify the mechanical response, the compressive

buckling behavior of the same material subjected to simultaneous high intensity

surface heating and axial compressive loading were investigated experimentally in

a specially designed cone calorimeter. Experiments on the residual compressive

strength following exposure to fire are also conducted for a range of heat fluxes

and exposure times.

1 Introduction

Fiber reinforced polymeric composites are used extensively in aerospace, marine,

infrastructure and chemical processing applications. In these applications, fire

events and their resulting effects on the structural integrity, are of considerable

concern. In addition to the implications for design, quantitative information re-

garding the nature of the strength loss is required to make decisions regarding, for

example, the seaworthiness of a ship that has sustained fire damage.

Many of the thermal properties of composites related to fire have been thor-

oughly studied and are well understood, including ignition times, heat release

rates, smoke production rates and gas emissions [1-5]. However, little attention

has been given to the structural integrity issues. For example, one important gap

in the understanding of composites is their response and structural integrity due to

the combined effect of mechanical loading and thermal loading due to fire. An-

other important issue is their residual strength following exposure to fire of a

given intensity and for a given period of time. This paper addresses these issues,

208 G.A. Kardomateas

both from analysis and experiments, as far as compressive loading, which in an

otherwise purely mechanical loading (no fire) would lead to bifurcational (Euler)

buckling.

2 Temperature, Char Distribution and Thermal Buckling

Analysis

The problem of predicting the behavior of polymer composite materials exposed

to a fire environment may be divided into two different parts: internal and external

processes. The internal processes include all the physical and chemical processes,

which occur in any laminate. The external processes deal first with the determina-

tion of the shape, size and intensity of the flame in the boundary layer and, second,

with the heat transfer to the laminate and the surroundings. The finite element

model used in the paper to predict the behavior of composites in a fire environ-

ment is based on the mathematical model proposed by Henderson et al [6] and de-

veloped by Gibson et al [7] and Looyeh et al [8]. The non-linear partial differen-

tial equations that govern the behavior of the laminate in the fire have been solved

numerically using a mixed explicit-implicit finite element technique. Accordingly,

the remaining resin material vs. exposure time can be obtained. Based on the ex-

periments and calculations performed by Gibson et al [10], we assume that when

the residual resin context is less than 80%, the material can be treated as charred.

The predicted temperature and charred layer thickness distribution with time

along the thickness direction are obtained by the thermal finite element model just

discussed. Now the quasi-static assumption is made to analyze the thermal buck-

ling response of the column consisting of an undamaged layer and a charred layer,

as shown in Figure 1. The quasi-static assumption means at each different time,

the column is in an equilibrium state and the temperature distribution and the

charred layer thickness at that time obtained by the finite element model can be

used in the static buckling analysis. The length and total thickness of the column

are denoted by L and H respectively. The thickness of the undamaged layer is rep-

resented by l, which is dependent on the time, t. It is reasonable to assume that the

mechanical properties of the charred (fire-damaged) layer are negligible because

of the thermal decomposition of resin material; this assumption was also made by

Mouritz and Mathys [11]. Therefore, we only considered the undamaged layer in

the thermal buckling analysis; nevertheless, the temperature distribution in the un-

damaged region is influenced by the existence of the char layer. Based on the ap-

proach discussed, Figure 2 shows the resulting temperature distribution and Figure

3 the normalized charred layer thickness for a fire intensity of Q = 25 kW/m

Regarding the Young’s modulus, E, of the undamaged composite, it is well

known that the modulus of polymers depends strongly on the temperature and es-

pecially on how close the temperature is to the glass transition temperature, T

, of

the matrix. A recent paper by Kulcarni and Gibson [12] studied the effects of tem-

perature on the elastic modulus of E-glass/Vinyl-Ester composites. They provided

measurements of temperature dependence of the elastic modulus of the composite

in the range of 20

C to 140

C. The glass transition temperature of the matrix was