Коткин Г.Л., Сербо В.Г., Черных А.И. Лекции по аналитической механике
Подождите немного. Документ загружается.


L(ϕ, ˙ϕ, t) =
m
2
h
˙
l
2
(t) + l
2
(t) ˙ϕ
2
i
+ mgl(t) cos ϕ (12.6)
m
˙
l
2
(t)/2
˜
U
R
δr
δr
r = l(t) = const R r
R δr = 0 . (12.7)
m
¨
r = mg + R , (12.8)
r(t) R(t)
t
l(t) = const

ϕ R
(m
¨
r − mg) δr = 0 , (12.9)
ϕ
“
N
F
α
(r
1
, ..., r
N
, t) = 0, α = 1, ..., n, (12.10)
n
“
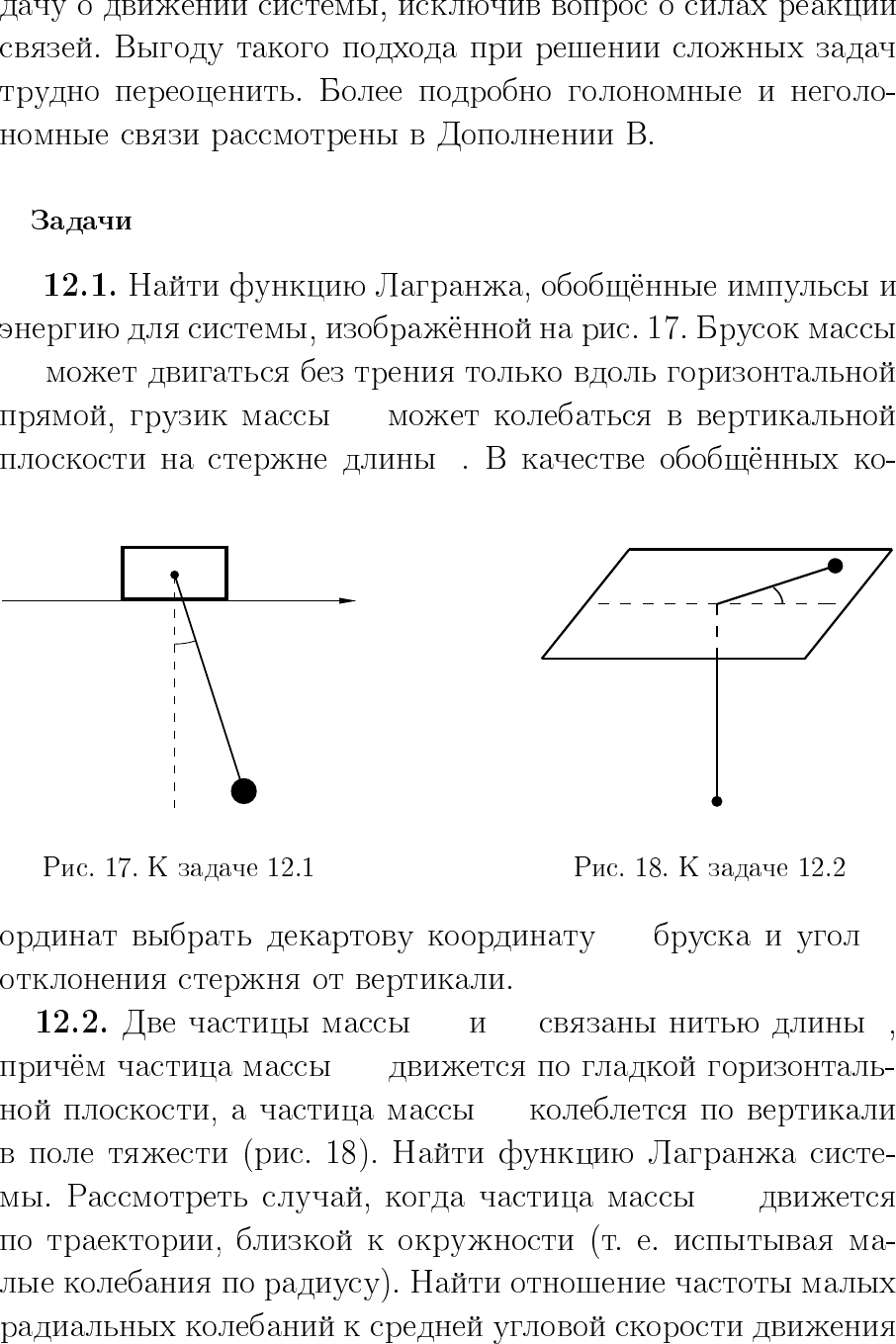
M
m
l
M
ϕ l
m
X
ϕ
m
r
M
X ϕ
M m l
M
m
M

§
ϕ
1
ϕ
2
y
x
l
1
m
1
l
2
m
2
ω
r
/h ˙ϕi
M = 3m
Ω

q
k
∂L
∂q
k
= 0 . (13.1)
p
k
= ∂L/∂ ˙q
k
dp
k
dt
=
d
dt
∂L
∂ ˙q
k
=
∂L
∂q
k
(13.2)
ϕ p
ϕ
= mr
2
˙ϕ sin
2
θ =
const.
dL
dt
=
X
i
∂L
∂q
i
˙q
i
+
∂L
∂ ˙q
i
d ˙q
i
dt
+
∂L
∂t
dL
dt
=
X
i
dp
i
dt
˙q
i
+ p
i
d ˙q
i
dt
+
∂L
∂t
=
d
dt
X
i
p
i
˙q
i
!
+
∂L
∂t
. (13.3)
E(t) =
X
i
p
i
˙q
i
− L =
X
i
∂L
∂ ˙q
i
˙q
i
− L , (13.4a)

a q
i
(t) ˙q
i
(t)
E
dE(t)
dt
= −
∂L
∂t
. (13.5)
∂L
∂t
= 0,
E(t) = const
L
2
L
1
L
0
L = L
2
+ L
1
+ L
0
, (13.6)
L
2
=
1
2
X
ik
a
ik
(q) ˙q
i
˙q
k
; L
1
=
X
i
b
i
(q) ˙q
i
; L
0
= L
0
(q, t) .
E = L
2
− L
0
, (13.7)
a
T + U
L
2
=
1
2
mv
2
L
1
=
e
c
Av

L
0
= − eϕ
E =
1
2
mv
2
+ eϕ , (13.8)
ω
ω
ϕ
m
l
T
T + U
L = T − U
ϕ
L(ϕ, ˙ϕ) =
1
2
ml
2
( ˙ϕ
2
+ ω
2
sin
2
ϕ) + mgl cos ϕ
E =
1
2
ml
2
( ˙ϕ
2
− ω
2
sin
2
ϕ) − mgl cos ϕ .
1
2
ml
2
ω
2
sin
2
ϕ
“
T +U
E

L L
′
F (q, t)
L
′
(q, ˙q, t) = L(q, ˙q, t) +
dF (q, t)
dt
.
E
a
E
′
(t) =
X
i
∂L
′
∂ ˙q
i
˙q
i
− L
′
, ( 1 3 .4 b)
E
′
(t) = E(t) −
∂F (q, t)
∂t
.
E E
′

U(r)
M
a z
ϕ → ϕ + ε ε
p
ϕ
= M
z
z
M
U(r)
E =
1
2
m
˙
r
2
+ U(r)
L(r,
˙
r, t) =
1
2
m
˙
r
2
− U(r)
t → t + ε ε
h z
ϕ → ϕ + ε , z → z +
h
2π
ε ,
ε z
ε
δL =
∂L
∂ϕ
ε +
∂L
∂z
h
2π
ε = 0 . (14.1)

∂L
∂ϕ
=
d
dt
∂L
∂ ˙ϕ
=
dp
ϕ
dt
,
∂L
∂z
=
d
dt
∂L
∂ ˙z
=
dp
z
dt
,
d
dt
p
ϕ
+
h
2π
p
z
= 0 ,
p
ϕ
= M
z
M
z
+
h
2π
p
z
= const . (14.2)
M
z
p
z
t → t + εc
t
, q
i
→ q
i
+ εc
i
, i = 1, 2, . . . , s , (14.3)
ε c
t
c
i
ε
δL = ε
∂L
∂t
c
t
+
s
X
i=1
∂L
∂q
i
c
i
!
= 0 . (14.4)
