Коткин Г.Л., Сербо В.Г., Черных А.И. Лекции по аналитической механике
Подождите немного. Документ загружается.


δU = k
1
x
2
/2
δU
xy
δU = k
1
x
2
/2
x(t) = a cos ω
1
t , y(t) = b sin ωt ,
(4.8)
ω
1
=
r
k + k
1
m
,
|x| ≤ a |y| ≤ b
δU = δU(x
2
+ y
2
)
δU = β/r
4
E
x
E
y

U =
U(|r
1
− r
2
|)
m
1
¨
r
1
= F(r
1
− r
2
) = −
∂U
∂r
1
, m
2
¨
r
2
= − F(r
1
− r
2
) (5.1)
r
1
r
2
R =
m
1
r
1
+ m
2
r
2
m
1
+ m
2
r = r
1
− r
2
¨
R = 0, m
¨
r = −
∂U(r)
∂r
, m =
m
1
m
2
m
1
+ m
2
. (5.2)
R =
R
0
+ Vt
m
F(r) = −
∂U(r)
∂r
.
z
R

U(r)
θ
R
ρ
dS = R
2
dΩ
dσ
z
n
v
∞
= (0, 0, v
∞
)
j = nv
∞
dS = R
2
dΩ
dΩ = sin θdθdϕ R
d
˙
N
j d
˙
N/j
U(r)
dS
dσ
z

v
∞
ρ = (ρ
x
, ρ
y
, 0)
dσ ≡ d
2
ρ = dρ
x
dρ
y
jdσ
d
˙
N
dS
dσ(θ, ϕ, E) =
d
˙
N(θ, ϕ, E)
j(E)
(6.1)
σ
dσ(θ, ϕ, E)
dΩ
=
d
2
ρ(θ, ϕ, E)
dΩ
(6.2)
σ dσ/dΩ
σ
F = −∇U(r)
˙
N

U(r) ∼ α/r
n
, n > 0
σ = ∞
R
1
R
2
ρ ≤ R
1
+ R
2
σ = π( R
1
+ R
2
)
2
U
ϕ
dσ(θ, E)
dΩ
=
d(πρ
2
)
2π sin θdθ
=
ρ(θ, E)
sin θ
dρ(θ, E)
dθ
. (6.3)
ρ(θ, E)

ρ(θ, ϕ, E)
θ ≪ 1 p =
(0, 0, mv
∞
) p
′
|p
′
| = |p |
θ ≈ sin θ =
p
′
⊥
p
, tg ϕ =
p
′
y
p
′
x
, (6.4)
p
′
⊥
= (p
′
x
, p
′
y
, 0) z
p
′
p
′
p
′
⊥
= ∆p
⊥
∆p =
p
′
− p
dp = Fdt
∆p =
Z
∞
−∞
F(t)dt = −
Z
∞
−∞
∂U(r(t))
∂r
dt .
r(t) = ρ + v
∞
t
p
′
⊥
= −
∂
∂ρ
Z
∞
−∞
U(ρ + v
∞
t) dt . (6.5)
U U(r) =
U
p
ρ
2
+ (v
∞
t)
2
ϕ
z = v
∞
t
θ =
1
2E
∂
∂ρ
Z
∞
−∞
U
p
ρ
2
+ z
2
dz
. (6.6)
ρ(θ, E) dσ/dΩ
U(r) =
α
√
r
2
+ a
2
E ≫
α
a
E
α/a
θ =
αρ
2E
Z
∞
−∞
dz
(ρ
2
+ z
2
+ a
2
)
3/2
=
α
E
ρ
ρ
2
+ a
2
.
θ
m
ρ = a
θ
m
=
α
2Ea
≪ 1 .
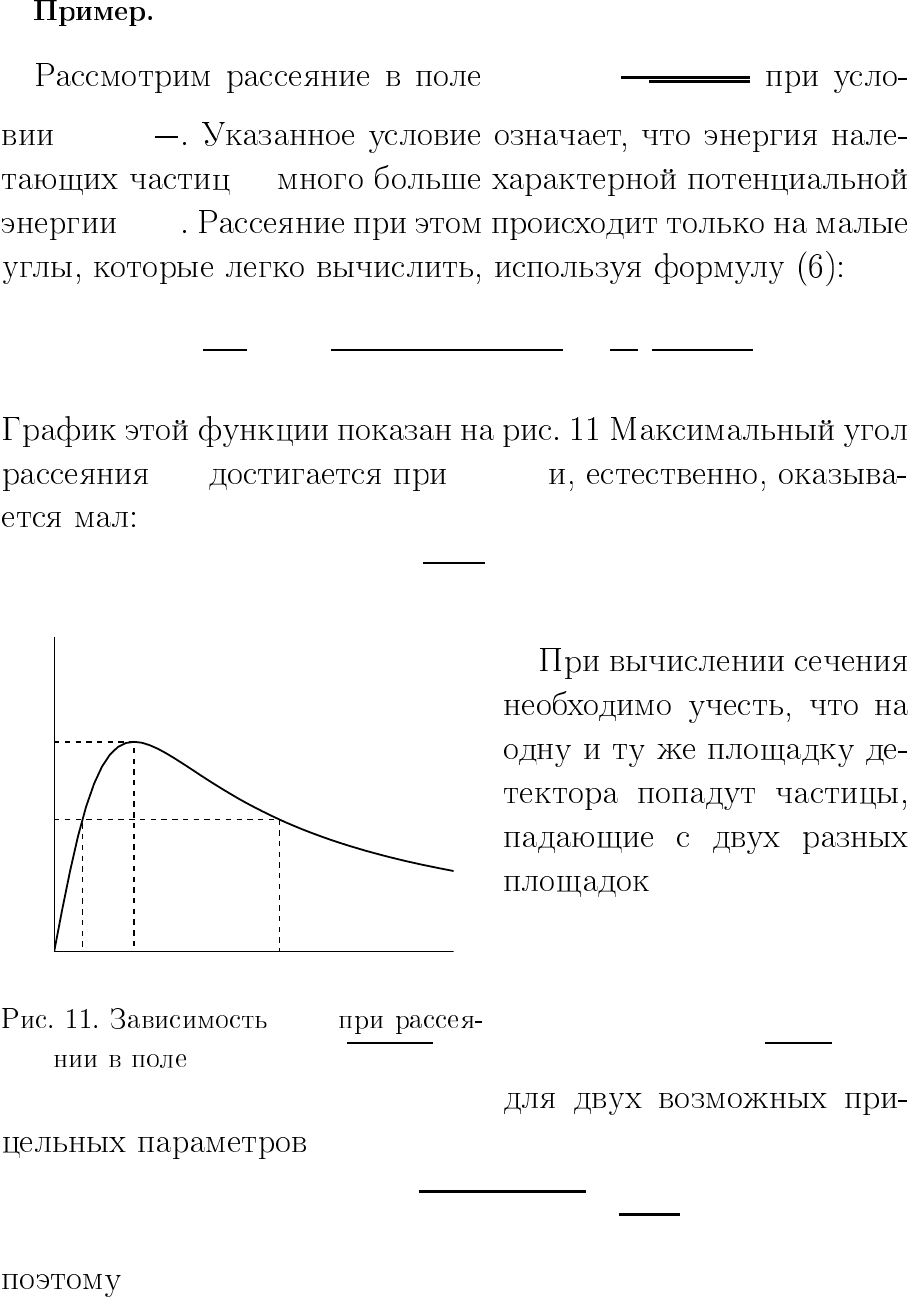
θ(ρ)
θ
m
θ
ρ
1
ρ
2
ρ
a
θ(ρ)
U(r) = α/
√
r
2
+ a
2
dσ
1,2
= π|dρ
2
1,2
| =
= ± dρ
2
1,2
= ± π
dρ
2
1,2
dθ
dθ
ρ
1,2
=
1 ∓
p
1 − (θ/θ
m
)
2
α
2Eθ
,
dσ = π
|dρ
2
1
| + | dρ
2
2
|
= πd
ρ
2
1
− ρ
2
2
=

dσ
dΩ
___
θ
θ
m
U(r) =
α
p
r
2
+ a
2
= πd [(ρ
1
− ρ
2
)(ρ
1
+ ρ
2
)] .
dσ
dΩ
=
α
2
E
2
θ
4
1 − θ
2
/(2θ
2
m
)
p
1 − (θ/θ
m
)
2
θ < θ
m
,
0 θ > θ
m
.
(6.7)
dσ/dΩ θ θ → 0
dσ/dΩ
dσ
dΩ
≈
α
2
E
2
θ
4
→ ∞ θ → 0 . (6.8)
θ = 0
dσ/dΩ
θ →θ
m
dσ
dΩ
≈
α
2
2
√
2E
2
θ
4
m
p
1 − (θ/θ
m
)
→ ∞ θ → θ
m
. (6.9)
θ
m

ρ = a
θ
m
− δ < θ < θ
m
Z
θ
m
θ
m
−δ
2π
dσ
dΩ
θ dθ =
πα
2
δ
1/2
√
2E
2
θ
5/2
m
,
δ → 0
U(r) = α/r
E = mv
2
∞
/2
ρ
ABC A C
θ
ϕ
B
A
B
C
x
ρ
U(r) = α/r
B
xy
r
ϕ
ABC
r(ϕ) =
p
−1 + e cos(ϕ − ϕ
B
)
, (6.10)
p e ϕ
B
B ϕ
A
ϕ
C
A
C θ ϕ
B
ϕ
A
= π , ϕ
C
= 2ϕ
B
− π = θ .
ϕ
B
r(ϕ
A
) = ∞
−1 + e cos(π − ϕ
B
) = 0
ϕ
B
=
π + θ
2
, M
2
= (mv
∞
ρ)
2
= 2mEρ
2
, e
2
= 1 +
2Eρ
α
2
,
ρ(θ) =
α
2E
ctg
θ
2
(6.11)
dσ
dΩ
=
α
4E
2
1
sin
4
(θ/2)
. (6.12)
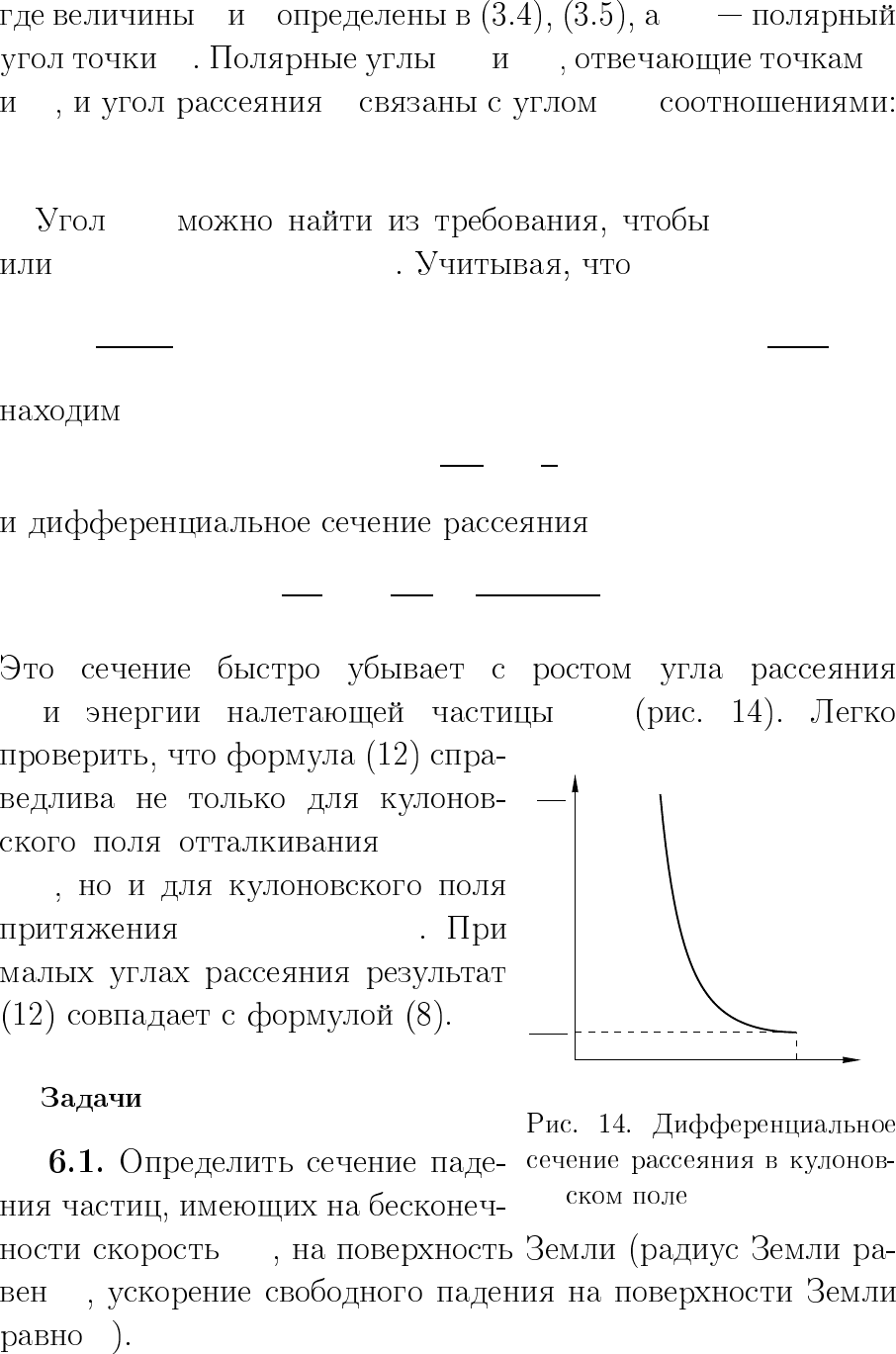
θ E
θπ0
α
2
4E
2
dσ
dΩ
U(r) = ±α/r
U(r) =
α/r
U(r) = −α/r
v
∞
R
g
