Koster A., Munoz X. Graphs and Algorithms in Communication Networks

Подождите немного. Документ загружается.

1 Graphs and Algorithms in Communication Networks on Seven League Boots 11

that has been in the cache the longest time without being requested. It can be shown

that First-In-First-Out and Least-Recently-Used are k-competitive [84]. Moreover,

it has been proved that no deterministic algorithm (i.e., an algorithm that does not

include randomized decisions) exists that is c-competitive with c < k [84].

Algorithms with a better performance can be obtained by using randomized deci-

sions. In particular, the random marking algorithm of [47] has a competitive ratio of

, where H

= 1+

+...+

is the kth Harmonic number (note that H

≤1+lnk.

The algorithm works in phases as follows. Initially all pages in the cache are un-

marked. A phase is ended as soon as all pages in the cache are marked. In this case,

all pages are unmarked and a new phase begins. This way, we always have at least

one page unmarked upon the arrival of a request for a page p. If page p is in the

cache, it is marked. If page p is not in the cache, we randomly choose an unmarked

page in the cache to be replaced by p, and p is marked.

We refer to [52] for further reading in the area of online optimization. Applica-

tions of online optimization in communication networks can be found in Chapters 2

and 10.

1.3 Computational Complexity

Computational Complexity theory is the science that studies the computational re-

sources (time, memory, etc.) needed to solve computational problems. It is espe-

cially concerned with the distinction between tractable problems, that can be solved

with reasonable amount of resources, and intractable problems, that are beyond the

power of existing, or conceivable, computers.

Obviously the computational resources needed to solve a problem depend on the

size of the problem input data. A problem is considered efﬁciently tractable if the

resources needed grow at most as a polynomial function in terms of the input data,

and is considered not efﬁciently computable otherwise.

A complexity class is the set of problems solvable by a particular computational

model under a given set of resource constraints. Therefore, if we focus on time as

the main resource, or equivalently, the number of elementary computer operations

required to solve the problem, we deﬁne a ﬁrst complexity class as follows.

P is the class of decision problems that can be solved in polynomial time on a

deterministic effective computing system (ECS). Loosely speaking, all computing

machines that currently exist in the real world are deterministic ECSs. So, P is the

class of problems that can be computed in polynomial time on real computers. A

decision problem is a problem for which the solution is a “yes” or “no” answer.

NP is the class of decision problems that can be solved in polynomial time on

non-deterministic ECSs. A non-deterministic machine is a machine which can ex-

ecute programs in a way where, whenever there are multiple choices, rather than

iterate through them one at a time it can follow all choices or paths at the same time,

and the computation will succeed if any of those paths succeed; if multiple paths

lead to success, one of them will be selected by some unspeciﬁed mechanism; we

12 A. M. C. A. Koster, X. Mu

noz

usually say that it will pick the ﬁrst path to lead to a successful or “yes” result. The

idea of non-determinism in effective computing systems can be explained without

entering into details of non-deterministic computing machines (the reader is referred

to [8, 50] for a more detailed explanation). A decision problem whose “yes” solution

can be computed in polynomial time on a non-deterministic machine is equivalent

to a problem where a proposed “yes” solution can be veriﬁed as correct in polyno-

mial time on a deterministic machine. You can specify a non-deterministic machine

that guesses one solution, following all of those paths at once, and returning a result

whenever it ﬁnds a solution that it can verify is correct. So, if you can check a so-

lution deterministically in polynomial time (not produce a solution, but just verify

that the solution is correct), then the problem is in NP.

The distinction can become much clearer with an example. A classic problem

is the subset sum problem. In the subset sum problem, an arbitrary set of integers

is given. The question is whether there exists a nonempty subset of values in the

set whose sum is 0? It should be pretty obvious that checking a solution is in P:a

solution is a list of integers whose maximum length is the size of the entire set; to

check a potential solution, add the values in the solution, and see if the result is 0.

The computational effort of this procedure is O(n) where n is the number of values

in the set. But ﬁnding a solution is hard. The solution could be any subset of any size

larger than 0; for a set of n elements, there are 2

−1 such subsets. Even if you use

clever tricks to reduce the number of possible solutions, you are still in exponential

territory in the worse case. But you can non-deterministically guess a solution and

test it in linear time; but no one has found any way of producing a correct solution

deterministically in less than

) steps.

One of the great unsolved problems in theoretical computer science is does P =

NP? That is, is the set of problems that can be solved in polynomial time on a

non-deterministic machine the same as the set of problems that can be solved in

polynomial time on a deterministic machine? It is clear that that P ⊆ NP, that is,

that all problems that can be solved in polynomial time on a deterministic machine

can also be solved in polynomial time on a non-deterministic machine. Although it

is a commonly accepted hypothesis that P = NP no one has been able to prove it to

date.

Within NP, there is a set of particularly interesting problems which are called

NP-complete. The idea of an NP-complete problem is that it is one of the hardest

problems in NP or, in other words, is one where we can prove that if there is a P-

time computation that solves the problem, it would mean that there was a P-time

solution for every problem in NP, and thus P = NP.

How do we show that a given problem is NP-complete? NP-completeness is

based on the idea of problem reduction. Given two problems S and T for which it

can be shown that any instance of S can be transformed into an instance of T in

polynomial time, it is said that S is polynomial-time reducible to T. Therefore, if an

efﬁcient algorithm to solve problem T is known, this algorithm can also be used to

solve problem S. It can be seen as S is easier than T .

Once we know a problem T which is NP-complete, then for any other problem

U, if we can show that T is polynomial-time reducible to U, then U must be NP-

1 Graphs and Algorithms in Communication Networks on Seven League Boots 13

complete as well. If we can reduce T to U, but we do not know how to reduce U to

T or we do not know if U ∈ NP, then we do not just say that U is NP-complete; we

say that it is NP-hard.

There are a lot of problems which have been proved NP-complete. So, given a

new problem, there are a lot of different NP-complete problems that can be used as

a springboard for proving that the new problem is also NP-complete.

Most NP-completeness proofs are ultimately built on top of the NP-completeness

proof of one fundamental problem, whose nature makes it particularly appropriate

as a universal reduction target and it is also the ﬁrst problem that was proved to be

NP-complete. It is called the propositional satisfaction problem (a.k.a. SAT or sat-

isﬁability), which was shown to be NP-complete via a rather abstract model (Cook

Theorem [50]). For any other problem, if we can show that we can translate any in-

stance of a SAT problem to an instance of some other problem in polynomial time,

then that other problem must also be NP-complete. And SAT (or one of its simpler

variations, 3-SAT) is particularly easy to work with, and it is easy to show how to

translate instances of SAT to instances of other problems.

Let us see an example. A vertex cover of an undirected graph G =(V,E) is a

subset V



of the vertices of the graph such that every edge in G has an endpoint in



, i.e., ∀(u,v) ∈ E : u ∈V



∨v ∈V



The vertex cover problem is the optimization problem of ﬁnding a vertex cover

of minimum size in a graph. The problem can also be stated as a decision problem:

Given a graph G and a positive integer k, is there a vertex cover of size k or less for

Vertex cover is closely related to the Independent Set problem: V



is a vertex

cover if and only if its complement, V \V



, is an independent set. It follows that a

graph with n vertices has a vertex cover of size k if and only if the graph has an

independent set of size n −k. Equivalently a graph G =(V,E) with n vertices has

a vertex cover of size k if and only if the complementary graph

G =(V, E) have

a clique of size n −k. This equivalence shows a trivial polynomial reduction from

clique to vertex cover. Since clique (does a graph has a clique of given size?) is an

NP-complete problem (see [50]), we have shown the NP-completeness of vertex

cover.

1.4 Combinatorial Optimization Methods

Given a (classical) combinatorial optimization problem by its three components,

the ground set E, (an implicit deﬁnition of) the feasible solutions F , and a weight

function w : E → Z, the problem can be formulated as mathematical optimization

problem by introducing decision variables for all elements of the ground set E.For

every e ∈ E the decision variable x

can take the values 0 or 1 (and is therefore

called binary) indicating whether e is chosen (1) or not (0) in the optimal solution.

Hence, the objective can be written as

∑

e∈E

. We further deﬁne x



=(x

)

e∈E

to be the incidence vector for a subset E



⊆E, i.e., x

= 1ife ∈ E



and 0 otherwise.

14 A. M. C. A. Koster, X. Mu

noz

By deﬁning X = {x



| E



∈ F }, we now can write the problem as

max



x |x ∈ X



. (1.2)

If convenient from the problem perspective, the above might be generalized to multi-

sets to represent decisions that can be made multiple times.

To ﬁnd an optimal solution for the above problem, a number of methods are avail-

able. In the following we ﬁrst introduce linear programming problems and brieﬂy

describe algorithms to solve such problems. Next, we discuss how combinatorial

optimization problems can be solved with linear-programming-based techniques.

Alternative solution methods like graph theory, problem-speciﬁc combinatorial al-

gorithms, approximation algorithms, and heuristics are discussed in Sections 1.4.2,

1.4.3, 1.4.4, and 1.4.5 respectively. Both linear-programming-based branch-and-

bound and graph algorithms are examples of exact algorithms, i.e., they provide

the optimal solution in the end. In contrast, heuristics and approximation algorithms

provide a good but not necessarily optimal solution.

Note that the above discussion becomes more complicated as soon as more gen-

eral problems are studied. A brief discussion of nonlinear optimization methods can

be found in Section 1.4.6

1.4.1 Linear-Programming-Based Methods

1.4.1.1 Polyhedral Theory

Since the components of all vectors x ∈ X are either 0 or 1, problem (1.2) is equiva-

lent to

max



x |x ∈ P



where P = conv(X) is the convex hull of all vectors in X, i.e.,

conv(X) :=



y |∃t ∈Z

,∃x

,...,x

∈ X, ∃

∈ [0, 1]

∑

i=1

= 1, y =

∑

i=1



AsetP that can be written as the convex hull of a ﬁnite number of vectors is called a

polytope.AsetP ⊂R

is called a polyhedron if and only if there exists m ≥0 such

that

P = {x ∈R

| Ax ≤ b},

where A is an m×n matrix and b ∈ R

(if m = 0, P = R

). A polytope is a bounded

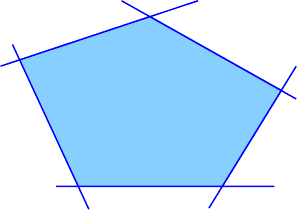
polyhedron. An example is given in Figure 1.3.

So, instead of an implicit description of all feasible solutions, we can give a

polyhedral description of the solutions by a system Ax ≤ b. In fact, in the case of

1 Graphs and Algorithms in Communication Networks on Seven League Boots 15

Fig. 1.3 A two-dimensional polyhedron described by a system of ﬁve inequalities

binary vectors describing the feasible solutions, the polyhedron is bounded. This fact

is the key to solving combinatorial optimization problems with linear programming

techniques.

In case the solutions are represented by multi-sets of the ground set E,asim-

ilar approach can be followed, with the difference that the solution space may be

unbounded (in theory), and therefore we have to study a polyhedron instead of a

polytope. Although not necessary if the objective is linear, it is usually assumed that

every integer solution that can be written as a convex combination of integer feasible

solutions is also feasible. This assumption is not needed in the case of binary vec-

tors since binary vectors cannot be written as a convex combination of other binary

vectors.

1.4.1.2 Solving Linear Programming Problems

A linear program (LP) is an optimization problem satisfying the following condi-

tions

• the objective is a linear function of the variables

• all constraints are linear in the variables

• the variables can take any values (i.e., ∈ R) that satisfy the constraints

By this deﬁnition, an LP can be written w. l. o. g. in its standard maximization form

as follows

⎧

⎨

⎩

max c

s.t. Ax = b

x ≥0

(1.3)

with matrix A ∈ Q

m×n

, a right-hand side b ∈ Q

, and arbitrary objective values

c ∈R

(here, m is the number of rows and n the number of columns of A). Objectives

to be minimized can be rewritten as a maximization problem by multiplying the co-

efﬁcients by -1. Likewise for equations with negative right-hand sides. Inequalities

can be written as equations by introducing slack variables. Upper bound constraints

for single variables are included in the coefﬁcient matrix (with a slack variable).

16 A. M. C. A. Koster, X. Mu

noz

Negative lower bounds can be avoided by substituting variables, and therefore we

can assume that all variables are nonnegative.

The optimal solution of a linear program (1.3) can be found by a variety of meth-

ods developed since the 1940s. A ﬁrst method is Fourier-Motzkin elimination for

solving systems of linear inequalities [82, Chapter 12], but it is computationally

rather intensive. More efﬁcient algorithms (either in theory or practice) are provided

by the Simplex method and interior point methods.

Simplex Method

The Simplex method was developed as early as 1947 by Dantzig [36]. Assuming

there exist feasible solutions to (1.3), the Simplex algorithm exploits the fact there

exists an optimal solution that is an extreme point (vertex) of the polyhedron deﬁned

by Ax = b and x ≥ 0. Therefore, the Simplex algorithm walks along the extreme

points of the polyhedron in such a way that the objective value of the sequentially

considered solutions is improving. For this a ﬁrst extreme point of the polyhedron

has to be found. This is known as Phase I, whereas the walk along the extreme

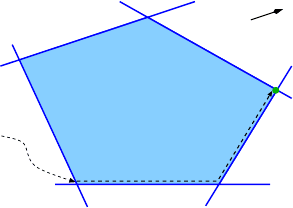
points of the polyhedron to an optimal solution is known as Phase II. Figure 1.4

illustrates the procedure for an objective and the polyhedron of Figure 1.3.

solution

objective

Phase I

Phase II

Fig. 1.4 Given an objective, at least one optimal solution is an extreme point of the polyhedron;

the Simplex method uses this property by walking along the extreme points

If b = 0, x = 0 is a feasible solution of (1.3). If b = 0, this solution is infeasible

and Phase I consists of setting up an auxiliary linear program for which a feasible

solution can be easily found. Next, Phase II is applied to this auxiliary LP to ﬁnd

a feasible solution of (1.3). The auxiliary LP is obtained by introducing variables

≥0, 1 ≤ i ≤ m. The aim is to ﬁnd a solution with s = 0, and thus the auxiliary LP

reads

⎧

⎨

⎩

max 1I

s.t. Ax + s = b

x,s ≥0

(1.4)

where 1I is the all-one vector of dimension m. It holds that (1.3) has a feasible solu-

tion if and only if the optimal solution of (1.4) has s = 0. A feasible solution of (1.4)

1 Graphs and Algorithms in Communication Networks on Seven League Boots 17

is given by (x,s)=(0,b) (note b ≥0 in (1.3)). So, we directly can start with Phase

II for this auxiliary LP. If the optimal solution (x

∗

) has s

∗

= 0, the polyhedron

deﬁned by Ax = b, x ≥0 is empty; otherwise, x

∗

is a feasible solution for (1.3).

Phase II works with basic feasible solutions. A basic solution to Ax = b (with

n ≥m) is obtained by setting n−m variables equal to 0 (the non-basic variables) and

solving the values of the remaining m variables (the basic variables), assuming that

the columns for the remaining m variables are linearly independent. If all variables

in a basic solution are nonnegative, it is called a basic feasible solution. It can be

shown that a point in the feasible region of LP (1.3) is an extreme point if and only

if it is a basic feasible solution to Ax = b. Now, two basic feasible solutions are said

to be adjacent if their sets of basic variables have m−1 basic variables in common.

Since an LP with a nonempty feasible region always has an optimal basic feasible

solution, the solution provided by Phase I is a basic feasible solution of (1.3). Start-

ing with this solution, the Phase II of the Simplex algorithm exchanges one basic

variable for a non-basic variable in order to become a better objective value. Such

an exchange is called a pivot. As long as the basic feasible solution is not optimal,

such a pivot exists. The performance of the Simplex algorithm heavily depends on

the selection of the pivot element (including so-called cycling between basic feasi-

ble solutions with the same objective value). An optimal solution is found as soon

as none of the neighboring basic feasible solutions have a better objective value (we

omit the technical details on how to check this condition here).

Klee and Minty [67] have shown that the Simplex algorithm might take an expo-

nential number of pivots to ﬁnd the optimal solution. In practice, however, revised

and dual versions the Simplex algorithm are still considered as the best algorithms

to solve linear programs [20]. For an in-depth introduction to the Simplex algorithm

we refer to [29, 88].

Interior Point Methods

The worst-case exponential behavior of the Simplex algorithm has motivated re-

search for alternative, polynomial time, algorithms to solve a linear program. Start-

ing with the work of Karmarkar [65], so-called interior point methods resolved this

question. Interior point methods basically do not follow a path along the extreme

points of the polyhedron, but go through the interior of it. If a single optimal so-

lution (which is an extreme point) exists, the algorithm approximates this solution,

and a ﬁnal rounding step will result in the optimal solution. If multiple optimal

solutions exist, an interior point algorithm might approximate any convex combina-

tion of the extreme optimal solutions, and the resulting optimal solution might be

different from the optimal extreme points. We refer to [88] for a detailed discussion.

18 A. M. C. A. Koster, X. Mu

noz

Dynamic Column Generation

Some formulations of optimization problems as (integer) linear programs require a

very large number of variables, typically exponential in the problem input size. An

example is the set of variables representing all possible paths between two nodes in

a network; see Section 1.5.2.2. In such cases, it is irrational and often impossible to

generate and store all variables in the optimization software. The implicit handling

of such very large sets of variables is known as dynamic column generation. Instead

of all variables, only a small subset of the variables is generated in the beginning, and

the remaining variables are not considered in the ﬁrst instance. For the initial subset

of variables the reduced linear program known as the master program is solved to

optimality. Next, all remaining variables (implicitly set to 0) are checked for the

capability of potentially improving the solution by adding them to the small set of

explicitly handled variables. If some candidates are found, they are added to the

linear program, and this is solved again. The procedure is repeated until no further

candidates are found. In this case, the optimal solution is found without dealing with

all variables explicitly. The problem of ﬁnding candidate variables to be included in

the master program is known as the pricing problem and usually can be formulated

as a linear or integer linear program.

1.4.1.3 Solving Mixed-Integer Linear Programming Problems

An integer linear program (ILP) is an optimization problem satisfying the following

conditions

• the objective is a linear function of the variables

• all constraints are linear in the variables

• the variables can take only integer values (i.e. ∈ Z)

By this deﬁnition, an ILP can be written w. l. o. g. in its standard maximization form

⎧

⎨

⎩

max c

s.t. Ax = b

x ∈Z

(1.5)

with matrix A ∈ Q

m×n

, a right-hand side b ∈Q

, and arbitrary objective values c ∈

.Amixed-integer program (MIP) generalizes the above deﬁnition by requiring

only a subset of the variables to be integer and allowing the remaining ones to take

continuous values. The methods to solve ILPs and MIPs are basically the same, and

therefore not further distinguished in this chapter.

For the purpose of our exposition, it is more convenient to rewrite the formula-

tion (1.5) to a system of linear inequalities:

⎧

⎨

⎩

max c

s.t. Ax ≤b

x ∈Z

(1.6)

1 Graphs and Algorithms in Communication Networks on Seven League Boots 19

The linear relaxation of (1.6) is obtained by replacing the integrality constraints

by nonnegativity constraints. Figure 1.5 illustrates for a given system of linear in-

equalities the integer-feasible solutions (i.e., the grid of points) as well as the LP

relaxation (the polytope).

objective

solution

Fig. 1.5 Integer-feasible solutions and the LP relaxation for a system of linear inequalities

Branch-and-Bound

The most common method to solve ILPs is branch-and-bound (B&B). In a B&B

algorithm, the linear programming relaxation of (1.6) is solved multiple times, each

time with other bounds on the variables. Let z be the optimal solution value of (1.6).

The algorithm starts with solving the LP relaxation, returning a solution ˆx. Since the

LP relaxation contains all integer-feasible points (cf. Figure 1.5), the value of the

LP relaxation z

= c

ˆx is an upper bound on z.Ifˆx ∈ Z

, the solution is also valid

for (1.6), and hence we found an optimal solution. If ˆx ∈ Z

, there is at least one

fractional variable ˆx

. In an optimal solution, either x

≤ˆx

 or x

≥ˆx

. There-

fore, we perform branching on x

: we replace the LP relaxation with two new sub-

problems, one with the variable bound x

≤ˆx

 and one with the variable bound

≥ˆx

; see Figure 1.6 for illustration.

solution

objective

new LP

Fig. 1.6 Branching on a fractional variable: two subproblems provide new optimal LP solutions

20 A. M. C. A. Koster, X. Mu

noz

Every optimal solution of (1.6) is in either of the new polyhedra, and thus

z = max{z

} where z

and z

are the optimal (integer) solution values of the sub-

problems respectively. Moreover, z ≤max{z

}≤z

bounds the optimal value

from above, where z

and z

are the values of the corresponding LP relaxations.

In case the LP relaxation of the ﬁrst (second) subproblem is integral, z ≥ z

= z

(z ≥ z

= z

), and we can bound the optimal value from below. The procedure

can be repeated recursively for the subproblems as long as the two bounds are not

equal. For further details, we refer to [82, 92] or to any one of the many textbooks

in Operations Research.

Polyhedral Combinatorics

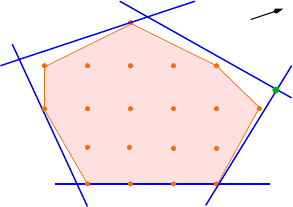
Polyhedral combinatorics is the study of the structure of the polytope (polyhedron)

described by the integer solutions of (1.6). Given the set of integer solutions, we

can deﬁne P as the convex hull of these points; see Figure 1.7. If we can derive

a system of linear inequalities describing this polytope, (1.6) can be solved by the

Simplex Algorithm (or interior point methods, possibly with a slight permutation of

the objective) since every extreme point is integral by deﬁnition.

objective

solution

Fig. 1.7 The convex hull of integer solutions can be described by a system of linear inequalities

An inequality ax ≤a

is called valid if ax

∗

≤a

for all x

∗

∈P.LetF(a,a

)={x ∈

P : ax = a

} be the set of polytope points that satisfy the valid inequality with equal-

ity. If F = /0 it describes a face of P. A valid inequality is facet-deﬁning if F(a,a

)

is maximal, i.e., there is no other valid inequality dx ≤ d

with F(a, a

) ⊂ F(d, d

Stated otherwise, the intersection of the polytope and a facet-deﬁning valid inequal-

ity forms a face of the polytope of highest possible dimension (without having

F = P); see Figure 1.8.

A valid inequality is also called a cutting plane as it might cut off a fractional so-

lution from the integer solutions. A cutting plane algorithm follows this procedure.

First, the LP relaxation is solved. Next, if the LP solution ˆx is not integral, there

exists a valid inequality ax ≤ a

that is violated by ˆx, i.e., aˆx > a

. This inequality is

added to the system of inequalities deﬁning the LP relaxation, and the enlarged LP