Koster A., Munoz X. Graphs and Algorithms in Communication Networks
Подождите немного. Документ загружается.

1 Graphs and Algorithms in Communication Networks on Seven League Boots 41
1.5.4.2 General Network Planning Problem (GNPP)
The network is represented as a directed graph G
net
=(N,L) with the set N of nodes
and the set L of the possible links. The demands are also represented by a directed
graph G
dem
=(N,D) over the same node set N and a function dem : D → R
+
. Each
demand is represented by an edge d ∈ D, where the tail and the head of d show
the source and the target of the demands, respectively, while dem(d) is the amount
of the demand. Moreover, we are given a monotone increasing load-dependent cost
function on each link, denoted by cost : L×R
+
→ R
+
, so the cost of establishing a
link with capacity c (or upgrading to capacity c)iscost(,c).
Then, the task is to assign a route p
d
to each demand d in such a way that the
obtained configuration minimizes the total cost
∑
∈L
cost(,traffic()), where traffic()=
∑
d:∈p
d
dem(d). (1.17)
This definition models several usual network optimization problems. Some ex-
amples are shown below.
Routing Configuration
Let us assume that we are given a network with given link capacities cap() and
the set of demands we want to carry over this network while keeping the capacity
constraints or minimizing the total overload. This problem can be modeled by the
framework above by defining the following cost function.
cost(,t)=max(0,t −cap()) (1.18)
If we want to minimize the number of overloaded links instead of the total overload,
we can use the following
cost(,t)=
0, if t ≤ cap()
0, if t > cap()
(1.19)
Network Design
This case is a green-field network planning problem: we want to plan a new network
carrying our traffic and we want to minimize the installation costs. Then L will
consist of all possible links, while cost(,t) is defined to be the cost of installing
a link of capacity t between the source and the destination of . As we can choose
only from some fixed capacity equipment, the cost will be a step function for each
possible link .
42 A. M. C. A. Koster, X. Mu
˜
noz
Network Extension
This case is similar to the previous one, but now we have some existing links, which
can be used with no extra installation cost. In this scenario, the cost cost(,t) of an
existing link with capacity cap() is 0 for all t ≤ cap().
1.5.4.3 Solution Methods
Local Search
The following simple observation plays a central role in solving GNPP.
Claim. Let us assume that we have fixed a route for all but one demand, i.e., we
have fixed p
d
for all d ∈ D \d
. Then the optimal route for the last demand d
can
be found by searching for a shortest path (using Dijkstra’s algorithm) according to
the following auxiliary length function.
len()=cost(,traffic
d
()+dem(d
)) −cost(,traffic
d
()), (1.20)
where
traffic
d
()=
∑
d:d=d
∧∈p
d
dem(d). (1.21)
Using the claim above, a simple heuristic can be given as follows. We start with
an arbitrary solution; then in each iteration we remove a route from the configuration
and replace it by the locally best alternative. We repeat this process until no more
improving change is possible. We refer this as the Local Search (LS) method.
It is easy to see that this method finds the theoretically optimal solution if the cost
function is linear in the second variable. However, it works poorly for the two most
typical cost functions, the concave and the staged costs, especially for the latter one.
Cost Function Smoothing (CFS) Algorithm
The main weakness of the LS scheme is that it considers the cost function as a black
box and queries its values only for the current traffic on the links. So, it does not
take into consideration how much traffic can be still allocated on the link before we
actually reach the next stage in the cost function, or how much should be deallocated
for realizing real cost decrement.
A solution proposed by [71] is to smooth the actual cost function by convolving it
with a “Gauss-like” function. This smoothed cost function cost
δ
(,t) should be pa-
rameterized in such a way that for large
δ
values it provides a very smooth function
(close to linear for practical t values) and it approaches cost(,t) as
δ
approaches 0
(see Figure 1.10).
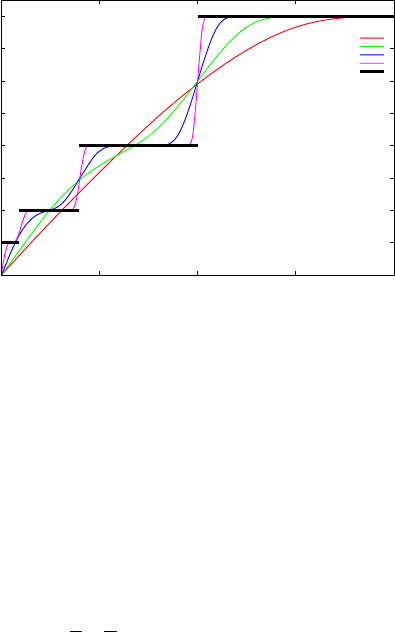
1 Graphs and Algorithms in Communication Networks on Seven League Boots 43
Then, the CFS algorithm is the same as LS with the exception that we use
cost
δ
(,t) instead of the original cost function. We start with a large
δ
value and
decrease it exponentially during the execution of the algorithm.
0
1
2
3
4
5
6
7
8
0 5 10 15 20
delta=10
delta=5
delta=2
delta=.5
original
Fig. 1.10 cost
δ
(,t) with different
δ
values
A concrete example for such a smoothing is the following (this is a refined ver-
sion of what is given in [71]).
cost
δ
(,t)=(cost
(,·) ∗h
δ
(·))(t)=
∞
−∞
cost
(,
ξ
)h
δ
(t −
ξ
)d
ξ
, (1.22)
where
cost
(,t)=
cost(,t) if t ≥0,
−cost(,−t) otherwise,
(1.23)
h
δ
(t)=
1
δ
h(
t
δ
), (1.24)
and
h(t)=
⎧
⎨
⎩
1−2t
2
for |t|≤1/2
2(|t|−1)
2
for 1/2 ≤|t|≤1
0for1≤|t|.
(1.25)
The symmetric definition of the cost function in (1.23) ensures that cost
δ
(,0)=0
holds for all
δ
. The advantage of smoothing function (1.25) is that the convolution
integral is a polynomial for constant or linear segments of the cost functions; thus it
is fast to evaluate for staged or piecewise linear cost functions.
44 A. M. C. A. Koster, X. Mu
˜
noz
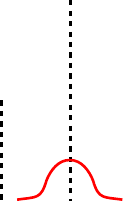
Randomized Cost Smoothing (RCFS) Algorithm
This approach is somewhat similar to the Cost Function smoothing, but instead of
modifying the cost function, we apply a random “uncertainty” when querying its
values. Namely, we change Equation (1.20) to the following.
len()=cost(,traffic
d
()+dem(d
)+R
δ
) −cost(,traffic
d
()), (1.26)
where R
δ
is a certain random variable of standard deviation
δ
. Natural choices for
R
δ
include the Gaussian distribution N(0,
δ
2
) and the exponential distribution. If R
δ
can also take negative values, then len
()=max(0,len()) should be used in order
to avoid negative lengths. Note that Dijkstra’s algorithm reads the length of each
link only once, so this gives a consistent length function in each iteration.
d’
tr (l)
d’
tr (l)+dem(d)
Fig. 1.11 Randomized smoothing of cost(,t)
Note that the expected value of cost(,t +R
δ
) is the same as cost(,t) smoothed
or convolved by the probabilistic distribution function of the random variable R
δ
;
thus this approach indeed performs a “randomized smoothing.” On the other hand,
an expected advantage of this scheme is that similarly to other metaheuristics such as
Simulated Annealing or the Evolutionary Algorithms, the randomness may provide
higher freedom for the algorithms when choosing replacement of a route; thus it
may have a higher chance of avoiding the local optima that are far from the global
optimum.
1.5.4.4 Evaluation
Here, we demonstrate the behavior of the algorithms on a single but representa-
tive network topology. The test network (see Figure 1.12) is a two-connected pla-
nar graph consisting of 50 nodes and 84 bidirectional links. It was generated by
lgfgen, a random graph generator of LEMON [70].
The cost function is a step function, and it is also linearly proportional to the
physical length of the link, i.e,
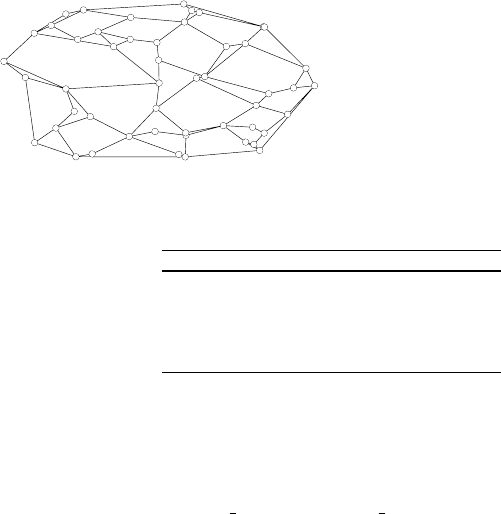
1 Graphs and Algorithms in Communication Networks on Seven League Boots 45
Fig. 1.12 Test network example with 50 nodes and 84 links
Table 1.1 Cost obtained by the different algorithms
Homogeneous demands Big trunks
SHORTEST 91101 89575
LS 83371 72601
CFS 59890 56158
RCFS/Gauss 86722 69444
RCFS/Exp 63342 52104
cost(,t)=length()step fn(t), where step fn(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎩
0fort = 0,
1for0< t ≤ 1,
2for1< t ≤ 4,
4for4< t ≤ 10,
8 for 10 < t ≤ 100,
M for 100 < t.
Two different types of demand matrices were chosen for the tests.
• Homogeneous demands. In this scenario, we have a homogeneous traffic matrix,
i.e., we have the same amount of traffic between any pair of nodes.
• Big trunks. In this scenario only 245 (out of the 2450 possible) random pairs
of nodes was chosen as traffic sources and destinations but the demands are 10
times larger than in the previous case.
We ran LS, CFS, and RCFS methods on these examples, and we also computed the
cost of the simple shortest path routing (SHORTEST) as a reference. In the case of
RCFS, both Gaussian and exponential randomization have been tested. The costs of
the obtained solutions are presented in Table 1.1.
The algorithms were implemented in C++, heavily based on the LEMON li-
brary [70]. The tests were made on a laptop equipped with a 2 GHz Centrino Duo
processor and running the Linux (OpenSuse 10.2) operating system.
The running times of SHORTEST (less than 0.1 second) and LS (a few seconds)
are obviously much less than those of CFS and RCFS. Actually, the running times
of these algorithms depend on the number of their iterations. Thus, the number of
iterations was chosen in such a way that the resulting running time was around
40 seconds. The other parameters were tuned to provide the best results.
46 A. M. C. A. Koster, X. Mu
˜
noz
It is worth mentioning that RCFS completes around 2,000,000 iterations within
40 seconds while CFS completes only around 400,000 within the same time. This
is because the cost function calculation must be performed at each iteration of the
algorithms; thus, it turns out to be the most resource-consuming part of the algo-
rithms. Therefore, the easier calculation of the randomized cost function makes the
running time of an iteration of RCFS much smaller than that of CFS.
Considering the two versions of RCFS, the results show that the Gaussian version
performed quite poorly. In fact, in the case of homogeneous demands, this version
is even outperformed by the simple LS method. The possible explanation of the
better performance of the exponential-distribution-based version is that this cost
randomization can be interpreted as a stochastic prediction of the amount of traffic
that will be allocated on the link in the subsequent iterations.
Comparing CFS and RCFS, we obtained that for a homogeneous traffic matrix
the winner is CFS, while for uneven traffic with big trunks RCFS outperforms CFS.
The reason for this is that for a homogeneous traffic matrix, the traffic can be almost
continuously distributed on the links and the cost function smoothing seems to per-
form really well. On the other hand, if there are fewer but larger unsplittable traffic
flows, the problem becomes a combinatorial packing problem, and in this case the
RCFS method is able to scan a larger portion of the search space.
1.5.5 Wireless Networking
In wireless networking, two classical combinatorial optimization problems have re-
ceived a lot of attention. We first discuss the frequency assignment problem in wire-
less networks which is closely related to the vertex coloring problem. Second, the
maximum coverage problem is considered, a problem whose basic version can be
modeled as a set covering problem.
1.5.5.1 Assignment of Frequencies
The frequency assignment problem (FAP), or channel assignment problem, plays
an important role in all wireless networks that use the frequency division multiple
access (FDMA) technology, the most prominent example being the second genera-
tion of cellular networks based on the GSM technology. Other applications include
satellite communication, TV broadcasting, military wireless networks, WLANs, and
Orthogonal Frequency Division Multiplexing (OFDM) in future wireless networks.
Due to this wide variety of applications, there does not exist a single frequency
assignment problem, but many variations. The problem was first mentioned in the
1960s [75] when individual frequencies in the radio spectrum were licensed (and
charged) by the authorities, and operators of the first cellular phone networks could
financially benefit from intelligent frequency planning. Later, frequencies were li-
censed in blocks and the objective of the operators changed to minimize the dif-
1 Graphs and Algorithms in Communication Networks on Seven League Boots 47
ference between the highest and lowest frequency to be used. In the 1990s most
frequencies were licensed and the popularity of mobile communication forced op-
erators to increase the number of antennae, significantly causing high interfer-
ence levels whenever the frequency planning was not done carefully. Accordingly
the objective changed to the minimization of interference or the maximization of
interference-free operated antennae.
All these different objectives have been addressed in a vast number of scientific
publications. For an overview on the state of the art of frequency assignment we
refer to Aardal et al. [3] and the FAP website [44]. In this section, we will restrict
ourselves to the basic modeling of the frequency assignment problem and its relation
with the vertex coloring problem in undirected graphs.
Frequency Assignment and Vertex Coloring
All variations of frequency assignment have two features in common.
1. A set of wireless transmitters must be assigned frequencies. For each transmitter
there is a set of available frequencies given.
2. The frequencies assigned to two transmitters may incur interference of one an-
other, resulting in quality loss of the signal. Two conditions must be fulfilled in
order to have interference of two signals:
• The two frequencies must be close on the electromagnetic band. Harmonics
may also interfere due to the Doppler effect, but the parts of the electromag-
netic band that are generally selected prevent this type of interference.
• Connections must be geographically close to each other, so that interfering
signals are powerful enough to disturb the quality of a signal.
Usually, data on the level of interference is provided for every quadruple of two
transmitters and two frequencies.
This rather general description is complemented by an objective to be optimized.
The problem can be modeled as a graph-theoretical problem by defining an undi-
rected interference graph G =(V,E) describing the interference relations. To sim-
plify the presentation we assume in this section that no transmitters are colocated, as
is usually the case in cellular phone networks (the description can be easily adapted
to such situations; see, for example, [41]). The set V now represents all transmitters.
The planner can choose a threshold value representing an acceptable level of inter-
ference. An edge {i, j}∈E exists if and only if there exists a frequency pair ( f , g)
such that the interference level for the quadruple (i, f , j,g) exceeds the threshold.
In the most simplified case we only consider so-called co-channel interference,
i.e., an edge exists if and only if the interference level exceeds the threshold for as-
signing the same frequency to both transmitters. We further assume that the set of
frequencies is equal for all transmitters and the objective is to minimize the num-
ber of frequencies under the condition that all interference levels remain below the
threshold. In this case, FAP reduces to the well-known vertex coloring problem.In
48 A. M. C. A. Koster, X. Mu
˜
noz
the vertex coloring problem, we have to color the vertices of a graph G =(V,E) such
that no two adjacent vertices get the same color. The chromatic number
χ
(G) is the
minimum number of colors needed in a feasible coloring of G. It is not difficult to
see that in the above-described case the minimum number of frequencies needed
equals
χ
(G).
From an algorithmic point of view, this problem can be either treated as a deci-
sion problem or an optimization problem. If the number of frequencies is fixed, say
K, the planner has to answer the question: “Does there exist a solution without unac-
ceptable interference using at most K frequencies?” which is equivalent to solving
the K-C
OLORABILITY decision problem. This problem is not only NP-hard [66] but
also hard to approximate [14]. In the case where the number of frequencies is not
yet fixed but must be determined, the optimization version of K-C
OLORABILITY
has to be solved.
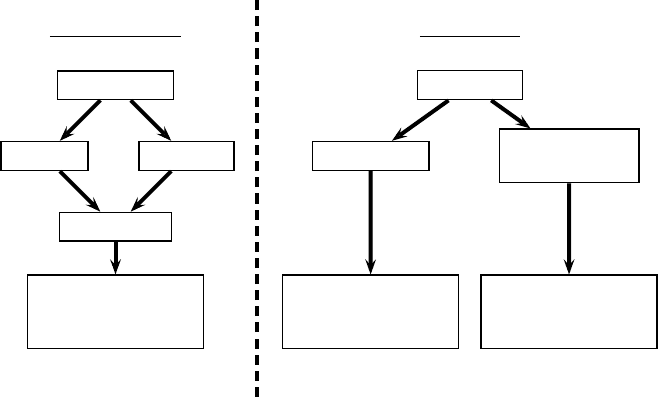
unlimited spectrum
vertex coloring
T-coloring list coloring
list T-coloring
Minimum Span
Frequency Assignment
(MS-FAP)
fixed spectrum
k-colorability
min-k-partition
max-k-colorable
induced subgraph
Minimum Interference
Frequency Assignment
(MI-FAP)
Minimum Blocking
Frequency Assignment
(MB-FAP)
Fig. 1.13 Classification of vertex coloring and frequency assignment problems
This differentiation between choice of frequencies (unlimited spectrum) and
fixed frequencies (predetermined spectrum) also holds for more realistic frequency
assignment problems; see Figure 1.13. If we include the sets of available frequen-
cies to the vertex coloring problem, a list coloring problem has to be solved, whereas
the inclusion of interference levels between nonidentical frequencies results in a T-
coloring problem. Both these variants on the vertex coloring problem have origi-
nally been studied in the context of frequency assignment, providing perfect show-
cases of the interaction between discrete mathematics and applications.
The combination of T- and list coloring is known as List-T-coloring. If not the
number of frequencies but the difference between highest and lowest frequency has
to be minimized, the problem is known as the minimum span FAP.

1 Graphs and Algorithms in Communication Networks on Seven League Boots 49
In the case of a fixed spectrum, K-COLORABILITY is generalized in two ways
in case the problem is infeasible. If the planner needs to assign a frequency to
each transmitter, some unacceptable interference has to be permitted. Otherwise,
the planner might consider leaving some transmitters unassigned to avoid unaccept-
able levels of interference. If only co-channel interference is considered, the first
case is known as the minimum K-partition problem: We associate a value c
co
e
∈ Q
+
with all edges e ∈ E. The minimum K-partition problem now consists of a partition
of the vertices in K subsets S
1
,...,S
K
such that the sum over all subsets of the to-
tal weight c
co
e
of the edges in G[S
i
] is minimized. Stated otherwise, all vertices in
a subset are assigned the same frequency, and so the interference incurred by this
assignment is given by the sum of the weights c
co
ij
for all i, j ∈ S
i
. A solution with
total weight 0 exists if and only if the graph is K-colorable. See [42] for a solution
approach using semidefinite programming.
The second case is known as k-colorable induced subgraph. In this problem we
have to color as many vertices as possible with K colors. A solution where all ver-
tices are colored implies that the graph is K-colorable, whereas non-K-colorable
graphs have at least one vertex uncolored in any K-colorable induced subgraph so-
lution.
The inclusion of potential interference between nonidentical frequencies for
transmitter pairs results in the study of the so-called minimum blocking FAP. In-
clusion of the same information in the minimum K-partition problem results in the
minimum interference FAP.
Frequency Assignment in GSM Networks
We conclude the discussion of FAP with the formulation as integer linear program of
the minimum interference problem with co- and adjacent-channel interference,asit
occurs frequently in GSM networks.
2
Usually an operator of a GSM cellular phone
network has acquired the right to use a certain spectrum of frequencies [ f
min
, f
max
] in
a particular geographical region, e.g., a country. The frequency band is—depending
on the technology utilized—partitioned into a set of channels, all with the same
bandwidth
Δ
. The available channels are here denoted by F = {1,2,...,N}, where
N =(f
max
− f
min
)/
Δ
. A transmitter pair is exposed to adjacent-channel interference
if the assigned frequencies are consecutive numbers in the spectrum.
In GSM networks, communication between mobile and base station (up-link)
as well as between base station and mobile (down-link) must be established. To
simplify the management of these networks, two separate, but paired, spectrums of
frequencies are licensed, one for up-link and one for down-link. For FAP one can re-
strict assigning down-link frequencies to the base stations, as the paired frequencies
can then be used for up-link communication.
We associate with the edges of the interference graph G =(V, E) two values
c
co
ij
,c
ad
ij
∈ Q
+
denoting the level of co- and adjacent-channel interference between
2
Some details are ignored; see, for example, [43] for a more detailed discussion
50 A. M. C. A. Koster, X. Mu
˜
noz
the vertices. For ease of notation we introduce two subsets:
E
co
= {ij∈ E | c
co
(
ij) > 0}, and
E
ad
= {ij∈ E | c
ad
(
ij) > 0}.
Given a subset F
i
⊆ F for all i ∈V, the formulation uses binary variables x
if
, indi-
cating whether frequency f ∈ F
i
is assigned to vertex i ∈ V. We further introduce
variables z
co
ij
and z
ad
ij
to denote violation of the co-channel and adjacent-channel
constraints, respectively. Then, the integer linear program reads
min
∑
ij∈E
co
c
co
ij
z
co
ij
+
∑
ij∈E
ad
c
ad
ij
z
ad
ij
(1.27a)
s.t.
∑
f ∈F
i
x
if
= 1 ∀i ∈V (1.27b)
x
if
+ x
jf
−z
co
ij
≤ 1 ∀ij∈ E
co
, f ∈ F
i
∩F
j
(1.27c)
x
if
+ x
jg
−z
ad
ij
≤ 1 ∀ij∈ E
ad
, f ∈ F
i
,g ∈F
j
: |f −g|= 1
(1.27d)
x
if
,z
co
ij
,z
ad
ij
∈{0,1} (1.27e)
If ij ∈ E
co
and frequency f can be assigned to both vertices, constraint (1.27c)
assures that such a mutual assignment incurs a penalty of c
co
ij
. Similarly, con-
straint (1.27d) guarantees that the adjacent-channel interference is comprised of the
objective if ij∈E
ad
and the frequencies f and g differ by 1.
A major drawback of the above formulation is the difficulty to solve these
coloring-like integer linear programs to optimality. A wide range of different ap-
proaches have therefore been proposed to compute close-to-optimal solutions and/or
lower bounds on the minimum total interference; see [3] for a survey. In Chapter 11
a similar frequency assignment model is studied in more detail for the case of wire-
less local area networks (WLANs). Due to the limited number of frequencies the
drawbacks of the above formulation have less impact in this case.
Figure 1.14 shows an example of a carrier network, where the so-called DSATUR
heuristic [24] followed by a very simple local search heuristic (1-opt) is ap-
plied. This procedure improved the solution provided by a network operator by
96% [23, 43]. In the plots, transmitters are represented by dots in the Euclidean
plane according to their geographical coordinates. Two transmitters are connected
by a colored line if the assignment of frequencies results in interference. If the line
is drawn in a pale color, then the interference is small. With increasing interference,
the color of the line turns black.
1.5.5.2 Maximization of Network Coverage
Besides the frequencies on which the antennae operate, the locations of the antennae
and their configuration play an important role in the performance of the network.
In fact, these decisions are typically taken before the frequencies are considered.
