Koster A., Munoz X. Graphs and Algorithms in Communication Networks

Подождите немного. Документ загружается.

Chapter 11

Mathematical Optimization Models for WLAN

Planning

Sandro Bosio, Andreas Eisenbl

atter, Hans-Florian Geerdes, Iana Siomina, and Di

Yuan

Abstract Wireless Local Area Networks (WLANs) based on the I

EEE 802.11 stan-

dard family are used widely for wireless broadband Internet access. The perfor-

mance aspects of WLANs range from deployment cost, coverage, capacity, interfer-

ence, and data throughput to efﬁciency of radio resource utilization. In this chapter,

we summarize some recent advances in applying mathematical optimization models

for solving planning problems arising in placing access points (APs) and assigning

channels in WLANs. For AP location, we present an optimization model aimed at

maximizing the average user throughput. For channel assignment, we present two

modeling approaches that use different performance metrics. We also discuss inte-

grated models for joint optimization of AP location and channel assignment. We

report computational experiments with real-life data, and show the advantages of

mathematical optimization in WLAN planning.

Sandro Bosio

Institut f

ur Mathematische Optimierung, Otto-von-Guericke Universit

at, D-39106 Magdeburg,

Germany, e-mail: bosio@mail.math.uni-magdeburg.de

Andreas Eisenbl

atter

atesio GmbH, Sophie-Taeuber-Arp-Weg 27, D-12205 Berlin, Germany, e-mail:

eisenblaetter@atesio.de,and

Zuse Institute Berlin (ZIB), Takustr. 7, D-14195 Berlin, Germany, e-mail:

eisenblaetter@zib.de

Hans-Florian Geerdes

Zuse Institute Berlin (ZIB), Takustr. 7, D-14195 Berlin, Germany

Iana Siomina

Ericsson Research, Ericsson AB, Isafjordsgatan 14E, SE-164 80, Stockholm, Sweden, e-mail:

iana.siomina@ericsson.com

Di Yuan

Department of Science and Technology, Link

oping University, SE-601 74, Norrk

oping, Sweden,

e-mail: diyua@itn.liu.se

A.M.C.A. Koster, X. Mu

noz (eds.), Graphs and Algorithms in Communication 283

Networks, Texts in Theoretical Computer Science. An EATCS Series,

DOI 10.1007/978-3-642-02250-0

11,

 Springer-Verlag Berlin Heidelberg 2010

284 S. Bosio et al.

Key words: integer linear programming, performance, optimization, wireless local

area networks, WLAN

11.1 Introduction

WLAN (Wireless Local Area Network, also WiFi) is a technology for providing

wireless broadband Internet access. Due to their low cost and ease of use, WLANs

are widely deployed. The network layout and its conﬁguration determine the per-

formance of a WLAN; important performance indicators are deployment cost, cov-

erage, capacity, interference, data throughput, and efﬁciency of radio resource uti-

lization. At present, WLANs are often installed using rules of thumb; this calls for

quantitative and systematic methods that can outperform manual approaches. This

chapter presents mathematical optimization approaches to the problems of locating

access points (APs) and assigning a channel to each of them. We show how math-

ematical models can capture the essential features of the technology and provide

superior network designs.

Most aspects of WLAN optimization resemble problems studied in mobile cel-

lular network planning. The AP positioning problem is akin to base station posi-

tioning and coverage planning in cellular networks. Due to the smaller coverage

area of WLANs, however, the number of installed APs is smaller, and the signal

propagation characteristics are different. Moreover, WLANs are mainly intended

for providing broadband access to users that are rather stationary. Channel assign-

ment for minimizing interference is needed in WLAN just as, for instance, in GSM

(see Section 1.5.5.1). The number of channels is, however, much smaller, and access

to the medium is controlled by a contention mechanism on each channel. The im-

pact of this mechanism on network performance is paramount, and requires tailored

modeling approaches.

We present several optimization models for the planning phase of deploying

WLAN. The models can use both measurements and prediction-based data. As data

are collected prior to solving the models, optimization can be performed using cen-

tralized computation. We optimize AP location using a facility location model in

which the average single-user throughput is maximized. Two modeling approaches

are considered for channel assignment: overlap graphs and contention sets. With

overlap graphs, each pair of APs is assigned a weight proportional to the area in

which the received signal strengths of the two APs are above some thresholds. Chan-

nel assignment has the objective of minimizing the total weighted overlap of APs

on the same and adjacent channels. Two integer-linear programming models for

minimum-overlap channel assignment are discussed in the chapter. For each user,

the contention set comprises all other users potentially contending for medium ac-

cess with the user. The modeling approach resulting from the concept uses a per-

formance metric, called network efﬁciency, that reﬂects the average probability of

successful access to the medium. Using contention sets, the goal is to maximize

the network efﬁciency metric. Because the contention sets carry information on

11 Mathematical Optimization Models for WLAN Planning 285

medium contention of each individual user, they model WLAN medium access

more accurately than AP overlap, which represents medium contention through an

aggregated view. On the other hand, maximum-efﬁciency channel assignment using

contention sets leads to complex models. In the chapter, we present a hyperbolic in-

teger programming model for maximum-efﬁciency channel assignment, and derive

a linearization based on the enumeration of contention sets.

In addition to models for performing AP location and channel assignment sepa-

rately, we present optimization models that integrate AP location with channel as-

signment. Integrating AP location with minimum-overlap channel assignment leads

to an objective function representing a trade-off between overlap minimization and

throughput maximization. For the modeling approach using contention sets, the ob-

jective of maximizing efﬁciency can be used for joint AP location and channel as-

signment.

We report computational experiments for a real-life WLAN planning instance,

where the input parameters are based on real throughput measurements and detailed

signal-propagation modeling. The input data include a set of potential AP locations

in an ofﬁce building, a set of available channels, a set of test points representing ex-

pected user locations, and signal propagation data between candidate AP locations

and test points. The strengths and the capabilities of both the sequential approaches

and of the integrated model are assessed. In our experiments, the WLAN designs ob-

tained from the optimization models considerably outperform the manual planning

solution which has been deployed in the network.

The remainder of the chapter is organized as follows. Some technical background

of WLANs is provided in Section 11.2; the related work on WLAN planning is re-

viewed in Section 11.3. Mathematical notation and deﬁnitions used in the chapter

are introduced in Section 11.4. Section 11.5 discusses the optimization of AP loca-

tions. The models for minimum-overlap channel assignment are presented in Sec-

tion 11.6. The concept of contention set and the resulting models are presented in

Section 11.7. The integration of AP location and channel assignment is then dis-

cussed in Section 11.8. Computational experiments are presented in Section 11.9.

Finally, Section 11.10 gives some conclusions and an outlook on future develop-

ments.

11.2 Technical Background

The WLAN technology is deﬁned in the IEEE 802.11 standard [16], specifying a

number of possible physical-layer implementations as well as many networking as-

pects. At present, WLANs using I

EEE 802.11b and the more recent IEEE 802.11g

are the most popular. (These former amendments have now been joined in the lat-

est standard.) They use different physical-layer implementations on the same fre-

quency band at 2.4 GHz. I

EEE 802.11g is backward-compatible, so that hardware

implementing the two standards can interoperate.

286 S. Bosio et al.

11.2.1 Physical Layer

WLANs employ rate adaptation to utilize the radio channel efﬁciently. According

to the received signal strength, the raw data rate on a link is selected from a discrete

set ranging up to 54 Mbit/s (11 Mbit/s for I

EEE 802.11b). Due to protocol overhead,

however, the net data rate is much lower (see Figure 11.4).

Both the I

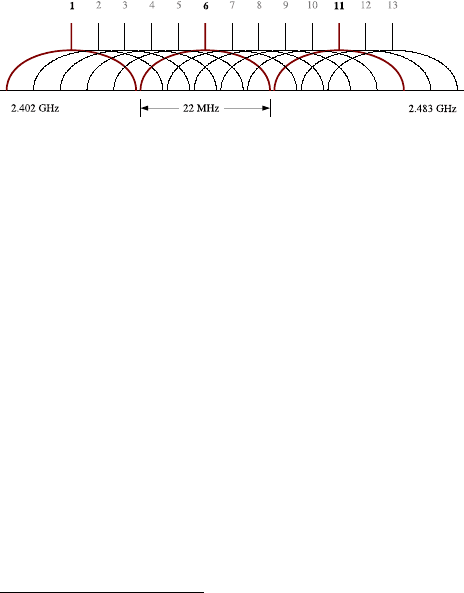
EEE 802.11b and 802.11g standards divide the 2.4 GHz spectrum

into 13 channels.

Two neighboring channels are separated by 5 MHz, as shown

in Figure 11.1. Channels with at least 24 MHz separation are considered to be

non-overlapping. Otherwise, they are called adjacent or overlapping channels. The

spectrum available to WLAN provides at most three non-overlapping channels (for

example, channels 1, 6, and 11; see Figure 11.1). Since the 2.4 GHz spectrum is

unlicensed, a WLAN may also be subject to the interference of external radiation

sources (e.g., other WLANs, microwave ovens, cordless telephones).

Fig. 11.1 Channels speciﬁed by the IEEE 802.11b/g standards

11.2.2 Architecture

A station is a device containing an IEEE 802.11 network interface card (NIC). A

WLAN connects stations either in ad hoc mode or in infrastructure mode. A basic

service set (BSS) is a set of stations that can communicate either directly or through

some other station. If stations are able to communicate directly, we speak of an in-

dependent basic service set (IBSS). If a self-contained network is thus formed, this

is referred to the ad hoc mode of WLAN. In graph terminology, the stations of a

WLAN in ad hoc mode form a clique, assuming that no station has been conﬁg-

ured to perform network layer routing for other stations. In the infrastructure mode,

the stations in a BSS communicate through an access point (AP), which is itself a

station. In the rest of this section, we will refer to user stations simply as users,or

mobile terminals (MTs).

Channel availability varies by country due to radio spectrum regulation. The 13 channels are

typically available in the European Telecommunications Standards Institute (ETSI) regulatory do-

main. One additional I

EEE 802.11b channel is available in Japan. In North America, the Federal

Communications Commission (FCC) and Industry Canada (IC) restrict the spectrum usage to 11

of the 13 channels.

11 Mathematical Optimization Models for WLAN Planning 287

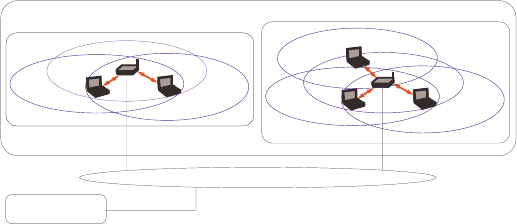
In the infrastructure mode, several BSSs are typically connected to a wired Ether-

net backbone, called the distribution system (DS). The DS enables mobility support

and seamless integration of multiple BSSs. BSSs connected via the DS form an ex-

tended service set (ESS) of a WLAN; see Figure 11.2. ESSs are used for broadband

Internet access, and are the focus of this chapter. Every user accesses the DS through

one AP of the ESS, with which the user is said to be associated. To announce its

presence, an AP periodically broadcasts special messages, called beacon frames,

on the frequency channel used by the AP. A user station seeks beacon frames on

all WLAN channels, and selects one AP for association. The 802.11 standard does

not specify an algorithm for selecting which of the available APs to associate with.

Typically, the station chooses the AP from which the beacon frame is received with

the best signal strength. By this choice, the station maximizes the expected data rate

(see Section 11.4). Some research has been conducted on alternative variants [3, 24].

The frequency channel used by the AP is inherited by all its associated users.

AP1

MT1

MT2

AP2

MT3

MT4

MT5

IEEE 802.x LAN

ESS

BSS1

BSS2

Fig. 11.2 Infrastructure mode of WLAN.

11.2.3 Medium Access Control

Unlike cellular networks (e.g., GSM or UMTS) where users obtain a dedicated re-

source in form of frequency, time slot, or channelization code, WLAN applies ran-

domized medium access, and uses a medium access control (MAC) mechanism to

deal with collisions and medium contention. The MAC mechanism is used in both

downlink (AP to user station) and uplink (user station to AP) directions. A collision

occurs when the signals of two or more transmitting stations overlay at either of the

receiving stations. Medium contention occurs when two (or more) stations compete

for using the medium. Stations transmitting on non-overlapping channels will not

cause collision or medium contention.

The I

EEE 802.11 protocol deﬁnes two MAC mechanisms: the Distributed Coor-

dination Function (DCF) and the Point Coordination Function (PCF). PCF is cen-

tralized and can therefore, in theory, avoid collision and medium contention at the

288 S. Bosio et al.

cost of coordination overhead. Implementing PCF is, however, optional, and DCF

is wider spread, so we focus on DCF. In DCF, stations negotiate medium access

among themselves in a distributed and randomized access scheme using a Carrier

Sense Multiple Access/Collision Avoidance (CSMA/CA) protocol.

In CSMA, before initiating a transmission, a station ﬁrst senses the medium. If

a signal from another station is detected on the same frequency channel, the station

waits for the ongoing transmission to ﬁnish before transmitting. This mechanism

avoids some collisions, but unresolved cases remain: In the hidden terminal sce-

nario, illustrated in Figure 11.3(a), a terminal (MT1 in the ﬁgure) senses the carrier

idle and starts transmission concurrently with another one (MT2). Neither of them

will detect the other’s signal because they are outside the respective radio ranges.

The result is a collision at the AP. Another interesting interference scenario is the ex-

posed terminal scenario, represented in Figure 11.3(b): A user MT2 needs to trans-

mit to its associated access point AP2, but a second access point AP1, having MT2

within the radio range, is transmitting to some other user MT1. Even though the two

transmissions could in fact take place simultaneously without collision (as MT2 is

not within radio range of MT1, and AP2 is not within radio range of AP1), MT2 is

not allowed to start transmitting, because it is exposed to an ongoing transmission.

MT1

MT2

(a) Hidden terminal problem

MT1

MT2

AP1

AP2

(b) Exposed terminal problem

Fig. 11.3 The hidden terminal problem and the exposed terminal problem. Radio ranges are indi-

cated by dotted ovals

CA is used to further reduce the probability of collisions. A receiving station ac-

knowledges each successful transmission. The absence of acknowledgment triggers

a retransmission. To reduce the probability of repeated collision, CSMA/CA uses

an exponential backoff scheme: If a station wishing to transmit senses the channel

idle, it senses for an additional, short period of time (the Distributed Inter-Frame

Space, DIFS). If the channel gets busy during the DIFS, the station keeps sens-

ing the channel until it is idle for a DIFS, and then generates a random backoff

interval from a range called the contention window. The contention window size

is doubled after each unsuccessful attempt and reset after a successful transmis-

sion. The backoff counter is decremented as long as the channel is sensed idle,

frozen when the channel is busy, and reactivated (without resetting) when the chan-

nel is again idle for more than a DIFS. The transmission starts when the backoff

counter reaches zero. In addition to the two-way handshaking (transmission and

acknowledgment) technique, DCF deﬁnes an optional four-way handshaking tech-

nique known as CSMA/CA with Request to Send (RTS) and Clear to Send (CTS).

RTS and CTS are short packets used to reserve the channel prior to payload trans-

11 Mathematical Optimization Models for WLAN Planning 289

mission. The RTS/CTS packet exchange, referred to as virtual carrier sensing, is

advantageous because collisions virtually occur only for these small signaling pack-

ets, and the exposed terminal problem and the hidden terminal problem are resolved

(if all stations have the same radio range).

11.2.4 Planning Tasks and Performance Aspects

The main decisions in WLAN planning are AP location and channel assignment.

These decisions should be taken with the objective of obtaining good network per-

formances. We shall now elaborate on these points.

Determining AP locations is usually the ﬁrst step in a WLAN deployment pro-

cess. Locations should be chosen so that the resulting WLAN provides coverage to

the intended service area. This requires signal strength measurements and/or pre-

dictions of radio propagation. Coverage planning for large buildings with multiple

ﬂoors is more involved: An AP located on one ﬂoor of the building may provide sig-

nal coverage, but sometimes also interference, to adjacent ﬂoors of the same build-

ing, or even to other buildings [14, 15]. Potential interference from neighboring

WLANs has to be considered as well.

Distributed and online channel assignments are presently not implemented in

APs. A WLAN typically uses a static channel assignment, or each AP uses a simple

heuristic to select a channel when powered on. Typically, the heuristic searches for

the least congested channel or the channel with the least amount of interference. Us-

ing the three non-overlapping channels 1, 6, and 11 is encouraged [8], since stations

transmitting on non-overlapping channels do not cause collision or contend for the

medium. In this chapter we focus on the case where a static channel assignment is

determined during the planning.

From a user standpoint, the most important WLAN performance indicator is the

data throughput. Since the bandwidth of the DS is typically much higher than that

of the radio interface, the radio link is the performance-limiting point. The data

throughput on the radio link depends on the net throughput experienced by the user

when holding the medium (which we call single-user throughput), on the number

of users associated with the same AP and their activity, and on interference due

to users associated with other APs. The single-user throughput is essentially deter-

mined by the distance (attenuation) to the associated AP, and is easy to model. An

appropriate modeling of interference and contention, on the other hand, is the main

task in designing optimization approaches to WLAN planning. In this chapter, the

model for optimizing AP location (Section 11.5) focuses on the aspect of single-

user throughput. The model can be applied to both downlink and uplink directions.

For channel assignment, the ﬁrst modeling approach (Section 11.6) uses an overlap

graph to provide an aggregated view of interference and contention. This approach

does not require us to distinguish between downlink and uplink. The second ap-

proach (Section 11.7) models in detail medium contention for every individual user,

and the resulting model is suitable for addressing performance of the uplink.

290 S. Bosio et al.

11.3 Related Work

AP location has been occasionally studied separately [21, 32, 36], with the objective

of optimizing signal coverage and quality, and without referring to the CSMA/CA

mechanism. The WLAN channel assignment problem is related to GSM frequency

assignment problems [1, 2, 23], notably to the minimum-interference frequency as-

signment (see Section 1.5.5.1). For GSM, graph-coloring techniques are used [12];

the graph-coloring approach is applied to WLAN in static [29] and dynamic [31, 37]

settings. Some contributions [26] use a more accurate model of MAC level perfor-

mance for channel assignment. Some NP-hardness results are known [26, 29] for

the channel assignment problem.

In conjunction, channel assignment and AP location for WLAN have often

been treated sequentially [14, 39], in a multi-objective setting [17]. Search heuris-

tics are most popular for these problems. Custom algorithms have been developed

in [27, 30]. Integer programming methods are also used [25, 28, 40]. The channel

assignment is, however, typically treated as a feasibility problem constraining an es-

sentially coverage-driven approach. In this chapter, Sections 11.5, 11.6, and 11.8.1

are based on [11, 33, 34], while Sections 11.7 and 11.8.2 are based on previous

work on efﬁciency optimization in single- and multiple-frequency WLANs [4–6].

11.4 Notation and Deﬁnitions

Let us introduce some mathematical notation to be used in our models. The set of

candidate AP locations is denoted by A = {1,...,A}, and we denote by A

{(a,b) : a,b ∈ A ,a < b} the set of ordered pairs of APs in A . Given two distinct

APs a,b, exactly one of (a,b) and (b,a) is in A

. The maximum number of installed

APs is denoted by M. The service area is represented by a set of test points (TPs)

I = {1,...,I}, where each element i ∈ I represents a potential user location. In

the remainder, the size of an area is measured by the number of TPs it contains.

For each AP a ∈ A we deﬁne a serving range, so that TPs within the serving

range of an AP can be served by the AP. For every TP i ∈ I ,weuseA

to denote

the set of APs for which i is within the serving ranges. Representing the same in-

formation from the AP point of view, we denote by I

the set of TPs that can be

served (or covered) by AP a ∈ A .

For every station (AP or TP) we deﬁne a second signal range, commonly referred

to as carrier sense range. A station is within carrier sensing range from some other

station if they operate on the same frequency channel and if the former, perform-

ing carrier sensing while the latter is transmitting, senses the channel as idle. This

implies that stations within each other’s carrier sense range have to contend for the

medium. For APs, the carrier sense range is at least as large as the serving range.

As discussed in Section 11.2.4, one important WLAN performance metric is

the single-user throughput, deﬁned as the maximum achievable throughput when

11 Mathematical Optimization Models for WLAN Planning 291

a user communicates with its associated AP without contention. We denote by t

the single-user throughput of TP i when it is associated with AP a.

The set of available channels is denoted by C ⊆{1,...,13}, and the dis-

tance (in MHz) between two channels c

∈ C by |c

− c

|. We denote by

D = {|c

−c

| : c

∈ C ,|c

−c

| < 24 MHz} the set of channel distances be-

tween overlapping channels. For example, if only the non-overlapping channels are

allowed, C = {1,6,11} and D = {0}, while if all the channels can be used then

C = {1,...,13} and D = {0, 5,10,15, 20} (due to the 5 MHz channel separation).

For the sake of simplicity, we assume that C does not vary by AP.

When channel assignment is considered, the set of installed APs is denoted by

A ⊆A , and the set of its pairs by

⊆ A

. We assume that each TP i ∈ I asso-

ciates with the AP providing the highest single-user throughput t

= max

a∈

and we denote such an AP by ¯a(i).

At the physical layer, the value of t

(and t

) is dependent on the received signal

strength. At the radio interface, this throughput corresponds to one of the nominal

data rates deﬁned in I

EEE 802.11 standards. From an application standpoint, the

throughput should be deﬁned as the end-to-end data throughput, for which unreli-

able radio propagation, protocol behavior, and overhead at the link layer and above

are the constraining factors. In either case, the throughput as a function of received

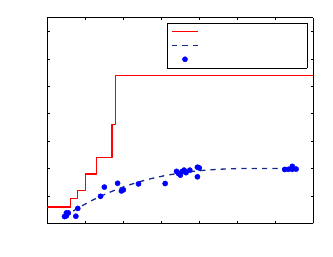
signal strength can be found using a predication model or experimentally. We illus-

trate the latter for I

EEE 802.11g using an AP of type Cisco AP-1200/AP21G [7] and

the network benchmarking tool N

ETIO. The transport layer protocol is the Trans-

mission Control Protocol (TCP). The TCP end-to-end throughput is measured by

continuously transmitting segments of 1 kB in size in one minute between a laptop

and a PC connected to the DS. The results are shown in Figure 11.4. The ﬁgure

shows both the physical-layer data rates on the radio interface as well as the TCP

end-to-end throughput. Experiments also show that the results are valid for both

downlink (AP to laptop) and uplink (laptop to AP). The measurement points of the

end-to-end throughput can be interpolated by means of a best-ﬁt polynomial (illus-

trated by the dotted curve in Figure 11.4), which we use to deﬁne t

for the instance

described in Section 11.9.

−90 −80 −70 −60 −50 −40 −30 −20

Received signal power, [dBm]

Throughput, [Mbps]

Nominal bit rate

Interpolated throughput

Measured throughput

Fig. 11.4 Nominal bit rate and end-to-end throughput as functions of received signal strength

292 S. Bosio et al.

11.5 AP Location Optimization

The AP location problem amounts to selecting a subset

A of the candidate locations

A for installing APs. It can be modeled as a variation of the facility location prob-

lem. A natural objective function is to maximize the total single-user throughput

over all TPs. We introduce two sets of variables:



1ifAPa is installed,

0 otherwise.



1ifTPi is served by AP a,

0 otherwise.

(11.1)

The model of maximum-throughput AP location (M

TAL) reads

max

∑

i∈I

∑

a∈A

(11.2a)

s. t. x

−z

≤ 0 i ∈ I ,a ∈A

(11.2b)

∑

a∈A

≤ 1 i ∈I (11.2c)

∑

a∈A

≤ M (11.2d)

∈{0,1} a ∈ A (11.2e)

∈{0,1} i ∈ I ,a ∈ A

(11.2f)

In M

TAL, the objective function (11.2a) is to maximize the average throughput

(and equivalently the total throughput) of the TPs. Constraints (11.2b) ensure that a

TP can be served by an AP only if the latter is installed. By constraints (11.2c), a

TP can be associated with and served by at most one AP. The next constraint sets a

maximum limit on the number of installed APs.

Note that there is no constraint requiring that all TPs have to be covered. Rather,

the model encourages coverage by rewarding a higher throughput. Furthermore, in

any optimal solution each TP will always be served by the AP providing the best sig-

nal strength and equivalently the highest throughput value. Observe also that there

is always an optimal solution in which constraint (11.2d) is tight, as adding APs

to a solution does not reduce the throughput. Finally, although the combinatorial

problem represented by M

TAL is generally NP-hard, in most of the practical cases

of WLAN planning the number of candidate AP locations is quite small (often less

than a hundred), and M

TAL can be solved by commercial integer-linear solvers in a

short time.