Koster A., Munoz X. Graphs and Algorithms in Communication Networks

Подождите немного. Документ загружается.

270 I. Sau, J.

Zerovnik

time, under the constraint that each edge can be used by at most one packet at the

same time.

Besides the constraints about the initial and ﬁnal positions of the packets, there

also exist different routing models at the intermediate nodes of the network. For

instance, in the hot potato model no packet can be stored at the nodes of the network,

whereas in the store-and-forward at each step a packet can either stay at a node or

move to an adjacent node. Another widely used model is wormhole routing [26].

On the other hand, one can consider constraints on the number of incident edges

that each node of the network can use to send or receive packets at the same time.

In the

-port model [11], each node can send or receive packets through all its

incident edges at the same time. Here we study the store-and-forward

-port model.

In addition, we suppose that cohabitation of multiple packets at the same node is

allowed. Thus, a queue is required for each outgoing edge at each node. We also

suppose that packets move in a synchronous way and that it takes exactly one time

unit for a packet to traverse a link.

The nature of the links of the network is another factor that inﬂuences the rout-

ing efﬁciency. The type of link is usually one of the following: full-duplex or half-

duplex. In the full-duplex case there are two links between two adjacent nodes, one

in each direction. Hence two packets can move, one in each direction, simultane-

ously. In the half-duplex case only one packet can move between two nodes, in

either direction of the edge. In this survey we consider both half- and full-duplex

links.

10.1.3 Topologies

We now give a brief summary of various cases of (,k)-routing and (1,any)-routing

that have been studied for several speciﬁc topologies. More precisely, we ﬁrst list

the most important results for some networks which have attracted a great interest

in the literature, such as hypercubes and circulant graphs. Then we move to plane

grids. It is well known that there exist only three possible tessellations of the plane

into regular polygons [32]: squares, triangles, and hexagons. These graphs are those

which we study in this survey.

10.1.3.1 Different Network Topologies

In [14] the authors studied the permutation routing problem in low-dimensional

hypercubes (d ≤12). They gave optimal or “good in the worst case” oblivious algo-

rithms, i.e., algorithms in which the path used by a packet is entirely determined by

its origin and its destination. Another network widely studied in the literature is the

two-dimensional mesh with row and column buses (with point-to-point communi-

cation). This network can also be diversiﬁed according to the capacities of the buses.

In [47] Suel gave a deterministic algorithm to solve the permutation routing problem

10 Permutation Routing 271

in such networks. It gives a schedule using at most n + o(n) steps and a queue of

size 2, where the queue is the maximum number of packets that have to be stored at

an intermediate node. He also proposed a deterministic algorithm for r-dimensional

arrays with buses working in (2 −

)n + o(n) steps and still using queues of size

2. In [22], the authors studied the (, )-routing problem in the mesh grid with two

diagonals and gave, for  ≥ 9, a deterministic algorithm using

2n

+(n

2/3

) steps.

In [13], the authors introduced an algorithm called big foot algorithm. The idea of

this algorithm is to identify two types of links and to move towards the destination

using ﬁrst the links of the ﬁrst type and then those of the second type. The algorithms

we develop will use such a strategy. Hwang, Lin, and Jan [13] gave an optimal

algorithm for the permutation routing problem in full-duplex 2-circulant graphs.

The same algorithm is optimal for double-loop networks, i.e., oriented 2-circulant

graphs. Recall that a circulant graph is a graph on n vertices in which the ith vertex

is adjacent to the (i + j)th and (i − j)th vertices (mod n) for each j in a list l of

positive integers.

Another network of great practical importance is the double-loop network: a net-

work modeled by a graph G =(V, E) with V = {v

,...,v

n−1

} such that there are

two integers h

and h

such that E = {v

i±h

: i = 0,...,n −1} (the indices

being taken modulo n). The permutation routing problem in this network is studied

in [9]. The authors gave an algorithm for the permutation routing problem which on

average uses 1.12 steps (the expected value being empirically measured). In [10],

an optimal centralized permutation routing algorithm in k-circulant graphs (k ≥ 2)

is given (with polylogarithmic time complexity for k = 2).

The problem has been also studied for packets arriving dynamically. In [12],

the author gave an optimal online schedule for the linear array. He also gave a 2-

approximation for rings and showed that, using shortest path routing, no better ap-

proximation algorithm exists. In [18], the authors studied Cube Connected Cycles:

CCC(n, 2

) (hypercubes of dimension n where each vertex is replaced by a cycle

of length n). They gave an algorithm working in O(n

) with O(1) buffers for the

online partial permutation routing (PPR).

10.1.3.2 Plane Grids

Maybe the most studied networks in the literature are the two-dimensional grids (or

plane grids), and among them in particular the n ×n = N square grid has deserved

special attention. Let us brieﬂy overview what has been previously done on (, k)-

routing in plane grids.

In [28] the ﬁrst running time 2n−2), and queues of size 1,008 appears. The queue

size is reduced in [38] to 112 and further in [44] to 81. Furthermore, in [44] the au-

thors provide another algorithm running in near-optimal time 2n+O(1) steps with a

maximum queue size of only 12. [31] gives an asymptotically optimal algorithm for

(1,k)-routing on plane grids, with queues of small constant size. They introduced

for the ﬁrst time the (1,k)-routing and the (1, any)-routing problems. This result was

further improved in [43], where the authors gave a near-optimal deterministic algo-

272 I. Sau, J.

Zerovnik

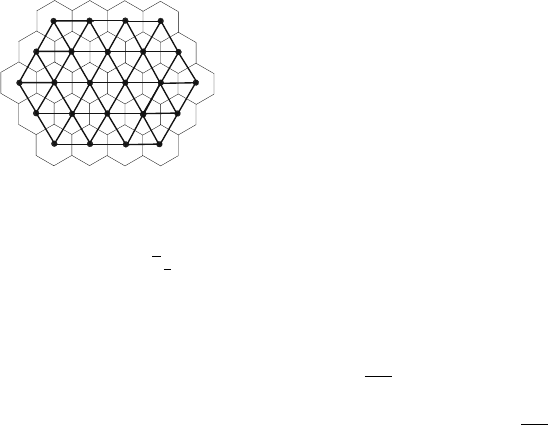
Fig. 10.1 Hexagonal network () and hexagonal tessellation ()

rithm running in

√

+ O(n) steps. Another algorithm was given that is slightly

worse in terms of number of steps, but with queues of size only 3. In the same pa-

per, lower bounds and near-optimal randomized and deterministic algorithms were

proposed for the general problem of (, k)-routing on square grids. The algorithms

were also extended to higher dimensional meshes which performed (, )-routing

in O(n) steps, the lower bound being

(

√

kn) for (, k)-routing [43]. Finally,

in [35], the authors gave deterministic and randomized algorithms for (,k)-routing

on square grids, with constant queue size. The running time is O(

√

kn) steps, which

is optimal according to the bound of [43]. This work closed a gap in the literature,

since optimal algorithms were only known for  = 1 and  = k. Oblivious permuta-

tion routing algorithms were given by Iwama and Miyano [16, 17] and Litman and

Moran-Schein [29]. For generalization to d-dimensional meshes and (k,k)-routing

see [15, 23, 33]. On triangular and hexagonal grids, the best results are randomized

algorithms with good performance [42].

Nodes on a hexagonal network are placed at the vertices of a regular triangular

tessellation, so that each node has up to six neighbors. These networks have been

studied in a variety of contexts, especially in wireless and interconnection networks.

The most known application may be to model cellular networks with hexagonal

networks where nodes are base stations. Furthermore, these networks have been

also applied in chemistry to model benzenoid hydrocarbons [20, 48], and in image

processing and computer graphics [21].

In a radiocommunication wireless environment [32], the interconnection network

among base stations constitutes a hexagonal network, i.e., a triangular grid, as it is

shown in Figure 10.1.

Tessellation of the plane with hexagons may be considered as the most natural

because cells have optimal diameter to area ratio (in the sense that this ratio is greater

than in square or triangular grids). Hexagonal networks are ﬁnite subgraphs of the

triangular grid. The triangular grid can also be obtained from the basic 4-mesh by

adding NE to SW edges, which is called a 6-mesh in [49]. Here we study convex

subgraphs of the square, triangular, and hexagonal grids.

In the next section we brieﬂy outline some results on the permutation routing

problem on hexagonal grids. Some details are given in order to illustrate the main

ideas that can be applied to other grids with some natural modiﬁcations. We use the

10 Permutation Routing 273

store-and-forward

-port model, and consider both full- and half-duplex networks.

Recall that here we assume there are no bounds on the queue size.

10.2 Optimal Permutation Routing Algorithm

10.2.1 Preliminaries

Nodes on a hexagonal network are placed at the vertices of a regular triangular

tessellation, so that each node has up to six neighbors. We deal in this section with

a hexagonal mesh network G =(V,E) with full-duplex links, that is, an edge of

the network can be crossed by two simultaneous messages, one in each direction.

Equivalently, each edge between two vertices u and v is made of two independent

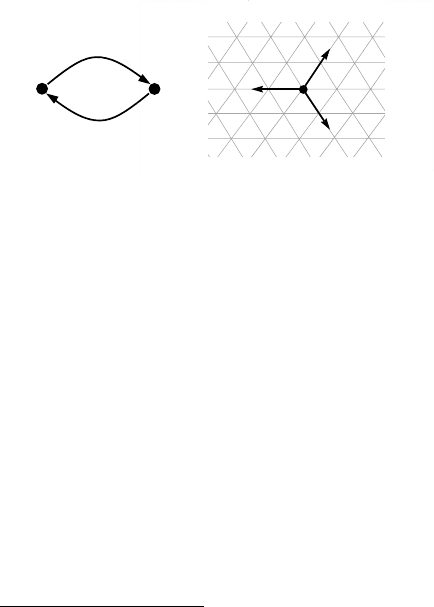
arcs (u,v) and (v,u), as illustrated in Figure 10.2a.

O=(0,0,0)

Fig. 10.2 a) Each edge consists of two independent links. b) Axis used in a hexagonal network

In [32] the authors solved the problem of routing a single message through a

hexagonal communication network. The idea (ﬁrst introduced in [46]) that will be

very useful later is the representation of any address in a basis consisting of three

unitary vectors i, j, k on the directions of the three axes x,y, z with a 120

◦

angle be-

tween them, intersecting on an arbitrary (but ﬁxed) node O labeled with the address

O =(0, 0,0), as depicted in Figure 10.2b.

Thus, assume that each vertex P ∈V is labeled with an address P =(P

)

expressed in this basis {i, j, k} with respect to the origin O. At the beginning, each

vertex S knows the address of the destination vertex D of the message placed initially

at S, and computes the relative address

−→

SD = D −S of the message. Note that this

relative address does not depend on the choice of the origin vertex O. This relative

An optimal permutation routing on full-duplex hexagonal networks was ﬁrst given in [40], as a

result of a STSM within COST 293.

274 I. Sau, J.

Zerovnik

address is the only information that is added in the heading of the message to be

transmitted, constituting in this way the packet to be sent through the network.

Using i + j + k = 0, the key observation [32] is that if (a,b, c) and (a



) are

the relative addresses of two packets, then (a, b,c)=(a



) if and only if there

exists a d ∈ Z such that a



= a + d, b



= b + d, and c



= c + d.

Deﬁnition 10.1. An address

−→

SD =(a,b,c) is of the shortest path form if there is a

path from vertex S to vertex D, consisting of a units of vector i, b units of vector j,

and c units of vector k, and this path has the shortest length.

The next result simpliﬁes extraordinarily the routing in hexagonal networks.

Theorem 10.3 ( [32]). An address (a,b,c) is of the shortest path form if and only if

at least one component is zero, and any two components do not have the same sign.

Corollary 10.1 ( [32]). Any address has a unique shortest path form.

Thus, each address

−→

SD written in the shortest path form has at most two nonzero

components, and they have different signs. In fact, it is easy to ﬁnd the shortest path

form using the next result.

Theorem 10.4 ( [32]). If

−→

SD = ai + bj + ck, then

−→

SD|= min(|a −c|+ |b −c|,|a −b|+ |b

−c|,|a −b|+ |a −c|).

10.2.2 Description of the Algorithm for Hexagonal Networks

Many communication networks are represented by graphs satisfying the following

property: for any pair of vertices u and v, the edges of a shortest path from u to v

can be partitioned into k disjoint classes according to a well-deﬁned criterion. For

instance, we have seen in Section 10.2.1 that on a hexagonal network the edges of

a shortest path can be partitioned into positive and negative ones. Similarly, on a k-

circulant graph the edges can be partitioned into k classes according to their length.

In graphs that satisfy this property there exists a natural routing algorithm: route

all packets along one class of edges one after another. Surprisingly, in many cases

this natural algorithm turns out to be optimal. Optimality for 2-circulant graphs is

proved using a static approach in [13], and recently using a dynamic distributed

algorithm in [39]. The algorithm is called the big-foot algorithm because it routes

packets ﬁrst along long hops and then along short hops in a 2-circulant graph [13].

There is no restriction on the size of the queues. On the square grid, the big-foot

idea works as is natural, i.e., an optimal algorithm consists of two phases, moving

each packet ﬁrst horizontally and then vertically.

Based on the observations on the addressing scheme of hexagonal networks, it

can be proved that for hexagonal networks this algorithm turns out to be also optimal

[40].

The optimal algorithm A is completely distributed, and can be described as fol-

lows. At each node u of the network, perform:

10 Permutation Routing 275

I. Preprocessing phase. If there is a packet at node u, the preprocessing phase con-

sists just of computing the relative address D −S of the message in the shortest

path form, and adding this information to the message to complete the packet

to be sent. Recall that because of Theorem 10.3, D −S can have no more than

one negative component. At each step, when a packet is received at u, its relative

address is updated.

II. Transmission phase. Repeat:

a) If there are packets with negative components, send them immediately along

the direction of this component.

b) If not, for each outgoing edge order the packets according to a decreasing

number of remaining steps and send the ﬁrst packet of each queue.

10.2.3 Correctness, Running Time and Optimality

Algorithm A is really cheap in terms of computational cost, since the only involved

operations are integer addition and comparison among the lengths of the addresses

of the packets at each node. Let us brieﬂy discuss correctness and give the main

ideas of the proof of optimality.

The rules given by Algorithm A deﬁne two directions of movement for each

packet. That is, ﬁrst of all a packet moves along the direction of its negative com-

ponent, and then along its positive one. Obviously, if a packet has only positive

component, it always moves along this direction. The ﬁrst key observation is that

packets can only wait, possibly, during their last direction. That is because if two

packets meet when their ﬁrst direction is not ﬁnished yet, it is easy to check that

they must have the same origin node, a contradiction. Thus, in a) there can be at

most one packet with a negative component at each outgoing edge; hence, there is

no ambiguity. Finally, in b) the packet with maximum remaining length at each out-

going edge is unique, since all these packets are moving along their last direction

(their negative component is already ﬁnished; otherwise, they would be in a)) and

each node is the destination of at most one packet.

Using this algorithm, at every step all packets with maximum remaining distance

move, and hence at every step the maximum remaining distance over all packets

decreases by 1. Thus, the total running time is at most 

max

, meeting the lower

bound. More details can be found in [40]. In the case of permutation routing, we

have proved that the number of steps i at each node is at most 

max

, but written in this

way the algorithm can be applied in a more general routing scenario. In conclusion,

the main result can be summarized as follows.

Theorem 10.5 (see [40]). Algorithm A is an optimal permutation routing algorithm

for full-duplex hexagonal networks.

Besides minimizing the number of steps, a routing algorithm must also be easy to

implement; namely, the routing at each step should be determined efﬁciently. Recall

276 I. Sau, J.

Zerovnik

that a routing algorithm is called oblivious if the path of a packet from v depends

only on v and its destination, although the waiting time at an intermediate node may

depend on other paths. Furthermore, a translation invariant oblivious algorithm is

completely determined by paths from the origin.

The obliviousness of A is straightforward since the routing for each packet de-

pends only on the source and destination nodes. Finally, it is clear that to route a

packet only the difference D−S between the source and destination node is needed,

and thus we have proved the invariance.

Corollary 10.2 (see [40]). Algorithm A is an oblivious, translation invariant, and

optimal permutation routing algorithm for full-duplex hexagonal mesh networks.

10.3 Extensions and Open Problems

The algorithm described in Section 10.2.2 can be extended to ﬁnd optimal permu-

tation routing algorithms for all the other types of plane grids, as well as for ﬁnding

near-optimal algorithms for (,k)-routing for all types of plane grids. The following

results can be found in [1]:

1. A tight (also including the constant factor) permutation routing algorithms in

full-duplex hexagonal grids and half-duplex triangular and hexagonal grids.

2. A tight (also including the constant factor) r-central routing algorithms in tri-

angular and hexagonal grids. It may be interesting to remark that the optimal

algorithms for r-central routing slightly deviate from the general scheme of the

permutation routing algorithms.

3. A tight (also including the constant factor) (k,k)-routing algorithms in square,

triangular, and hexagonal grids.

4. Approximation algorithms for (,k)-routing in square, triangular, and hexagonal

grids.

Of course, there are many questions to be asked. For instance, the words approx-

imation algorithms mentioned above mean that there is no optimal (or even tight)

algorithm for (,k)-routing known for any plane grid. This is deﬁnitely the most

challenging open problem concerning (,k)-routing on plane grids.

There are other important avenues for further research. An important issue is to

optimize also the maximum size of the queues at the nodes. We have not addressed

this point here, mostly because often when optimizing the queue size the running

time increases. Finding the right trade-off between both parameters would be a cel-

ebrated result.

Finally, observe that all the graphs discussed in Section 10.2.2 are Cayley graphs,

with their corresponding generators. In fact, the generators of each type of graph in-

duce the partition of the shortest paths into the k mentioned sets. Therefore, it seems

natural that this idea of routing packets one class after another could be extended to

any Cayley graph, which would be a quite general result.

10 Permutation Routing 277

Acknowledgements We want to thank Omid Amini, Fr

eric Giroire, Florian Huc, and Rastislav

alovi

c for insightful remarks and discussions.

References

1. Amini, O., Huc, F., Sau, I.,

Zerovnik, J.: (,k)-Routing on Plane Grids. Rapport de Recherche

6480 INRIA (2008)

2. Aspnes, J., Azar, Y., Fiat, A., Plotkin, S., Waarts, O.: On-line routing of virtual circuits with

applications to load balancing and machine scheduling. Journal of the ACM (JACM) 44(3),

486–504 (1997)

3. Aspnes, J., Busch, C., Dolev, S., Fatourou, P., Georgiou, C., Shvartsman, A.: Eight Open

Problems in Distributed Computing. Bulletin of the EATCS 90, 109–126 (2006)

4. Awerbuch, B., Azar, Y.: Local optimization of global objectives: competitive distributed dead-

lock resolution and resource allocation. In: 35th Annual Symposium on Foundations of Com-

puter Science (FOCS), pp. 240–249 (1994)

5. Azar, Y., Cohen, E., Fiat, A., Kaplan, H., R

acke, H.: Optimal oblivious routing in polynomial

time. Journal of Computer and System Sciences 69(3), 383–394 (2004)

6. Borodin, A., Hopcroft, J.: Routing, merging and sorting on parallel models of computation.

Proceedings of the fourteenth annual ACM symposium on Theory of computing pp. 338–344

(1982)

7. Busch, C., Magdon-Ismail, M., Xi, J.: Oblivious routing on geometric networks. Proceedings

of the 17th annual ACM symposium on Parallelism in algorithms and architectures pp. 316–

324 (2005)

8. Busch, C., Magdon-Ismail, M., Xi, J.: Optimal oblivious path selection on the mesh. Pro-

ceedings of the International Parallel and Distributed Processing Symposium (IPDPS 2005),

Denver, Colorado, USA, April (2005)

9. Dobravec, T., Robi

c, B.,

Zerovnik, J.: Permutation routing in double-loop networks: design

and empirical evaluation. Journal of Systems Architecture 48, 387–402 (2003)

10. Dobravec, T.,

Zerovnik, J., Robi

c, B.: An optimal message routing algorithm for circulant

networks. Journal of Systems Architecture 52, 298–306 (2006)

11. Fraigniaud, P., Lazard, E.: Methods and problems of communication in usual networks. Dis-

crete Applied Mathematics 53, 79–134 (1994)

12. Havill, J. T.: Online Packet Routing on Linear Arrays and Rings. Lecture Notes in Computer

Science 2076, 773–784 (2001)

13. Hwang, F., Lin, T., Jan, R.: A Permutation Routing Algorithm for Double Loop Network.

Parallel Processing Letters 7(3), 259–265 (1997)

14. Hwang, F., Yao, Y., Dasgupta, B.: Some permutation routing algorithms for low-dimensional

hypercubes. Theoretical Computer Science 270, 111–124 (2002)

15. Iwama, K., Kambayashi, Y., Miyano, E.: New Bounds for Oblivious Mesh Routing. Journal

of Graph Algorithms and Applications 5(5), 17–38 (2001)

16. Iwama, K., Miyano, E.: Oblivious Routing Algorithms on the Mesh of Buses. Journal of

Parallel and Distributed Computing 60, 137–149 (2000)

17. Iwama, K., Miyano, E.: An O(

√

N) Oblivious Routing Algorithm for Two-Dimensional

Meshes of Constant Queue-Size. Journal of Algorithms 41, 262–279 (2001)

18. Jan, G. E., Lin, M. B.: Concentration, load balancing, partial permutation routing, and super-

concentration on cube-connected cycles parallel computers. Journal of Parallel and Distributed

Compututing 65, 1471–1482 (2005)

19. Kaklamanis, C., Krizanc, D., Tsantilas, T.: Tight bounds for oblivious routing in the hyper-

cube. Theory of Computing Systems 24(1), 223–232 (1991)

20. Klav

zar, S., Vesel, A.,

Zigert, P.: On resonance graphs of catacondensed hexagonal graphs:

structure, coding, and Hamiltonian path algorithm. MATCH Communications in Mathemati-

cal and in Computer Chemistry 49(49), 99–116 (2003)

278 I. Sau, J.

Zerovnik

21. Kranakis, E., Sing, H., Urrutia, J.: Compas Routing in Geometric Graphs. In: 11th Canadian

Conference of Computational Geometry, pp. 51–54 (1999)

22. Kunde, M., Niedermeier, R., Rossmanith, P.: Faster sorting and routing on grids with diago-

nals. In: 11th Symposium of Theoretical Computer Science, 775, pp. 225–236. Lecture Notes

on Computer Science (1994)

23. Kunde, M., Tensi, T.: (k −k) Routing on Multidimensional Mesh-Connected Arrays. Journal

of Parallel and Distributed Computing 11, 146–155 (1991)

24. Leighton, F., Maggs, B. M., Richa, A. W.: Fast Algorithms for Finding O(Congestion + Dila-

tion) Packet Routing Schedules. In: 28th Annual Hawaii International Conference on System

Sciences, pp. 555–563 (1995)

25. Leighton, F. T., Maggs, B. M., Rao, S. B.: Packet Routing and Job-Shop Scheduling in

O(congestion + dilation) Steps. Combinatorica 14(2), 167–186 (1994)

26. Leighton, T.: Introduction to Parallel Algorithms and Architectures: Arrays-Trees-

Hypercubes. Morgan-Kaufman, San Mateo, California (1992)

27. Leighton, T., Maggs, B., Rao, S.: Universal packet routing algorithms. In: 29th Annual Sym-

posium on Foundations of Computer Science (FOCS), pp. 256–269 (1988)

28. Leighton, T., Makedon, F., Tollis, I. G.: A 2n−2 Step Algorithm for Routing in an n×n Array

with Constant-Size Queues. Algorithmica 14, 291–304 (1995)

29. Litman, A., Moran-Schein, S.: Fast, minimal, and oblivious routing algorithms on the mesh

with bounded queues. Journal of Interconnection Networks 2, 445–469 (2001)

30. Maggs, B.: A Survey of Congestion + Dilation Results for Packet Scheduling. 40th Annual

Conference on Information Sciences and Systems 22(24), 1505–1510 (2006)

31. Makedon, F., Symvonis, A.: Optimal algorithms for the many-to-one routing problem on 2-

dimensional meshes. Microprocessors and Microsystems 17, 361–367 (1993)

32. Nocetti, F. G., Stojmenovi

c, I., Zhang, J.: Addressing and Routing in Hexagonal Networks

with Applications for Tracking Mobile Users and Connection Rerouting in Cellular Networks.

IEEE Transactions on Parallel and Distributed Systems 13(9), 963–971 (2002)

33. Osterloh, A.: Optimal oblivious routing on d-dimensional Meshes. Theoretical Computer

Science 333, 331–346 (2005)

34. Ostrovsky, R., Rabani, Y.: Universal O(congestion + dilation + log

N) Local Control Packet

Switching Algorithms. In: 29th Annual ACM Symposium on the Theory of Computing, pp.

644–653. New York (1997)

35. Pietracaprina, A., Pucci, G.: Optimal Many-to-One Routing on the Mesh with Constant

Queues. Lecture Notes in Computer Science 2150, 645–649 (2001)

36. R

acke, H.: Exploiting locality for data management in systems of limited bandwidth. In: 38th

Annual Symposium on Foundations of Computer Science (FOCS), pp. 284–293 (1997)

37. R

acke, H.: Minimizing congestion in general networks. In: 43rd Annual Symposium on Foun-

dations of Computer Science (FOCS), pp. 43–52 (2002)

38. Rajasekaran, S., Overholt, R.: Constant queue routing on a mesh. Journal of Parallel and

Distributed Computing 15, 160–166 (1992)

39. Robi

c, B.,

Zerovnik, J.: Minimum 2-terminal routing in 2-jump circulant graphs. Computers

and Artiﬁcial Intelligence 19(1), 37–46 (2000)

40. Sau, I.,

Zerovnik, J.: An Optimal Permutation Routing Algorithm on Full-Duplex Hexagonal

Networks. Discrete Mathematics and Theoretical Computer Science 10(3), 49–62 (2008)

41. Scheideler, C.: Universal Routing Strategies for Interconnection Networks. Springer (1998)

42. Sibeyn, J.: Routing on Triangles, Tori and Honeycombs. International Journal of Foundations

of Computer Science 8(3), 269–287 (1997)

43. Sibeyn, J., Kaufman, M.: Deterministic 1-k routing on meshes (with applications to worm-

hole routing). In: LNCS (ed.) 11th Symposium on Theoretical Aspects of Computer Science,

vol. 775, pp. 237–248 (1994)

44. Sibeyn, J. F., Chlebus, B. S., Kaufmann, M.: Deterministic Permutation Routing on Meshes.

Journal of Algorithms 22(1), 111–141 (1997)

45. Srinivasan, A., Teo, C. P.: A constant-factor approximation algorithm for packet routing, and

balancing local vs. global criteria. In: STOC ’97: Proceedings of the Twenty-Ninth Annual

ACM Symposium on Theory of Computing, pp. 636–643. ACM, New York, NY, USA (1997).

DOI http://doi.acm.org/10.1145/258533.258658

10 Permutation Routing 279

46. Stojmenovi

c, I.: Honeycomb Networks: Topological Properties and Communication Algo-

rithms. IEEE Transactions on Parallel and Distributed Systems 8(10), 1036–1042 (1997)

47. Suel, T.: Routing and Sorting on Meshes with Row and Column Buses. In: Parallel Processing

Symposium, vol. Eighth International Volume, pp. 411–417 (1994)

48. To

c, R., Masulovi

c, D., Stojmenovi

c, I., Brunvoll, J., Cyvin, B., Cyvin, S.: Enumeration of

Polyhex Hydrocarbons up to h=17. Journal of Chemical Information and Computer Sciences

35, 181–187 (1995)

49. Trobec, R.: Two-dimensional regular d-meshes. Parallel Computing 26, 1945–1953 (2000)

50. Valiant, L., Brebner, G.: Universal schemes for parallel communication. Proceedings of the

thirteenth annual ACM symposium on Theory of computing pp. 263–277 (1981)