Кошак Ж.В, Минина Е.М. Применение ЭВМ в отрасли
Подождите немного. Документ загружается.

31
у = b
0
+b
1
z
1
+b
2
z
2
+b
3
z
3
=b
0
+∑(b
i
z
i
)
(37)
После введения фиктивной переменной z
0
=l, y=∑(b
i
z
i
).
Полный факторный эксперимент дает возможность найти раздельные
оценки коэффициентов b
i
.
Нахождение модели методом полного факторного эксперимента состоит из
планирования эксперимента, собственно эксперимента, проверки
воспроизводимости (однородности выборочных дисперсий), получения
математической модели объекта с проверкой статистической значимости
выборочных коэффициентов регрессии и проверки адекватности математического
описания.
Построим матрицу планирования для трехфакторной задачи. При этом
следует помнить, что полный факторный эксперимент — это весь возможный
перебор неповторяющихся комбинаций уровней x
i:
Матрицу удобно начать со строки (под строкой, как и в исходном журнале
первичных данных, понимают условия и результат одного опыта), где все
управляемые переменные находятся на нижнем уровне, т. е. z
1
=-1, Z
2
=-1, Z
3
=-1.
Последующие строки (многомерные точки) выбираются по правилу: при
построчном переборе всех вариантов частота смены знака управляемых
переменных для каждой последующей переменной вдвое меньше; чем для
предыдущей. Поскольку все переменные могут принимать только значения +1 и
—1, это позволяет в целях упрощения записывать в матрицу только знаки « + » и
«-». Фиктивная переменная z
0
во всех строчках имеет знак " + ". Количество
строчек 2
n
= 2
3
=8.
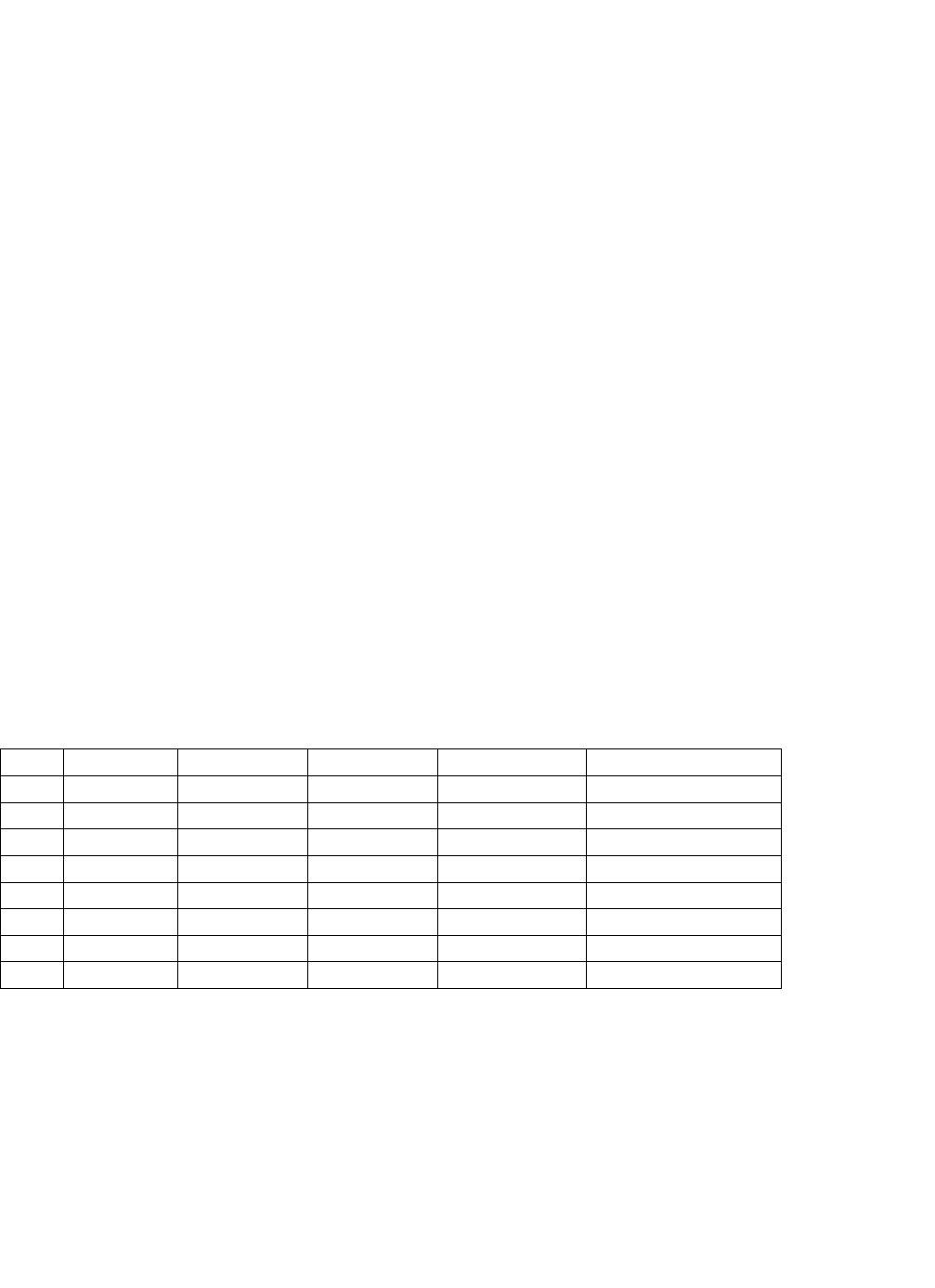
Таблица 9 - Матрица планирования трехфакторного эксперимента
Z
0
Z
1
Z
2
Z
3
Y
1 + - - - Y
1
2 + + - - Y
2
3 + - + - Y
3
4 + + + - Y
4
5 + - - + Y
5
6 + + - + Y
6
7 + - + + Y
7
8 + + + + Y
8
Число строчек матрицы планирования, т. е. число опытов, возрастает по
показательной функции 2
n
.
Построенный таким способом план эксперимента обладает рядом ценных
свойств:
1. Симметричность относительно центра эксперимента: алгебраическая
сумма элементов столбцов для каждого фактора равна нулю ∑z
ji
= 0 [где i -
номер фактора (меняется от 1 до n); j - номер опыта (меняется от 1 до N).
2. Условие нормировки: сумма квадратов элементов каждого столбца равна
числу опытов ∑z
2
ij
= N.

32
3. Сумма почленных произведений любых двух столбцов матрицы
планирования равна нулю: ∑z
ij
z
ky
=0 i≠k, i, k=0, 1, 2, .... п.
Это важное свойство называется ортогональностью. Поэтому такие планы и
их матрицы называют ортогональными.
Из последнего свойства следует взаимная независимость оценок
коэффициентов уравнения регрессии.
При реализации полного факторного эксперимента, поскольку изменение
выходной величины у носит случайный характер, приходится в каждой
многомерной точке проводить т параллельных опытов и результаты наблюдений
у
j1
, у
j2
, .... у
jl
.....y
jm
усреднять:
∑
=
=
m
i
jl
j
m
y
y
1
(38)
Весь эксперимент в этом случае делится на т серий опытов, в каждой из которых
полностью реализуется матрица планирования.
Прежде чем строить математическую модель по результатам опытов,
необходимо проверить, не было ли влияния на некоторые из них неучтенных
факторов. Проверка воспроизводимости представляет собой проверку
выполнения предпосылки регрессионного анализа об однородности выборочных
дисперсий S
2
yi
Задача состоит в проверке гипотезы о равенстве дисперсий S
2
y1
= S
2
y2
=
S
2
y3
=…= S
2
yn
, при экспериментах во всех многомерных точках (8 точек для трех
факторов). Оценки дисперсий находят по формуле
1
)(y
m
1
2
jl
2
−
−
=
∑
=
m
y
S
i
j
yj
(39)
Если каждый опыт проводился трижды, та дисперсии получают по
выборкам одинакового объема m=3, a число степеней свободы для всех дисперсий
одинаково и равно т - 1=2.
Для проверки гипотезы об однородности оценок дисперсий следует
пользоваться критерием Кохрена G, который основан на законе распределения
отношения максимальной полученной дисперсии к сумме всех дисперсий.
Расчетное значение критерия получают по формуле:
∑
=
2
yj
2
макс
S
yj
p
S
G
(40)
Для нахождения табличного значения критерия Кохрена рассчитывают f
1
=m-1;
f
2
=N. Если вычисленное значение критерия G
p
окажется меньше его табличного
значения G
т
, для выбранного уровня значимости (обычно α=0,05), то гипотеза об
однородности дисперсий принимается. Это значит, что различий между
дисперсиями не должно быть.

33
В этом случае можно рассчитать генеральную дисперсию
воспроизводимости
2
воспр
1
2
2
S
N
S
S
n
j
yj
y
==
∑
=
(41)
Имеющую f
3
==N(m— 1) степеней свободы.
Если проверка на воспроизводимость дала отрицательный результат, то
остается признать невоспроизводимость эксперимента относительно управляемых
переменных вследствие флуктуации неуправляемых и неконтролируемых
переменных, создающих на выходе большой уровень «шума». При этом следует
повторить эксперимент с увеличенным числом параллельных опытов.
Построение математической модели объекта начинается с определения
независимых оценок - коэффициентов b
i
по формуле:
N
yz
b
n
i
ii
i
∑
=
=
1
(42)
После этого необходимо проверить гипотезу о значимости коэффициентов
b
i
, (проверка нуль-гипотезы b
i
=0).
Проверка гипотезы проводится с помощью t-критерия, который в данном
случае формируется как
bi
i
p
S
b
t =
(43)
где S
bi
— среднеквадратическая ошибка, определения коэффициента b
i
при
полном факторном эксперименте, равная
Nm
S
S
y
bi
2
=
(44)
Если найденная величина параметра t превышает значение t
кр
,
определенное по таблицам Стьюдента для числа степеней свободы f=N(m - 1) при
заданном уровне значимости, т. е. sgn(t
p
— t
кр
) = «+», то гипотеза отвергается и
коэффициент b
i
признается значимым.
В противном случае, если sgn(t
p
— t
кр
) =«–», нуль-гипотеза принимается и
коэффициент b
i
- считают статистически не значимым (т. е. равным нулю).
Значимость коэффициентов можно оценить с помощью доверительного
интервала:
∆b
j
=±t(N(m-1), α/2)⋅S
bj
(45)
Коэффициент полагается значимым, если выполняется неравенство:
Abs(b
j
)>= ∆b
j
где abs(b
j
) – значения коэффициентов по модулю.
Статистическая незначимость коэффициента b
i
может быть обусловлена
следующими причинами:

34
1) уровень базового режима x
i0
близок к точке частного экстремума по
переменной X
i
(или по произведению переменных);
2) шаг варьирования ∆x
i
- выбран малым;
3) данная переменная (произведение переменных) не имеет
функциональной связи с выходным параметром y, т. e. b
i
= 0 по существу;
4) велика ошибка эксперимента вследствие флуктуации неуправляемых и
неконтролируемых переменных.
Поскольку ортогональное планирование позволяет определять независимые
оценки коэффициентов, то если какой-либо из коэффициентов окажется
незначимым, он может быть отброшен без пересчета всех остальных.
После этого математическая модель объекта составляется в виде уравнения
связи выходного параметра у и переменных х
i
, включающего только значимые
коэффициенты.
Чтобы, проверить гипотезу об адекватности результатов эксперимента
найденным по уравнению связи, достаточно оценить отклонение предсказанной
уравнением регрессии выходной величины у
iр
от результатов эксперимента у
i
в
точках факторного пространства.
Разброс результатов эксперимента относительно линии регрессий в этом
случае сравнивается с разбросом точек между собой. Первый разброс
характеризуется дисперсией адекватности S
2
ад
, оценка которой находится по
формуле
d
N
yy
S
n
i
ipi
−
−
=
∑
=1
2
2
ад
)(
(46)
где d — число значимых коэффициентов линейного уравнения при числе
степеней свободы f
ад
=N—n—1.
Второй (разброс точек) — дисперсией воспроизводимости S
2
воспр
с числом
степеней свободы f
воспр
=N(m-1). Дисперсия воспроизводимости определяется по
формуле (41).
Если S
2
ад
< <S
2
воспр
, то полученная математическая модель адекватно
представляет результаты эксперимента.
Если S
2
ад
>S
2
восп
то нужно выяснить, случайно или не случайно различаются
эти дисперсии, и если не случай но, то делается вывод о неадекватности
уравнения.
Проверка гипотезы об адекватности проводится с использованием критерия
Фишера.
(47)
Если F
эксп
<F
Kp
для соответствующих степеней свободы f
ад
=N-d=N-n-1 и
f
воспр
=N(т— 1) при заданном уровне значимости а, то нуль-гипотеза принимается,
т. е. уравнение адекватно при sgn(F
эксп
—F
кр
)="-". В противном случае гипотеза
отвергается и описание признается неадекватным объекту.
Проверка адекватности возможна при f
ад
>0.
2
2
y
ад
эксп
S
S
F =

35
Если гипотеза об адекватности отвергается, необходимо переходить к более
сложной форме уравнения либо (если это возможно) проводить эксперимент с
меньшим шагом варьирования ∆х
i
.
Если математическая модель адекватна, то проверяют ее
работоспособность. Проверка работоспособности осуществляется при помощи
коэффициента детерминации. Расчет коэффициента детерминации может быть
осуществлен по формуле (14). Если значение R
2
> 0,7 то математическая модель
является работоспособной. В противном случае математическую модель нельзя
использовать для прогнозирования результатов, т.к. она не является
работоспособной.
5.2 Построение эксперимента в пакете Statgraphics Plus
Для построения эксперимента выполняются следующие действия:
1. Открывается пакет STATGRAPHICS PLUS.
2. Выбирается меню Special, подменю Experimental Design, команду
Create Design.
3. В открывшемся диалоговом окне в области Design Class
устанавливается маркер напротив команды Screening. В строке No. of Response
Variables устанавливается 1. В строке No. of Experimental Factors
устанавливается 3. Нажимается кнопка Ok.
4. Для каждого из трех факторов выставляются значения нижнего (-1,0)
и верхнего (1,0) уровней. Даются названия каждому фактору.
5. В следующем диалоговом окне в строке Name дается имя выходного
показателя, на который оказывают влияние факторы, указанные в предыдущем
окне.
6. В следующем диалоговом окне выбирается, какой эксперимент
необходимо провести (ПФЭ 2
3
).
7. В следующем диалоговом окне убирается галочка напротив команды
Randomize.
8. После чего открываем расчетную таблицу, в которую вносятся
средние значения выходного показателя Y.
9. Сохраняем документ.
10. В окне Screening Design Attributes выбирается на панели
инструментов кнопка Tabular Options.
11. В открывшемся диалоговом окне нажимается кнопка All.
12. Выбирается меню Special, подменю Experimental Design команда
Analyze Design.
13. В диалоговом окне Analyze Design выбирается параметр Y.
14. В окне Analyze Experimental на панели инструментов выбирается
кнопка Graphical Options. В открывшемся диалоговом окне нажимается кнопка
All. В результате в окне программы отобразятся все расчеты и графические
зависимости.

36
5.3 Анализ математической модели и результатов эксперимента
Коэффициенты при независимых переменных указывают на силу влияния
факторов: чем больше численная величина коэффициента, тем большее влияние
оказывает фактор. Если коэффициент имеет знак « + », то с увеличением значения
фактора параметр оптимизации у увеличивается, а если «-» - уменьшается.
Величина коэффициента соответствует вкладу данного фактора в величину
параметра оптимизации при переходе фактора с нулевого уровня на верхний или
на нижний.
Иногда удобно оценивать вклад фактора при переходе от нижнего уровня к
верхнему (либо наоборот), а не к нулевому. Вклад, определенный таким образом,
называется эффектом фактора (иногда его называют основным или главным
эффектом). Он численно равен удвоенному коэффициенту. Для качественных
факторов, варьируемых на двух уровнях, основной (нулевой) уровень зачастую не
имеет физического смысла. Поэтому понятие «эффект фактора» является здесь
естественным.
Известно, что большинство тепло-, массообменных и других
технологических процессов пищевой .промышленности подчиняются степенной
(у = х
т
an
) или экспоненциальной (у=a exp x) закономерности.
Вместе с тем никаких затруднений в описаний этих закономерностей
уравнениями в виде полиномов и физической интерпретации результатов нет.
Известно, что «выравнивание», или линеаризация степенного уравнения,
производится логарифмированием его обеих, частей, а экспоненциального
уравнения - только правой его части. После этого факторы заменяют
логарифмами и производят все расчеты как для обычного уравнения регрессии.
Отклик в первом случае также заменяется его логарифмом. Выравнивать можно и
большинство других закономерностей.
Таким образом, возможности физической интерпретации уравнений в
полиномах шире, чем других, поскольку они позволяют учесть взаимное влияние,
или эффекты взаимодействия факторов.
Более полной формой анализа результатов является геометрическая
интерпретация результатов ПФЭ.
Известно, что графически можно показать только непрерывную связь между
двумя переменными. Зависимости функции от других аргументов можно
изобразить дискретно, т. е. параметрически, или непрерывно, но в искаженном
виде с помощью аксонометрических построений. При интерпретации результатов
ПФЭ используются оба эти метода, но предпочтение отдается первому вследствие
его простоты.
Например, изучалось влияние гидротермической обработки риса-зерна на
пищевую (биологическую) ценность рисовой каши. Обработка состояла в
пропаривании зерна, поэтому в качестве факторов были приняты время
пропаривания x
1
, и давление пара x
2
. За функцию отклика у принята атакуемость
белков каши, сваренной из обработанного зерна, одним из пищеварительных
ферментов - пепсином.
37
Уравнение регрессии, полученное в результате ПФЭ, является неполным
квадратный уравнением: у= 179.75 – 18.25z
1
– 8,75z
2
– 25,75z
1
z
2
. Это уравнение
также удовлетворило всем требованиям статистического анализа (проверка
значимости коэффициентов с помощью (t-критерия, проверка адекватности
уравнения по F-критерию).
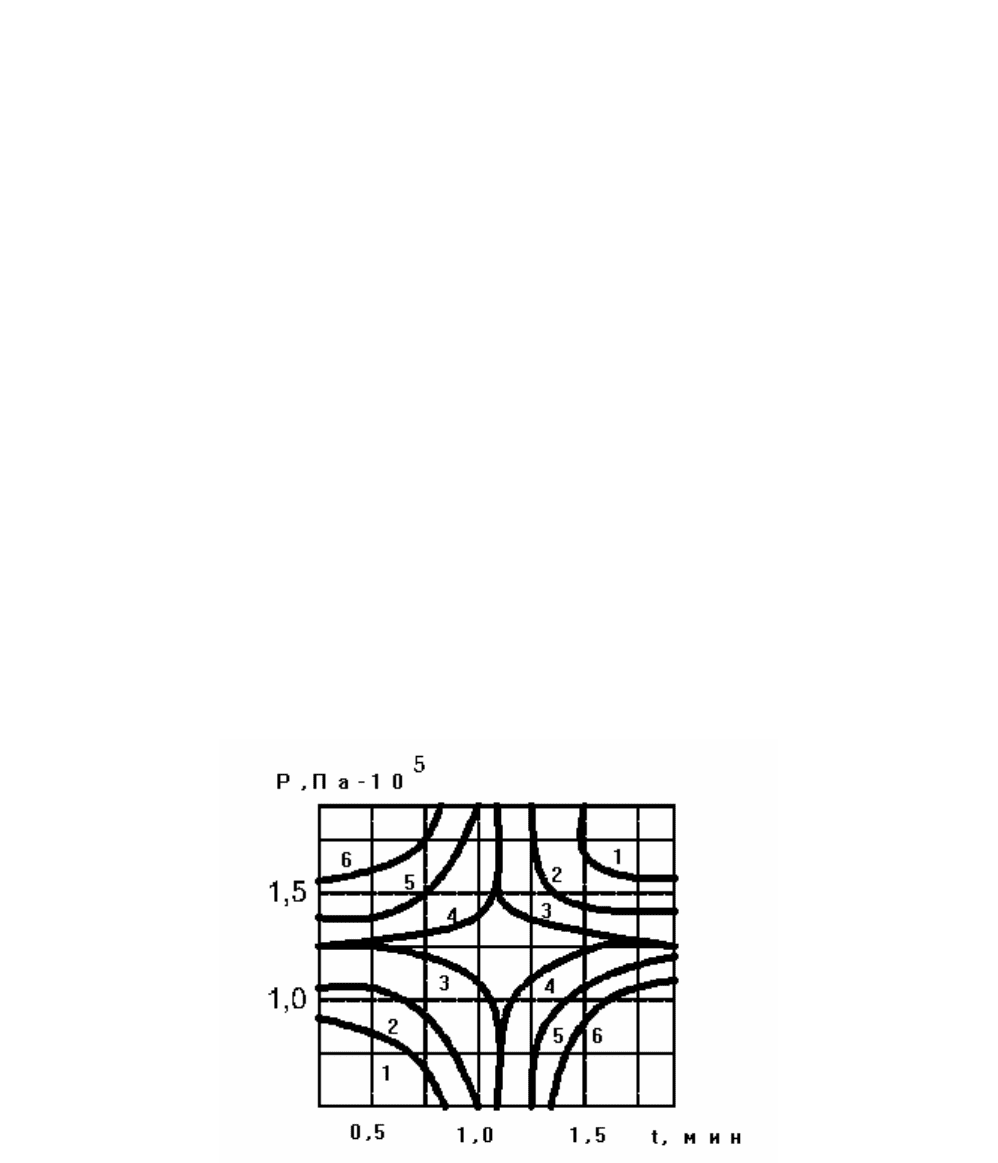
Геометрическая интерпретация представлена на рисунке 7. По.
координатным осям отложены в размерном выражении время обработки t и
давление пара P. Значении функции отклика .(в миллиграммах пептина на 1 г в
час) отложены в виде семейства кривых: 1 - 160; 2 - 180; 3-185; 4 - 187; 5 - 190; 6 -
200.
Эти кривые имеют вид равнобочных гипербол с асимптотами, которые
совпадают по направлению с координатными осями. Геометрический анализ
кривых показывает, что между значениями функции отклика 185 и 187 они
должны выродиться в точку. Эта особая точка называется минимаксом. В ней
пересекаются асимптоты, делящие координатное поле на квадранты с разными
свойствами (в I и III при удалении от минимакса функция отклика уменьшается,
во II и IV – растет).
Выбор II или IV квадранта для оптимизации процесса гидротермической
обработки в данном случае должен быть определен из условий оптимальности
другого (дополнительного) критерия - товарного (кулинарного) качества рисовой
крупы. Поскольку с увеличением t и уменьшением р (IV квадрант) не происходит
ухудшения цвета крупы, который является основным показателем. товарного
качества, оптимум следует искать именно в этом квадранте.
Рисунок 7 – Параметрическая диаграмма
Второй способ анализа результатов с помощью аксонометрических
построений позволяет определить оптимальную область проведения
эксперимента с помощью максимума или минимума на поверхности отклика или
на проекции линий равного уровня, рисунок 6.
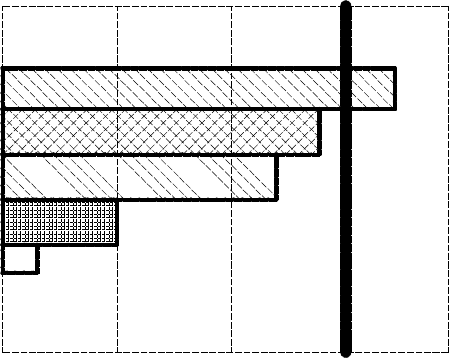
Значимость коэффициентов модели определяют также при помощи карты
Парето. Карта позволяет оценить значимость коэффициентов, а соответственно и
степень влияния факторов на выходной параметр Y. Карта Парето представляет
собой гистограмму, пример представлен на рисунке 8.
38
Рисунок 8 – Карта Парето
5.4 Алгоритм реализации ПФЭ 2
3
1. В соответствии с заданием из приложения 4 строится матрица
планирования.
2. Производится усреднение значений выходного параметра Y по формуле
(38).
3. Находятся оценки дисперсий по формуле (39).
4. Определяется расчетное значение критерия Кохрена по формуле (40).
Делается вывод об однородности дисперсий.
5. Определяется дисперсия воспроизводимости по формуле (40).
6. Определяются коэффициенты математической модели (41).
7. Определяется значимость коэффициентов математической модели при
помощи формулы (45).
8. Составляется математическая модель с учетом только значимых
коэффициентов.
9. Определяется среднеквадратическая ошибка S
bi
(44).
10. Рассчитывается дисперсия адекватности S
ад
(46).
11. Определяется критерий Фишера (47). Делается вывод об адекватности
математической модели.
12. Определяется работоспособность адекватной модели (14).
13. Осуществляется построение ПФЭ 2
3
в пакете Statgraphics Plus.
14. Производится анализ математической модели и результатов
эксперимента.
Задания по данной теме находятся в приложении Г.
39
6 СТАТИСТИЧЕСКИЕ ИГРЫ. КРИТЕРИИ ПРИНЯТИЯ
РЕШЕНИЯ
Управление производственными процессами осуществляется путем
реализации последовательности принимаемых решений. Для этого необходима
информация о состоянии объекта управления в условиях его работы. В случае
отсутствия достаточно полной информации возникает неопределенность в
принятии решения.
Любую хозяйственную деятельность можно рассматривать как игру с
природой. В широком смысле под «природой» будем понимать совокупность
неопределенных факторов, влияющих на эффективность принимаемого
решения.
Статистические игры представляют собой основную модель теории
принятия решений в условиях частичной неопределенности.
Множество состояний природы обозначим через П, отдельное состояние
через П
j
, П
j
∈ П (j=1, n). Множество решений (стратегий) обозначим через А,
отдельное решение – A
i
, A
i
∈A (i=1, m).
Во взаимоотношениях с природой можно использовать любые стратегии из
А в зависимости от состояний природы П
j
. Имея ряд стратегий А
1
, …, А
m
статистик может руководствоваться некоторым правилом поведения с помощью
которого он определяет какую стратегию ему выбрать. Иными словами, статистик
отыскивает оптимальное поведение, которое и будет является оптимальной
стратегией.
Чтобы выразить в количественной форме упомянутое выше правило,
которым статистик должен руководствоваться, предполагается, что есть
возможность численно оценить величиной a
ij
эффективность каждой комбинации
(A
i
;П
j
), иначе говоря, качество решения A
i
.
Тем самым будет определена так называемая платежная матрица
статистической игры на основе, которой в дальнейшем и будут сформулированы
критерии выбора оптимальной стратегии.
Элемент a
ij
назовем выигрышем статистика, если он использует стратегию
A
i
при состоянии природы П
j
.
Оптимальную стратегию можно определить, используя ряд критериев. Так,
при известном распределении вероятностей различных состояний природы Пj
пользуются критерием Байеса. Показателем в этом критерии служит либо
величина среднего выигрыша, либо величина среднего риска.
Составляется платежная матрица, которая имеет вид:
mnmm
n
n
aaa
aaa
aaa
...
............
...
...
21
22221
11211
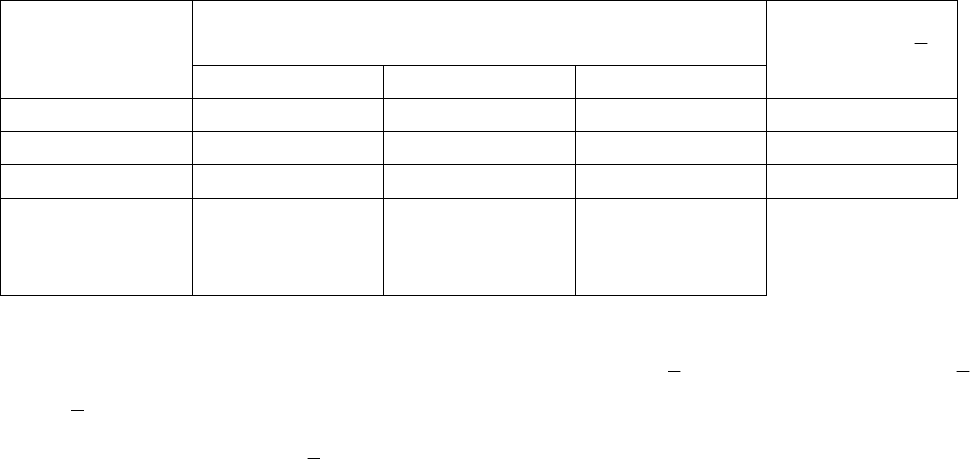
40
Таблица 10 – Платежная матрица
Варианты возможных решений (или
состояния природы)
Стратегия
статистика
A
i
П
1
П
2
П
3
Средний
выигрыш
i
a
A
1
-a
11
-a
12
-a
13
A
2
-a
21
-a
22
-a
23
A
3
-a
31
-a
32
-a
33
Вероятность
данных
событий q
j
q
1
q
2
q
3
Значения a
11
, a
12
и т.д. в платежную матрицу вносятся с коэффициентом –1.
По критерию Байеса за оптимальную принимается та чистая стратегия Ai,
при которой максимизируется средний выигрыш
i
a , т.е. обеспечивается
i
a =
max
i
a , где
∑
=
==
n
j
jiji
miqaa
1
),1(
(48)
По критерию Вальда за оптимальную принимается чистая стратегия А
i
, при
которой наименьший выигрыш игрока будет максимальным, т.е. ему
обеспечивается
α = max
i
min
j
a
ij
В таблицу 10 добавляется еще один столбец α
i
, в который вносятся минимальные
элементы строк по каждой стратегии A
i
.
Поэтому оптимальной по Вальду будет стратегия:
α=max
i
min
j
a
ij
=max
i
α
i
Критерий Вальда выражает позицию крайнего пессимизма, и принимаемое
решение носит заведомо перестраховочный характер.
При выборе оптимальной стратегии игрока А опираются как на платежную
матрицу, так и на матрицу рисков. Риском r
ij
игрока А, когда он пользуется чистой
стратегией А
i
при состоянии природы П
j
, называют разность между
максимальным выигрышем, который он мог бы получить, если бы достоверно
знал, что природой будет реализовано именно состояние П
j
, и тем выигрышем,
который он получит, используя стратегию А
i
в неведении о том, какое же
состояние П
j
природа реализует. Таким образом, элементы матрицы r
ij
матрицы
рисков определяются по формуле r
ij
= β
j
-a
ij
≥ 0, где β
j
= max a
ij
- максимально
возможный выигрыш игрока А при состоянии П
j
(максимальный элемент j-го
столбца платежной матрицы).
