Кошак Ж.В, Минина Е.М. Применение ЭВМ в отрасли

Подождите немного. Документ загружается.

6) коэффициенты при двойственных переменных в целевой функции ДЗ

равны правым частям ограничений исходной задачи;

7) максимизация целевой функции исходной задачи заменяется

минимизацией целевой функции в ДЗ.

Например, исходная задача линейного программирования имеет вид:











≤++

→++=

25357

162

max954

321

xxx

xxxЦФ

Двойственная задача на основе вышеизложенных указаний будет иметь вид:











=≥

≥+

→+=

2,1;0

932

min2516

yyЦФ

В общем виде ДЗ имеет вид:











≥

→=

∑

min

jiij

iiД

cya

ybЦФ

Важное свойство двойственной задачи заключается в том, что max ЦФ =

min ЦФ

Двойственная переменная y

является коэффициентом при b

и,

следовательно, показывает, как изменяется ЦФ при изменении ресурса b

на

единицу. Двойственные переменные называют двойственными оценками. В

электронных таблицах Excel двойственная оценка называется теневой ценой.

Существенным является то, что для нахождения двойственных оценок решать

двойственную задачу не требуется. Их значения уже находятся в симплексной

таблице оптимального решения исходной задачи.

Если некоторый i-ый ресурс используется не полностью, т.е. имеется

резерв, значит, дополнительная переменная в ограничении для данного

ресурса будет больше нуля, а двойственная оценка этого ограничения

равна нулю.

В двойственную задачу для перехода от неравенств к равенствам

вводятся дополнительные двойственные переменные. Смысл дополнительных

двойственных переменных заключается в следующем: если основные

переменные (например, х

, х

) вошли в оптимальное решение, то

дополнительные переменные (y

, y

) равны нулю. Если основные

переменные не вошли в оптимальное решение, т.е. равны нулю, то

соответствующие им дополнительные переменные имеют положительное

значение. Дополнительные переменные двойственной задачи показывают

насколько уменьшиться значение целевой функции при принудительном

выпуске единицы данной продукции.

Например, оптимальный опорный план задачи о наилучшем

использовании ресурсов представлен в таблице 5.

Таблица 5 – Оптимальный опорный план

X1 X2 X3 X4 X5 X6 X7

БП СБ А

140

160

x5 0

56,667

0,0136667

0,003

-0,66667

x3 160

9166,7

1,25

1,1666667

0,5

83,33333

x2 0

-0,0015

0,003

0,009

-0,5

ЦФ

-C

1E+06

170

46,666667

13333,33

При анализе оптимального опорного плана устанавливается соответствие

между прямыми переменными и переменными двойственной задачи, в данном

примере соответствие будет выглядеть следующим образом:

БП СБ

Оптимальный план двойственной задачи следующий:

Y*= (0; 13333,33; 0; 170; 46,7; 0; 60)

Анализируя оптимальный план двойственной задачи получается, что

*>0 – ресурсы второго вида используются полностью. Y

*=0 и y

*=0 ресурсы

первого и третьего вида используются полностью. Y

*=170, y

*=60 при

выпуске продукции первого и четвертого вида, не вошедшей в оптимальный

план уровень прибыли будет снижаться на данные величины y

* и y

3.5 Реализация симплексного метода с помощью Поиска

решения в электронных таблицах Excel

Данный способ решения наиболее удобный и быстрый. Для реализации

симплексного метода с помощью Поиска решения в электронных таблицах

Excel необходимо создать электронную форму, которая является шаблоном для

решения задачи о наилучшем использовании ресурсов. Вид формы

представлен на рисунке 4.

Рисунок 4 - Форма для расчета с помощью Поиска решения

321

765

yyy

xxx

ccc

7654

4321

yyyy

xxxx

cccc

В строку «Коэффициенты в целевую функцию» вводятся данные строки

Прибыль из варианта задания (Приложение Б).

В «Ограничения» вносится расход соответствующего ресурса на единицу

продукции.

В столбец «Правая часть» заносятся значения столбца «Наличие» из

варианта задания.

В ячейку ЦФ F6 вводится зависимость для целевой функции.

1). Вызывается Мастер функций. Выбирается категория Математические,

функция СУММПРОИЗВ.

2). В открывшемся диалоговом окне в строке массив 1 вводится диапазон

B3:E3, рисунок 4.

3). В строку массив 2 вводится диапазон B6:E6.

4). Нажимается кнопка Готово.

В ячейки F9, F10, F11, которые рассчитывают расход каждого ресурса при

выпуске всех видов продукции, вводятся зависимости для левых частей

ограничений. Для этого:

1) копируется содержимое ячейки F6 (ЦФ) в ячейку F9, F10, F11;

2) В ячейке F9 редактируется формула и принимает следующий вид: =

СУММПРОИЗВ(B$3:E$3;B9:E9);

3) В ячейке F10 редактируется формула и принимает следующий вид: =

СУММПРОИЗВ(B$3:E$3;B10:E10);

4) В ячейке F11 редактируется формула и принимает следующий вид: =

СУММПРОИЗВ(B$3:E$3;B11:E11);

На этом ввод данных в форму закончен.

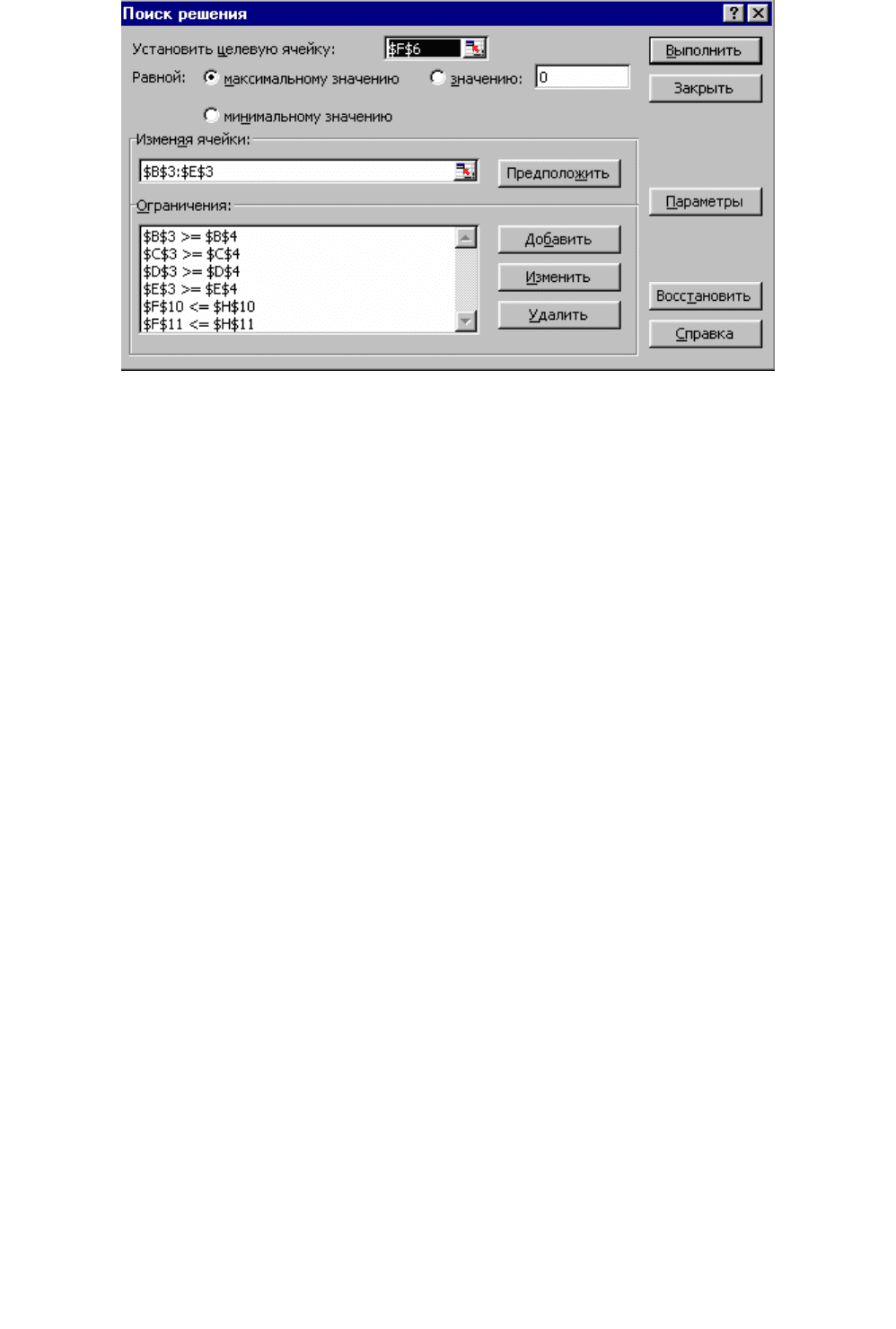
1. Выбрать меню Сервис, команду Поиск решения.

2. На экране отобразиться окно Поиск решения (рисунок 5). В строке

«Установить Целевую ячейку» указывается ячейка $F$6 – ячейка ЦФ. Установить

маркер напротив Равной Максимальному значению.

3. В поле Изменяя ячейки указать диапазон $B$3:$E$3.

4. В поле Ограничения вводятся ограничения для расчета Целевой

функции. Для этого нажимается кнопка Добавить и в появившемся окне вводятся

следующие ограничения: $B$3>=$B$4; $C$3>=$C$4; $D$3>=$D$4; $E$3>=$E$4;

$F$9<=$H$9; $F$10<=$H$10; $F$11<=$H$11. После ввода последнего

ограничения вместо кнопки Добавить нажимается кнопка ОК.

5. На экране появится диалоговое окно с введенными условиями.

6. Нажимается кнопка Параметры.

7. В появившемся диалоговом окне вводятся параметры поиска решения, а

именно в поле Максимальное время вводится 100 секунд; предельное число

итераций – 100, относительная погрешность – 0,000001; допустимое отклонение 5

%. Устанавливается галочка напротив команды Линейная модель. В поле Оценка

устанавливается маркер напротив команды Линейная. В поле Производные

устанавливается маркер напротив команды Прямые. В поле Метод

устанавливается маркер напротив команды Ньютона. Нажимается кнопка ОК.

Рисунок 5 – Окно поиска решения

После выполнения всех этих операций в форме отобразится результат

поиска решения.

3.6 Алгоритм решения задачи о наилучшем использовании

ресурсов

1. Составляется математическая модель задачи.

2. Математическая модель приводится к каноническому виду.

Преобразование состоит в переходе от системы неравенств к равенствам. Для

этого вводятся дополнительные переменные в каждое уравнение ограничений.

3. Составляется начальный опорный план.

4. Определяется оптимальность начального опорного плана.

5. При неоптимальности начального опорного плана строится новый

опорный план. Для этого используются преобразования п. 3.3.

6. Определяется оптимальность нового опорного плана.

7. При нахождении оптимального решения строится двойственная задача и

решается в соответствии с п. 3.4.

8. Проверка правильности решения проводится при помощи Поиска

решения, п. 3.5.

Задания по данной теме находятся в приложении Б.

4 СТАТИСТИЧЕСКИЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Статистический дисперсионный анализ — один из методов выявления

влияния отдельных факторов на показатель технологического процесса, или

параметр оптимизации, вместе с регрессионным и корреляционным анализом

составляет основу обработки экспериментальных данных, полученных в

результате пассивного и активного экспериментов.

В данном случае при дисперсионном анализе имеют дело с дисперсиями

факторов, т. е. мерой разброса измеренных значений переменного относительно

средней величины.

В общем виде задачи дисперсионного анализа могут быть сформулированы

следующим образом. Текущий контроль или специальные исследования

производства устанавливают неустойчивость того или иного процесса либо

качества продукта. Вместе с тем, данные контроля не указывают непосредственно

на главную причину этой неустойчивости. Как проанализировать эти данные,

чтобы с требуемой достоверностью определить влияние каждого из факторов на

колеблемость или изменчивость изучаемого показателя?

Эта же задача может быть поставлена и в несколько иной форме. Характер

колебаний рассматриваемого признака относительно устойчив, однако размах

колебаний гораздо больше допустимого или желательного. Необходимо

уменьшить размах и выявить для этого, какую долю размаха вызывает тот или

другой из известных факторов процесса.

Метод решения таких задач — дисперсионный анализ — основан на

свойстве аддитивности дисперсии, т. е. на том, что полная дисперсия

интересующего нас показателя равна сумме составляющих ее частных дисперсий.

Простейшим случаем дисперсионного анализа является однофакторный

дисперсионный анализ. Если регрессионный анализ позволяет осуществить

количественный анализ данных, то дисперсионный анализ осуществляет их

качественный анализ. Под факторами будем понимать различные независимые

показатели. Термин однофакторный анализ или классификация по одному

признаку относиться к анализу, который сравнивает средние арифметические

результативного признака, получаемые при различных уровнях фактора.

Исследуемый результативный признак Y – случайная величина, зависящая

от одного фактора X. Фактор X изучается на m уровнях X

, X

,…X

и на каждом

уровне фактора X приведено одинаковое число измерений n признака Y. Данные

представляются в виде таблицы 6

Таблица 6

Уровни фактора X Номер

испытания

… X

1 Y

… Y

2 Y

… Y

… … … … … … …

n Y

… Y

Групповое

среднее

…

В последней строке таблицы 6 вычисляются групповые средние значения y

полученных наблюдений для каждого из уровней фактора:

mjy

ijj

,1,

∑

(27)

Для решения задач дисперсионного анализа вычисляются следующие

величины:

1) общее выборочное среднее

признака Y

∑∑∑

===

jij

111

(28)

2) общую сумму квадратов отклонений полученных наблюдений от

общего среднего y

∑∑

−=

общ

yySS

)(

(29)

3) факторную сумму квадратов отклонений групповых средних y

от

общего среднего y

)()( yynyySS

факт

−=−=

∑∑∑

===

(30)

Факторная сумма квадратов отклонений характеризует разброс значений

уровней фактора относительно общего выборочного среднего, т.е. между

уровнями фактора.

4) остаточную сумму квадратов отклонений значений y

от своей

групповой средней

∑∑

−=

jij

ост

yySS

)(

(31)

Наличие разброса при фиксированном значении фактора х объясняется

действием неучитываемых факторов, т. е. различными случайными причинами.

Не выделяя какую-либо одну из них, будем характеризовать суммарный эффект

от них остаточной дисперсией S

ост

, которая, представляя разброс результатов

измерений у относительно у

iср

зависит от суммы квадратов отклонений у,

измеренных при каждом значении х, от соответствующих условных групповых

средних

y .

Очевидно, что если исключить влияние неучитываемых факторов, разброса

у при фиксированном x наблюдаться не будет и общий разброс у определится

только действием х. С другой стороны, если бы влияние фактора х на у

отсутствовало, а случайные причины оказывали свое действие, то общий разброс

у определялся бы только ими и характеризовался только остаточной дисперсией

от действия неучитываемых факторов.

Поэтому правильность вычислений проверяется из условия:

общ

= SS

факт

+ SS

ост

На основе полученных значений квадратов отклонений вычисляется общая,

факторная и остаточная дисперсии. Для этого суммы квадратов отклонений

нужно разделить на соответствующее количество степеней свободы:

)(

общ

−

∑∑

(32)

)(

факт

−

∑∑

(33)

∑∑

−

jij

ост

)(

)1(

(34)

Для проверки влияния уровней факторов на показатель изучаемого процесса

воспользуемся критерием Фишера. Вычисляется F-отношение, т. е. отношение

ост

факт

F =

(35)

если S

факт

< S

ост

или

факт

ост

F =

(36)

если S

ост

< S

факт.

По уровню значимости α=0,05 и числу степеней свободы к

и к

, где к

число степеней свободы большей дисперсии, найдем границу критической

области

=F(α,к

, к

Если F

эксп

< F

крит

, то Н

принимается, то есть влияние фактора Х признается

несущественным.

Если же F

эксп

> F

крит

, то Н

отвергается, влияние фактора Х на признак У

признается существенным. В этом случаи задача дисперсионного анализа может

быть продолжена с использованием положений регрессионно-корреляционного

анализа.

4.1 Реализация дисперсионного анализа с помощью анализа

данных в электронных таблицах Excel

Анализ данных в электронных таблицах позволяет быстро провести

однофакторный и двухфакторный дисперсионный анализ.

Для проведения однофакторного дисперсионного анализа необходимо

выполнить следующую последовательность действий:

1. Разместить исходные данные в таблицу 6.

2. Вызвать меню Сервис команду Анализ данных.

3. В открывшемся диалоговом окне выбрать Однофакторный дисперсионный

анализ.

4. В диалоговом окне «Однофакторный дисперсионный анализ» указать

диапазон размещения исходных данных, установить маркер напротив команды

Группировать по столбцам, указать начальную ячейку диапазона, где будет

размещаться результат.

4.2 Алгоритм реализации однофакторного дисперсионного

анализа

o Данные для дисперсионного анализа заносятся в таблицу 6.

o Рассчитывается групповое среднее по формуле (27)

o Рассчитывается общее выборочное среднее по формуле (28)

o Для расчета общей суммы квадратов отклонений составляется таблица 7.

Таблица 7

№ y

)

…

сумма

o Общая сумма квадратов отклонений рассчитывается по формуле (29).

Значения для расчета берутся из таблицы 7.

o Рассчитывается факторная сумма квадратов отклонений по формуле

(30).

o Для расчета остаточную сумму квадратов отклонений составляется

вспомогательная таблица 8.

Таблица 8

№ y

y )

…

сумма

o Рассчитывается остаточная сумма квадратов отклонений по формуле

(31).

o Рассчитывается общая дисперсия по формуле (32).

o Рассчитывается факторная дисперсия по формуле (33).

o Рассчитывается остаточная дисперсия по формуле (34)

o Рассчитывается F-отношение.

o По таблицам Фишера определяется F

крит

o Сравнивается F-отношение с F

крит

и делается вывод о степени влияния

уровней фактора на признак y.

Задания по теме «Статистический дисперсионный анализ» в приложении В.

5 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА

Планирование эксперимента позволяет экспериментатору, пользуясь

математическими методами, целенаправленно изменять условия опытов.

Основываясь на имеющихся сведениях об изучаемом процессе, исследователь

выбирает некоторую оптимальную методику для управления экспериментом.

Процесс исследования обычно разбивается на отдельные этапы. После каждого

этапа исследователь получает новую информацию, позволяющую ему изменять

методику исследования.

Задача всего исследования формулируется следующим образом: нужно

получить представление о функции отклика у=ϕ(х

, X

, ..., х

) (где у—параметр

процесса, подлежащий оптимизации; x

, x

..... х

— независимые переменные —

факторы, которые можно варьировать при постановке экспериментов).

Координатное пространство с координатами х

, x

,…, х

называется

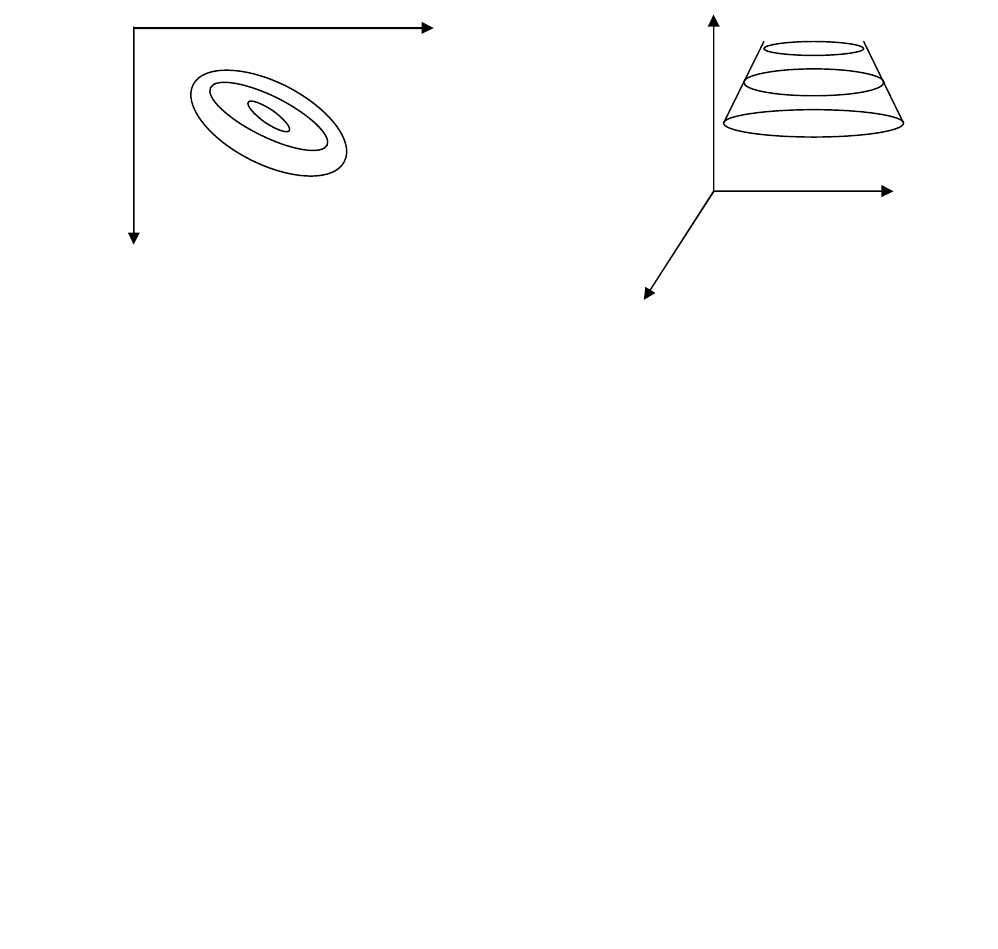
факторным пространством, а геометрический образ, соответствующий функции

отклика, называется поверхностью отклика, представленной на рисунке 6б.

а б

Рисунок 6 – Поверхность отклика

При двух факторах поверхность отклика можно изобразить в виде проекций

линий равного уровня на плоскость X

, представленной на рисунке 6а.

Задача планирования эксперимента формулируется так: на каждом

этапе исследования нужно выбрать оптимальное расположение точек в

факторном пространстве для того, чтобы получить некоторое представление

о поверхности отклика. Оптимальность расположения точек определяется

целью, к которой стремится экспериментатор на данном этапе.

Активный эксперимент можно назвать дважды оптимальным: он определяет

наилучшее соотношение независимых факторов для проведения

технологического процесса, а методы проведения самого эксперимента

оптимальны в том смысле, что позволяют решить задачу с минимальными

затратами времени и средств. Тем не менее, существует другое название —

экстремальные эксперименты, хотя экстремум далеко не всегда является

оптимумом. Это название принято в статистике по традиции: к экстремальным

задачам относят задачи отыскания максимумов и минимумов функции, если они

являются оптимальными значениями.

Прежде чем заняться построением функции отклика, необходимо решить

вопрос о том, сколько и какие факторы следует принять в рассмотрение, а также

провести так называемые отсеивающие эксперименты, цель которых —

выделить доминирующие факторы среди большого числа возможных. После

определения доминирующих факторов необходимо приступить непосредственно

к эксперименту.

5.1 Полный факторный эксперимент (ПФЭ). ПФЭ 2

Математическая модель технологического процесса, которую необходимо

оптимизировать с помощью активного эксперимента; представляет собой

уравнение регрессии. Чтобы получить независимые оценки - коэффициенты этого

уравнения, нужно предъявить к фиксированным значениям независимых

переменных некоторые требования. Таблица значений или уровней факторов при

проведении каждого опыта (в дальнейшем будем называть ее матрицей

планирования) должна иметь линейно независимые столбцы, а сумма

произведений значений любых двух факторов, т. е. чисел двух столбцов, должна

равняться нулю. Такую матрицу, называемую ортогональной, имеет полный

факторный эксперимент.

Перед началом опытов на основании априорных данных выбирается

технологический режим, который является базовым. Математическое описание

объекта в окрестности точки базового режима х

может быть получено

варьированием каждого из факторов Xi на двух уровнях, отличающихся от

базового уровня на величину шага варьирования ±∆x

. Факторы должны быть

независимые, т, е. допускать изменение любого из них на некоторую величину без

изменения при этом всех других факторов.

Шаг варьирования по каждой переменной выбирается таким, чтобы

приращение величины выходного параметра Y к базовому значению при

реализации шага можно было выделить на фоне «шума» при небольшом числе

параллельных опытов. Шаг варьирования не должен быть ни слишком маленьким

(не менее погрешности измерения фактора), ни слишком большим. Доля шага или

интервала варьирования для всей области возможных значений данного фактора

выбирается в зависимости от конкретных условий каждого этапа эксперимента.

Полным факторным экспериментом (ПФЭ) можно считать эксперимент,

реализующий все возможные не повторяющиеся комбинации уровней

независимых переменных, каждый из которых принудительно (активно)

варьируется на двух уровнях. Число этих комбинаций при n факторах равно N=2

и определяет тип планирования.

В дальнейшим рассмотрим планирование типа N=2

, т. е. на примере

объекта с тремя факторами х

, x

При планировании эксперимента проводят преобразование (нормализацию)

независимых переменных x

; с помощью безразмерных переменных z

= (x

—

)/∆x

, что дает возможность легко построить ортогональную матрицу

планирования и облегчает дальнейшие расчеты, так как верхний и нижний

уровни варьирования (z

iверх

когда х

<х

, и z

iнижн

, когда х

>х

) равны

соответственно + 1 и -1.

Для трехфакторной задачи нормализованное уравнение регрессии имеет вид