Кошак Ж.В, Минина Е.М. Применение ЭВМ в отрасли

Подождите немного. Документ загружается.

Y=f(X)

r = 0

-50

-40

-30

-20

-10

012345678

в)

Y=f(X)

y = 2,8214x + 1,8571

r = 0,917

0510

г)

Рисунок 1

Чем ближе коэффициент корреляции к единице, тем теснее линейная

зависимость между случайными переменными X и Y. Коэффициент корреляции

определяется по формуле:

∑∑∑∑

∑

−⋅⋅−⋅

⋅

−

⋅

)()(

iiii

yynxxn

yxyxn

(15)

2.4 Дисперсионный анализ

Для проверки соответствия линейной регрессионной модели

экспериментальным данным используют метод однофакторного дисперсионного

анализа.

Для этого рассчитывается:

1 полную сумму квадратов (общую дисперсию):

∑

−=

)( yya

(16)

2 сумму квадратов регрессии:

)(

∑

−= yyb

расч

(17)

3 остаточную сумму квадратов

)(

∑

−=

расчi

yyc

(18)

Проверяется a=b+c.

Проверяется гипотезу линейности , т.е. нулевую гипотезу вида H

: ρ=0 против

альтернативной гипотезы H

: ρ

<>0.

Для удобства вычислений составляется таблица дисперсионного анализа:

Таблица 3

Источник

изменчивости

Суммы

квадратов

Число

степеней

свободы

Средние

квадраты

набл

Линейная

регрессия

b 1 М1 = b

Остаток c n-2 М2 = c/(n-2)

Полная

изменчивость

a n-1

=М1/М2

Если нулевая гипотеза верна, то выборочная статистика F имеет распределение

Фишера с υ

=1 и υ

=n-2 степенями свободы.

Гипотеза отсутствия линейной связи между переменными X и Y отвергается на

основании этой статистики, если вычисленное значение F

набл

> F

α,1,n-2

– это квантиль F-распределения с υ

=1 и υ

=n-2 степенями свободы. В

противном случае гипотеза отсутствия линейной связи между переменными X

и Y считается согласующейся с данными эксперимента.

2.5 Алгоритм регрессионно-корреляционного анализа

1. Строится корреляционное поле.

2. Найти коэффициенты уравнения регрессии методом наименьших

квадратов.

3. Найти несмещенную дисперсию и среднеквадратичные ошибки S

и S

4. Построить 95 %-ый доверительный интервал для коэффициентов

уравнения регрессии.

5. Найти коэффициент корреляции.

6. Вычислить статистику t

набл

7. Определить коэффициент детерминации R

8. Провести дисперсионный анализ.

2.6 Реализация методов с помощью анализа данных в

электронных таблицах Excel

Анализ данных электронных таблиц Excel позволяет автоматически

осуществить поиск коэффициентов уравнения регрессии и определение

коэффициентов корреляции, детерминации, доверительных интервалов и т.д.

Для этого необходимо выполнить последовательно следующие действия:

1 Выбирается меню Сервис, команда Анализ данных.

2 В открывшемся окне Анализ данных выбирается команда Регрессия.

3 В окне Регрессия в строке Входной интервал Y указывается диапазон, где

размещаются исходные значения Y в электронной таблице.

4 В строке Входной интервал X указывается диапазон размещения

исходных значений X в электронной таблице.

5 В Параметрах вывода в окне Регрессия указывается, где Вы хотите

расположить результат: на этом же листе, на новом листе или в новой книге.

После выбора места расположения указывается диапазон, в котором будут

располагаться результаты вычислений.

6 В команде Остатки указывается, какие остатки необходимо вывести

после вычислений, например вывод Стандартизированных остатков и Остатков.

Для этого напротив этих команд устанавливаются галочки.

7 В команде Нормальная вероятность установить галочку напротив

команды График нормальной вероятности и график подбора.

2.7 Подбор уравнения регрессии при помощи линий тренда в

электронных таблицах Excel

Для построения линий тренда необходимо:

1 Выделить точку на корреляционном поле и вызвать контекстное меню, в

котором выбирается команда Добавить линию тренда;

2 В открывшемся диалоговом окне Линия тренда представлены шесть видов

линий тренда. Выбирается линия тренда наиболее соответствующая

расположению точек на корреляционном поле;

3 Во вкладке Параметры диалогового окна Линия тренда устанавливаются

флажки напротив команд Показать уравнение на диаграмме и Поместить на

диаграмму величину достоверности аппроксимации R

. Величина

достоверности аппроксимации – это коэффициент детерминации. Нажимается

кнопка ОК. После чего на графике отображается уравнение регрессии и значение

коэффициента детерминации.

Наиболее соответствует экспериментальным данным та линия тренда,

коэффициент детерминации которой наибольший и наиболее близок к единице.

При этом коэффициент детерминации должен быть больше 0,7.

2.8 Реализация метода наименьших квадратов средствами

MathCAD

Линейная регрессия является самым простым и в то же время наиболее

часто используемым типом регрессии. Классическим алгоритмом линейной

регрессии является метод наименьших квадратов, идея которого сводится к

поиску таких коэффициентов для уравнения прямой, чтобы сумма квадратов

абсолютных ошибок (b-ax

-y

) была минимальна.

В MathCAD этот метод основной. Рассчитать линейную регрессию в

MathCAD по методу наименьших квадратов можно с помощью двух

альтернативных способов.

Первый, более простой, использует специальную функцию line(x,y), где x и

y – соответствующие вектора экспериментальных данных. Результатом работы

этой функции является вектор, первый элемент которого отвечает коэффициенту

b, второй – коэффициенту a уравнения, наиболее хорошо усредняющей выборку

прямой (функция прямой имеет общий вид f(x)=аx+b).

Недостатком функции line – результат она выдает в виде одного вектора,

что не всегда удобно.

В MathCAD существуют функции, позволяющие вычислить коэффициенты

уравнения линейной регрессии по отдельности:

Intercept(x,y). Определяет значение коэффициента b (что соответствует первой

строке результата функции line);

Slope (x,y) – находит величину коэффициента a (равняется второму элементу

ответа функции line.

Алгоритм реализации метода наименьших квадратов в MathCAD:

1 Ввести значения x и y в векторной форме.

Для этого записывается выражение x:=.

После чего на панели инструментов Math выбираем кнопку с изображением

матрицы. В появившемся диалоговом окне в строке количество строк указываем

число, соответствующее количеству значений х, а строке количество столбцов

значение 1.

На экране отобразится столбцовая матрица, которую необходимо заполнить

значениями х.

Аналогичным образом заполняем и матрицу y.

Матрицы такого вида в MathCAD называются векторами.

2 Ниже располагаем функцию line(x,y). Блок вычислений этой функции

должен выглядеть следующим образом:

Rlinexy,():= R

81.945

0.71−













4 Строим график получившейся функции. Для этого записываем уравнение в

следующем виде:

rz()zR

⋅ R

+:=

После чего выбирается панель инструментов Graph. На которой выбирается

кнопка с требуемым типом диаграммы. После этого отображается пустая

координатная плоскость выбранной диаграммы и в нее вносятся названия осей.

На рисунке 2 представлен результат построения линии регрессии.

10 505101520

89.047

70.5

rz()

17.610− xz,

Рисунок 2

Задания по регрессионно-корреляционному анализу в приложении А.

3 ПОИСКОВАЯ ОПТИМИЗАЦИЯ

3.1 Понятие линейного программирования

Линейное программирование – раздел математического программирования,

применяемый при разработке методов отыскания экстремума линейных функций

нескольких переменных при линейных дополнительных ограничениях,

налагаемых на переменные. По типу решаемых задач его методы разделяют на

универсальные и специальные. С помощью универсальных методов могут

решаться любые задачи линейного программирования. Специальные методы

учитывают особенности модели задачи, ее целевой функции и системы

ограничений.

Особенностью задач линейного программирования является то, что

экстремума целевая функция достигает на границе области допустимых значений.

С помощью линейного программирования решаются следующие типы

задач: задача о наилучшем использовании ресурсов, задача о выборе

оптимальных технологий, задача о раскрое материала, транспортная задача,

задача о смесях и т.п.

3.2 Типы задач, решаемые методами линейного

программирования

3.2.1 Задача о наилучшем использовании ресурсов

Пусть некоторая производственная единица (цех, завод, объединение и т.д.)

исходя их конъюнктуры рынка, технических и технологических возможностей и

имеющихся ресурсов может выпускать N различных видов продукции (Прод1,

Прод2,…Продn). Предприятие при производстве этих видов продукции должно

ограничиваться имеющимися видами ресурсов, технологий и других

производственных факторов. Все эти виды ограничивающих факторов называют

ингредиентами R

. Пусть их число равно m. Они ограничены, и их количества

равны соответственно b

, b

…b

условных единиц. Таким образом b=(b

;

;…;b

;…b

) – вектор ресурсов. Известна экономическая выгода (мера

полезности) производства продукции каждого вида, исчисляемая по различным

факторам (по отпускной цене товара, его прибыльности, издержкам производства,

степени удовлетворения потребностей и т.п.). Примем в качестве такой меры,

цену реализации с

. Вектор цен с=(с

; с

;…;c

). Известны также

технологические коэффициенты a

, которые указывают, сколько единиц i-го

ресурса требуется для производства продукции j вида. Матрицу коэффициентов a

называют технологической и обозначают буквой А. Имеем A=[a

Обозначим через х = (х

;…;x

) план производства, показывающий,

какие виды товаров Прод

, Прод

…, Прод

нужно производить и в каких

количествах, чтобы обеспечить предприятию максимум объема реализации при

имеющихся ресурсах.

Тогда общий объем реализации будет следующий:

ЦФ=с

+…с

Это выражение – целевая функция, которую нужно максимизировать.

Так как a

расход i-го ресурса на производство xj единиц j-той продукции,

то, просуммировав расход i-го ресурса на выпуск всех N видов продукции,

получим общий расход этого ресурса, который не должен превосходить bi

единиц:

+…+a

<=b

Чтобы искомый план х=(х

;х

;…;xj;…;x

) был реализован наряду с

ограничениями на ресурсы нужно наложить условие неотрицательности на

объемы xj выпуска продукции:

>=0 (j=1,N)

Таким образом, математическая модель задачи о наилучшем использовании

ресурсов имеет вид:

Найти:

(19)

При ограничениях:

(20)

3.2.2 Задача о выборе оптимальных технологий

В задаче о наилучшем использовании ресурсов определяется оптимальный

план выпуска продукции. Пусть при производстве какого-либо продукта

используется n технологий. При этом требуется m видов ресурсов, заданных

объемами b

(i=1,m). Эффективности технологий, т.е. количество конечной

продукции (в рублях), производимой в единицу времени по j-той технологии

(j=1,n), обозначим c

. Пусть a

– расход i-го ресурса в единицу вресени по j-той

технологии. Пренебрегая временем переналадок, необходимым для перехода от

одной технологии к другой, получаем следующую математическую модель

задачи: найти план интенсивностей использования технологий х=(х

;…;х

обеспечивающий максимум выпуска продукции в стоимостном выражении:

(21)

При ограничениях на лимитируемые ресурсы

(22)

∑

xcЦФ

max

),1(0

),1(

njx

mibxa

jij

=≥

=≤

∑

xcЦФ

max

),1(

mibxa

jij

=≤

∑

И условии неотрицательности

),1(0 njx

=≥

(23)

3.2.3 Задача о смесях

В пищевой промышленности возникает проблема составления рабочих

смесей на основе исходных материалов, которые обеспечивали бы получение

конечного продукта, обладающего определенными свойствами. К этой группе

задач относятся задачи о выборе диеты, составления кормового рациона в

животноводстве, составления смесей сырья для получения средневзвешенных

показателей и т.п.

Высокий уровень затрат на сырье и необходимость повышения

эффективности производства выдвигает на первый план следующую задачу:

получить продукцию с заданными свойствами при наименьших затратах на сырье.

Например, имеется N видов сырья, с различными показателями качества -

всего m показателей качества. A

показатели качества для каждого вида сырья.

Базовая величина показателей b

. Обозначим через c

стоимость единицы (тонны)

сырья с различными показателями качества.

Требуется составить смесь таким образом, чтобы средневзвешенные

показатели качества не превышали базовых величин. X

– это количество сырья

каждого вида, обеспечивающее базовые показатели при минимальных затратах:

Математическая модель задачи:

Найти

(24)

При ограничениях

(25)

3.3 Симплексный метод

Для решения задач линейного программирования используют симплекс-

метод или метод последовательного улучшения плана. Суть метода

заключается в переборе крайних точек плана и нахождение в каждой точке

значения целевой функции. Все точки, в которых целевая функция принимает

наихудшие значения, не нужны. Остается точка, в которой ЦФ принимает

оптимальное значение (максимум или минимум).

Целевая функция – это функция, характеризующая оптимальное решение

(качественная характеристика процесса). В зависимости от технологического

процесса целевая функция может стремится, либо к максимуму, либо к

∑

xcЦФ

min

),1(0

),1(

njx

mibxa

jij

=≥

=≤

∑

минимуму. Например, прибыль должна быть максимальна, а затраты на перевозки

готовой продукции минимальны.

Для аналитического решения задач линейного программирования

разработан специальный алгоритм направленного перебора вершин. Этот

алгоритм обеспечивает переход от одной вершины к другой в таком направлении,

при котором значение целевой функции от вершины к вершине улучшается.

В геометрии есть понятие «симплекс». Симплексом тела в k-мерном пространстве

называют k+1 его вершин. Так, для плоскости при k=2 симплексом будут три

вершины треугольника. Аналитический метод решения задачи линейного

программирования называю симплекс-методом. Вычисления, обеспечивающие

определение значения целевой функции и переменных в одной вершине называют

итерацией.

Симплексный метод предполагает:

• Умение находить начальный опорный план.

• Наличие признака оптимальности опорного плана.

• Умение переходить нехудшему опорному плану.

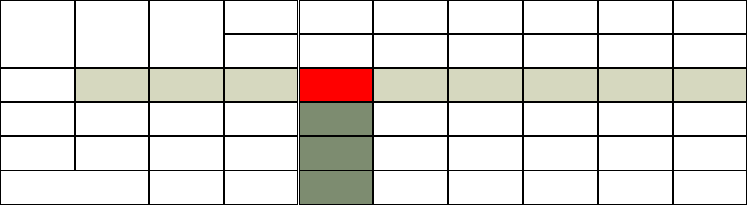
Начальный опорный план представлен в таблице 4. Рассмотрим составление

начального опорного плана на примере задачи о наилучшем использовании

ресурсов. Начальный опорный план составляется на основе математической

модели (19), (20).

Таблица 4 – Начальный опорный план

X1 X2 X3 X4 X5 X6 X7 БП СБ А

2 6 -1 3 0 0 0

X5 0 4 1 3 0 1 1 0 0

X6 0 3 2 1 0 0 0 1 0

X7 0 3 0 1 4 1 0 0 1

ЦФj-Cj 0 -2 -6 1 -3 0 0 0

При составлении начального опорного плана в столбец «БП» вносятся

базовые переменные. Базовыми называются переменные, которые входят в одно

уравнение модели с коэффициентом 1, а в остальные с коэффициентом 0.

Например, в задаче о наилучшем использовании ресурсов базовые переменные

указывают на возможные остатки ресурсов.

Столбец «СБ» содержит значения прибыли с единицы продукции

соответствующих базовых переменных. Столбец «А» содержит значения равные

запасам сырья на предприятии. Столбец «Х1» содержит в первой строке значение

прибыли с единицы выпускаемой продукции, далее расход каждого вида ресурса

на выпуск единицы продукции Х1. Аналогичным образом заполняются

оставшиеся столбцы X2, X3, X4, столбцы Х5, Х6, Х7 заполняются аналогично

таблице 4.

Последняя строка начального опорного плана – это стока целевой функции

или индексная строка. Значения в индексной строке рассчитываются по

следующим формулам:

(26)

Значения целевой функции равно соответственно Δ

Решения бывают допустимыми и оптимальными. Каждое решение имеет

свой признак.

Признак 1.

Определяет является ли полученное решение допустимым. Решение является

допустимым, если в столбце свободных членов (целевая функция не

рассматривается) все члены не отрицательные.

Признак 2.

Признак 2 определяет наличие оптимального решения, при этом возможны два

варианта:

1) целевая функция имеет минимальное значение в том случае, когда все

элементы в строке целевой функции (свободный член не рассматривается)

будут отрицательными.

2) Целевая функция имеет максимальное значение в том случае, когда все

элементы в строке целевой функции будут положительными.

При неоптимальности начального опорного плана необходимо перейти к

нехудшему опорному плану.

Для этого определяется разрешающий столбец. Разрешающий столбец

определяется по максимальной по модулю оценке в индексной строке, в таблице 4

разрешающий столбец – Х2.

Разрешающая строка соответствует минимальному симплексному

отношению, которое определяется как А/Х

. Х

– это соответствующие значения

разрешающего столбца. В таблице 4 разрешающая строка первая.

В новой симплекс-таблице необходимо из столбца «БП» вывести одну из

переменных и ввести другую. Для более короткого решения рекомендуется

выводить из базиса переменную, соответствующую переменной разрешающей

строки и внести переменную соответствующую базисному столбцу. В столбец

«СБ» вносится значение прибыли с единицы продукции введенной новой

базисной переменной.

Кроме того, при составлении новой симплекс-таблицы необходимо

выполнять следующие правила симплексных преобразований:

1) все элементы разрешающей строки делятся на разрешающий элемент;

2) все элементы разрешающего столбца равны нулю, за исключением

разрешающего элемента, он равен 1;

3) все остальные элементы таблицы находят по правилу прямоугольника.

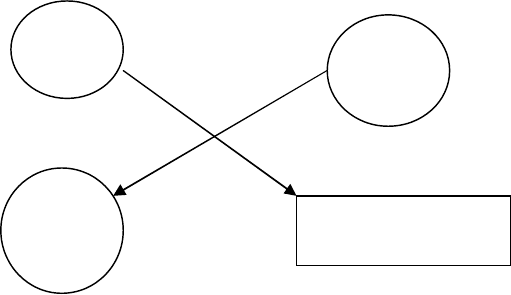
Правило прямоугольника формулируется следующим образом:

Чтобы получить элемент aij новой симплексной таблицы необходимо из

произведения угловых элементов главной диагонали вычесть произведение

угловых элементов побочной диагонали и полученное число разделить на

разрешающий элемент (на рисунке 3 выделенный рамкой)

jjj

CАСБ

АСБ

−⋅=∆

⋅=∆

∑

Рисунок 3 - Правило прямоугольников

Диагональ, содержащая разрешающий и искомый элемент новой таблицы,

называют главной, а другую побочной. Прямоугольник мысленно выстаивают

таким образом, чтобы в элементы главной диагонали входил искомый элемент и

разрешающий элемент, а в элементы побочной диагонали элемент разрешающего

столбца и элемент разрешающей строки.

После проведения симплексных преобразований определяется

оптимальность нового опорного плана. Если в индексной строке нет

отрицательных элементов, то план оптимален и прибыль от реализации

продукции максимальна. При этом вид выпускаемой продукции и остатки

ресурсов смотрятся в столбце «БП», а их количество в столбце «А». А если в

индексной строке есть отрицательные элементы, то строится новый опорный план

и определяется его оптимальность.

3.4 Построение двойственных задач и их свойства

Каждой задаче линейного программирования соответствует двойственная

задача. Двойственная задача формулируется по следующим правилам:

1) каждому i-му ограничению исходной задачи соответствует переменная

двойственной задачи, которую называют двойственной переменной;

2) каждой переменной исходной задачи соответствует ограничение

двойственной задачи (ДЗ). Например, в исходной задаче три переменных, значит,

ДЗ должна иметь три ограничения;

3) матрица коэффициентов при двойственных переменных в ограничениях

двойственной задачи является транспонированной матрицей коэффициентов при

переменных в ограничениях исходной задачи. Например,













357

211

. Тогда

транспонированная матрица













А .

4) если в исходной задаче ограничения имеют знаки неравенств ≤, то в ДЗ ≥.

5) правые части ограничений в ДЗ равны коэффициентам при переменных в

целевой функции исходной задачи;

Разреш_элемент

ij0

i0j

главная

побочная