Коротков А. Эконометрика. Вводный курс. Решение задач
Подождите немного. Документ загружается.


Задача 2
Как было показано на семинаре, у стационарного процесса AR (2)
Ey
t
= 0,
γ
0
= Dy
t
=
(1 − ϕ
2
) Dε
t
(1 + ϕ
2
) (1 − ϕ
1
− ϕ
2
) (1 + ϕ
1
− ϕ
2
)
,
γ
1
= cov (y
t
, y
t−1
) =
ϕ
1
Dε
t
(1 + ϕ
2
) (1 − ϕ
1
− ϕ
2
) (1 + ϕ
1
− ϕ
2
)
.
В данном случае Dε
t
= 1, поэтому γ
0
≈ 89.8079, γ
1
≈ 88.7636. Следовательно,
если Ey
1
= Ey
2
= 0, Dy
1
= Dy
2
= 89.8079, cov (y
1
, y
2
) = 88.7636, и эти случайные
величины независимыми с ошибками, то получается стационарный в слабом
смысле ряд, поскольку тогда Ey
t
= 0, Dy
t
= 89.8079 для всех t = 1, 2, . . ..
Задача 3
Процесс является с тационарным, если его среднее, дисперсия и все автокорре-
ляции постоянны во времени. Таким образом, необходимо найти все эти вели-
чины и убедиться, что они не зав исят от t. Заметим, что поскольку ε
t
, ε
t−1
—
независимые нормальные величины, то случайная в еличина y
t
= ε
t
−θε
t−1
также
нормальна со средним Ey
t
= E [ε
t
− θε
t−1
] = 0 и дисперсией Dy
t
= D [ε
t
− θε
t−1
] =
1 + θ
2
σ
2
. Поэтому
Ex
t
= 1 · P (y
t
> 0) + 0 · P (y
t
< 0) = P (y
t
> 0) = 0.5 (не зависит от t),
Dx
t
= E [x
t
]
2
− [Ex
t
]
2
= 1
2
· P (y
t
> 0) + 0 · P (y
t
< 0) − (0.5)
2
=
= 0.5 − 0.25 = 0.25 (не зависит от t),
ACF (k) =
E [x
t
x
t−k
] − E [x
t
] E [x
t−k
]
Dx
t
= 4E [x
t
x
t−k
] − 1.
Поскольку
x
t
x
t−k
=
1, если y
t
> 0 & y
t−k
> 0,
0, иначе,
то
ACF (k) = 4P (y
t
> 0 & y
t−k
> 0) − 1.
Так как при k > 2 имеем cov (y
t
, y
t−k
) = 0, то эти величины будут независимы-
ми. Значит, при k > 2
ACF (k) = 4P (y
t
> 0) · P (y
t−k
> 0) − 1 = 4 · 0.5 · 0.5 − 1 = 0.
40

При k = 1 искомая вероятность будет равна
P (y
t
> 0 & y
t−1
> 0) =
=
ZZZ
1 {x − θy > 0}1 {y − θz > 0}dF
ε
t
(x) dF
ε
t−1
(y) dF
ε
t−2
(z) =
=
Z
+∞
−∞
dF
ε
t−1
(y)
Z
+∞
θy
dF
ε
t
(x)
Z
y/θ
−∞
dF
ε
t−2
(z)
!
=
=
Z
+∞
−∞
1 − Φ
θy
σ
Φ
y
θσ
1
√
2πσ
e
−
y
2
2σ
2
dy =
=
Z
+∞
−∞
(1 − Φ (θey)) Φ
ey
θ
1
√
2π
e
−
1
2
ey
2
dey =
=
Z
+∞
−∞
(1 − Φ (θy)) Φ
y
θ
dΦ (y) ,
где 1 {·} — индикаторная функция. Видно, что эта вероятность не зависит от t,
следовательно, стационарность процесса {x
t
} доказана — его среднее, дисперсия
и все автокорреляционные функции постоянны во времени.
Задача 4
Чтобы найти производную ∂y
t
/∂ε
t−s
, достаточно найти представление процесса
в виде MA (∞). Из уравнения процесса следует, что
y
t
=
1 − 0.8L
1 − 1.1L + 0.3L
2
ε
t
.
Значит, всё, что осталось сделать, это разложить данную дробь в сумму про-
стых дробей, как это делается при интегрировании рациональных дробей. Кор-
нями многочлена 1 −1.1x + 0.3x
2
, x ∈ C, являются x
1
= 2 и x
2
= 5/3. Пользуясь
методом неопределённых коэффициентов, получаем разложение
1
1 − 1.1L + 0.3L
2
=
1
1 −
1
2
L
1 −
3
5
L
=
6
1 −
3
5
L
−
5
1 −
1
2
L
.
41
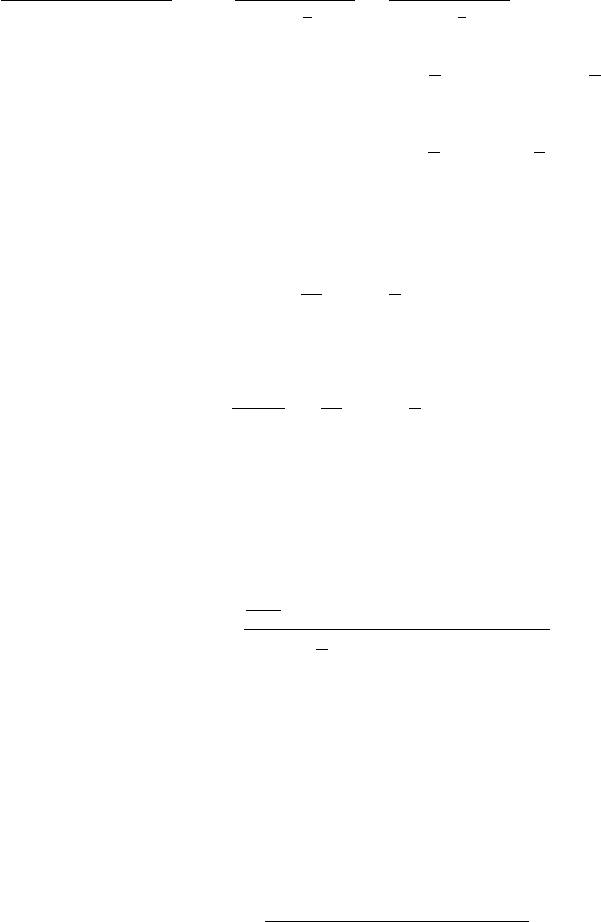
Тогда, применяя формулу суммы бес конечно убывающей геометрической про-
грессии, имеем:
1 − 0.8L
1 − 1.1L + 0.3L
2
=
6 (1 − 0.8L)
1 −
3
5
L
−
5 (1 − 0.8L)
1 −
1
2
L
=
= (1 − 0.8L)
"
6
∞
X
s=0
3
5
L
s
− 5
∞
X
s=0
1
2
L
s
#
=
= (1 − 0.8L)
∞
X
s=0
6
3
5
s
− 5
1
2
s
L
s
.
Проделав арифметические преобразования, окончательно получаем:
y
t
=
∞
X
s=0
3
2
s
− 2
3
5
s
ε
t−s
,
таким образом,
∂y
t
∂ε
t−s
=
3
2
s
− 2
3
5
s
.
Задача 5
• Основная формула для расчета эмпирического коэффициента автокорре-
ляции k-го порядка для ряда {y
t
}, t = 1, . . . , T , имеет вид
r
k
=
1
T −k
P
T
t=k+1
(y
t
− ¯y) (y
t−k
− ¯y)
1
T
P
T
t=1
(y
t
− ¯y)
2
,
где ¯y = (1/T )
P
T
t=1
y
t
. В нашем случае ¯y = 5, тогда r
1
= 9/16.
Примечание. На практике при подсчёте автоковариации чаще всего ис-
пользуют не T − k, а T в знаменателе. При больших размерах выборок
различие между формулами незначительно (коэффициент T/ (T − k) бли-
зок к единице), а, поскольку в теории временн´ых рядов асимптотика за-
нимает первое место, впредь можно пользоваться формулой
r
k
=
P
T
t=k+1
(y
t
− ¯y) (y
t−k
− ¯y)
P
T
t=1
(y
t
− ¯y)
2
.
42

• Предполагаем, что коэффициенты автокорреляции более высокого поряд-
ка равны нулю, тогда оказывается, что имеем дело с процессом MA (1).
Для этого процесса
ρ
1
= −
θ
1 + θ
2
,
поэтому для отыскания θ нужно решить систему
−θ/
1 + θ
2
= −2/5
|θ| < 1
(неравенство учитывает, что процесс обратимый). В итоге получаем θ =
1/2.
• Поскольку процесс, как легко видеть, стационарен, то автокорреляции
можно считать по формуле ρ
k
= 0.5ρ
k−1
+ 0.25ρ
k−2
. Имеем
ρ
3
=
1
2
·
7
12
+
1
4
·
2
3
=
11
24
,
ρ
4
=
1
2
·
11
24
+
1
4
·
7
12
=
3
8
.
•
σ
2
z
= Dz
t
= D (ε
t
+ 0.5ε
t−1
− 0.5ε
t−2
) =
= Dε
t
+ 0.25Dε
t−1
+ 0.25Dε
t−2
=
= 1.5σ
2
ε
= 6,
откуда σ
2
ε
= 4.
• Пусть y
t
= ϕ
1
y
t−1
+ ϕ
2
y
t−2
+ ϕ
3
y
t−3
+ ε
t
. Тогда
σ
2
ε
= E (y
t
− ϕ
1
y
t−1
− ϕ
2
y
t−2
− ϕ
3
y
t−3
)
2
= . . . =
=
1 + ϕ
2
1
+ ϕ
2
2
+ ϕ
2
3
γ
0
+2 (ϕ
1
ϕ
2
− ϕ
1
+ ϕ
2
ϕ
3
) γ
1
−2 (ϕ
2
− ϕ
1
ϕ
3
) γ
2
−2ϕ
3
γ
3
.
• Нет. Оба процесса нестационарны и σ
2
x
= σ
2
y
= +∞.
43
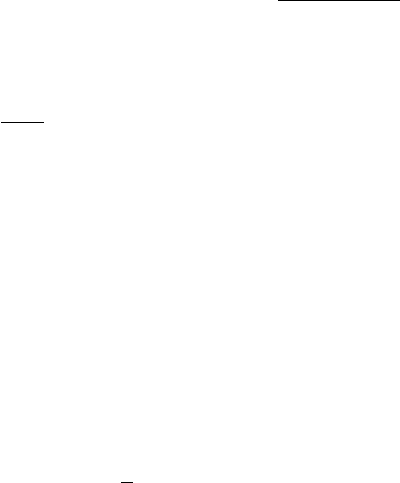
Задача 6
В прошлой домашней работе было показано, что автокорреляционная функция
любого стационарного процесса AR (2) может быть представлена в виде
ρ
k
= A
1
G
k
1
+ A
2
G
k
2
, (12)
где G
i
— числа, обратные корням характеристического уравнения, A
i
— некото-
рые константы. Если оба корня вещественны, ρ
k
будет затухающей экспонентой.
В случае комплексных корней можно показать, что ρ
k
имеет вид затухающей
синусоиды:
ρ
k
= d
k
sin (kα + β)
sin β
,
где константы вычисляются по следующему алгоритму. Пусть ϕ
1
и ϕ
2
— пара-
метры процесса, тогда:
1. d =
√
−ϕ
2
,
2. α = arccos [ϕ
1
/ (2d)] ,
3. β = arctg [((1 + d
2
) / (1 − d
2
)) tgα] .
В нашем случае получаем ρ
k
= (0.71)
k
sin (1.5k + 1.547).
Задача 7
Пользуясь формулой (14) и тем, что в данном симметричном случае A
1
= A
2
=
1/2, G
1
= 1/5 = −G
2
, получаем
ρ
k
=
1
2
G
k
1
+ (−G
1
)
k
=
G
k
1
, k — чётное,
0, иначе.
Задача 8
Из общих св ойст в ARMA-процессов следует, что {y
t
} является временным ря-
дом типа AR (2), поскольку частная автокорреляция PACF (k) равна нулю при
k > 3. Поэтому для процесса {y
t
} подходящей является модель AR (2).
Так как данные не позволяют идентифицировать среднее значение процесса
{y
t
}, будем считать, что Ey
t
= 0. Тогда
y
t
= ϕ
1
y
t−1
+ ϕ
2
y
t−2
+ ε
t
, (13)
44

где ε
t
— белый шум. Поскольку для любого AR (p)-процесса PACF (p) = ϕ
p
, то
ϕ
2
= 0.5. Кроме того, по определению, PACF (1) = ACF (1). Будем использо-
вать обозначения γ
k
= cov (y
t
, y
t−k
), ρ
k
= γ
k
/γ
0
= ACF (k). Умножая обе части
равенства (1) на y
t−1
, беря математические ожидания и принимая во внимание
независимость y
t−2
и ε
t
, получаем γ
1
= ϕ
1
γ
0
+ ϕ
2
γ
1
, откуда ρ
1
= ϕ
1
/ (1 − ϕ
2
).
Так как ρ
1
= 0.8, ϕ
2
= 0.5, то ϕ
1
= 0.4.
Проделывая те же действия с y
t−2
, получаем γ
2
= ϕ
1
γ
1
+ ϕ
2
γ
0
, откуда ρ
2
=
ϕ
1
ρ
1
+ ϕ
2
= 0.82. Аналогично, ρ
3
= ϕ
1
ρ
2
+ ϕ
2
ρ
1
= 0.728. Итак, y
t
= 0.4y
t−1
+
0.5y
t−2
+ ε
t
, ACF (1) = 0.8, ACF (2) = 0.82, ACF (3) = 0.728.
Задача 9
Приведённая регрессия позволяет провести ADF-тест с константой и трендом.
Величина соответствующей статистики есть DF = (0.9869 − 1) /0.0037 = −3.5405.
5%-ное критическое значение в данном случае есть −3.4145, поэтому на 5%-ном
уровне значимости гипотезу о наличии единичного корня можно отвергнуть.
Наиболее подходящая модель для этого ряда — trend stationery.
Задача 10
Запишем прогноз на s шагов вперёд
y
n+s
= δ + φy
n+s−1
+ ε
n+s
− θε
n+s−1
и проведём s − 1 рекуррентную подстановку в правой части:
y
n+s
= δ + φ (δ + φy
n+s−2
+ ε
n+s−1
− θε
n+s−2
) + ε
n+s
− θε
n+s−1
=
= . . . = δ
s−1
X
l=0
φ
l
+ φ
s
y
n
+ ε
n+s
+ (φ − θ)
s−2
X
l=0
φ
l
ε
n+s−l−1
− φ
s−1
θε
n
=
= δ
s−1
X
l=0
φ
l
+ φ
s
y
n
− φ
s−1
θε
n
+ e
n+s
,
где e
n+s
= ε
n+s
+(φ − θ)
P
s−2
l=0
φ
l
ε
n+s−l−1
. Дисперсия ошибки прогноза, учитывая
независимость импульсов, вычисляется просто:
De
n+s
= D
ε
n+s
+ (φ − θ)
s−2
X
l=0
φ
l
ε
n+s−l−1
!
= σ
2
1 + (φ − θ)
2
s−2
X
l=0
φ
2l
!
=
= σ
2
1 + (φ − θ)
2
s−2
X
l=0
φ
2l
!
= σ
2
1 + (φ − θ)
2
1 − φ
2(s−1)
1 − φ
2
!
.
45

Устремляя s к бесконечности в по следнем выражении и принимая во внимание,
что |φ| < 1, получаем
lim
s−→∞
De
n+s
= σ
2
1 + (φ − θ)
2
1
1 − φ
2
= σ
2
1 − 2φθ + θ
2
1 − φ
2
.
Задача 11
Пусть z
n
:= ∆y
n
. Тогда из уравнения процесса z
n
−µ = φ (z
n−1
− µ) + ε
n
можно
вывести выражение для значения процесса через k периодов:
z
n+k
= µ
1 − φ
k
+ φ
k
z
n
+
k−1
X
l=0
φ
l
ε
n+k−l
.
Поскольку y
n+s
= y
n
+
P
s
k=1
z
n+k
, найдём
s
X
k=1
z
n+k
=
s
X
k=1
"
µ
1 − φ
k
+ φ
k
z
n
+
k−1
X
l=0
φ
l
ε
n+k−l
#
=
= µs − µ
s
X
k=1
φ
k
+ z
n
s
X
k=1
φ
k
+
s
X
k=1
k−1
X
l=0
φ
l
ε
n+k−l
,
теперь получаем
y
n+s
= y
n
+ µs + φ
1 − φ
k
1 − φ
(z
n
− µ) + e
n+s
,
где e
n+s
= ε
n+s
+ (1 + φ) ε
n+s−1
+ . . . +
1 + φ + φ
2
. . . + φ
s−1
ε
n+1
.
Задача 12
1.
bµ =
1
n
X
y
i
= µ +
1
n
X
ε
i
p
−→ µ + Eε
i
= µ,
где сходимость обеспечивается ЗБЧ Хинчина. Асимптотическая нормаль-
ность обеспечивается ЦПТ Линдберга-Леви:
√
n (bµ − µ) =
1
√
n
X
ε
i
=
√
n
1
n
X
ε
i
− Eε
1
=⇒ N
0, σ
2
.
46

2. Перепишем оценку в привычном виде:
eµ =
X
w
i
y
i
= µ +
X
w
i
ε
i
.
Введём случайную величину
ξ
i
:=
2i
n + 2
ε
i
,
тогда bµ перепишется как
eµ = µ +
1
n
X
ξ
i
.
Воспользовавшись ЗБЧ Чебышёва (поскольку моменты величин ξ
i
разли-
чаются) и тем, что Eξ
i
= 0, заключаем, что
eµ = µ +
1
n
X
ξ
i
p
−→ µ + p lim
1
n
X
ξ
i
= µ.
Для исследования на асимптотическую нормальность запишем далее
√
n (eµ − µ) =
√
n
X
w
i
ε
i
=
1
√
n
X
ξ
i
=
√
n
1
n
X
ξ
i
−
1
n
X
µ
i
,
где µ
i
≡ Eξ
i
≡ 0. Воспользуемся ЦПТ Линдберга-Феллера:
√
n
1
n
X
ξ
i
−
1
n
X
µ
i
=⇒ N
0, ¯σ
2
,
где ¯σ
2
= lim
n−→∞
P
σ
2
i
/n, σ
2
i
= Dξ
i
. Вычислим эту асимптотическую диспер-
сию:
1
n
X
Dξ
i
=
1
n
X
4i
2
σ
2
(n + 2)
2
=
4σ
2
n (n + 2)
2
X
i
2
=
= . . . =
2σ
2
3
·
(n + 1) (2n + 1)
(n + 2)
2
−→
n−→∞
4σ
2
3
.
47
Приложения
Приложение 1. Задачи из экзаменов
Задача 1
Пусть истинная модель (data generating model) есть y
t
= βx
t
+ ε
t
. Является
ли МНК-оценка
b
β, полученная при оценивании коэффициента уравнения y
t
=
α + βx
t
+ υ
t
несмещённой оценкой истинного значения β?
Решение Да, является.
Мы знаем, что при оценивании регрессии y
t
= α + βx
t
+ υ
t
коэффициент
b
β
выражается по формуле
b
β =
P
(x
t
− x) (y
t
− y)
P
(x
t
− x)
2
.
Подставим в эту формулу выражение истинной зависимости y от x: y
t
= βx
t
+ε
t
:
b
β =
P
(x
t
− x) (βx
t
+ ε
t
− (βx + ε))
P
(x
t
− x)
2
=
P
β (x
t
− x)
2
+
P
(x
t
− x) ε
t
P
(x
t
− x)
2
=
=
P
β (x
t
− x)
2
+
P
(x
t
− x) ε
t
P
(x
t
− x)
2
= β +
P
(x
t
− x) ε
t
P
(x
t
− x)
2
.
Тогда
E
b
β = β +
P
(x
t
− x) Eε
t
P
(x
t
− x)
2
= β.
Таким образом, оценка
b
β не смещена.
Задача 2
Имеется стандартная линейная модель: y = Xβ + ε, Dε = σ
2
I
n
. Пусть Λ — невы-
рожденная диагональная n×n матрица. Рассмотрим оценку
e
β = (X
0
ΛX)
−1
(X
0
Λy).
а) Является ли эта оценка несмещённой?
б) Что вы можете сказать о т очност и этой оценки, по сравнению с оценкой
метода наименьших квадратов?
49
