Коротков А. Эконометрика. Вводный курс. Решение задач
Подождите немного. Документ загружается.

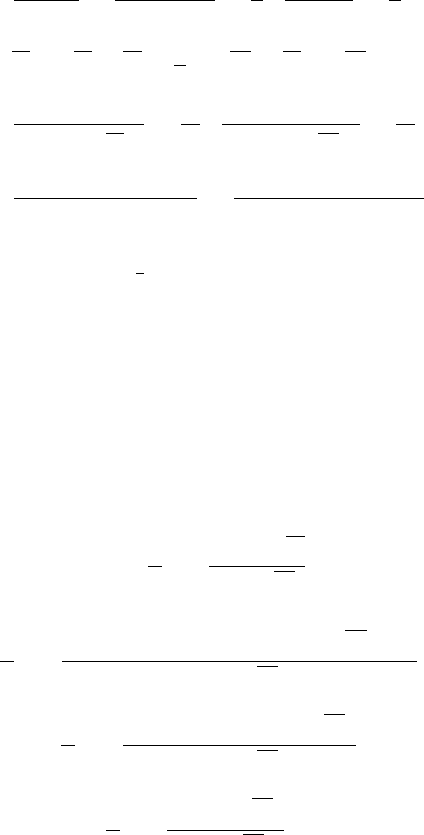
Регрессионный анализ
Задача 1
Обозначим новые МНК-оценки коэффициентов как ˜α и
˜
β. Посмотрим, как из-
менятся оценки, их дисперсии, а также величина R
2
. Используя известные фор-
мулы, получаем:
˜
β =
P
z
i
y
i
P
z
2
i
=
P
(cx
i
) y
i
P
(cx
i
)
2
=
1
c
·
P
x
i
y
i
P
x
2
i
=
1
c
ˆ
β,
˜α = Y −
˜
βZ = Y −
1
c
ˆ
β · cX = Y −
ˆ
βX = ˆα,
D
˜
β =
σ
2
P
Z
i
− Z
2
=
1
c
2
·
σ
2
P
X
i
− X
2
=
1
c
2
D
ˆ
β,
D˜α =
σ
2
P
Z
2
i
n
P
Z
2
i
− (
P
Z
i
)
2
=
σ
2
P
X
2
i
n
P
X
2
i
− (
P
X
i
)
2
= Dˆα.
Поскольку
e
Y
i
= ˜α +
˜
βZ
i
= ˆα +
1
c
ˆ
β · cX
i
=
b
Y
i
, то R
2
не изменится. Итак, дис-
персия оценки углового коэффициента уменьшится, если c > 1 (и увеличится в
противном случае). Это видно и из формулы для дисперсии: она тем меньше,
чем больше разброс значений регрессора вокруг своего среднего значения (см.
замечание на с.45 в шестом издании Магнуса et al).
Задача 2
а) Вычислим матожидание оценки
˜
β:
E
˜
β =
1
n
n
X
i=1
EY
i
− EY
X
i
− X
=
=
1
n
n
X
i=1
E (α + βX
i
+ ε
i
) − E
α + βX + ¯ε
X
i
− X
=
=
1
n
n
X
i=1
(α + βX
i
) −
α + βX
X
i
− X
=
=
1
n
n
X
i=1
β
X
i
− X
X
i
− X
= β.
20
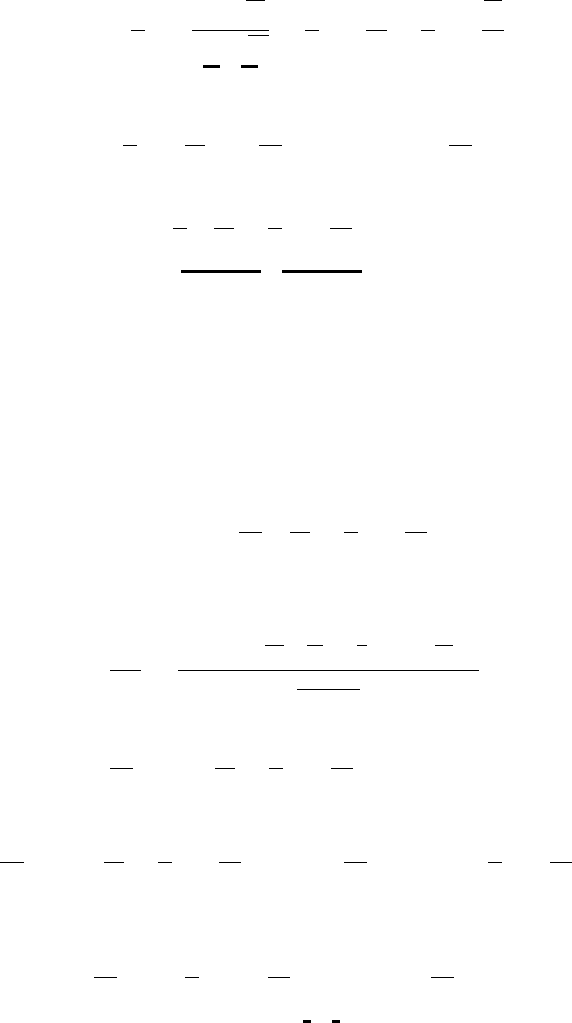
Оценка несмещённая. Представим её в следующем виде:
˜
β =
1
n
n
X
i=1
Y
i
− Y
X
i
− X
| {z }
x
i
=
1
n
n
X
i=1
Y
i
x
i
−
1
n
n
X
s=1
Y
x
s
=
=
1
n
n
X
i=1
1
x
i
Y
i
−
1
n
2
n
X
i=1
Y
i
!
n
X
s=1
1
x
s
!
=
=
n
X
i=1
1
n
1
x
i
−
1
n
n
X
s=1
1
x
s
!
| {z }
c
i
Y
i
=
n
X
i=1
c
i
Y
i
.
Оценка линейная.
б) Для в ычисления дисперсии воспользуемся тем, что Y
i
— некоррелирован-
ные случайные величины с дисперсиями σ
2
.
D
˜
β = D
n
X
i=1
c
i
Y
i
!
=
n
X
i=1
c
2
i
DY
i
= σ
2
n
X
i=1
c
2
i
=
= σ
2
n
X
i=1
1
n
2
1
x
i
−
1
n
n
X
s=1
1
x
s
!
2
.
в) Воспользуемся неравенством Коши-Буняковского:
D
˜
β
D
ˆ
β
=
σ
2
P
n
i=1
1
n
2
1
x
i
−
1
n
P
n
s=1
1
x
s
2
σ
2
P
n
i=1
x
2
i
=
=
1
n
2
n
X
i=1
1
x
i
−
1
n
n
X
s=1
1
x
s
!
2
·
"
n
X
i=1
x
2
i
#
>
>
1
n
2
"
n
X
i=1
1
x
i
−
1
n
n
X
s=1
1
x
s
!
x
i
#
2
=
1
n
2
"
n
X
i=1
1 −
1
n
n
X
s=1
x
i
x
s
!#
2
=
=
1
n
2
n −
1
n
n
X
s=1
1
x
s
n
X
i=1
x
i
|{z}
=0
2
=
1
n
2
· n
2
= 1.
21
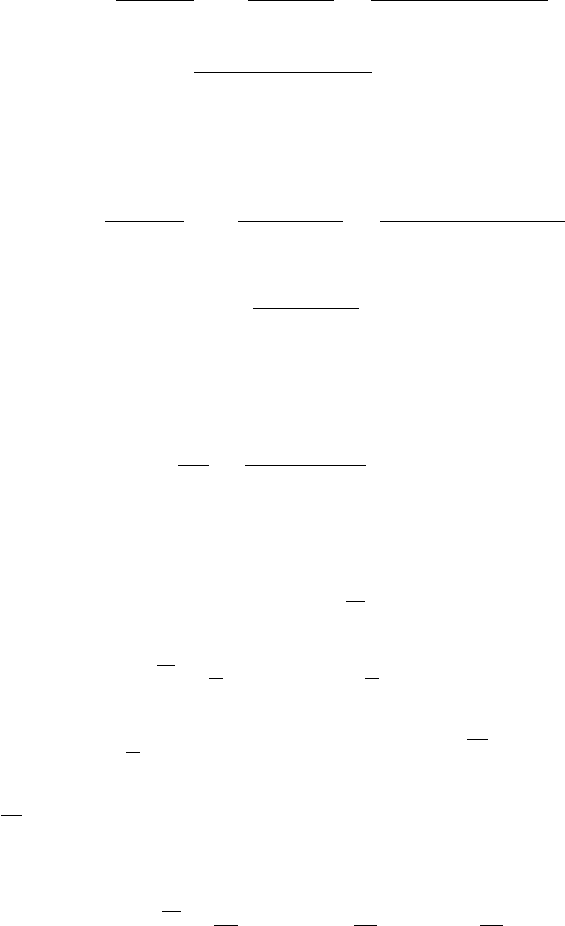
Задача 3
а)
E
˜
β = E
P
Z
i
Y
i
P
Z
i
X
i
=
P
Z
i
EY
i
P
Z
i
X
i
=
P
Z
i
E (βX
i
+ u
i
)
P
Z
i
X
i
=
=
P
Z
i
(βX
i
+ Eu
i
)
P
Z
i
X
i
= β.
Оценка несмещённая.
б) Найдём дисперсию оценки. Игреки некоррелированы, поэ тому
D
˜
β = D
P
Z
i
Y
i
P
Z
i
X
i
=
P
Z
2
i
DY
i
(
P
Z
i
X
i
)
2
=
P
Z
2
i
D (βX
i
+ u
i
)
(
P
Z
i
X
i
)
2
=
=
P
Z
2
i
σ
2
(
P
Z
i
X
i
)
2
.
Дисперсия оценки МНК равна σ
2
/
P
n
i=1
X
2
i
. Сра вним их. По неравенству Коши-
Буняковского сразу же получаем
D
˜
β
D
ˆ
β
=
P
Z
2
i
P
X
2
i
(
P
Z
i
X
i
)
2
> 1.
Задача 4
а) Нетрудно найти оценку ˜α путём минимизации суммы квадратов отклонений
P
(Y
i
− a)
2
по параметру a и по лучить ˜α = Y . Далее,
E˜α = EY =
1
n
E
X
Y
i
=
1
n
E
X
Y
i
=
=
1
n
E
X
(α + βX
i
+ ε
i
)
= α + βX.
Таким образом, оценка яв ляется несмещённой тогда и только тогда, когда либо
β = 0, либо X = 0.
б) Игреки некоррелированы, поэтому
D˜α = DY =
1
n
2
X
DY
i
=
1
n
2
X
σ
2
=
σ
2
n
,
22

что меньше, чем у оценки МНК (если
P
X
i
6= 0):
Dˆα =
σ
2
P
X
2
i
n
P
X
2
i
− (
P
X
i
)
2
.
в) Имеются две оценки. Вторая оценка смещённая, зато её дисперсия мень-
ше, чем у первой оценки, которая несмещённая. Какую из оценок выбрать?
Одним из компромиссов в таком случае может быть сравнение оценок на осно-
ве среднеквадратической ошибки
9
(mean-square error, MSE). По определению,
MSE о ценки
ˆ
θ параметра θ есть
MSE
ˆ
θ
≡ E
ˆ
θ − θ
2
= D
ˆ
θ +
bias
ˆ
θ
2
,
где bias
ˆ
θ
= E
ˆ
θ − θ. Очевидно, для несмещённых оценок MSE
ˆ
θ
= D
ˆ
θ.
Итак, MSE (ˆα) = Dˆα, а MSE (˜α) = D˜α + (bias (˜α))
2
= D˜α + β
X
2
. Отсюда
видно, что малых значениях параметра β предпочтительной оказывается вто-
рая оценка, а при достаточно больших β и n лучше пользо ва ть ся МНК-оценкой.
Задача 5
Используя линейность оценок МНК по игрекам, получаем:
ˆ
β =
n
P
X
i
(Y
1i
+ Y
2i
) − (
P
X
i
) (
P
(Y
1i
+ Y
2i
))
n
P
X
2
i
− (
P
X
i
)
2
=
n
P
X
i
Y
1i
− (
P
X
i
) (
P
Y
1i
)
n
P
X
2
i
− (
P
X
i
)
2
+
n
P
X
i
Y
2i
− (
P
X
i
) (
P
Y
2i
)
n
P
X
2
i
− (
P
X
i
)
2
=
=
b
β
1
+
b
β
2
.
bα =
1
n
X
(Y
1i
+ Y
2i
) −
1
n
X
X
i
b
β
1
+
b
β
2
=
=
1
n
X
Y
1i
−
1
n
X
X
i
b
β
1
+
1
n
X
Y
2i
−
1
n
X
X
i
b
β
2
=
= bα
1
+ bα
2
.
9
иногда говорят, среднеквадратического отклонения.
23
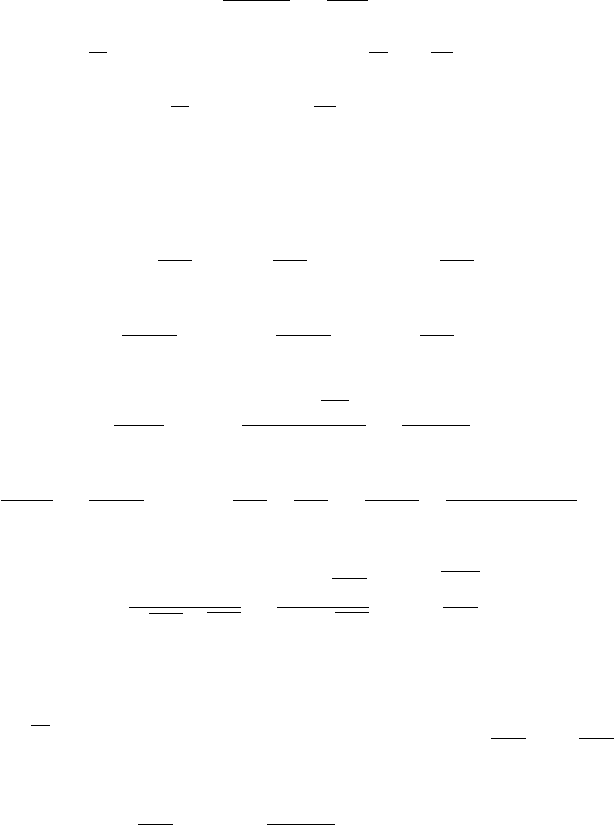
Задача 6
а)
b
β =
P
x
i
y
i
P
x
2
i
=
S
xy
S
xx
,
e
i
= Y
i
− Y = Y
i
− bα −
b
βX
i
= Y
i
−
Y −
b
βX
−
b
βX
i
=
=
Y
i
− Y
−
b
β
X
i
− X
= y
i
−
b
βx
i
.
Отсюда
X
e
2
i
=
X
y
2
i
+
b
β
2
X
x
2
i
− 2
b
β
X
x
i
y
i
=
= S
yy
+
S
2
xy
S
2
xx
S
xx
− 2
S
xy
S
xx
S
xy
= S
yy
−
S
2
xy
S
xx
,
s
2
=
1
n − 2
X
e
2
i
=
1
n − 2
S
yy
−
S
2
xy
S
xx
.
R
2
= 1 −
ESS
T SS
= 1 −
S
yy
−
S
2
xy
S
xx
S
yy
=
S
2
xy
S
xx
S
yy
= r
2
xy
.
s
2
b
β
=
s
2
P
x
2
i
=
1
n − 2
S
yy
−
S
2
xy
S
xx
1
S
xx
=
1
n − 2
S
xx
S
yy
− S
2
xy
S
2
xx
.
б)
r
xy
=
S
xy
√
S
xx
p
S
yy
=
S
xy
√
S
xx
S
xx
p
S
yy
=
b
β
s
S
xx
S
yy
.
в)
X
b
Y
i
− Y
2
= RSS = TSS −ESS = S
yy
−
S
yy
−
S
2
xy
S
xx
=
S
2
xy
S
xx
.
ESS = S
yy
−
S
2
xy
S
xx
=
1 −
S
2
xy
S
xx
S
yy
S
yy
=
1 − r
2
xy
S
yy
.
24
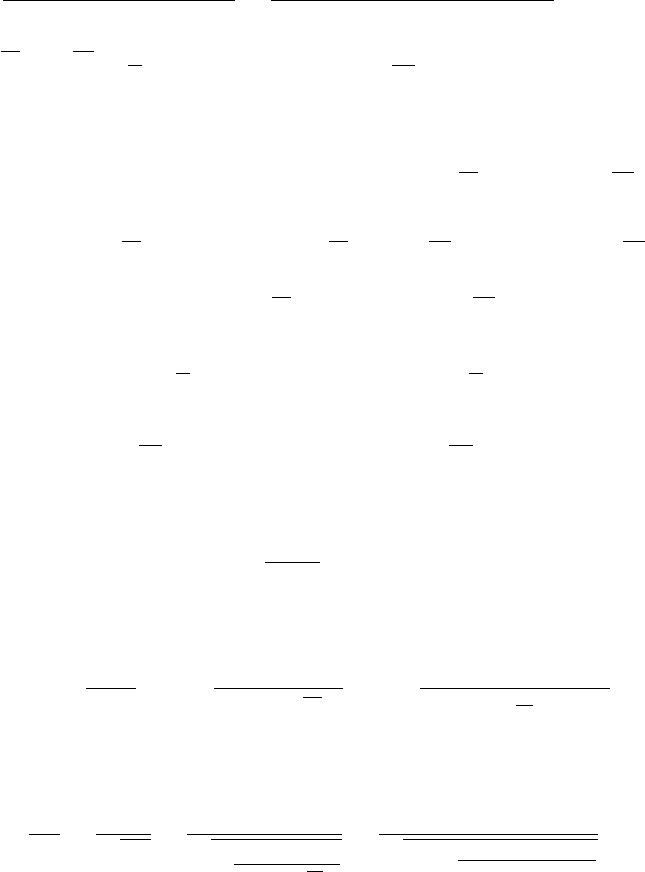
Задача 7
а) для модели парной регрессии, МНК-оценки коэффициентов выражаются сле-
дующими формулами:
b
β
2
=
n
P
X
i
Y
i
−
P
X
i
P
Y
i
n
P
X
2
i
− (
P
X
i
)
2
=
50 · 12.120 − 24.909 · 17.704
50 · 16.269 − 24.909
2
= 0.855,
b
β
1
= Y −
b
β
2
X =
1
n
X
Y
i
−
b
β
2
X
X
i
=
1
50
(17.704 − 0.855 · 24.909) = −0.072.
Сумма квадратов остатков:
X
e
2
i
=
X
Y
i
−
b
β
1
−
b
β
2
X
i
2
=
X
Y
i
− Y
−
b
β
2
X
i
− X
2
=
=
X
Y
i
− Y
2
− 2
b
β
2
X
Y
i
− Y
X
i
− X
+
b
β
2
2
X
X
i
− X
2
=
=
X
Y
i
− Y
2
−
b
β
2
2
X
X
i
− X
2
=
=
X
Y
2
i
−
1
n
X
Y
i
2
−
b
β
2
2
X
X
2
i
−
1
n
X
X
i
2
=
= 67.886 −
1
50
17.704
2
− 0.855
2
16.269 −
1
50
24.909
2
= 58.796.
Оценка дисперсии ошибок:
s
2
=
1
n − 2
X
e
2
i
= 1.225.
Коэффициент детерминации:
R
2
= 1 −
ESS
T SS
= 1 −
P
e
2
i
P
Y
i
− Y
2
= 1 −
58.796
67.886 −
1
50
17.704
2
= 0.046.
б) гипотеза H
0
: β
1
= 0 проверяется при помощи стандартного t-теста:
t
1
=
b
β
1
s
b
β
1
=
b
β
1
q
s
2
b
β
1
=
b
β
1
r
s
2
P
X
2
i
n
P
(
X
i
−X
)
2
=
−0.072
q
1.225
16.269
50·16.269−24.909
2
= −0.224.
25
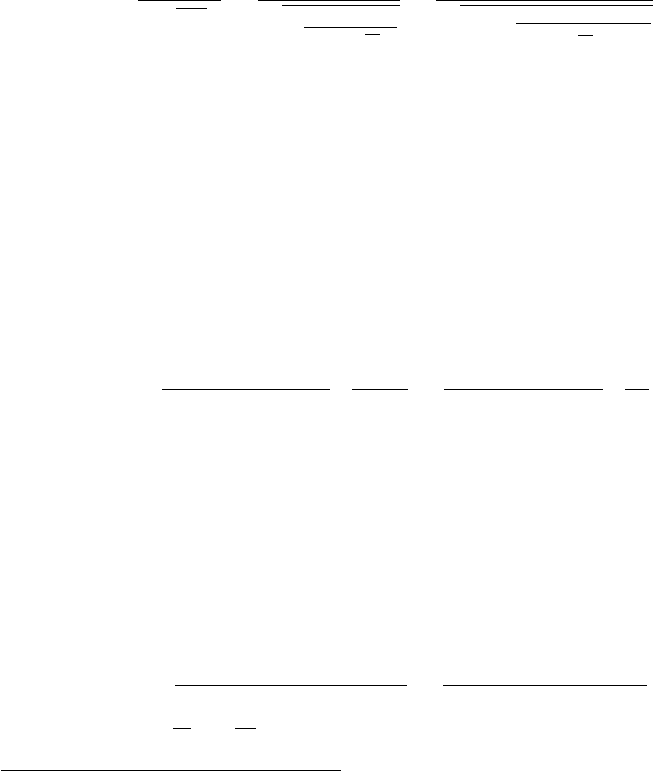
Соответствующее P -значение можно найти из таблиц для t (48)-распределения
или с помощью какого-нибудь программного обеспечения, например, Excel:
p-value = P (|t (48)| > |t
1
|) = 2F
t(48)
(−|t
1
|) = 0.824 > 0.05,
поэтому гипотезу H
0
не отвергаем.
в) аналогично проверяется гипотеза H
0
: β
2
= 1.7:
t
2
=
b
β
2
− 1.7
p
s
b
β
2
=
b
β
2
− 1.7
r
s
2
1
P
(
X
i
−X
)
2
=
0.855 − 1.7
q
1.225
1
16.269−
1
50
24.909
2
= −1.500,
p-value = 2F
t(48)
(−|t
2
|) = 0.140 > 0.05,
поэтому гипотезу H
0
не отвергаем.
г) Данную гипотезу тестируем при помощи F -теста.
10
Регрессия с ограни-
чением — это регрессия вида Y = 1.7X + ε. Сумма квадратов остатков в ней
равна:
ESS
R
=
X
(Y
i
− 1.7X
i
)
2
=
X
Y
2
i
− 3.4
X
X
i
Y
i
+ 1.7
2
X
X
2
i
=
= 67.886 − 3.4 · 12.12 + 2.89 · 16.269 = 73.695,
F =
ESS
R
− ESS
UR
ESS
UR
·
n − k
q
=
73.695 − 58.796
58.796
·
48
2
= 6.082,
p-value = 1 − F
F (2,48)
(6.082) = 0.00442 < 0.05,
⇒ гипотезу H
0
отвергаем.
Задача 8
а) Урав нение регрессии Y
i
на X
i
при наличии свободного члена имеет вид Y
i
=
α + βX
i
+ ε
i
. Оценки коэффициентов:
b
β =
n
P
X
i
Y
i
−
P
X
i
P
Y
i
n
P
X
2
i
− (
P
X
i
)
2
=
10 · 8360 − 207 · 462
10 · 5023 − 207
2
≈ −1.63,
bα = Y −
b
βX ≈ 46.2 − (−1.63) · 20.7 = 79.95.
10
См. Магнус et al, 6-е издание, с. 84.
26

Далее считаем
b
Y
i
= 79.95 − 1.63X
i
для каждого i. Считаем R
2
:
R
2
=
RSS
T SS
=
P
b
Y
i
− Y
2
P
Y
i
− Y
2
=
1962.0
2279.6
= 0.8607.
б) Уравнение регрессии Y
i
на X
i
при отсутствии свободного члена имеет вид
Y
i
= βX
i
+ ε
i
. Тогда
b
β =
P
X
i
Y
i
P
X
2
i
=
8360
5023
≈ 1.66.
В случае отсутствия константы равенство
T SS = ESS + RSS,
вообще говоря, не выполняется, и корректно коэффициент детерминации не
определяется. Можно попробовать вычислить его двумя способами:
R
2
(1)
=
RSS
T SS
=
3424.7
2279.6
= 1.50,
R
2
(2)
= 1 −
ESS
T SS
= 1 −
9710.1
2279.6
= −3.26.
В случае отсутствия константы не обязательно R
2
∈ [0, 1].
в) & г) эти случаи совпадают как друг с другом, так и со случаем а).
Задача 9
а) МНК-оценка для α равна Y и находится стандартно. Несмещённой оценкой
дисперсии ошибок для k-мерной множественной регрессии является величина
P
e
2
i
/ (n − k). Значит, в нашем случае bσ
2
= s
2
=
P
e
2
i
/ (n − 1).
б)
Dbα = D
Y
=
1
n
2
· n · DY
i
=
σ
2
n
.
в) Точное (а не только асимптотическое, как в общем случае) нормаль-
ное распределение оценка будет иметь, если ошибки распределены нормаль-
но, т.е. ε
i
∼ N (0, σ
2
). Оценка, как легко видеть, в этом случае также будет
иметь нормальное распределение (как сумма независимых нормальных вели-
чин): bα ∼ N (0, σ
2
/n). Тогда следствием из основного следствия из леммы Фи-
шера (см. соответствующий раздел матстатистики) будет то, что
√
n
Y − α
q
1
n−1
P
Y
i
− Y
2
∼ T
n−1
.
27
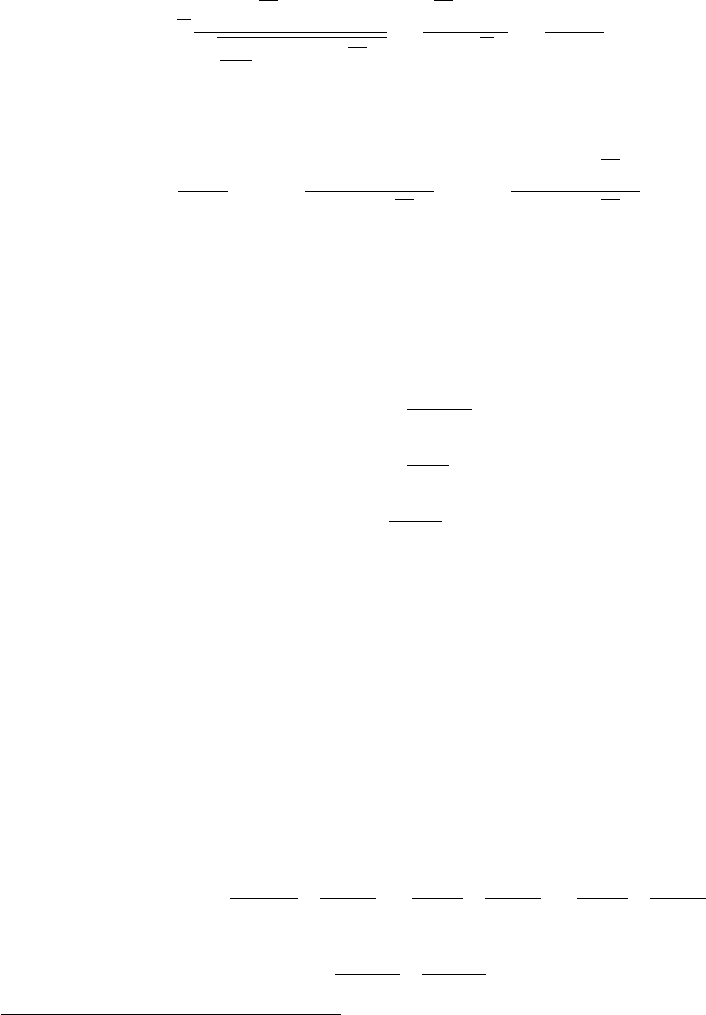
Преобразуем это выражение с учётом того, что Dbα = s
2
bα
= s
2
/n:
√
n
Y − α
q
1
n−1
P
Y
i
− Y
2
=
Y − α
s/
√
n
=
bα − α
s
bα
∼ T
n−1
.
г)
R
2
= 1 −
ESS
T SS
= 1 −
P
(Y
i
− bα)
2
P
Y
i
− Y
2
= 1 −
P
Y
i
− Y
2
P
Y
i
− Y
2
= 1 − 1 = 0.
Задача 10
а) Считаем t-статистики для каждого из коэффициентов (кроме константы
— её (не-) значимость принципиальной роли не играет):
t
1
= −
0.0098
0.0034
= −2.8824,
t
2
= −
5.62
3.42
= −1.6433,
t
3
=
0.044
0.009
= 4.8889.
Зададимся 5%-ным уровнем значимости. То гда значение 95%-ной двусто-
ронней ква нтили (2.5%-ной точки) есть (учитывая, что число степеней
свободы равно 24 − 4 = 20) 2.0860. Сравнивая это значение с абсолютны-
ми значениями t-статистик, заключаем, что первый и третий регрессоры
значимы, а вт орой нет. Если тестировать гипотезы на 10 %-ном уровне зна-
чимости, то значение квантили будет 1.7247, что ничего принципиально
не меняет. Соответствующие p-значения для трёх статистик рав ны, соот-
ветственно, 0.0092, 0.1159 и 8.8299E-05.
б) Считаем F-статистику по известной формуле:
11
F =
R
2
1 − R
2
·
n − k
k − 1
=
RSS
ESS
·
n − k
k − 1
=
RSS
ESS
·
n − k
k − 1
=
=
110.32
21.43
·
24 − 4
4 − 1
= 34.3195.
11
См. Магнус et al, 6-е издание, стр. 79
28

5%-ная точка (95%-ная односторонняя квантиль) распределения Фишера
с (3, 20) степенями свободы равна 3.0984. Нулевая гипотеза о незначимости
очень уверенно отвергается (p-значение равно 1.9643E-07).
в) Единственная гипотеза, которую можно проверить при имеющихся дан-
ных, состоит в том, что поквартальной сезонности нет. Пусть α, β, γ —
коэффициенты перед фиктивными переменными, отвечающими, соответ-
ственно, за первый, второй и третий кварталы. Таким образом, можно
тестировать нулевую гипотезу о том, что α = β = γ = 0, т.е. что сезон-
ных эффектов не наблюдается. Для этого воспользуется F -тестом. В дан-
ном случае регрессией с ограничением является исходная регрессия, где
α = β = γ = 0. Значит, ESS
R
= 21.43. Далее, из исходной модели получа-
ем T SS = RSS
R
+ESS
R
= 110.32+21.43 = 131.75. Из подобного равенства
для модели без ограничения (при этом T SS, конечно, не зависит от мо-
дели!) получаем, что ESS
UR
= T SS − RSS
UR
= 131.75 − 118.20 = 13.55.
Считаем F -статистику.
12
Заметим, что q = 3, а k = 4 + 3 = 7.
F =
(ESS
R
− ESS
UR
) /q
ESS
UR
/(n − k)
=
(21.43 − 13.55) /3
13.55 /(24 − 7)
= 3.2955.
При верной нулевой гипотезе эта статистика распределена как F (3, 20).
Критическим уровнем является 3.1968, что меньше. Следовательно, нуле-
вая гипотеза (на 5%-ном уровне значимости) не очень уверенно, но отвер-
гается. Соответствующее p-значение составляет 0.0458.
Задача 11
а) Регрессия может считаться качественной только в том случае, если она не
содержит незначимых коэффициентов. В этом смысле регрессия (4) пло-
ха, т.к. коэффициенты при регрессорах EDU и EXP ER являются незна-
чимыми на 5 %-ном уровне. У остальных регрессий таких проблем нет
(незначимость константы в регрессии (2) не должна вводить в заблужде-
ние).
Сравнивать по прогностической силе вторую регрессию со всеми осталь-
ными нельзя, т.к. различаются зависимые переменные. Тот факт, что ре-
грессия (4) имеет больший R
2
по сравнению с (1) и (3), частично является
12
См. Магнус et al, 6-е издание, стр. 83
29
