Коротков А. Эконометрика. Вводный курс. Решение задач
Подождите немного. Документ загружается.


результатом увеличения числа регрессоров, поэтому для решения о срав-
нении регрессии (4) с (1) и (3) следует применять некую другую характе-
ристику, например, R
2
adj
= 1 − (1 − R
2
)
n−1
n−k
. Получаем, что для регрессии
(1) R
2
adj
= 0.37, для (3) R
2
adj
= 0.57, для (4) R
2
adj
= 0.6. Таким образом, и
по этому критерию регрессия (4) более информативна, чем (1) и (3). При
сравнении (1) и (3) регрессий, обладающей наибольшей прогностической
силой следует признать (3).
б) В регрессии (1) коэффициент при AGE означает, на сколько в среднем
вырастет зарплата при увеличении возраста на год при прочих равных. В
регрессии (2) коэффициент при ln AGE показывает, на сколько процентов
в среднем увеличивает зарплату увеличение на 1% возраста при прочих
равных.
Задача 12
Сначала вычислим t-статистику для коэффициента при W . Она равна t =
1.98/0.7949 ≈ 2.491. Эта статистика при нулевой гипотезе распределена соглас-
но распределению Стьюдента с n − 2 степенями свободы. Следовательно, для
проверки значимости коэффициента осталось найти n и с оот ве тст вующую про-
центную точку распределения T
n−2
. F -статистика для проверки значимости
регрессии в целом равна
F =
R
2
1 − R
2
·
n − k
k − 1
=
R
2
1 − R
2
(n − 2) .
Кроме того, т.к. регрессия парная, то F = t
2
, где t есть t-статистика для коэф-
фициента при W . Поэтому
n = 2 + t
2
1 − R
2
R
2
= 2 + 2.491
2
·
1 − 0.756
0.756
≈ 4,
с учётом того, что n целое, и ошибок округлений. 2.5%-ная точка распределения
T
n−2
равна t
0.025
(2) = 4.303. Следовательно, гипотеза о незначимости стипендии
для среднего балла не отвергается. Возможно, не хватило данных, ведь всего 4
наблюдения (в Новосибирске не так уж много университетов :-).
Задача 13
Первый вопрос — задача с параметром, параметр — число наблюдений. Ответ:
нет, если не знает числа наблюдений; да, если знает. Покажем это. Пусть число
30
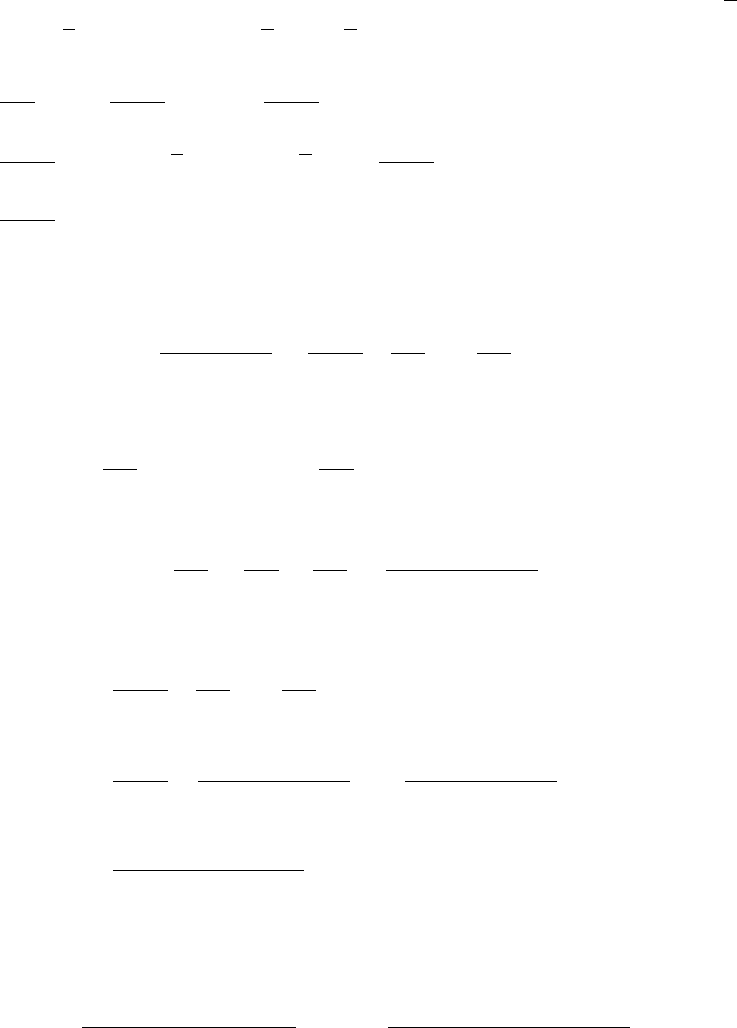
наблюдений равно n. Используем уже знакомые обозначения: S
xx
=
P
(x
t
− x)
2
,
S
yy
=
P
(y
t
− y)
2
, S
xy
=
P
(x
t
− x) (y
t
− y). Тогда по стандартным формулам
b
β =
S
xy
S
xx
, s
2
=
1
n − 2
X
e
2
t
=
1
n − 2
X
y
t
− bα −
b
βx
t
2
= (3)
=
1
n − 2
X
(y
t
− y) −
b
β (x
t
− x)
2
=
1
n − 2
X
S
yy
− 2
b
βS
xy
+
b
β
2
S
xx
=
=
1
n − 2
S
yy
−
b
βS
xy
.
Соответственно,
s
2
b
β
=
S
yy
−
b
βS
xy
(n − 2) S
xx
=
1
n − 2
S
yy
S
xx
−
S
xy
S
xx
2
!
. (4)
Отсюда
S
yy
S
xx
= (n − 2) s
2
b
β
+
S
yy
S
xx
2
= (n − 2) s
2
b
β
+
b
β
2
.
Аналогично,
bγ =
S
xy
S
yy
=
S
xy
S
xx
S
yy
S
xx
=
b
β
(n − 2) s
2
b
β
+
b
β
2
, (5)
s
2
bγ
=
1
n − 2
S
xx
S
yy
−
S
xy
S
yy
2
!
= (6)
=
1
n − 2
1
(n − 2) s
2
b
β
+
b
β
2
−
b
β
(n − 2) s
2
b
β
+
b
β
2
2
=
=
s
2
b
β
(n − 2) s
2
b
β
+
b
β
2
2
.
Таким образом, зная n, второй студент может вычислить оценки bγ и s
2
bγ
:
bγ =
0.5
(n − 2) · 0.025 + 0.25
, s
2
bγ
=
0.025
((n − 2) · 0.025 + 0.25)
2
.
31

Для ответа на второй вопрос задачи, нужно выяснить, как соотносятся меж-
ду собой t-статистики для проверки гипотез о незначимости коэффициентов β
и γ. А они попросту равны. Действительно, из формул (1) и (2) получаем:
t
β
=
b
β
s
b
β
=
S
xy
/S
xx
1
√
n−2
r
S
yy
S
xx
−
S
xy
S
xx
2
=
S
xy
√
n − 2
q
S
yy
S
xx
− (S
xy
)
2
,
а из формул (3) и (11) получаем:
t
γ
=
bγ
s
bγ
=
S
xy
/S
yy
1
√
n−2
r
S
xx
S
yy
−
S
xy
S
yy
2
=
S
xy
√
n − 2
q
S
yy
S
xx
− (S
xy
)
2
.
Таким образом, ответ на второй вопрос задачи отрицательный.
Задача 14
Рассмотрим равенство
C
t
= b
1
+ b
2
Y
t
+ b
3
C
t−1
+ bu
t
,
где b
i
(i = 1, 2, 3) — МНК-оценки параметров β
i
(i = 1, 2, 3). Поскольку это
равенство есть регрессия, то, по определению последней, bu
t
ортогонально Y
t
и
C
t−1
. Используя первое и третье равенства, получаем:
const + 0.92Y
t
+ e
t1
= b
1
+ b
2
Y
t
+ b
3
C
t−1
+ bu
t
=
= b
1
+ b
2
Y
t
+ b
3
(const + 0.78Y
t
+ e
t3
) + bu
t
=
= const + (b
2
+ 0.78b
3
) Y
t
+ b
3
e
t3
+ bu
t
.
Поскольку в выражениях слева и справа ошибки ортогональны регрессорам, то
оба эти выражения есть правые части некоторых регрессионных моделей. По-
скольку они равны, то и оценки оценённых с помощью них параметров также
с необходимостью будут равны. Значит, 0.92 = b
2
+ 0.78b
3
. Используя второе и
четвёртое равенства, можно получить аналогичные соотношения, из которых
будет следовать, что 0.55b
2
+ b
3
= 0.84. Решив полученную систему двух линей-
ных уравнений, получим ответ:
b
2
= 0.464, b
3
= 0.585.
32

Задача 15
а) Модель (2) можно записать так:
Y
1
.
.
.
Y
p
=
X
1
.
.
.
X
p
β +
u
1
.
.
.
u
p
, где
u
1
.
.
.
u
p
∼ N
0, σ
2
n
−1
1
··· 0
.
.
.
.
.
.
.
.
.
0 ··· n
−1
p
.
Таким образом, модель (2) есть линейная гетероскедастичная модель с ковари-
ационной матрицей
Ω = σ
2
n
−1
1
··· 0
.
.
.
.
.
.
.
.
.
0 ··· n
−1
p
.
Тогда (теорема Айткена) GLS (ОМНК) оценка в екто ра β будет эффективной
оценкой в классе линейных по Y
g
несмещённых оценок.
б) Поскольку оценка
e
β, полученная исследователем, является линейной так-
же и по исходным наблюдениям Y , то по теореме Гаусса-Маркова получаем
D
b
β 6 D
e
β.
Задача 16
В условии нигде не указано, каким методом были получены оценки. Будем
считать, что они были получены с помощью OLS (МНК).
а) Если общую оценку параметра β искать в виде выпуклой комбинации
(взвешенной суммы) двух имеющихся оценок, то в о бщем виде она запишется
как
e
β
θ
= θ
b
β
I
+ (1 − θ)
b
β
II
,
где 0 6 θ 6 1. Поскольку выборки независимы, дисперсия этой оценки легко
33
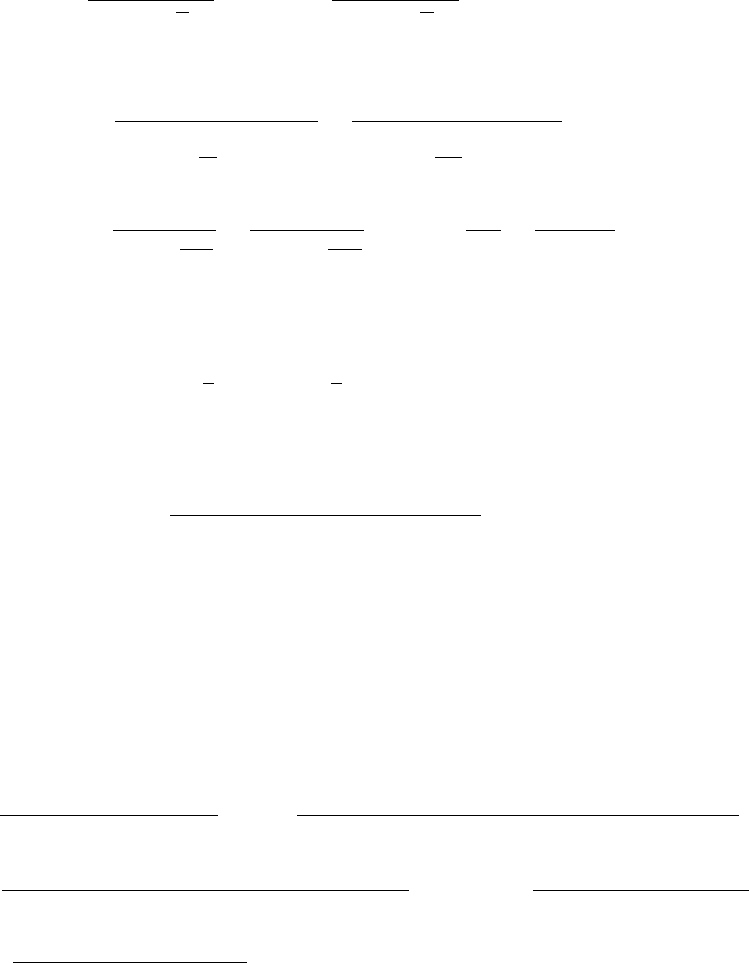
выражается через дисперсии оценок исследователей:
D
e
β
θ
= θ
2
D
b
β
I
+ (1 − θ)
2
D
b
β
II
=
= θ
2
σ
2
P
I
(x
t
− x
t
)
2
+ (1 − θ)
2
σ
2
P
II
(x
t
− x
t
)
2
=
= σ
2
θ
2
P
I
x
2
t
−
1
n
I
P
I
x
t
2
+
(1 − θ)
2
P
II
x
2
t
−
1
n
II
P
II
x
t
2
=
= σ
2
θ
2
600 −
100
2
20
+
(1 − θ)
2
2400 −
200
2
20
!
= σ
2
θ
2
100
+
(1 − θ)
2
400
!
.
Минимизируя последнее выражение по θ ∈ [0, 1], получим θ
∗
= 1/5 — оптималь-
ный выбор параметра взвешивания, а оптимальная
e
β
∗
θ
=
1
5
b
β
I
+
1 −
1
5
b
β
II
= 2.4.
б) По теореме Гаусса-Маркова оптимальной линейной несмещённой оценкой
β является
b
β =
n
P
I,II
x
t
y
t
−
P
I,II
x
t
P
I,II
y
t
n
P
I,II
x
2
t
−
P
I,II
x
t
2
. (7)
Суммы
P
I
x
t
y
t
и
P
II
x
t
y
t
можно найти из условий типа (3) для первой и вт орой
выборок. Таким образ ом, в выра жении для
b
β всё известно, и в итоге можно
получить
b
β = 1.6.
Задача 17
а)
E
e
β = E
P
λ
t
(x
t
− ¯x) (y
t
− ¯y)
P
λ
t
(x
t
− ¯x)
2
= E
P
λ
t
(x
t
− ¯x) (α + βx
t
+ ε
t
− (α + β¯x + ¯ε))
P
λ
t
(x
t
− ¯x)
2
=
= E
"
β
P
λ
t
(x
t
− ¯x)
2
+
P
λ
t
(x
t
− ¯x) (ε
t
−¯ε)
P
λ
t
(x
t
− ¯x)
2
#
= E
β +
P
λ
t
(x
t
− ¯x) (ε
t
−¯ε)
P
λ
t
(x
t
− ¯x)
2
=
= β +
P
λ
t
(x
t
− ¯x) E (ε
t
−¯ε)
P
λ
t
(x
t
− ¯x)
2
= β.
34
Таким образом, оценка
e
β действительно не смещена.
б) Более того, поскольку
e
β также линейна по y, то к ней применима теорема
Гаусса-Маркова, которая говорит о том, что в условиях стандартной линейной
модели регрессии, МНК-оценки являются на илучшими (в смысле наименьшей
дисперсии) среди всех линейных и несмещённых оценок. Таким образом, можно
сразу утверждать, что точность оценки
e
β не выше, чем у
b
β: D
e
β > D
b
β.
Задача 18
а) Обозначим зависимую переменную за Y
t
, а регрессо ры, соответственно, за
U
t
, NE
t
, S
t
, MW
t
, W
t
, G
t
(в порядке перечисления: б езраб от ица и фиктивные
переменные, индикаторы местоположения штата на северо-востоке, юге, сред-
нем западе и западе, и появления Гора в штате), t — номер штата. При этом,
конечно, NE
t
+ S
t
+ MW
t
+ W
t
≡ 1.
М1: Y
t
= α
1
U
t
+ α
2
NE
t
+ α
3
S
t
+ α
4
MW
t
+ α
5
W
t
+ ε
t
,
М2: Y
t
= α
1
U
t
+ α
2
NE
t
+ α
3
S
t
+ α
4
MW
t
+ α
5
W
t
+ α
6
G
t
+ ε
t
,
М3: Y
t
= α
0
+ α
1
U
t
+ α
2
NE
t
· G
t
+ α
3
S
t
· G
t
+ α
4
MW
t
· G
t
+ α
5
W
t
· G
t
+ ε
t
.
Заметьте, что в модели 1 и 2 константу включать нельзя (почему?).
б) 1) В рамках модели 2 тестируем гипотезу α
6
= 0. Если региональный
эффект отсутствует, то в рамках модели 3 тестируем гипотезу α
2
= α
3
= α
4
=
α
5
= 0. Однако если нет априорной информации об отсутствии регионального
эффекта, то отв ержение последней гипотезы может означать не значимость
появления Гора, а наличие регионального эффекта.
2) В рамках модели 1 или 2 тестируем гипотезу α
2
= α
3
= α
4
= α
5
.
3) В рамках модели 1 или 2 тестируем гипотезу α
2
= α
4
.
4) В рамках модели 1 или 2 тестируем гипотезу α
2
= α
4
& α
3
= α
5
.
5) Эта гипотеза не может быть тестирована ни в одной из моделей M1-M3.
Для тестирования оценки эффекта появления Гора по регионам необходима,
например, следующая модель:
Y
t
= α
0
+ α
1
U
t
+ α
2
NE
t
· G
t
+ α
3
S
t
· G
t
+ α
4
MW
t
· G
t
+ α
5
W
t
· G
t
+
+β
2
NE
t
+ β
3
S
t
+ β
4
MW
t
+ β
5
W
t
+ ε
t
,
в рамках которой на до тестировать гипотезу α
2
= α
3
= α
4
= α
5
. В рамках этой
модели можно было бы также тестировать и гипотезу 1): α
2
= α
3
= α
4
= α
5
= 0.
35
Задача 19
Распределение Лапласа характеризуется следующей плотностью и функцией
распределения:
f (x) =
1
2
e
−|x|
, F (x) =
x
Z
−∞
f (ξ) dξ =
1
2
e
x
, x < 0
1 −
1
2
e
−x
, x > 0
.
а) Обозначим за l (·) логарифмическую функцию прав доподобия, за 1 {·} —
индикаторную функцию. Тогда
l =
X
y
t
ln
1
2
e
x
0
t
β
· 1 {−x
0
t
β > 0} +
X
y
t
ln
1 −
1
2
e
−x
0
t
β
· 1 {−x
0
t
β 6 0}+
+
X
(1 − y
t
) ln
1
2
e
−x
0
t
β
·1 {−x
0
t
β 6 0}+
X
(1 − y
t
) ln
1 −
1
2
e
x
0
t
β
·1 {−x
0
t
β > 0}.
б) Напомним, что оценивание моделей дискретного выбора происходит в пред-
положении гомоскедастичности ошибок, но при этом оценить дисперсию оши-
бок не удаётся. Точнее говоря, можно оценить лишь отно шение вектора β к
корню из дисперсии ошибок. Probit-модель оценивалась из предположения о
единичной дисперсии. Распределение Лапласа имеет дисперсию, равную двум,
таким образом, коэффициент пропорциональности примерно равен
√
2.
Задача 20
Модель Probit с ошибкой N (0, σ
2
) описывается равенством
P (y
t
= 1) = Φ
x
0
t
β
σ
,
откуда видно, что для любого набора наблюдений (y
t
, x
t
), t = 1, . . . , n, модели
с параметрами (β, σ) и, например, (2β, 2σ) неразличимы. Иными словами, па-
раметры β и σ не идентифицируются раздельно. Поэтому, чтобы можно было
оценить параметры β, надо зафиксировать дисперсию σ
2
. Для модели Probit
естественно взять σ
2
= 1.
36

Задача 21
Наблюдение y
t
= c даёт в функцию правдоподобия « вклад» в виде вероятности
P (y
∗
t
< c) = P
ε
t
σ
<
c − x
0
t
β
σ
= Φ
c − x
0
t
β
σ
,
а наблюдение y
t
> c — в виде плотности
1
√
2πσ
exp
−
1
2σ
2
(y
t
− x
0
t
β)
2
.
Таким образом, функция правдоподобия есть
L =
Y
t: y
t
=c
Φ
c − x
0
t
β
σ
Y
t: y
t
>c
1
√
2πσ
exp
−
1
2σ
2
(y
t
− x
0
t
β)
2
.
Поскольку параметры β и σ входят в функцию правдоподобия раздельно, их
можно идентифицировать и оценить.
37
Анализ временных рядов
Задача 1
Во-первых, процесс {y
t
}, скорее всего, стационарный, поскольку коэффициенты
ϕ
1
= 1.7 и ϕ
2
= −0.72 удо влетв оряют системе неравенств
|ϕ
2
| < 1,
ϕ
2
+ ϕ
1
< 1,
ϕ
2
− ϕ
1
< 1,
которые являются необходимыми условиями стационарности процесса AR (2).
Воспользовавшись уравнениями Юла-Уокера, можно получить рекуррентное
соотношение для значений автокорреляционной функции ACF (k) ≡ ρ
k
этого
процесса:
ρ
k
= ϕ
1
ρ
k−1
+ ϕ
2
ρ
k−2
, k > 0. (8)
Для тех, кто изучал теорию конечно-разностных уравнений, уравнения (1) вме-
сте с начальными значениями ρ
1
и ρ
2
процесса уже достаточно, чтоб ы в об-
щем виде выписать его решение. Мы же, как и обычно, будем решать по-
сермяжному. В принципе, к какому-то разумному результату можно придти
и путём рекуррентных подстановок — желающие могут проделать это самосто-
ятельно.
Заметим, что уравнение (1) может быть переписано с использованием лаго-
вых операторов как
1 − ϕ
1
L − ϕ
2
L
2
ρ
k
= 0. (9)
Рассмотрим двучлен 1 − ϕ
1
x − ϕ
2
x
2
, x ∈ C. Он может быть разложен на мно-
жители над полем комплексных чисел. К счастью, в нашем случае корни ве-
щественные: x
1
= 5/4, x
2
= 10/9. Введя G
1
≡ 1/x
1
, G
2
≡ 1/x
2
, уравнение (2)
можно переписать в виде
(1 − G
1
L) (1 − G
2
L) ρ
k
= 0.
Для того, чтобы решить это уравнение, сведём его к уже решённому, а именно
к процессу AR (1). Обозначим ω
k
≡ (1 − G
2
L) ρ
k
. Тогда, очевидно, {ω
k
} — ACF
для авторегрессии первого порядка, значит
ω
k
= G
k−1
1
ω
1
. (10)
38
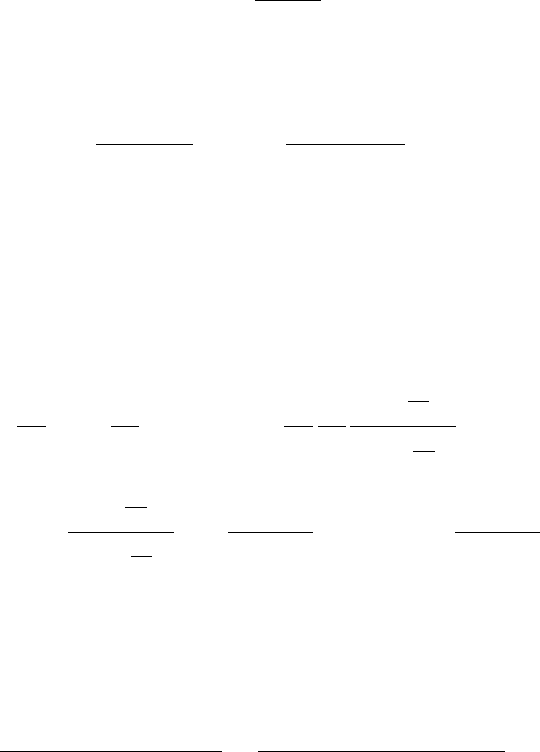
По определению ω
k
имеем
ω
1
= ρ
1
− G
2
ρ
0
=
ϕ
1
1 − ϕ
2
− G
2
.
По теореме Виета (вспоминаем школьную математику, другая здесь не понадо-
бится), G
1
+ G
2
= ϕ
1
, G
1
G
2
= −ϕ
2
, поэтому
ω
1
=
G
1
+ G
2
1 + G
1
G
2
− G
2
=
G
1
(1 − G
2
2
)
1 + G
1
G
2
.
Теперь начинаем рекуррентные подстановки. По определению ω
k
и с учётом (3)
имеем:
ρ
k
= G
2
ρ
k−1
+ ω
k
= G
2
G
2
ρ
k−2
+ ω
k−1
+ ω
k
= . . . =
= G
k
2
+
k
X
s=1
ω
s
G
k−s
2
= G
k
2
+
k
X
s=1
G
s−1
1
ω
1
G
k−s
2
=
= G
k
2
+ ω
1
G
k
2
G
1
k
X
s=1
G
1
G
2
s
= G
k
2
+ ω
1
G
k
2
G
1
G
1
G
2
1 −
G
1
G
2
k
1 −
G
1
G
2
=
= G
k
2
+ ω
1
G
k−1
2
1 −
G
1
G
2
k
1 −
G
1
G
2
=
ω
1
G
1
− G
2
G
k
1
+
1 −
ω
1
G
1
− G
2
G
k
2
.
Обозначив A
1
≡ ω
1
/ (G
1
− G
2
) , A
2
≡ 1 − A
1
, получим
ρ
k
= A
1
G
k
1
+ A
2
G
k
2
. (11)
Коэффициенты A
1
и A
2
равны, соответственно,
A
1
=
G
1
(1 − G
2
2
)
(G
1
− G
2
) (1 + G
1
G
2
)
=
0.8 (1 − 0.9
2
)
(0.8 − 0.9) (1 + 0.8 · 0.9)
≈
≈ −0.883721,
A
1
= 1 − A
1
≈ 1.883721.
Поскольку |G
i
| < 1 и |G
1
| 6= |G
2
|, т о урав нение (11) определяет ρ
k
как раз как
затухающую экспоненту:
ρ
k
= −0.88 · 0.8
k
+ 1.88 · 0.9
k
,
причём значение второго слагаемого довольно быстро убывает, так что |ρ
k
| ∼
0.8
k
при достаточно больш´их k.
39
