Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Numerical Modeling of the Electromechanical Interaction in MEMS

The ﬁrst monolithic approach one can think of is the basic Newton-Raphson al-

gorithm . At each step k the monolithic problem is linearized around the estimate

k−1

and a correction ∆U

is computed. Starting from the force imbalance for esti-

mate U

k−1

∆F

= F

ext

k−1

,V) −F

int

k−1

) , (30)

an update for the unknowns is computed using the linearized equilibrium equations

∆U

= K

−1

∆F

, (31)

and ﬁnally the solution is updated:

= U

k−1

+ ∆U

. (32)

The global tangent stiffness being updated every step, the Newton-Raphson up-

date is optimal in the sense that quadratic convergence is guaranteed in the vicinity

of the solution. For the Gauss-Seidel iterations (i.e. the staggered solution technique)

described by (25, 26) the variation of the coupling effects is not accounted for: only

the external forces and the pure mechanical and electrostatic operators are updated.

For that reason the convergence of staggered schemes is relatively slow. As men-

tioned, the faster convergence of the Newton-Raphson method comes at the price

of updating the stiffness. Therefore, an alternative procedure can be used where the

stiffness matrix is approximated or updated only for some iteration steps. These

methods are known as the modiﬁed Newton and quasi-Newton-Raphson method

[10]. For some type of problems these methods are overall computationally more

efﬁcient even though the convergence is slower.

3 Finding the pull-in curve

So far only the method for solving the displacement at a single applied voltage V

has been discussed. But for a proper characterization of the pull-in point a set of

successive solutions has to be found deﬁning the pull-in curve. Therefore it seems

very logical to use so-called incremental-iterative procedures. In this section we will

shortly discuss the different approaches that can be used to ﬁnd the pull-in curve.

3.1 Voltage stepping

The simplest incremental-iterative method is the voltage iterative method: the so-

lution is computed at a certain load V

by an iterative procedure (staggered or

monolithic, see previous section). The load is incremented by a value ∆V: V

i+1

+ ∆V). At this new voltage the solution is computed and next V is incremented

again, until a part of the pull-in curve has been determined. The problem with simple

325

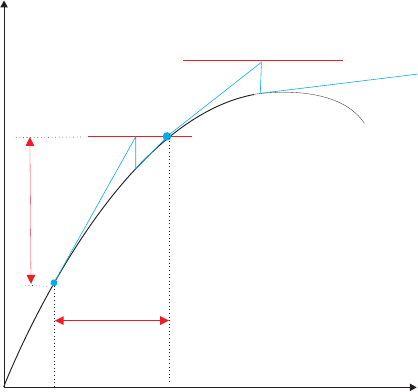
S.D.A. Hannot and D.J. Rixen

k + 1

∆U

∆V

i −1

Fig. 10 Several voltage iterations

voltage stepping is illustrated in ﬁgure 10: for a voltage above the pull-in limit no

solution can be found and thus the iterative solution techniques will not converge.

The voltage stepping method is conceptually similar to the load stepping method,

classically applied in non-linear buckling analysis of structures [4]. And also for

buckling analysis, the Newton-Raphson scheme is not well suited to handle limit

point buckling [28]. Limit point buckling was deﬁned by a maximum point of the

applied force in the force-displacement relationship, at which the mechanical tan-

gent stiffness matrix has a zero determinant [6, 41]. This phenomenon is very sim-

ilar to pull-in where the voltage-displacement relationship has a maximum and the

fully coupled tangent stiffness matrix has a zero determinant [37]. Therefore the

block Gauss-Seidel and Newton-Raphson algorithms will fail near the pull-in point

as well. Moreover they cannot ﬁnd the solutions in the unstable part of the pull-in

curve.

3.2 Path following methods

To overcome the shortcomings of the strategy described above where stepping is

performed on the voltage and the Newton-Raphson or Gauss-Seidel iterations used

to ﬁnd the corresponding response, one can combine the stepping and the solution

iterations in a uniﬁed iterative solution procedure where one constrains the norm

of the increment in the hyperspace that includes the driving parameter (the volt-

age in this case) and the response. These techniques were developed for buckling

326

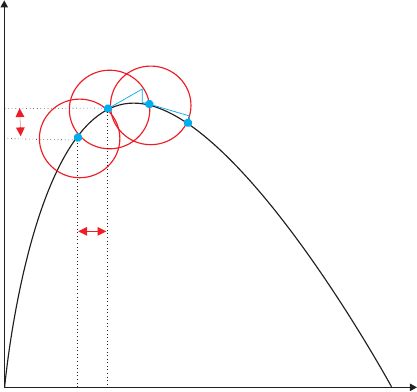
Numerical Modeling of the Electromechanical Interaction in MEMS

k + 1

∆

i −1

i + 1

Fig. 11 Several path following iterations

problems and are known as path-following methods [28]. Since buckling is a purely

mechanical problem, these algorithms were developed as being inherently mono-

lithic. However the concept of path-following can also be used to develop staggered

strategies [20].

Path-following methods go back to the early papers by E. Riks [35] and M.A. Cr-

isﬁeld [9]. The basic idea consists in adding to the set of equilibrium equations a

constraint on norm of the increment for U and V. The circular version of such a

constraint is shown in ﬁgure 11. The algorithm with a circular constraint is known

as the Riks-Crisﬁeld algorithm (or the arc-length method).

To apply such a circular constraint to ﬁnd the next point i+ 1 on the pull-in curve

(see ﬁgure 11) a separation is made between the total change (∆

, ∆

), and the

update of the increments during the iterative process (dV

k+1

,dU

k+1

) such that the

new estimate for the increments is written as

∆

k+1

= ∆

+ dU

k+1

, (33)

∆

k+1

= ∆

+ dV

k+1

. (34)

The iterations for the increment (∆

V,∆

U) stop when the point satisﬁes all equilib-

rium equations. During an update of the increments the norm of allowed total dis-

placement increment (structural dofs and potential dofs) augmented with the driving

parameter increment is kept constant:

∆

k+1

∆

k+1

+ ∆

k+1

= S

, (35)

327

S.D.A. Hannot and D.J. Rixen

where S is the constraint on the norm of the increment. The equation can also be

written as

∆

k+1

∆

k+1

+ ∆

k+1

= ∆

∆

+ ∆

. (36)

Substituting (33,34) in this last relation, one ﬁnds a constraint for the updates

(dU

k+1

,dU

k+1

). These constraints together with the linearized equilibrium equa-

tions around the latest estimate deﬁne the equations for the next estimate. For more

details on different methods using the path-following concept see e.g. [10].

In a block iterative procedure it proves to be very difﬁcult to use the full circular

constraint on all dofs because the full tangent stiffness is not known. But it is possi-

ble to assume that the problem is purely mechanical with an intricate external force

function of the potential V and displacements u:

ext

= f

ext

(u,v(V )) . (37)

In that case it is possible to write a constraint equation on the mechanical displace-

ments (u) and applied external load (V):

∆

k+1

∆

k+1

+ ∆

k+1

= ∆

∆

+ ∆

. (38)

Results obtained with an algorithm that used a linearized version of constraint (38)

were presented in [20].

3.3 Displacement stepping

Another way to construct the pull-in curve is to take as driving parameter a dis-

placement of the structure: a displacement dof is prescribed and an iterative solver

is used to compute the applied voltage needed to satisfy equilibrium. This approach

is schematically illustrated in ﬁgure 12.

However for problems with more than one dof this approach is not trivial since

the structural displacements (except the one chosen as driving parameter) and the

electric potentials need to be found. Therefore a relaxation scheme called DIPIE has

been proposed in the literature [5]. At a given iteration of the algorithm, an estimate

is known for the structural displacement. The algorithm uses the quadratic de-

pendency of f

ext

on the applied potential V in the 1D problem and assumes that this

is still a good assumption in a more complex geometry:

ext

(V ) =



ext

,V = 1)



, (39)

At equilibrium one must have for the structure

ext

= f

int

, (40)

where:

int

= K

u . (41)

328

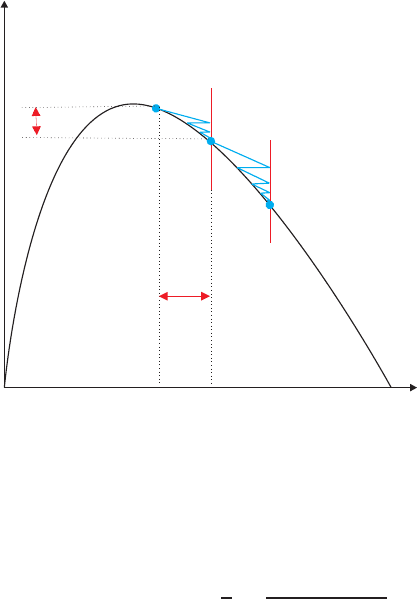
Numerical Modeling of the Electromechanical Interaction in MEMS

k + 1

∆U

∆V

i −1

i + 1

Fig. 12 Several displacement iterations

So an estimate of the voltage needed to satisfy equilibrium in the structure can be

constructed from an averaged force ratio

∑

e=1

int

)

ext

,V = 1)

, (42)

where e indicates those n dofs that experience the electric forces. Once this guess is

made an update of the mechanical force can be made:

int

k+1

) = V

ext

,V = 1) , (43)

which can be used to update the displacement. This can be repeated until conver-

gence.

3.4 Charge stepping

Another approach to travel along the pull-in curve is inspired by some strategies

used to control the motion of MEMS in practice [33, 38]: prescribe the total electric

charge instead of the voltage on the moving conductor. This idea is explained in

[20]. The voltage can be determined in a post processing step. The advantage of this

method is illustrated on the 1D example problem presented in sect. 1.2 and shown

in ﬁg. 4.

329

S.D.A. Hannot and D.J. Rixen

Coulomb’s law for the force on a point charge is:

QE , (44)

with E the ﬁeld outside the conductor.

Writing Gauss’ law for a control volume crossed by a unit conductor surface one

ﬁnds

sur f ace

EdA =

Q , (45)

which means that in 1D

E =

Q . (46)

Thus the force becomes equal to:

. (47)

Direct substitution of equation (46) into the force function, equation (12), gives

the same result. Therefore it is possible to consider the charge on the conductor

as the applied electric load and as driving parameter. Thus using (47) to write the

mechanical equilibrium equation one ﬁnds

k(x −x

) +

= 0 , (48)

which can be written as

Q =

k(x

−x) . (49)

The charge at a zero gap (x = 0) is:

Q(x = 0) =

. (50)

Thus the normalized charge becomes:

Q(x = 0)

−x

, (51)

which is a monotonously increasing function as can be seen in ﬁg. 13. Hence unlike

the voltage-displacement curve it does not have an extremum and moreover it shows

less non-linear behavior. It will be easier to follow the charge-displacement curve

and extract from it the voltage-displacement curve and pull-in characteristics.

For more complicated structures it is not possible to simply apply the charge

on the moving structure, because the charge distribution over the boundary of the

structure depends on the shape of the electric domain. However due to the assump-

tion that electrodes are perfect conductors it is known that the potential over the

conductor is constant, which effectively deﬁnes an equipotential constraint. Thus

the charge can be applied on one dof of the conductor boundary only in combina-

330

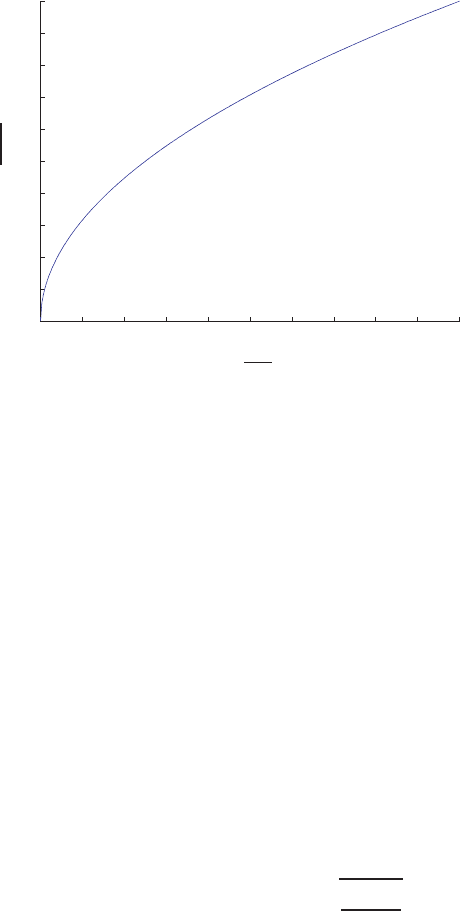
Numerical Modeling of the Electromechanical Interaction in MEMS

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Q(x=0)

−x

Fig. 13 1D charge-displacement curve

tion with the equipotential constraint. This equipotential constraint can be imple-

mented using several methods, for instance with Lagrange multipliers. The equi-

librium equations when the charge is imposed can again be solved using staggered

or monolithic approaches (see previous section). So far only a block Gauss-Seidel

approach for charge loading can be found in the literature [20].

3.5 General remarks

An overview of all the different methods to compute the pull-in curve that have been

presented in literature and discussed here is shown in ﬁgure 14.

An aspect of stepping that is common to all the algorithms is the determination

of the step size. Once a converged solution for an increment has been found one

has to determine the step to use for the next increment. A popular, heuristically

derived algorithm has been proposed by Ramm [28], where the new step size ∆V

i+1

(or ∆u

i+1

, ∆Q

i+1

, S

i+1

for displacement stepping, charge stepping or path-following

respectively) is:

∆V

i+1

= ∆V

desired

realized

, (52)

where k

desired

is the desired number of steps per iteration loop and k

realized

the num-

ber of steps needed in the last converged solution step i.

A ﬁnal remark on pull-in detection. Pull-in is characterized by a singular stiffness

matrix K. This can be detected by checking if det(K) = 0. Detection is very simple

because before pull-in det(K) > 0 but once pull-in is past and the unstable solutions

331

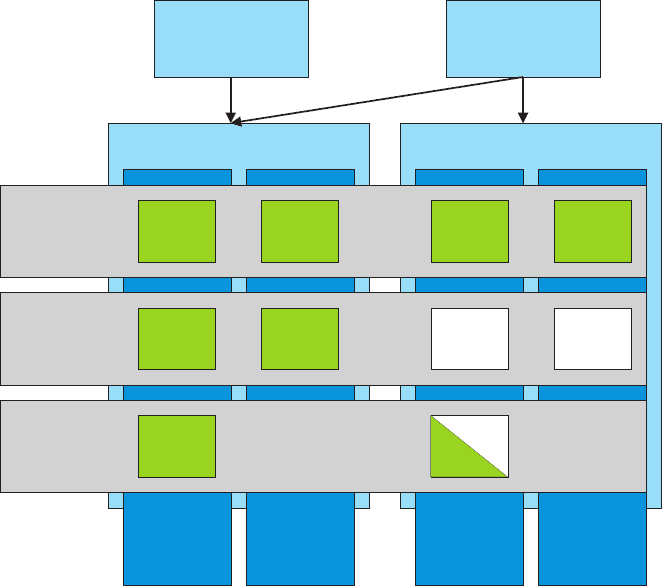
S.D.A. Hannot and D.J. Rixen

Staggered Monolithic

Co-simulation

Coupled

simulation

Voltage

control

Charge

control

Displacement

control

Without

path-following

Without

path-following

With

path-following

With

path-following

Fig. 14 Overview of the different procedures to compute the pull-in point (white squares give the

theoretically possible methods, green squares give methods realized in literature so far, the green

and white square gives a method which is explained in literature but never truly implemented in

literature)

are computed det(K) < 0. If one includes such a test after each converged iteration,

the methods can be easily enhanced with a bisection algorithm that precisely com-

putes the pull-in point. In principle this is only possible if the full coupled stiffness

matrix is available, therefore only for the coupled simulation approach. Although

hybrid methods are conceivable where a staggered method is used to compute the

equilibrium position, after which the monolithic tangent stiffness is computed at

equilibrium only for evaluation of det(K).

3.6 Example

A small comparison between the approaches is done with the model of a simple

beam. The geometry of the beam and the air gap below it is shown in ﬁg. 15. The

ﬁnite element method is used for discretization of the problem. Both domains are

332

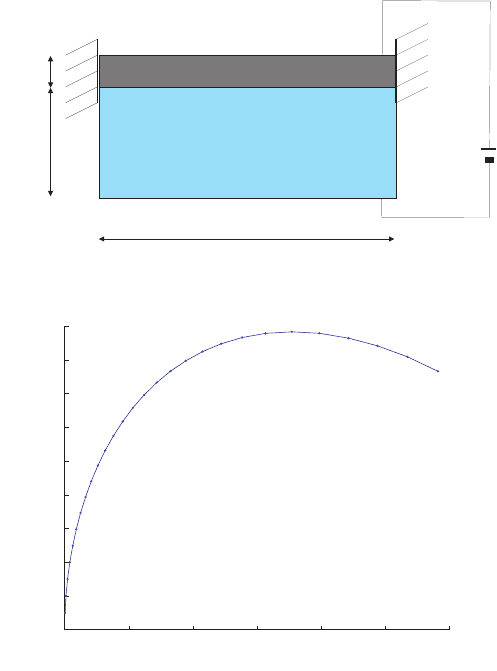
Numerical Modeling of the Electromechanical Interaction in MEMS

45µ

4µ

10µ

Fig. 15 Linear beam

0 1 2 3 4 5 6

x10

-6

Displacement (m)

Potential (V)

Fig. 16 Voltage displacement curve

meshed with quadrilaterals. The structural beam is modeled with 2D solid elements

under plane strain assumption and with linear shape functions to approximate the

displacement ﬁeld [4]. The Young’s modulus is 1 ×10

GPa and the Poisson’s ra-

tio is 0.3. The air gap is modeled with standard electrostatic elements with linear

shape functions. The vacuum electric permittivity of 8.85 ×10

−12

F/m is used to

characterize the electric domain.

The geometry of the air gap depends on the deformation of the beam, therefore

the mesh of the gap has to be updated or deformed. Here the displacements of the

nodes of the electric problem are determined by a pseudo-structure model: an elastic

stiffness matrix is assembled on the mesh of the electric problem and the deforma-

tions of the beam are applied to the pseudo structure as imposed displacements.

These displacements are used to update the coordinates of the electrostatic mesh,

inﬂuencing the electric stiffness matrix.

333

S.D.A. Hannot and D.J. Rixen

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

−5

x 10

−6

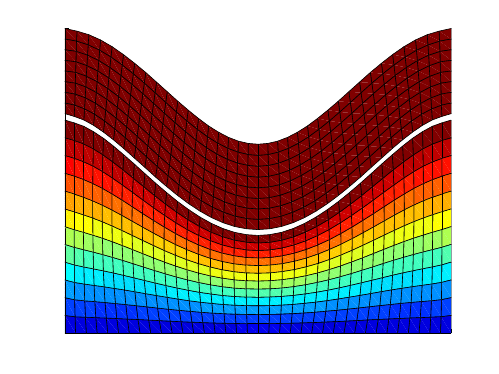
Fig. 17 Deformed shape of the simple beam

Figure 16 presents the voltage displacement curve for this beam up to a displace-

ment of 5.5µm, which is 55% of the initial air gap. The absolute displacement of

the middle node is shown. The deformed geometry of the beam and air gap at this

displacement is shown in ﬁg. 17. In this ﬁgure the beam is the part above the white

division line and the gap is the part below the line. The beam has a uniform color

and the colors in the gap indicate the potential distribution, the maximum potential

near the beam and the minimum near the grounded electrode at the bottom.

The voltage-displacement curve in ﬁg. 16 was computed with the charge loaded

block-iterative procedure, but the same results were also computed with the other

approaches. Computation times are listed in table 1. The computations were per-

formed in Matlab on a simple desktop computer (3 GHz, 2 GB RAM). The ﬁrst

thing that can be noted is that the relative error tolerance on the residual of the

structural force for the DIPIE method is less strict than that for the other methods:

this is due to the fact that it was not possible to make it converge to a relative error

below 5 ×10

−2

. The fastest of the methods that actually makes a reliable estimate

of pull-in is the charge loaded block Gauss-Seidel. Also noteworthy is the fact that

monolithic path-following with voltage control is faster than the block-iterative ver-

sion, but not faster than using charge control.

The second comparison between the approaches is presented in ﬁg. 18, which

shows the decrease of the relative error during an iteration procedure. These error

curves were determined at an increment near the pull-in point. The reason of the

fast computation time for the charge algorithm in table 1 can be easily explained

because its error curve has the steepest descent of the staggered methods. Only

the monolithic arc-length method converges faster, but it requires so much more

computation time per iteration step that the overall computation time is higher than

the charge loaded method.

334