Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Simulation of Progressive Failure in Composite Laminates

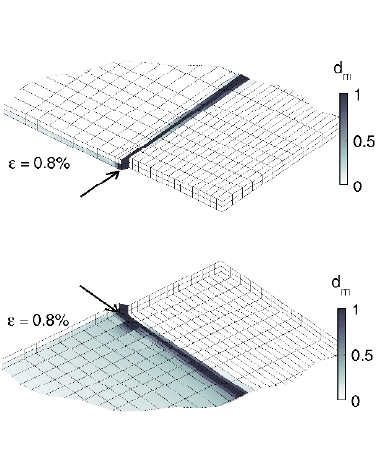
Fig. 12 Subcritical failure when realistic parameters are used for both plies with continuum dam-

age as seen from above (left) and below (right).

easily than in the real material. This we explain with the following micromechanical

considerations. A band with matrix shear failure in ﬁber direction can develop into

a macrocrack running between the ﬁbers, which is a relatively brittle mechanism,

while a band with matrix shear failure in any other direction is crossed by ﬁbers,

and the corresponding failure mechanism is therefore more ductile (see Figure 13).

In the presented continuum failure models, however, there is no inﬂuence of the

orientation of a band with matrix failure on the stress-strain behavior. A matrix

crack running between the ﬁbers (Fig. 13 (a)) is represented in the displacement

ﬁeld with localized

, and a band with matrix microcracking (Fig. 13 (b)) with

localized

, both corresponding with the same unique relation between

and

= (

)/2, while in the real material the averaged stress strain response

is different for the two mechanisms (Fig. 13 (c)). Notably, no continuum damage

models for composite materials exist which provide a solution to this problem.

A positive remark with respect to the last results can also be made, namely that

smeared degradation in the 90

◦

ply is observed, which may be understood as repre-

senting distributed matrix cracking. In the simulation results, this is clearly visible

(see Fig. 12). This is considered an appropriate mesolevel representation of the mi-

cromechanical distributed cracking, because this phenomenon is not characterized

by individual matrix cracks but rather by the quasi-homogeneousdegradation. How-

ever, the interply damage that is present around the matrix cracks on the microlevel

is not obtained in the mesomodel interface.

355

F.P. van der Meer and L.J. Sluys

Discrete crack

Damaged

band

(b)

(a)

(a) (b) (c)

Fig. 13 Micromechanical representation of matrix failure oriented in ﬁber direction (a) and matrix

failure in a band crossed by ﬁbers (b). The difference in averaged stress-strain response is illustrated

schematically (c).

2.5 Off-axis tensile test

Next, we consider an off-axis tensile test on a 10

◦

unidirectional laminate. This is a

standard test for the determination of the in-plane shear strength [9,47]. Experiments

show brittle matrix failure. In a sudden event, the specimen breaks, with the crack

running in ﬁber direction, as shown in Fig. 14. With this relatively simple example

we try to further emphasize and clarify the pathology encountered in the previous

example.

58 mm

8 mm t = 3 mm

Weak zone to initiate failure

◦

Fig. 14 Setup for off-axis tensile test and experimentally observed failure (Van Paepegem et

al. [48], used with permission from Elsevier).

Table 3 Material parameters for off-axis tensile test. Elasticity and tensile strength parameters are

taken from Van Paepegem et al. [47] (glass/epoxy).

Elasticity Ply strength Damage

38.9 GPa F

901 MPa A

100 -

13.3 GPa F

800 MPa A

3 -

0.26 -

36.5 MPa B

60 s

−1

0.4 -

70 MPa B

60 s

−1

5.13 GPa F

52 MPa

34.8 MPa

356

Simulation of Progressive Failure in Composite Laminates

A horizontal displacement is applied to the right side of the specimen, which is

free in vertical direction. Oblique ends with an angle of 54

◦

with the load direction

are used, so that for linear elasticity the stress state is homogeneous, thus eliminating

edge effects. In order to trigger localization the longitudinal shear strength F

reduced from 56 to 40 MPa in an area of 1 ×0.5 mm. Two different meshes are

used, with an in-plane element size of 0.5×0.5 mm and 0.25×0.25 mm in the area

of interest.

0 0.2 0.4 0.6 0.8 1

F (kN)

(%)

Coarse

Fine

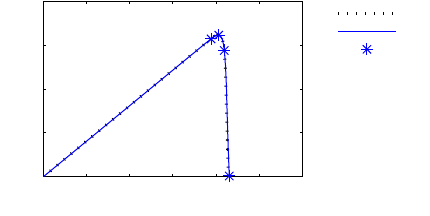
In Fig. 16

Fig. 15 Load-displacement relation for off-axis tensile test with continuum damage model and

two different meshes.

Figure 15 shows the load displacement diagram and ﬁnal deformed mesh ob-

tained with the continuum damage model. The inﬂuence of the element size on the

load-displacement behavior is sufﬁciently small, which is related to the fact that the

band with localized strain is wider than the elements, due to the viscous term. From

the deformed mesh pictures (Fig. 16), which are solutions related to the coarse mesh,

it can be observed that the failure pattern is completely different from that observed

in experiments.

Notably, there is a signiﬁcant displacement perpendicular to the load direction.

The deformation is such that the strain in ﬁber direction

remains relatively small

in the localization area. This is caused by the fact that the stiffness in ﬁber direction

remains almost completely unaffected during the analysis. This behavior stems from

the important feature that, locally, a stress state for which matrix failure may be

expected, does not give rise to a strain state which implies ﬁber failure.

However, although the local behavior is correct, the global behavior is not. The

fact that

remains small, is not sufﬁcient to obtain localized deformation aligned

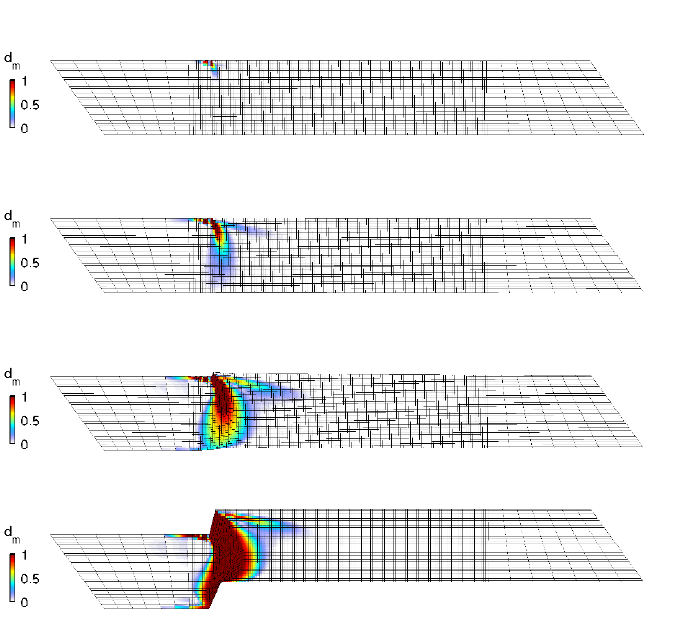
with the ﬁbers. In Fig. 16, it can be observed that, immediately when damage is ini-

tiated outside the region with reduced strength, the localization occurs at the wrong

position. There is also a band with damage which is located approximately in ﬁber

direction, but this remains secondary throughout the analysis.

The cause for this behavior lies in the fact that the direction of failure propagation

is governed by the stress concentration rather than by the ﬁber direction. This is a

consequence of the homogenization which is fundamental to the continuum models.

In the real material the failure will be contained in the weaker matrix domain, while

357

F.P. van der Meer and L.J. Sluys

Fig. 16 Evolution of matrix damage in off-axis tensile test with continuum damage (∆x =

0.25 mm).

the homogenized continuum damage model does not offer this domain separation,

as illustrated in Fig. 17. We stress that this is not resolved by distinguishing between

matrix and ﬁber failure in the degradation of the continuum, as is common practice

in continuum damage models for composite materials.

With this example, the consequences of the limitation encountered in the previous

example are clearly visible. It can be concluded that there is a fundamental problem

in the modeling of failure in composites with continuum models. The micromechan-

ical cause for cracks to grow in ﬁber direction, is not present in continuum models,

at least not as long as the model descriptions are purely local. It is unlikely that

mechanisms, in which macrocracks in ﬁber direction play a role in different plies

with different ﬁber orientation, such as the delamination failure in Fig. 2, can be

predicted using state-of-the-art continuum models for ply failure, irrespective of the

failure criteria and damage evolution laws that are applied. However, for other fail-

ure mechanisms, the continuum description might serve well, e.g. when failure in

358

Simulation of Progressive Failure in Composite Laminates

all plies is localized in a single plane [7]. In some cases the matrix crack will emerge

correctly, such as the 45

◦

crack presented by Pinho et al. [37], the split near a circu-

lar hole as reported by Cox and Yang [10] and the split in the 0

◦

-ply in the notched

plate example. But, as far as localized matrix failure in a single ply is concerned, the

predictive quality of continuum models should be doubted.

Laˇs and Zemˇcik [24] have the same difﬁculty in correctly representing cracks that

are oriented in ﬁber direction correctly. They solve it by aligning elements with the

ﬁber direction in the critical region in combination with a non-regularized material

model. Obviously, this only works when mesh-objectivity is not regarded, which

limits the predictive quality of the model.

homogen.

material

ﬁber

matrix

Fig. 17 Crack propagation in a homogeneous orthotropic medium and in a ﬁber-matrix material.

3 Phantom node method

In this section, a discontinuous representation of matrix cracking is presented. Fol-

lowing the work by Hansbo and Hansbo [17], Mergheim et al. [30] and Song et

al. [43], a crack is introduced by addition of an extra element on top of an exist-

ing element. It has been shown [43], that this method is equivalent to the extended

ﬁnite element method (XFEM) in which a discontinuity in the displacement ﬁeld

is introduced by enrichment of the shape functions with the Heaviside step func-

tion [32, 51]. With this method, we can force the crack to grow in ﬁber direction

and as such avoid the spurious mechanism encountered with the continuum damage

approach, thus incorporating the micromechanical observation that cracks tend to

grow between the ﬁbers (Fig. 17) in the mesomodel.

First the kinematic and equilibrium relations of the phantom node method are

introduced, then the applied crack propagation criterion, the constitutive relation

and the consistent tangent are discussed. The performance of the model is illustrated

with the off-axis tensile test introduced in the previous section.

3.1 Kinematical and equilibrium relations

In Fig. 18, it is illustrated how the discontinuous displacement ﬁeld is composed

of the displacements of two overlapping elements, referred to as element A and

element B. Four phantom nodes, ˜n

,.. ., ˜n

, are introduced on top of the four existing

359

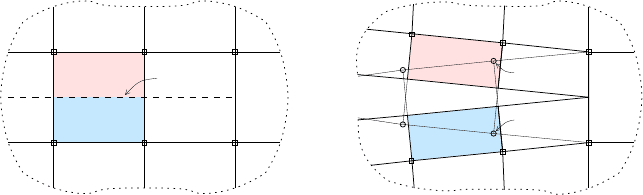
F.P. van der Meer and L.J. Sluys

nodes, n

,.. .,n

. The element domain is subdivided by a crack segment,

, into

subdomains

Ω

and

Ω

;

Ω

is corresponding with the active part of element A and

Ω

with the active part of element B. The connectivity of the overlapping elements

nodes

= [ ˜n

, ˜n

nodes

= [n

, ˜n

(19)

The displacement ﬁeld is deﬁned as

u(x) =



N(x)u

, x ∈

Ω

N(x)u

, x ∈

Ω

(20)

where N(x) are the standard ﬁnite element shape functions and u

and u

are the

nodal displacements of element A and element B, respectively. The displacement

jump over the crack is

(x) = N(x)(u

−u

), x ∈

. (21)

Ω

˜n

Fig. 18 Connectivity and active parts of two overlapping elements in phantom node method.

Figure 18 also shows that closure of the crack tip is enforced automatically, when

no phantom nodes are added on the element boundary that contains the tip.

The contribution to the nodal forces from the bulk material of the old element

(there is no conceptual difference between the old and the new element, both are

connected to some old and some new nodes and integrated over part of the original

domain, but in the code the ’old’ element is the one that has the original element

number) are computed with

bulk

Ω

(

Ω

r, (22)

with

= Bu

, (23)

360

Simulation of Progressive Failure in Composite Laminates

where

Ω

is the active part of the domain associated with the old element,

can be

any linear or nonlinear law of

, and u

are the nodal displacements associated with

the old element and B is the strain nodal displacement matrix. And similarly:

bulk

Ω

(

Ω

, (24)

with

= Bu

. (25)

The contribution to the nodal forces from the cohesive traction are computed

with

coh

(26)

and

coh

= −

. (27)

The displacement jump is deﬁned on each point x on

(x) = u

(x) −u

(x) = N(x)u

−N(x)u

. (28)

This jump may be rotated to the local frame with





= Q

, (29)

where (in 2D)

Q =



−sin

cos

sin







. (30)

3.2 Crack propagation

For the modeling of crack propagation with the XFEM or the phantom node method,

generally two criteria are needed:

• a criterion to decide whether a crack grows or not ,

• a criterion to asses in which direction the crack grows .

In the particular context of splitting in laminates, the second criterion becomes

trivial, because the propagation direction is ﬁxed, viz. equal to the ﬁber direction. To

test for propagation, the stress in the tip element is checked with a stress criterion.

361

F.P. van der Meer and L.J. Sluys

f (

) =









, (31)

which is the plane stress equivalent of Hashin’s criterion for tensile matrix failure

Eq. (6). With the operator h·i= max{·,0}compressive matrix stresses are neglected.

3.3 Cohesive law

A cohesive traction is applied on the crack surface. With this, the amount of energy

that is dissipated as the crack propagates can be controlled and the singularity in

the strain and stress ﬁeld near the crack tip is avoided. Ideally, the traction t would

be deﬁned as a function of the displacement jump

. However, the application of

a direct traction separation law for mixed mode cracking leads to computational

instability. This stems from the fact that the traction is not uniquely deﬁned for zero

crack opening; in a uni-axial case it is obvious that the traction should be equal to

the strength, but in a mixed mode formulation it can be either equal to the normal

strength with no shear traction, or to the shear strength with no normal traction,

or something in between. The traction evaluation itself is always feasible, because

after crack extension the crack opening which gives equilibrium will not be equal

to zero, but the highly nonlinear nature of the traction separation law does endanger

the stability of the Newton Raphson procedure.

However, the traction law may be constrained using equilibrium considerations.

When the bulk element that is cut by the crack segment is predominantly loaded

in tension, equilibrium demands that the traction in the crack is also predominantly

tensile traction, and when the bulk element is loaded in shear, the traction should

be shear traction. With this in mind, a new traction law, in which the bulk stress is

taken into account, has been developed by Moonen et al. [33]. This law is presented

here in adapted form.

Similar to the continuum damage model, an effective traction is computed, which

can be interpreted as the effective traction working on the reduced surface of a par-

tially cracked domain. The effective traction is deﬁned in the local frame {n,s}:

t =





= Q

n+ TQ

. (32)

When T is replaced with the acoustic tensor n

n, this effective traction can be

related to the elastic stress in the damaged cross section [33, 34]. In the present

model, however, the exact value of T is of little importance, it only serves as a

stabilization parameter. Therefore it is considered safe to use a scalar quantity T for

the sake of simplicity. For the results presented in this work, we set T equal to the

ﬁrst diagonal entry of the acoustic tensor.

In Voigt notation,

n is computed as

362

Simulation of Progressive Failure in Composite Laminates

n = H

, (33)

with (in 2D)

H =



0 n



. (34)

Notably, since the crack is parallel to the ﬁber, the vector H

contains the material

stress components

and

The bulk stress at

, which is used in Eq. (32), is not uniquely deﬁned. Indiffer-

ence to which element is labeled A and which is labeled B is maintained by comput-

ing the stress with the averaged strain:

(

), (35)

with



−



B(u

+ u

). (36)

Similar to continuum damage, the effective traction is reduced with a damage

variable (denoted

). The traction in local frame is deﬁned as:

t = [I −Ω]

t, (37)

with

Ω =





0 1





. (38)

Introduction of the factor h

, which is equal to 1 when

> 0, and equal to 0

otherwise, sufﬁces to prevent interpenetration of the cracked parts

, because with

this factor,

< 0 ⇒ t

, and, with the assumption of equilibrium (t

= (

this gives in turn t

⇒

= 0. Because equilibrium is only weakly met, limited

interpenetration may occur, but this can be expected to vanish upon mesh reﬁne-

ment.

The traction computed with Eq. (37) is rotated back to the global coordinate

frame, such that the cohesive law can be summarized as:

t = Q

[I −Ω]Q {H

+ T

}. (39)

During the failure process, the effective traction increases. The damage evolution

is driven by a state variable, denoted

which is the temporal maximum of a scalar

Provided that rotations remain small. Extension to large rotations is possible but not presented

here.

363

F.P. van der Meer and L.J. Sluys

measure for the magnitude of the effective traction:

(

) = max

t≤









. (40)

Damage variable

evolves with state variable

with the following law that

results in a linear (softening) relation between displacement jump and traction:







(

−1)

(

−1)

≥

(41)

The derivation of the expression for

will be outlined in the remainder of this

section.

We assume that the material behavior can be described properly with the phe-

nomenological relation proposed for delamination by Benzeggagh and Kenane [4],

which was applied in interface elements by Camanho, Turon et al. [6, 45]:

= G

+ (G

IIc

−G

)



+ G



, (42)

in which G

is the mode I fracture energy, G

IIc

is the mode II fracture energy,

an additional material parameter, and the ratio G

/(G

+ G

) indicates the actual

mode mixity.

We deﬁne the mode ratio

as:

+ h

. (43)

This expression can be rewritten as

i= |t

1 −

. (44)

Assuming equilibrium between the cohesive traction acting on the crack surface and

the bulk stress directly next to this surface (H

= t), it follows from Eq. (39) that

the ratio between the displacement jump components is necessarily the same:

= |

1 −

. (45)

Therefore, for a ﬁxed mode ratio

, the ratio between the energy release of the

two modes is ﬁxed:

1 −

(46)

364