Коптев А.А. Движение жидкости в центробежных полях. Ч.I. Течение жидкости вблизи вращающегося диска

Подождите немного. Документ загружается.

Рис. 1.6.12. Соотношение сбалансированного движения жидкости

на поверхности вращающегося диска при G

= –1, G(∞) = s = 1

Рис. 1.6.13. Угол между вектором скорости и касательной к окружной

при сбалансированном проскальзывании жидкости относительно

поверхности вращающегося диска

В табл. 1.6.6, наряду с другими параметрами, для анализа представлены численные значения:

•

модуль относительной безразмерной скорости на поверхности диска

(

)

(

)()

(

)()()

0000 GsGsHHU +++

′′

= ; (1.6.19)

• модуль безразмерного трения жидкости о поверхность вращающегося диска в результате относительного проскаль-

зывания

(

)

(

)()()

0000 GGHHT

′′

′′′′

= ; (1.6.20)

• угол направления векторов U и Т относительно касательной к окружностям в любой точке диска при Н(∞) = W, как

параметр

(

)

()













′

=γ

arctg

;

()













′

′′

=γ

arctg

. (1.6.21)

Графически функция угла γ в зависимости от Н(∞) = W показана на рис. 1.6.13 и табл. 1.6.6. По этой же таблице можно

проследить связь угла γ с безразмерной радиальной скоростью жидкости Н′(0) на поверхности диска.

По константам a и b возможно продолжение вычисления всех функций безразмерных скоростей и их производных при

ε ≥ ε

, которые описываются известными нам уравнениями (1.4.20), они справедливы и в рассматриваемом нами случае:

()

()()

()() ()()

()()()()

;*cos*sin

*cos*sin

K+



















ε−εβ−ε−εβ

α+



















ε−εβ

α+

+ε−εβ−

+=ε

ε−εα+−

aeWH

()

()()

(

)

(

)

[

]

;*cos*sin

K+ε−εβ+ε−εβ=ε

′

ε−εα+−

baeH

(

)

()()

(

)

(

)

[

]

,*cos*sin

K+ε−εβ+ε−εβ−+=ε

ε−εα+−

abesG

(1.6.22)

где коэффициенты α и β определяются как и прежде (1.4.10)

224

WsW ++

=α

;

224

WsW −+

=β

. (1.6.23)

Отметим, что при безразмерной аксиальной скорости Н(∞) =

= W < –0,775840 сбалансированного проскальзывания жидкости относительно поверхности вращающегося диска не сущест-

вует.

Итак, нами достаточно подробно рассмотрено течение жидкости с проскальзыванием относительно поверхности вращаю-

щегося диска в интервале изменения переменных, включающем точку L

(рис. 1.4.10) с параметрами Н(∞) = W = 0; G(∞) = s = 1;

Н′(∞) → 0; Н′′(∞) → 0; G′(∞) → 0; H′(0) = 0; G(0) = –0,603321; Н(0) = 0; Н′′(0) = –2,798630; G′(0) = 0,101782.

Теперь посмотрим на поведение жидкости при аналогичных допущениях, исходя из точки L

(рис. 1.4.1) с параметрами

Н(∞) = W = 0; G(∞) = S = –0,154200; Н΄(∞) → 0; Н′′(∞) → 0; G′(∞) → 0; H′(0) = 0; G(0) = 1; Н(0) = 0; Н′′(0) = 0,475080; G′(0) = –

0,583970.

За основу берем для численного интегрирования уравнение (1.4):

()

GHGHG

HHGHHCH

′

−

′

′′

−−

′′

′′′

где

()

∞==

GsC .

Первоначально сохраняем Н(∞) = W = 0, G(0) = 1 и изменяем s от значения его в точке L

, равного s = –0,154200 до s = –1.

Допускаем проскальзывание жидкости на поверхности диска только в радиальном направлении. Результаты расчетов показаны

на рис. 1.6.14 и в табл. 1.6.8. При состоянии противоположного направленного вращения жидкости в бесконечности и диска,

т.е. при G(∞) = s = –1 и G(0) = 1 получены величины переменных: Н′(0) = 1,124921; Н′′(0) = А = –2,118025; G′(0) =

= В = –2,042904.

Следующим этапом исследования положили условия: G(∞) = s =

= –1 = const, Н(∞) = W = 0 = const, изменяем G(0) от единицы до нуля, только радиальное проскальзывание жидкости на по-

верхности диска Н΄(0) ≠ 0; Н(0) = 0; Н′(∞) = 0; Н′′(∞) = 0; G′(∞) = 0. Графически решение показано на рис. 1.6.15 и в табл.

1.6.9. Расчеты показали, что при

W = 0 мы нашли точку М сбалансированного проскальзывания с координатами G(0) = 0,411251; Н′(0) = 0,920043. Эта точка

М на рис. 1.6.15 отмечена.

Одновременно найдена точка с координатами Н(0) = 0; Н′(0) =

= 0,726634; Н′′(0) = –1,487075; G(0) = 0; G′(0) = –0,664467; Н(∞) = W = 0; Н′(∞) → 0; Н′′(∞) → 0; G(∞) = s = –1; G′(∞) = 0, кото-

рая на рис. 1.6.15 и 1.6.1 обозначена т. Б и означает видоизменение начальных параметров движения среды в задаче Бедевад-

та при допущении радиального проскальзывания жидкости неподвижного диска.

П р и м е ч а н и е: В рассматриваемых задачах понятие "правого" или "левого" вращения не влияет на закономерности движения жид-

кости в осевом и радиальном направлениях. Если рассмотреть уравнения (1.4), (1.6.24), опять полагая

sC =

, т.е. коэффициент давления С

всегда положительный, то изменение знака на противоположный функции G(ε), и как следствие ее производных, вид уравнения (1.6.24) не

изменяет.

Проанализируем при такой ситуации, какие изменения мы должны внести в уравнения асимптотического разложения

(1.6.22) функций Н(ε); Н′(ε); G(ε) при ε ≥ ε

()

()()

(

)

(

)

[

]

;*cos*sin

K+ε−εβ+ε−εβ=ε

′

ε−εα+−

baeH

(

)

()()

(

)

(

)

[

]

.*cos*sin

K+ε−εβ+ε−εβ−+=ε

ε−εα+−

abesG

При смене знака G(ε) должны измениться знаки всех слагаемых правой части второго уравнения (1.6.22). Отметим, что

более полная запись уравнений (1.6.23) имеет вид (±):

224

WsW ++

±=α

;

224

WsW −+

±=β

В выражениях (1.6.22) величина (W + α) должна быть всегда положительной, (W + α) > 0. Значит коэффициент α всегда

положителен,

α > 0.

(1.6.24)

Поскольку G(∞) = s должен сменить знак, тогда на основании соотношения +

⋅

s должен сменить знак и параметр

β. Чтобы правая часть второго уравнения (1.6.22) изменила знак, то должен поменять знак на противоположный коэффици-

ент α. Смена знаков одновременно а и β не вносит в функции Н(ε), Н′(ε) никаких изменений.

Это свойство дифференциальных уравнений (1.4) мы использовали не только в рассматриваемом разделе, но и в целом

во всей предлагаемой работе.

Рис. 1.6.14. График радиального

проскальзывания с ростом

угловой скорости в бесконечности

G(∞) = s при безразмерной

скорости диска G(0) = 1

Рис. 1.6.15. График радиального

проскальзывания жидкости при

безразмерной окружной скорости

жидкости в бесконечности G(∞) = s = 1

в зависимости от безразмерной

скорости вращающегося диска

Случай, когда W = α = β = s = 0, нами рассмотрен в разделе 1.3.

На рис. 1.6.16 и в табл. 1.6.10 представлены значения начальных параметров Н′(0), G(0), Н(ε) = W на некотором интер-

вале изменения их величин. В других плоскостях зависимости параметров показаны на рис. 1.6.17 и 1.6.18 на основании той

же табл. 1.6.10.

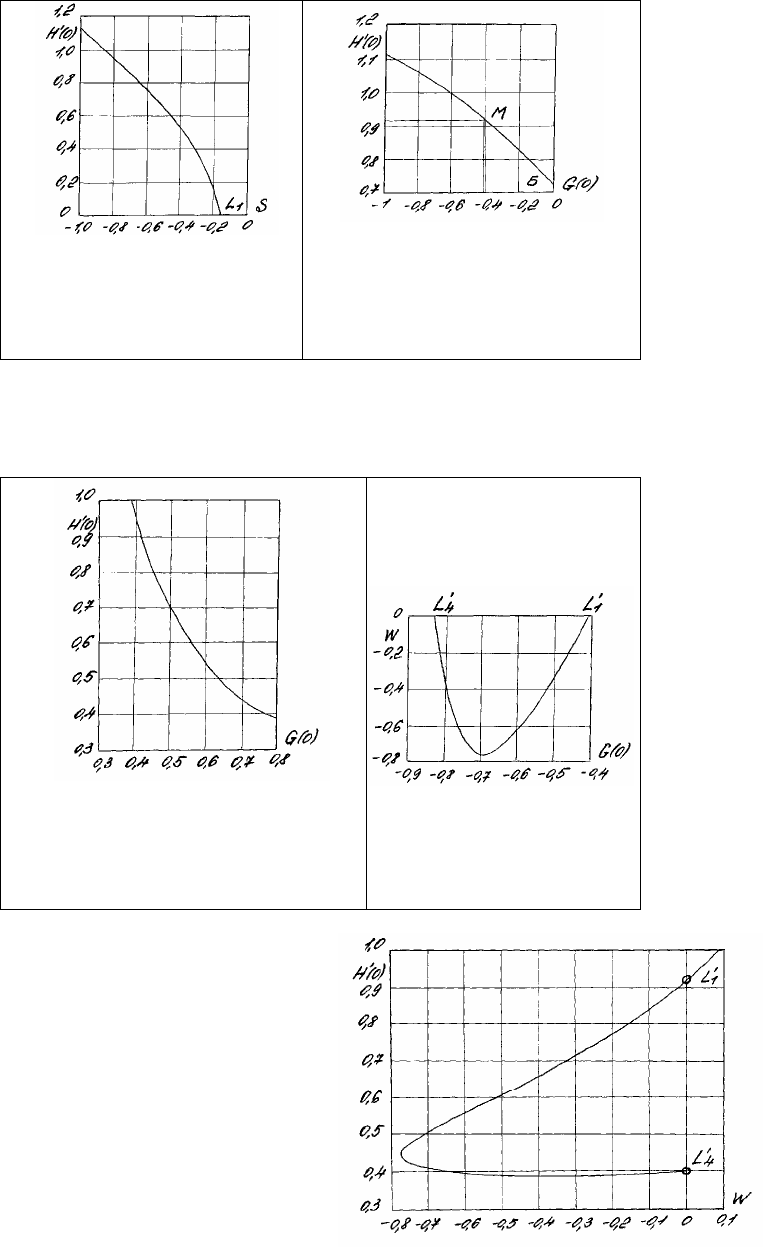
Рис. 1.6.16. График сбалансированного

радиально-тангенциального

проскальзывания жидкости

относительно поверхности

вращающегося диска в координатах G(0),

Н΄(0) и при Н(∞) = W как параметре

Рис. 1.6.17. Зависимость

сбалансированного

радиально-тангенциального

проскальзывания жидкости

при Н΄(0) как параметре

Рис. 1.6.18. Зависимость сбалансированного радиально-тангенциального

проскальзывания жидкости как функция от безразмерной осевой скорости

в бесконечности Н(∞) = W и G(0) как параметре

Анализ графиков (рис. 1.6.16 – 1.6.18) показывает, что при сбалансированном радиально-тангенциальном проскальзы-

вании жидкости на поверхности вращающегося диска Н′(0), G(0) и W взаимозависимы.

В декартовых координатах Н′(0), G(0), Н′(∞) = W эта зависимость представляет собой пространственную кривую линию,

проекции которой на координатные плоскости и показаны на рис. 1.6.16 – 1.6.18.

Замечательным является то, что эта линия точно совпадает с полученной ранее, когда мы исследование начинали исхо-

дя из точки L

. Точки L

и L

(рис. 1.4.1 и 1.4.10) соответствуют движению жидкости над вращающимся диском без про-

скальзывания при отсутствии аксиальной скорости в бесконечности, Н(∞) = W = 0. Допуская проскальзывание и вращение

диска и жидкости с одинаковыми скоростями, но противоположно направленными, G

= –1, G(∞) = s = 1, Н(∞) = W = 0, мы

получили соответственные точки L

и L

, которые отмечены на

рис. 1.6.17 и 1.6.18.

Проведем исследование проскальзывания, аналогичное ранее выполненному, взяв за исходную точку L

(рис. 1.4.1).

Она имеет параметры: Н(0) = 0; Н′(0) = 0; Н′′(0) = А = 0,490259; G(0) = 1; G′(0) =В =

= –0,561329; Н(∞) = W = 0; Н′(∞) → 0; Н′′(∞) → 0; G(∞) = s = –0,098278; G′(∞) → 0.

Будем поддерживать W = 0 = const, G(0) = 1 = const и, изменяя G(∞) = s до s = –1, интегрировать систему дифференци-

альных уравнений (1.4):

()

GHGHG

HHGHHsH

′

−

′

′′

−−

′′

′′′

допуская только радиальное проскальзывание жидкости Н′(0) по поверхности вращающегося диска. Результаты расчетов

представлены в табл. 1.6.11 и графически изображены на рис. 1.6.19. Отметим, что функция Н′(0) = f(s) проходит через мак-

симум Н′(0)

max

≈ 0,673302 при

s ≈ –0,680. По достижении G(∞) = s = –1 начальные параметры становятся Н(0) = 0; Н΄(0) = 0,601657; Н′′(0) = –3,098952; G(0) = 1;

G′(0) = –1,470749. Эти параметры точно совпадают с полученными нами ранее (табл. 1.6.1), когда мы исходной точкой брали

точку L

(с учетом выше сделанного примечания).

Дальнейшее изучение повторит уже сделанное, и мы его не проводим. Отсюда заключаем, что и в рассматриваемом

случае при сбалансированном радиально-тангенциальном проскальзывании жидкости относительно поверхности вращаю-

щегося диска начальные параметры взаимосвязаны функцией точно той же пространственной линии

(G(0), Н′(0), W) = 0.