Коптев А.А. Движение жидкости в центробежных полях. Ч.I. Течение жидкости вблизи вращающегося диска
Подождите немного. Документ загружается.


Рис. 1.6.9. Зависимость безразмерной радиальной скорости жидкости Н΄(0)
от безразмерной аксиальной скорости в бесконечности Н(∞) = W
при безразмерной окружной скорости диска G(0) = –1 и
в бесконечности G(∞) = s = 1
Сечение поверхности F(G(0), Н′(0), W) = 0 (рис. 1.6.8) по ординате G(0) = –1 показано на рис. 1.6.9 и в табл. 1.6.4 при
проскальзывании только в радиальном направлении. Отметим экстремальные значения:
W
min
= –0,736909 при H′(0) ≈ 0,667000;
Н′(0)
min
= 0,594970 при W ≈ –0,250000.
Разрез этой поверхности при
Н
΄(0) = 0 представлен графически, на рис. 1.6.10
и в табл. 1.6.5. Это фактически случай прилипания
жидкости к поверхностям диска. Минимальное значение безразмерной аксиальной скорости в этом случае Н′(0) = W = –
0,815980 при G(0) ≈ –0,28. Если окружную безразмерную скорость диска устремить G(0) → –1, то все параметры течения
жидкости в таких условиях стремятся к бесконечности. Еще раз упоминаем, что решение задачи без проскальзывания при
G(0) = –1 и G(∞) = s = 1 невозможно. На рис. 1.6.10 показаны вышеобозначенные точки L
4
и Б. Если двигаться по поверхности
F(G(0), Н′(0), W) = 0 рис. 1.6.8 по линии точек М, М, …, М, то получаем картину изображенную на рис. 1.6.11 и в табл. 1.6.6.
Экстремальные значения переменных при этом:
W
min
= –0,775840 при H′(0) = 0,445420; G(0) = –0,6907;
Н′(0)
min
= 0,390126 при W ≈ –0,350000; G(0) = –0,798972.
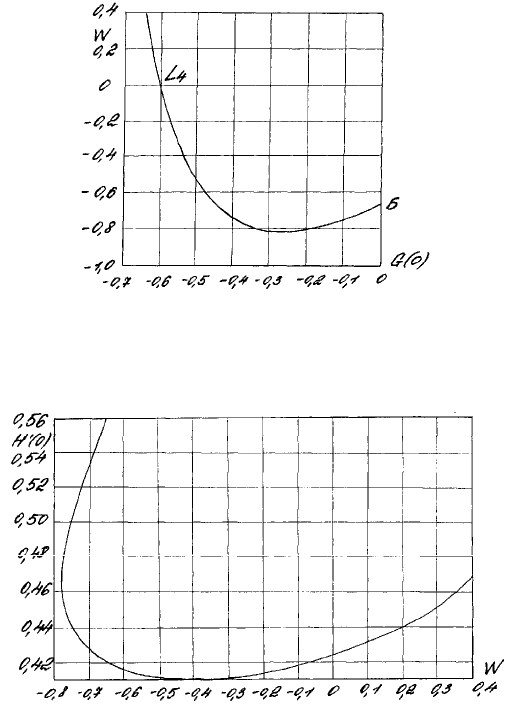
Рис. 1.6.10. Связь осевой безразмерной скорости жидкости
в бесконечности Н(∞) = W с безразмерной окружной скоростью диска G(0), в бесконечности G(∞) = 1 в случае отсутствия проскаль-
зывания жидкости относительно поверхности диска
Рис. 1.6.11. Сечение поверхности рис. 1.6.8 по линии М, М, …, М
На рис. 1.6.12 изображено соотношение сбалансированного движения жидкости по поверхности вращающегося диска,
вращающегося с безразмерной скоростью G
д
= –1, в бесконечности среда имеет скорость G(∞) = 1 (кривая 1). Там же приве-
дено предельное значение
Н(∞) = W = –0,775840, при котором сбалансированность (кривая 2) существует в одной точке N. Точка N соприкосновения
кривых 1 и 2 имеет координаты Н′(0) = 0,445420, G(0) = –0,6907, W = –0,775840.
Данные для построения кривой 2 содержатся в табл. 1.6.7.
