Коптев А.А. Движение жидкости в центробежных полях. Ч.I. Течение жидкости вблизи вращающегося диска
Подождите немного. Документ загружается.

А.А. Коптев
ДВИЖЕНИЕ ЖИДКОСТИ
В ЦЕНТРОБЕЖНЫХ
ПОЛЯХ
Ч а с т ь I
ТЕЧЕНИЕ ЖИДКОСТИ
ВБЛИЗИ ВРАЩАЮЩЕГОСЯ ДИСКА
МОСКВА
"ИЗДАТЕЛЬСТВО МАШИНОСТРОЕНИЕ-1"
2005

А.А. Коптев
ДВИЖЕНИЕ ЖИДКОСТИ
В ЦЕНТРОБЕЖНЫХ
ПОЛЯХ
Ч а с т ь I
ТЕЧЕНИЕ ЖИДКОСТИ
ВБЛИЗИ ВРАЩАЮЩЕГОСЯ ДИСКА
МОСКВА
"ИЗДАТЕЛЬСТВО МАШИНОСТРОЕНИЕ-1"
2005
УДК 532
ББК В253.31
К658
Рецензенты:
Доктор технических наук, профессор
М.Б. Генералов
Кандидат технических наук, профессор
А.С. Клинков
Коптев А.А.
К658 Движение жидкости в центробежных полях. Ч. I. Течение жид-
кости вблизи вращающегося диска. М.: "Издательство Машино-
строение-1", 2005. 240 с.
Представлено фундаментальное исследование гидродинамики: дви-
жение жидкости вблизи вращающихся поверхностей дисков. Разработан
ряд программ численного интегрирования уравнений Навье-Стокса в
цилиндрической системе координат. Рассмотрены решения течений в
пограничных слоях при различных граничных условиях.
Для инженерно-технических работников, занимающихся проектиро-
ванием центробежных аппаратов, а также научных сотрудников, аспи-
рантов. Может быть полезна студентам технических вузов.
УДК 532
ББК В253.31
ISBN 5-94275-180-3
© Коптев А.А., 2005
© "Издательство Машиностроение-1",
2005
Научное издание
КОПТЕВ Андрей Алексеевич
ДВИЖЕНИЕ ЖИДКОСТИ
В ЦЕНТРОБЕЖНЫХ ПОЛЯХ
Ч а с т ь I
ТЕЧЕНИЕ ЖИДКОСТИ ВБЛИЗИ ВРАЩАЮЩЕГОСЯ ДИСКА
Монография
Редактор З. Г. Ч е р н о в а
Инженер по компьютерному макетированию М. Н. Р ы ж к о в а
Подписано к печати 18.04.2005.
Формат 60
× 84/16. Гарнитура Times. Бумага офсетная. Печать офсетная.
Объем: 13,95 усл. печ. л.; 14,05 уч.-изд. л.
Тираж 100 экз. С. 227
М
"Издательство Машиностроение-1",
107076, Москва, Стромынский пер., 4
Подготовлено к печати и отпечатано в издательско-полиграфическом центре
Тамбовского государственного технического университета
392000, Тамбов, Советская, 106, к. 14

ВВЕДЕНИЕ
В разных отраслях промышленности в технологических процессах и аппаратах для интенсификации гидромеханики, тепло-
и массообмена используются центробежные силы. Это – центрифугирование, сепараторы, центробежные распылители и раз-
брызгиватели, центробежные насосы, ротационные абсорберы и теплообменники и др. В природе преобладает явление враща-
тельного движения сплошной среды. Поступательное, прямолинейное движение – это частный случай на ограниченном участке
линии движения, либо искусственно организованный человеком. Природа не "любит" прямолинейности. Конкурентом является
колебательное движение, которое также циклическое, как и круговое движение.
В природе центробежные движения вечны кроме нами упомянутых случаев в технике. Мы наблюдаем смерчи, торнадо,
тайфуны, циклоны в атмосфере, водовороты в реках и океанах и знаем, что вращение макрокосмических объектов – это ус-
тойчивое состояние материи, микромире – это то же самое (Spin).
В предлагаемой работе мы рассмотрим узкий круг задач, связанных с движением сплошной вязкой среды в различных
технически и конструктивно организованных устройствах вблизи гладких вращающихся дисков (конусов) с различными
граничными условиями.
Мы не ставим целью обзор многочисленных работ в этом направлении, а будем ссылаться только на классические. Представим
только наши изыскания, которые являются скромным дополнением к тем знаниям, которые были получены достойными исследова-
телями в рассматриваемой области.
За основу теоретических исследований положим уравнения Навье-Стокса
[1], [2] в цилиндрической системе координат r, ϕ, z в
общем виде
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
+−
∂
∂
+
∂
∂
+
+
∂
∂
−=
∂
∂
++
∂
∂
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
−
∂
∂
+−
∂
∂
+
∂
∂
+
+
∂
∂
−=
∂
∂
+−
∂
∂
+
∂
∂
+
∂
∂
2
2
2
2
22
2
2
2
22
2
222
2
2
2
22
2
222
2
2
11
1
;
v2v1vv1v
1vvvvvv
;
v211
1vv
z
ww
rr
w
rr
w
z
p
F
z
w
w
w
r
v
r
w
u
t
w
z
u
rrrrrr
p
r
F
z
w
r
u
rr
u
t
z
u
r
u
rr
u
r
u
rr
u
r
p
F
z
u
w
r
u
rr
u
u
t
u
z
r
ϕ
ν
ρϕ
ϕϕ
ν
ϕρϕ
ϕϕ
ν
ρϕ
ϕ
(1)
и уравнение неразрывности для несжимаемой жидкости
0
1
=
∂
∂
+
ϕ∂
∂
++
∂
∂
z
wv
rr
u
r
u
, (2)
где u, v, w – соответственно радиальная, окружная и осевая составляющие скорости; ν – кинематическая вязкость жидкости;
ρ – плотность жидкости; F
r
, F
ϕ
, F
z
– проекции массовых сил на оси координат; t – время; p – давление.
В дальнейшем будем рассматривать установившееся движение. Тогда производные по времени равны нулю,
0=
∂
∂
t
.
При осесимметричном движении производные по координате ϕ также будут равны нулю,
0=
ϕ∂
∂
. Кроме того, логично по-
ложить для рассматриваемых задач, что массовые силы F
r
= F
ϕ
= F
z
= 0.
При таких условиях уравнения (1), (2) принимают вид:
=
∂
∂
++
∂
∂
∂
∂
+
∂
∂
+
∂
∂
ν+
∂
∂
ρ
−=
∂
∂
+
∂
∂
∂
∂
+−
∂
∂
+
∂
∂
ν=
∂
∂
++
∂
∂
∂
∂
+−
∂
∂
+
∂
∂
ν+
∂
∂
ρ
−=−
∂
∂
+
∂
∂
.0
;
11
;
vvv1vvvv
;
11v
2
2
2
2
2
2
22
2
2
2
22
22
z
w
r
u
r
u
z
w
r
w
r
r
w
z
p
z
w
w
r
w
u
zr
rr
r
z
w
r
u
r
u
z
u
r
u
r
u
r
r
u
r
p
rz
u
w
r
u
u
(3)
Известны несколько аналитических решений дифференциальных уравнений (3), например, движение жидкости в трубе,
течение в зазоре между вращающимися цилиндрами. В большинстве случаев необходимо численное интегрирование, кото-
рое мы использовали в своих исследованиях.
1. ТЕЧЕНИЕ ЖИДКОСТИ
ВБЛИЗИ ВРАЩАЮЩЕГОСЯ ДИСКА
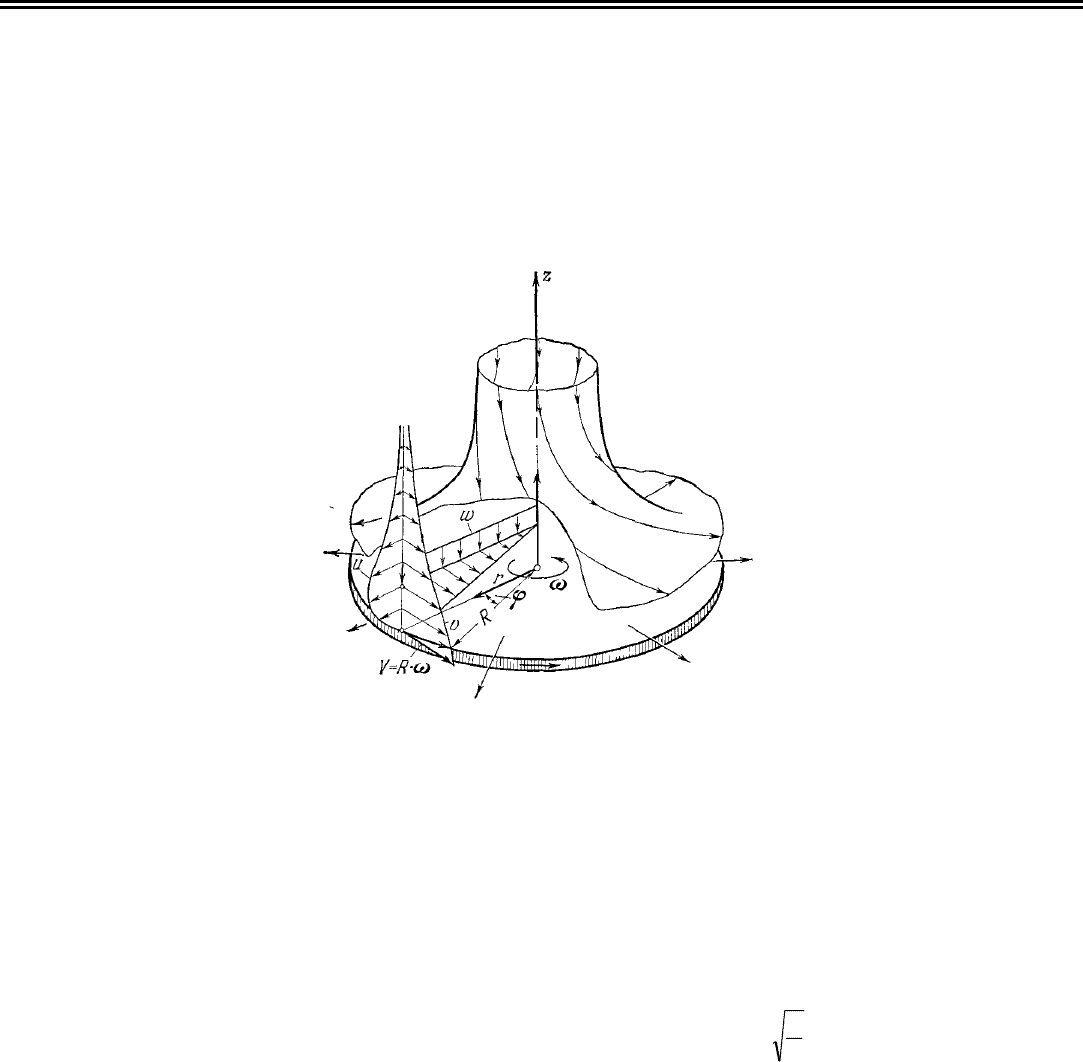
Примером точного решения уравнений Навье-Стокса является течение вблизи плоского диска, равномерно вращающе-
гося с угловой скоростью ω вокруг оси, перпендикулярной к плоскости диска. Жидкость вдали от диска принимаем покоя-
щейся. Вследствие трения слой жидкости, непосредственно прилегающий к диску, увлекается последним и под действием
центробежной силы отбрасывается наружу от диска. Взамен отброшенной жидкости к диску притекает в осевом направле-
нии новая жидкость, которая также увлекается диском и опять отбрасывается наружу. Следовательно, в данном случае мы
имеем полностью трехмерное течение. Перспективное изображение этого течения показано на рис. 1.1.
Вычисления выполним сначала для неограниченной вращающейся плоскости, после чего, пренебрегая концевым эф-
фектом, перенесем полученный результат на случай круглого диска, имеющего конечный диаметр D = 2R.
Рис. 1.1. Течение в окрестности диска,
вращающегося в покоящейся жидкости
Для рассматриваемой задачи справедливы уравнения (3).
Граничные условия, с одной стороны, определяются условиями прилипания к вращающейся поверхности и непрони-
цаемостью диска
0
=
u ,
r
ω
=
v
, 0=w при 0=z ; (1.1)
с другой стороны, при z, равном некоторой конечной величине z
0
(или бесконечности), в зависимости от рассматриваемой
задачи могут принимать различные выражения. Для интегрирования системы уравнений (3) удобно ее привести к безразмер-
ному виду. Примем вместо z безразмерное расстояние от поверхности диска
ν
ω
=ε z
. (1.2)
Также примем, что составляющие скорости и давления определяются формулами

(
)
()
()
()
ερων−
ρω
−=
εων−=
εω=
ε
′
ω=
,2
2
;2
;v
;
22
P
r
Cp
Hw
rG
Hru
(1.3)
где С – постоянная, подлежащая численному определению в результате интегрирования уравнений (1.4) при конкретных
граничных условиях.
В результате подстановки выражений ε, u, v, w, p по уравнениям (1.2) и (1.3) в систему уравнений (3) получим три диф-
ференциальных уравнения для определения неизвестных функций Н, G, Р:
()
′
+
′′
=
′
′
−
′
=
′′
′′
−−
′′
+=
′′′
,2
;2
;2
2
HHHP
GHGHG
HHGHHCH
(1.4)
где ′, ″, ′′′ – соответствующие производные по ε.
Уравнение неразрывности системы (3) при этом удовлетворяется тождественно.
Граничными условиями системы уравнений (1.4), вместо условий (1.1), будут
()
0,1,00 РРGH,H =
=
=
′
=
при 0=ε . (1.5)
Примем на внешней границе
sGH =
=
′
,0 при
0
ε
=ε . (1.6)
Решение системы дифференциальных уравнений (1.4) при ε
0
→ ∞, С = 0, s = 0 впервые приближенным способом было
получено Т. Карманом [3], уточнено впоследствии В. Кохреном [4] посредством разложения функций Н и G в степенные
ряды при ε = 0 и асимптотического разложения при больших значениях ε и их смыкании при некотором среднем значении ε
*
.
Представим вышеуказанные разложения функций системы (1.4).
Для разложения функций Н и G в степенные ряды Тейлора продифференцируем первые два уравнения системы (1.4) п
раз:
(
)
()
()
(
)
..................
;34
332
;322
;2
;2
IIIIIIII
IVIIIIIIIVIIVIVIVII
IIIIIIIIIIIIVIVVI
IIIIIIIIIVV
IIIIIV
GGGG
GGHHHHHHHHH
GGGGHHHHHHH
GGGGHHHHH
GGHHH
++
+++++−=
++++−=
+++−=
+−=
(
)
()
()
()
()
..................
;45542
;32232
;222
;2
;2
VIVIIVIIIIIVIVVIVII
VIVIIIIIIIIIIIIIVVVI
IVIIIIIIIIIVV
IIIIIIIIIIIIIV
IIIIIII
HGGHGHGHGHGHG
HGGHGHGHGHGHG
HGGHGHGHG
HGGHGHGHG
HGGHG
−−−++=
−−−++=
−−+=
−−+=
−=
(1.8)
Имея в виду граничные условия в начале координат (1.5) и обозначив
(
)
AH =0
II
,
()
BG =0
I
, после поочередной под-
становки их в уравнения (1.4), (1.7) и (1.8) получим:
(1.7)
()
()
()
() ( )
()
()
()
()
()
()
()
()
()
()
()
()
() ( )
()
()
()
()
()
+++−−=
−++−=
−−−=
−−=
+−=
−+=
=
=
=
=
++−+=
+−+−=
+−=
−−−=
−−=
−=
−=
−=
=
=
=
.............
;3202482241361680
;164024112880
;201624160
;8160
;480
;1220
;20
;00
;0
;00
..............
;144112232104880
;40444240
;48160
;1280
;220
;20
;20
;10
;0
;00
;00
232IX
2VIII
23VII
22VI
V
IV
III
II
I
223X
2222IX
2VIII
2VII
VI
2V
IV
III
II
I
BCABABCBG
CCBACABG
BABACAG
ABG
BCBG
CABG
AG
G
BG
G
ACBAACABH
CACBBAH
ABBCBH
CABH
ACAH
BH
BH
CH
AH
H
H
Разложения функции Н (ε) и G (ε) около ε = 0 в степенные ряды Тейлора
() ()
(
)
(
) () ()
() ()
() ()
()
() () ()
()
() ()
()
() () ()
()
+ε+
+ε+ε+ε+ε+=ε
+ε+
+ε+ε+ε+ε+=ε
+ε+ε+
+ε+ε+ε+ε+=ε
.
!5
0
!4
0
!3
0
!2
0
!1
0
0
;
!5
0
!4
0
!3
0
!2
0
!1
0
0
;
!6
0
!5
0
!4
0
!3
0
!2
0
!1
0
0
5
V
4
IV
3
III
2
III
5
VI
4
V
3
IV
2
IIIII
II
6
VI
5
V
4
IV
3
III
2
III
K
K
K
G
GGGG
GG
H
HHHH
HH
HH
HHHH
HH
(1.10)
Подстановка выражений (1.9) в (1.10) при С = 0 приводит к следующим выражениям рядов разложения:
(1.9)

()
()
()
+ε
−+
+
+ε
−
+ε
−−
+
+ε
+
−ε−ε
−
+ε+ε+=ε
+ε
++
+
+ε
−
+ε
+
+
+ε
−
+ε−ε−ε−ε−ε=ε
+ε
++
+
+ε
−
+ε
+
+
+ε
−
+ε−ε−ε−ε−ε=ε
.
!9
168248224
!8
1688
!7
201616
!6
816
!5
8
!4
22
!3
2
1
;
!9
11210488
!8
2444
!7
416
!6
82
!5
2
!4
2
!3
2
!2
1
;
!10
11210488
!9
2444
!8
416
!7
82
!6
2
!5
2
!4
2
!3
1
!2
9
23
87
23
6
22
543
9
23
8
22
7
2
654
2
32I
10
23
9
22
8
2
765
2
432
K
K
K
BABA
ABBABA
ABBABA
BG
BAAB
ABABB
ABABB
AH
BAAB
ABABB
ABABBA
H
1.1. ТЕЧЕНИЕ ЖИДКОСТИ ВБЛИЗИ
ВРАЩАЮЩЕГОСЯ ДИСКА ПРИ ОТСУТСТВИИ
ГРАДИЕНТА ДАВЛЕНИЯ ВДОЛЬ РАДИУСА
Рассмотрим разложение функций Н и G в асимптотические ряды при С = 0 и значительных величинах ε. Проанализиру-
ем первые два уравнения системы (1.4):
()
′
−
′
=
′′
′′
−−
′′
+=
′′′
.2
,2
2
GHGHG
HHGHHCH
(1.1.1)
Граничные условия рассматриваемой задачи при ε → ∞, Н′ → 0,
G → 0, Н → Н
∞
→ W, где W – значение безразмерной аксиальной скорости Н в бесконечности, т.е. на достаточно большом
удалении от поверхности диска. Значения функций малы, за исключением Н. Значит члены уравнений (1.1.1) Н′Н′, G
2
, Н′G
второго порядка малости в сравнении с остальными слагаемыми. Можем записать
HGGHHH 2,2
−
=
′
′
′
′
−
=
′
′
′
или
WGGHWH 2,2 −=
′′
′
′
−
=
′
′
′
. (1.1.2)
После интегрирования (1.1.2) получим
ε−ε−
=
′
=
′′
WW
ebGeaH
2
0
2
0
,
, (1.1.3)
где а
0
, b
0
– постоянные интегрирования.
Последующее интегрирование (1.1.3) приводит к выражениям
ε−
−
=
′
W
e
W
a
H
2
0
2
,
ε−
+=
W
e
W
a
WH
2
2
0
4
,
ε−
−
=
W
e
W
b
G
2
0
2
.
Обозначив
W
a
a
2
0
−= ,
W
b
b
2
0
−= , окончательно в первом приближении имеем
ε−
−=
W
e
W
a
WH
2
2
;
ε−
=
′
W
aeH
2
,
ε−
=
W
beG
2
; (1.1.4)
ε−
−=
′′
W
aWeH
2
2 ,
ε−
−=
′
W
bWeG
2
2 .
Вторые члены разложения находим из соотношений, вытекающих из (1.4):
HHGHHHWH
′′
−−
′′
=
′′
+
′′′
22
2
11
;
GHGHGWG
′
−
′
=
′
+
′
′
222
11
.
(1.11)

Значения членов правой стороны
()
()
()
.02
2
222
;2
2
22
4
11
422422
11
=
−
−−=
′
+
′′
−−=
−−−=
′′
+
′′′
ε−
ε−ε−
W
WW
eWb
W
a
abGWG
ebaeaW
W
a
baHWH
(1.1.5)
Следует найти частные решения дифференциальных уравнений (1.1.5). Обозначим
ε−
=
′′′
W
DeH
4
1
,
тогда
ε−
−=
′′
W
e
W
D
H
4
1
4
.
Подставим это в первое уравнение (1.1.5)
(
)
WW
ebae
W
D
WD
4224
4
2
−ε−
+−=
−+ ,
откуда
(
)
22
2 baD +−=
и
(
)
ε−
+−=
′′′
W
ebaH
422
1
2
.
После интегрирования последнего уравнения получим:
ε−
+
=
′′
W
e
W
ba
H
4
22
1
2
,
ε−
+
−=
′
W
e
W
ba
H
4
2
22
1
8
,
ε−
+
=
W
e
W
ba
H
4
3
22
1
32
. (1.1.6)
Из второго уравнения (1.1.5) видим, что
0
1
=G . (1.1.7)
По аналогии третьи члены разложения найдем из выражений
.22222
;222
111122
11111122
GHGHGHGHGWG
HHHHGGGGHHHHHWH
′
−
′
−
′
+
′
=
′
+
′′
′′
−
′′
−−−
′′
+
′′
=
′′
+
′′′
(1.1.8)
Подстановка в правую часть уравнений (1.1.8) значений функций по (1.1.4), (1.1.6) и (1.1.7) приводит к выражениям
(
)
ε−
+
=
′′
+
′′′
W
e
W
baa
HWH
6
2
22
22
8
3
2
;
(
)
ε−
+
−=
′
+
′′
W
e
W
bab
GWG
6
2
22
22
8
2
. (1.1.9)
Частными решениями дифференциальных уравнений (1.1.9) являются
(
)
ε−
+
−=
W
e
W
baa
H
6
5
22
2
384
;
(
)
ε−
+
=
′
W
e
W
baa
H
6
4
22
2
64
;
(
)
ε−
+
−=
′′
W
e
W
baa
H
6
4
22
2
32
3
;
(
)
ε−
+
−=
W
e
W
bab
G
6
4
22
2
192
;
(
)
ε−
+
=
′
W
e
W
bab
G
6
3
22
2
32
. (1.1.10)
Следующие члены асимптотического разложения функций Н, G найдем из решения уравнений
[]
.22
;222
2
1122112233
1122112
2112233
GHGHGHGHGHGHGWG
HHHHHHGGGG
GGHHHHHHHWH
′
−
′
−
′
−
′
+
′
+
′
=
′
+
′′
′′
−
′′
−
′′
−−−
−−
′′
+
′′
+
′′
=
′′
+
′′′
(1.1.11)
Используя значения функций (1.1.4), (1.1.6), (1.1.7) и (1.1.10), приводим уравнения (1.1.11) к виду
(
)
(
)
()
.
24
2
;
192
17
2
8
4
22
33
8
4
2222
33
ε−
ε−
+
=
′′
+
′′
++−
=
′′
+
′′′
W
W
e
W
baab
HWG
e
W
baba
HWH
(1.1.12)
