Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

We find

We use that f

/ p is constant along the trajectory. Consider this in more detail.

The distribution function f

depends on the variables p

, , b, where p

is the

momentum along the z-axis. The momentum derivative

/ p can be presented

(14.40)

The plus sign is for quasi-electrons while the minus sign is for quasi-holes, since

the directions of v

and p are either the same or opposite for these two types

of quasiparticles, respectively. The terms

/ p and f

/ in eqn (14.40) are

indeed constant along the trajectory but the term

/ b is not. However, one

can show that this term vanishes identically for an axisymmetric vortex in

s-wave superconductors. We shall prove this later in Section 15.3 in a more

general form.

The collision integral can be also presented as a spectral sum

(14.41)

end p.283

because it contains terms proportional to either g or . The

kinetic equation becomes

(14.42)

where ail terms are taken, at =

The term f

/ p in eqn (14.42) should be

now understood as

(14.43)

The component in eqn (14.40) parallel to v drops out of eqn (14.42).

14.4.1.1 Low temperatures

The integro-differential equation (14.42) can hardly be solved analytically in a

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:08

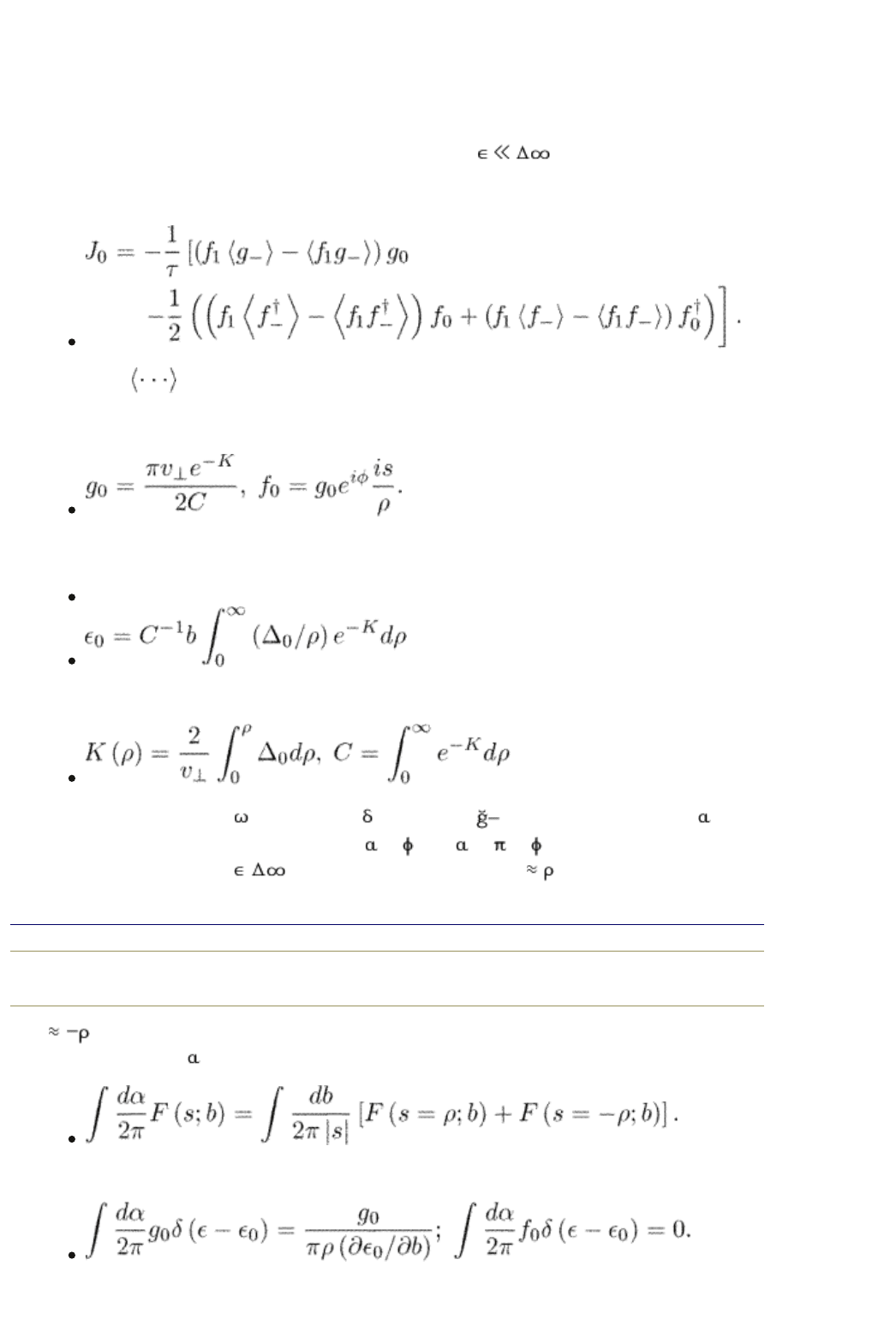
general case. Some simplifications arise when temperatures are much below T

Only the level with n = 0 is excited at such temperatures. The corresponding

solution was first obtained by Kopnin and Kravtsov (1976 a). For simplicity, we

restrict ourselves to a spherical Fermi surface.

We assume that the scattering by impurities is the primary source of relaxation.

This is the most natural assumption for practically all superconducting materials.

Consider the impurity collision integral for energies

. The spectral weight

for n = 0 in the expansion eqn (14.41) of the collision integral can be found from

eqn (10.74). It has the form

Recall that is the usual average over the Fermi surface. The Green

functions for low energies were found, in Section 8.4. According to eqn (6.83)

the spectral weights are

The bound state energy is given by eqn (6.84).

(14.44)

where

and we neglect a small

. Due to the -function in , the integration over d

selects a narrow region of angles near = and = + such that the impact

parameter is small b ~

/ and the distance is either s or

end p.284

s , respectively. Calculating the Fermi-surface averages we will perform the

integration over d

using the rule

As a result

Let us take the distribution function in the form of eqn (14.9) and consider the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:08

collision integral. Performing the averaging, we have

and

Here we omit contributions proportional to small b. Using

we obtain for the collision integral

(14.45)

where denotes the operator

The integral is logarithmic; the divergence is cut off at ~ ( / ) .

To solve the kinetic equation we insert this into eqn (14.42) and find the

expressions for

and

in terms of the vortex velocity. These expressions also

contain the averages

Next, we average

and

with the weight p /C (

/ b), solve the

obtained equation for these averages, and exclude thorn from expressions for

and

. This completes the calculation of

and

end p.285

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:08

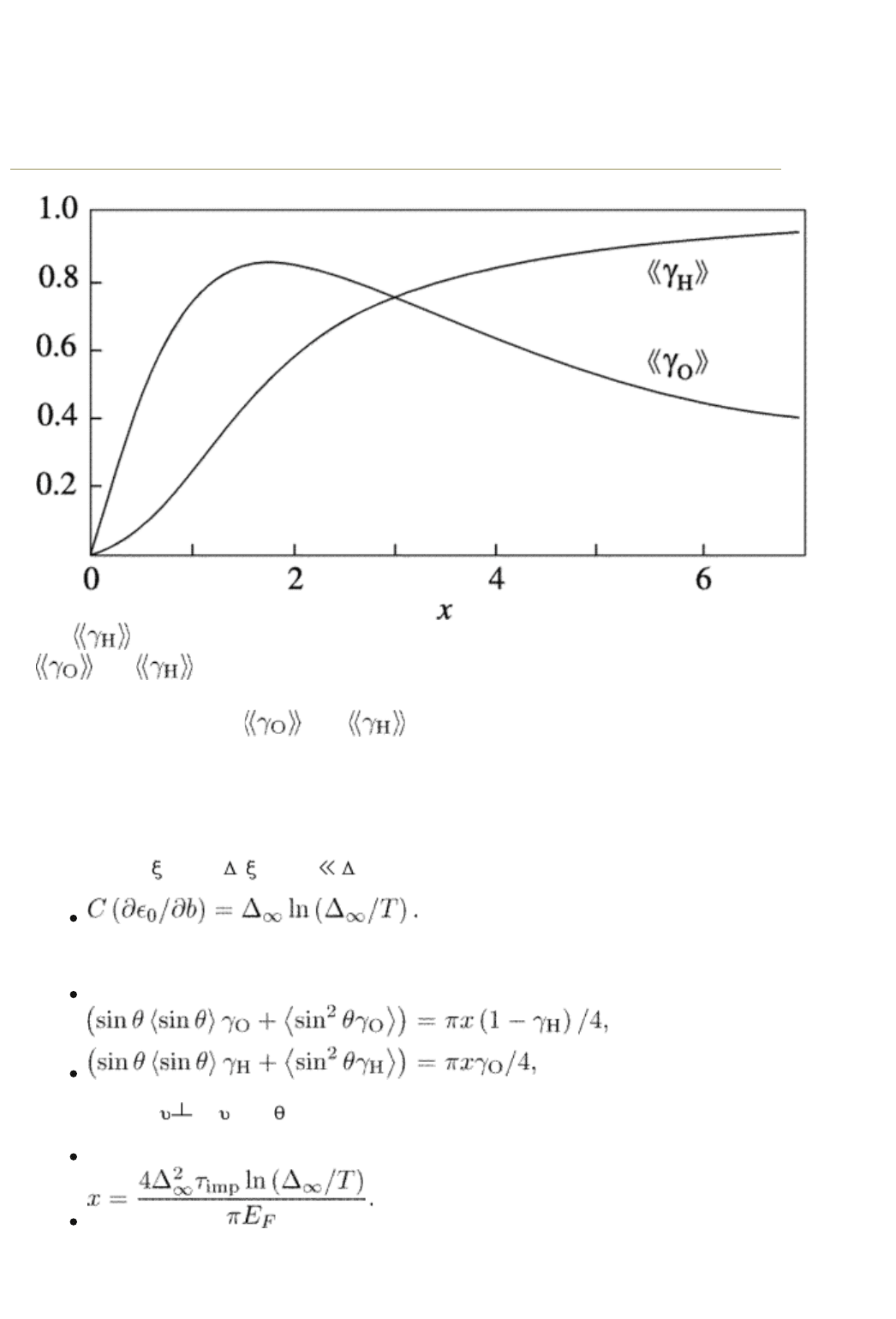
and as functions of the purity parameter x." title="Fig. 14.1. The factors

and as functions of the purity parameter x." class="figure">

IG. 14.1. The factors and as functions of the purity

parameter x.

This general scheme of calculations can be carried out explicitly if we make use

of the so-called Kramer-Pesch effect: the compression of the vortex core at low

temperatures. According to Kramer and Pesch (1974) the size of the vortex core

decreases as

~ (T/ )

for T . In this case one has from eqn (14.44)

Equation (14.42) yields a set of equations

(14.46)

where we put =

sin and

(14.47)

One finds from equations (14.46)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [286]-[290]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 16:09

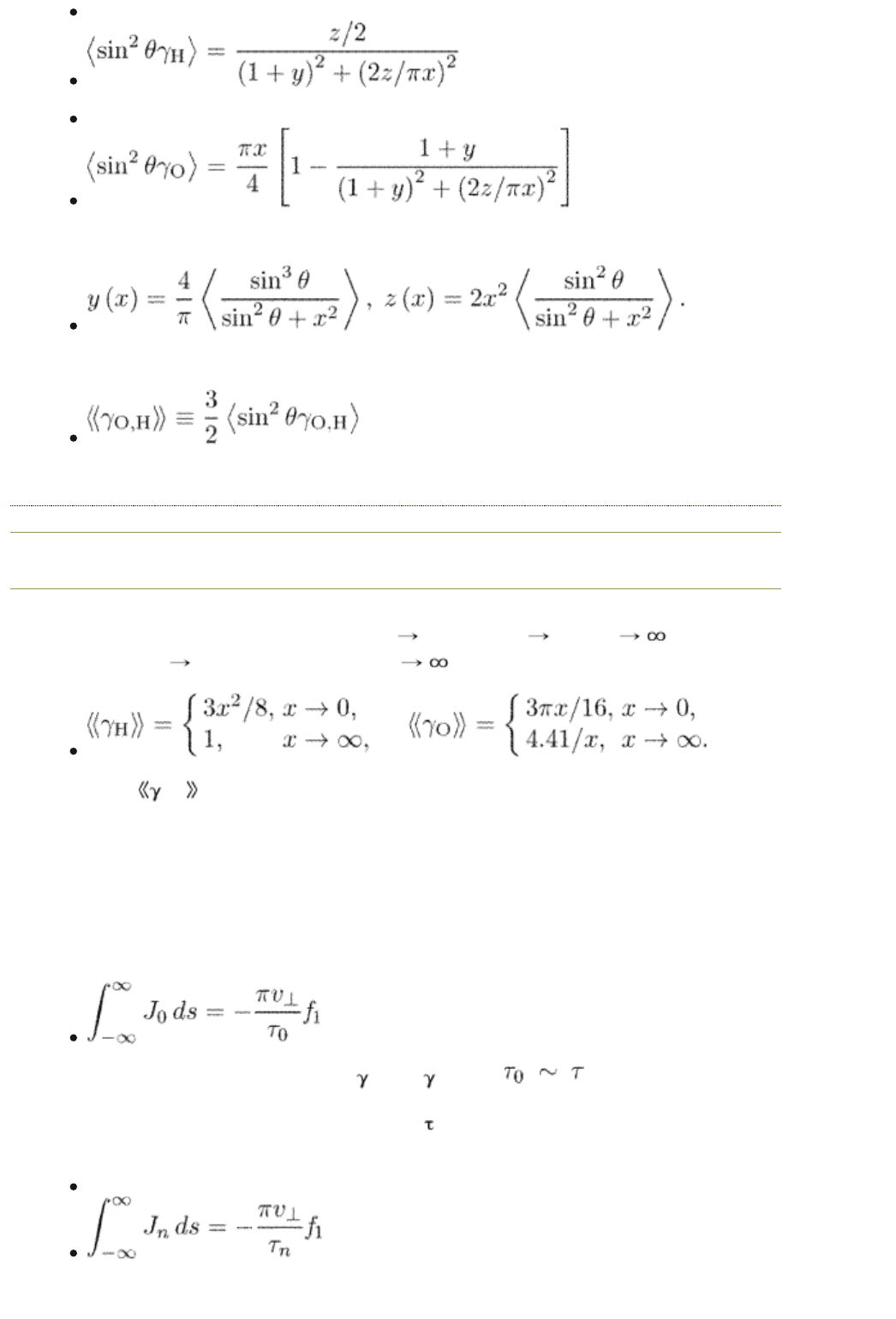
(14.48)

(14.49)

where

We shall see later that these are the values

end p.286

which are needed to calculate the corresponding components of the flux flow

conductivity. The function y (x) = 1 for x

0 and y (x) 0 for x while z

(x) = 2x

for x 0 and z (x) = 4/3 for x . Correspondingly,

The factors

O,H

are plotted in Fig. 14.1 as functions of the purity parameter x.

14.4.1.2 Relaxation-time approximation, arbitrary temperatures

The solution of the kinetic equations obtained for low temperatures by Kopnin

and Kravtsov (1976 a) can be generalized to arbitrary temperatures (Kopnin and

Lopatin 1995). To do this we need to simplify the collision integral. Inspection of

eqn (14.45) shows that the collision integral takes the form

if one neglects the p

dependence of

and

. Here is some effective

relaxation time for the low-energy level. To generalize our consideration for

temperatures not much below T

we adopt a -approximation for the collision

integral. We assume that

(14.50)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 16:09

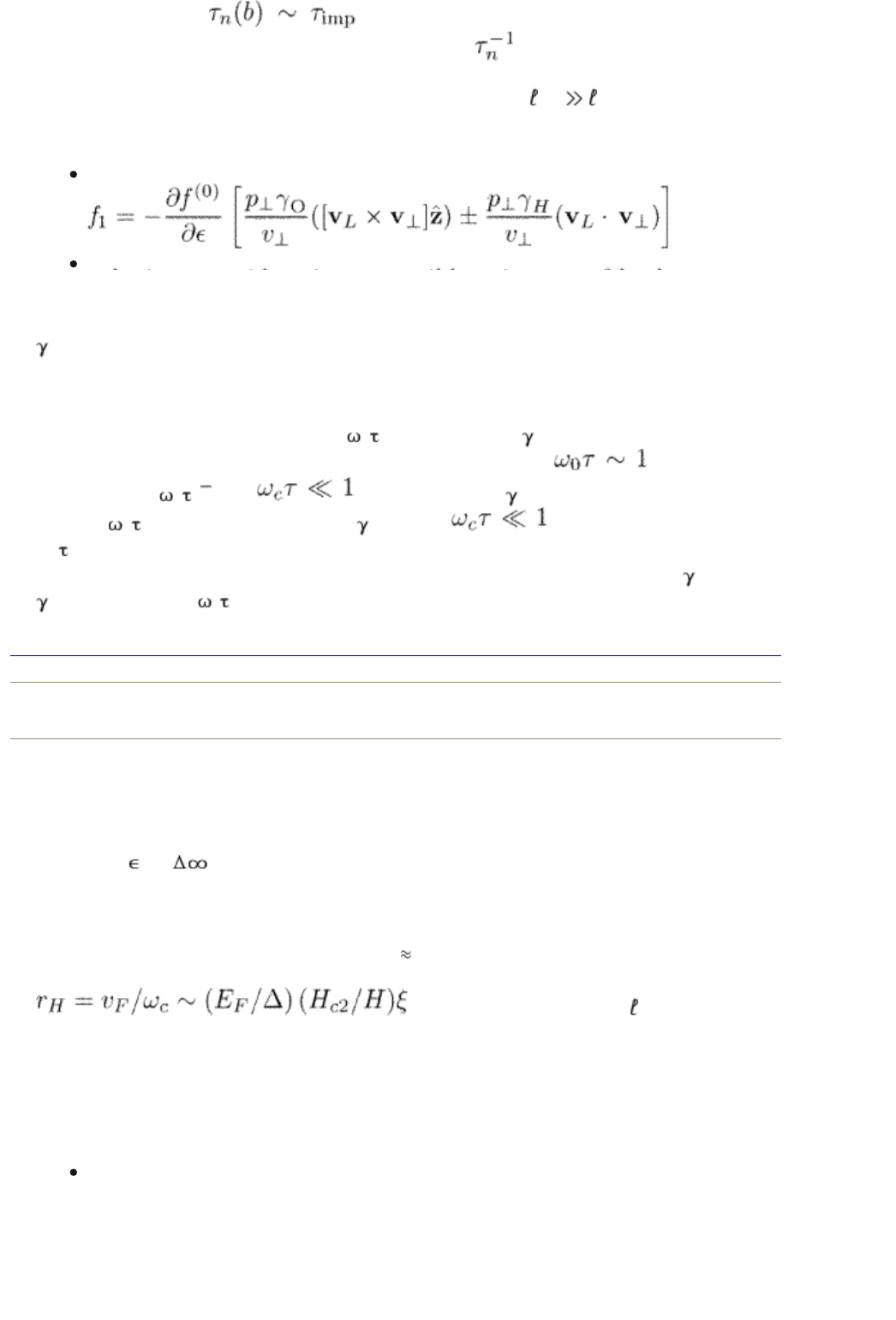
for all states where is the effective scattering time. Within the

relaxation-time approximation the relaxation rate

can also include electron–

phonon and electron–electron collisions. The electron–phonon scattering can be

important for very low concentration of Impurities when

imp

We also write the distribution function in a more general form

(14.51)

where we take into consideration a possible existence of both particle-like (the

upper sign) and hole-like (lower sign) carriers in the normal slate. The factors

O,H

arc found from eqn (14.42) with help of eqn (14.50). They are determined

by eqn (14.14) and coincide with the result obtained earlier within the

Boltzmann kinetic equation. Equation (14.14) reproduces reasonably well the

most important feature of the exact expression (14.48) and (14.49) for the

lowest level n = 0: As a function of

, the parameter

first increases

linearly, reaches the maximum value of the order unity for

and then

decreases as (

)

for . The parameter

grows monotonously

first as (

)

and then saturates at

= 1 for see Fig. 14.1. The use

-approximation allows us to find the distribution function for levels with

higher energies, as well. We see that the general trend of the parameters

o and

h as functions of

is the same as for the low-energy level.

end p.287

14.4.2 Delocalized excitations

One would expect that, if the density of moving vortices is small enough, the

deviation of the distribution function from equilibrium for the excitations with

energies |

|> should vanish at large distances, where the excitations are in

equilibrium with the crystal lattice or sample boundaries. However, for a finite

vortex density, when the distance between vortices is shorter than the magnetic

field penetration depth, one has to take into account also the motion of electrons

in the magnetic field with the induction B

H, where H is the applied field. Their

behavior is determined by the relation between the Larmor radius

and the mean, free path .

The trajectory of a delocalized quasiparticle crosses many vortex unit cells at

various distances from vortex axes, i.e., at different impact parameters. Since

the distribution function f

is constant along the trajectory it should thus be

independent of the impact parameter as well. Let us integrate eqn (14.35) over

the unit cell of the vortex lattice. Using eqn (14.38) we obtain

(14.52)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 16:09

The second line gives zero because the functions under the gradient do not

increase with distance; the average gradient should thus vanish. For example,

one can see that

where Q and are the gauge-invariant potentials eqns (1.46) and (1.75)

periodic in a vortex lattice. Using the identity eqn (14.34) we find

(14.53)

The integral of the last term is determined by large distances from the vortex

core where the Green functions g

–

and f

–

are determined by eqn (14.33),

Equation (10.74) results in the collision integral

Therefore,

Inserting this into eqn (14.53) we find the factors

O,H

in eqn. (14.51)

end p.288

(14.54)

where we replace

imp

with for brevity. The primes refer to the fact that these

expressions apply for |

| > The cyclotron frequency is

(14.55)

The modulus of charge appears due to our choice of the z-axis.

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 16:09

Comparing eqns (14.14) and (14.54) one concludes that localized particles in the

vortex core move like a charge in a magnetic field corresponding to the cyclotron

frequency

. By the order of magnitude, .

One can say that the behavior of localized excitations in the moving vortex is

similar to that of a charge in a magnetic field of the order of H

. This contrasts

to the Bardeen and Stephen (1965) assumption of the effective field being the

external field H.

For high fields,

we obtain for the distribution function in eqn (14.51)

(14.56)

This equation suggests the total distribution function in the form f = f

(0)

( –P ·

) showing that the excitations move together with the vortex. Indeed,

delocalized excitations cannot relax at the heat bath, since they cannot escape to

distances longer than r

, On the contrary, for low fields such that

and r

, we have f

( f

(0)

/ ). In this case the delocalized excitations

are almost in equilibrium with the heat bath and do not participate in the vortex

motion.

One can look at this from a slightly different point of view. Consider the mean

free path of delocalized excitations with respect to their collisions with vortices. If

the vortex cross section is

, the mean free path is = 1/ n

where n

is the density of vortices. We shall see later in Section 14.6.3 that the

vortex cross section is

[compare with eqn (14.100)] so that

(14.57)

i.e., ~ r

. In the limit , the vortex mean free path becomes

shorter than the impurity mean free path

imp

F imp

so that the delocalized

excitations scatter on vortices more frequently than on impurities and thus come

to equilibrium with moving vortices. A similar consideration also applies to

localized excitations: In the limit

interaction with a vortex is

more effective than relaxation on impurities, the excitations thus relax to

equilibrium with the moving vortex.

The case of low fields corresponds to electrically neutral superfluids, where r

. At the first glance, it is simply because

vanishes together with the charge

of carriers. However, this is not completely correct. In fact, to estimate a

deviation from equilibrium of delocalized excitations in this case one has again

end p.289

to compare the mean free path of excitations with their mean free path with

respect to scattering by vortices. Keeping in mind that the vortex density is n

/k where is an angular velocity of a rotating container and k = /m is the

circulation quantum, eqn (14.57) gives

/ . We observe that the cyclotron

frequency is replaced with the rotation velocity in a full compliance with the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 16:09

Larmor theorem. The ratio of the particle-particle mean free path to the vortex

mean free path is

. With the practical rotation velocity of a few

radians per second one always has

exceedingly larger than . Delocalized

excitations are thus at rest in the container frame.

Consider this in more detail. The kinetic equations (10.41) and (10.44) at large

distances from the vortex give

(14.58)

(14.59)

We keep the collision integral in the second equation because the distances

which we are interested in are of the order and larger than

, thus eqn (14.36) is

not sufficient, see page 198. The functions f

and f

are independent of the

distance along the trajectory for

. These constants are coupled to each

other by the conditions f

= g

–

for s + and f

= –g

–

for s which

follow from the fact that eqns (14.58), (14.59) should not have exponentially

increasing solutions. They are the boundary conditions to be imposed at distances

s larger than the core size of the vortex, but shorter than

. For delocalized

excitations with

above the gap at infinity, these boundary conditions give f

. As a result both f

and f

are small. Indeed, since f

~ f

one can neglect both

the term with

/ P and the collision integral in eqn (14.35) compared to the

term containing f

. The distribution functions f

and f

which come from eqn

(14.35) are then, by the order of magnitude, (

)( f

/ ). Hence the

distribution function f

for > is by the factor of

smaller than its magnitude for < and should be considered as zero. This

agrees with eqn (14.54) in the limit

14.5 Flux flow conductivity

The force from environment on a vortex is determined by the equation (13.10).

Remind that the nonequilibrium Green function is, according to eqn (13.15)

(14.60)

The main contribution to eqn (14.60) comes from the part containing f

. The

force from environment eqn (13.10) becomes

(14.61)

end p.290

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 16:09

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 16:09