Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

more detailed discussion because it has been a matter of controversy for a long

time since first calculated for vortices in helium II by Lifshitz and Pitaevskii

(1957) and then by Iordanskii (1964). Consider for simplicity a spherical Fermi

surface. The full transverse force from eqns (14.64) and (14.65) is

(14.88)

end p.298

In the superclean limit, when both

and

are much larger than unity, the

factors

H =

= 1, and the transverse force becomes (see page 276)

(14.89)

The balance eqn (14.7) against the Lorentz force gives the transport current in

the form

(14.90)

This equation is consistent with the Helmholtz theorem of conservation of

circulation, in an ideal fluid: vortices move together with the flow. On the

contrary, the transverse force disappears in the limit

. This is

the overall behavior of the transverse force as a function of the quasiparticle

mean free path.

From the historical point of view it is interesting to identify several contribution

to the transverse force and consider them one by one. We can present the full

transverse force in the form

(14.91)

where N

is the density of normal quasiparticles at large distances from the

vortex core

(14.92)

while superconduting density is N

= N – N

. The force

(14.93)

is called the spectral flow force (Kopnin et al. 1995).

Let us consider now the transport current that enters the force balance equation

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:10

through the Lorentz force. In presence of an electric field,

the transport current is not entirely due to a supercurrent, a part of it being

carried by delocalized quasiparticles. Far from the vortex core, the quasiparticle

(normal) current is

(14.94)

Using eqns (14.9) and (14.54) we find

(14.95)

Writing the transport current as j

= N

+ j

(qp)

we get the force balance eqn

(14.4) in the form

end p.299

(14.96)

Here

is the Magnus force;

(14.97)

is the Lorentz force from the quasiparticle current eqn (14.95). The force

is called the Iordanskii force (Iordanskii 1964). The Iordanskii force is the

counterpart of the Magnus force for normal excitations. We have included the

normal velocity v

to make this similarity more transparent. In our consideration,

the normal velocity is always zero v

= 0 since the equilibrium corresponds to

excitations at rest in the reference frame associated with the crystal lattice.

The spectral flow force F

is mostly due to the momentum flow from the Fermi

sea of normal excitations to the moving vortex via the gapless spectral branch

(the term n = 0 in the sum) going through the vortex core from negative to

positive energies (Volovik 1986, Stone and Gaitan 1987). Due to the

time-dependent angular momentum of the excitations

, there appears a flow (with the velocity

/ t) of spectral levels characterized by the angular momentum . Each particle

on a level carries a momentum p

. The momentum transfer to the vortex is

effective if the quasiparticle relaxation occurs quickly: the factor

in the first line of eqn (14.93) accounts for the relaxation on localized levels: the

relaxation and hence the momentum transfer is complete for

, and

vanishes in the opposite limit. The first term in eqn (14.93) thus describes a

disorder-mediated momentum flow along the anomalous chiral branch

( ) for

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:10

energies below the gap. The second line in eqn (14.93) accounts for the spectral

flow for energies above the gap. The corresponding factor which takes into

account the relaxation rate is

The spectral flow force vanishes in the limit

when both

and such that the transverse force is given by eqn (14.89). The

quasiparticle current is j(

) = N

so that the force from the quasiparticle

current compensates the Iordanskii force. The force balance eqn (14.96) reduces

to F

= 0. The vortex thus moves with the superfluid velocity v

= v

. As follows

from eqn (14.56), quasiparticles also have a velocity v

so that all the particles

move together which amounts to the total current as in eqn (14.90).

On the contrary, the spectral flow force has its maximum value for moderately

clean limit,

. Equation (14.93) gives in this limit

This completely compensates the first two terms in eqn (14.91), i.e, the

Iordanskii force and the part of the Magnus force that contains the vortex

velocity; the

end p.300

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:10

transverse force vanishes. The quasiparticle current vanishes even faster

because

. The Lorentz force is balanced only by a friction force F . As a

result, the dissipative dynamics is restored.

The low-field limit when

is most practical for superconductors.

Moreover, this regime is realized in electrically neutral superfluids such as

He.

As we already know, the low field limit

corresponds to a situation

when the delocalized excitations are at rest with the heat bath. Since delocalized

excitations are in equilibrium the quasiparticle current vanishes. The force

balance becomes

(14.98)

where the spectral flow force is

(14.99)

It is interesting to note that the spectral flow force from above gap states in this

case is related to the anomalous contribution to the transverse vortex cross

section for scattering of delocalized quasiparticles. The transverse vortex cross

section was calculated by Kopnin and Kravtsov (1976 b) and by Galperin and

Sonin (1976):

(14.100)

Inserting eqn (14.100) into the expression for the force exerted on the vortex by

scattered excitations,

(14.101)

we recover the last two terms in eqn (14.91) that are due to the normal

excitations, namely the term and the last term in the spectral

flow force eqn (14.99).

The first term in eqn (14.100) corresponds to the cross section of a vortex in a

Bose superfluid (Sonin 1987)

(14.102)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [301]-[305]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共5页 2010-8-8 16:11

where is the group velocity defined by eqn (1.88) which, in our case, is

, and m

is the mass of a Bosonic atom. Note that, in our

case. m

= 2m. The corresponding part of the transverse cross section can be

easily obtained from the semi-classical description. Indeed, the Doppler energy

due to

end p.301

the vortex velocity is P · v

= P · /m

. Its contribution to the quasiparticle

action is

Hero s =

t is the coordinate along the particle trajectory as in Fig. 6.1. and

is the variation of the order parameter phase along the trajectory. The change in

the transverse momentum of the particle is

p = A/ b hence the transverse

cross section becomes

where A

is the action along the trajectory passing on the left (right) side of the

vortex. Since

– x

–

= – 2 we recover eqn (14.102). With this expression

for the cross section, eqn (14.101) gives the Iordanskii force

The second term in eqn (14.100) originates from the fact that here, as distinct

from the situation in a Bose superfluid, the phase of the single-particle wave

function changes by

upon encircling the vortex, while it is the order parameter

phase which changes by 2

. It is this singularity, produced by the vortex in the

single-particle wave function, which results in the anomalous contribution to the

cross section in eqn (14.100). Inserted into eqn (14.101). it exactly reproduces

the second term in eqn (14.93) taken for

. We see that the spectral

flow force is related to a single-particle anomaly associated with the vortex.

end p.302

15 BOLIZMANN KINETIC EQUATION

Nikolai B. Kopnin

Abstract: This chapter derives the canonical Boltzmann kinetic equation for two

particular examples. First case is a superconductor with homogeneous in space

order-parameter magnitude and current. The second example treats the

excitations in the vortex core. The Boltzmann equation is then applied to

calculate the vortex momentum and vortex mass. It is also used for the vortex

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共5页 2010-8-8 16:11

dynamics in a d-wave superconductor. The non-trivial behaviour of the d-wave

flux-flow conductivity and the Hall effect is discussed.

Keywords: kinetic equation, vortex momentum, vortex mass, d-wave

superconductor, flux-flow conductivity, Hall effect

We derive the canonical Boltzmann kinetic equation for two particular

examples. First case is a superconductor with homogeneous in space

order-parameter magnitude and current. The second example treats the

excitations in the vortex core. The Boltzmann equation is applied to

calculate the vortex mass and to study the vortex dynamics in a d-wave

superconductor.

15.1 Canonical equations

The microscopic nonstationary theory of superconductivity based on the Green

function technique is a powerful method to describe the vortex dynamics both in

dirty and in clean superconductors, as well as in other superfluid Fermi systems.

However, a practical disadvantage of the method is its mathematical complexity,

which tends to hide the physical picture of the phenomenon. For a clean system,

where the excitation spectrum is well defined, an alternative way to deal with

dynamical processes is expected to be based on the quasiclassical Boltzmann

kinetic equation. For normal metals, the equivalence of the quasiclassical Green

function approach to the Boltzmann equation has been demonstrated by Keldysh

(1964). In Chapter 10 we have derived the set of kinetic equations which are

suitable for many nonstationary problems in the theory of superconductivity. In

the present chapter we consider a few examples for which the generalized kinetic

equations can be reduced to the canonical Boltzmann form

(15.1)

Where ( f/ t)

coll

is the collision integral and

(q, p) is the quasiclassical

excitation spectrum, characterized by the canonically conjugated generalized

“coordinate” q and. “momentum” p of the excitation (n denotes the set of other

quantum numbers). The first example is the case of constant in space order

parameter and supercurrent. We shall see that the Boltzmann equation is in this

case completely similar to its normal-metal counterpart. Other examples refer to

the dynamics of excitations in the presence of moving vortices.

15.2 Uniform order parameter

One can easily derive the canonical form of the Boltzmann equation for a

situation where the order parameter magnitude, supercurrent, and external

fields only

end p.303

slowly vary in space and in time (Betbeder-Matibet and Nozières 1969, Aronov et

al. 1981, 1986). We have already discussed this equation in Section 1.2.3. Let us

define the energy of excitations as in eqn (1.54)

(15.2)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共5页 2010-8-8 16:11

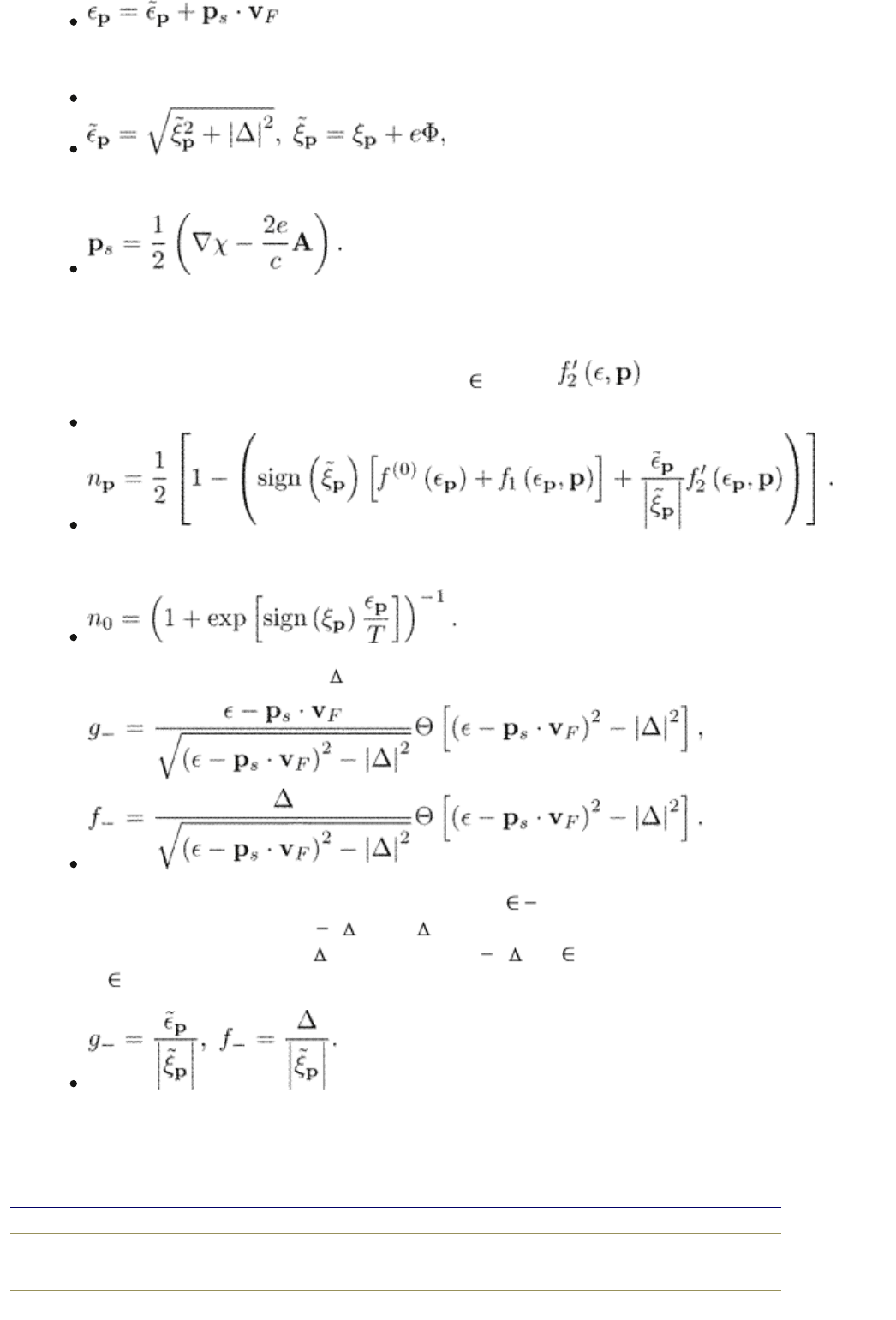
where

(15.3)

and

According to the definition eqn (15.2), the excitation energy is always positive.

This coincides with the Landau picture of the Fermi liquid. We define the

distribution function for the excitations with the energy spectrum eqn (15.2)

through our generalized distribution functions f

( , p) and as

(15.4)

In equilibrium, it is the Fermi function

We also note that for a constant | | and p

, the Green functions are

The radicals are defined as analytical functions of x = p

· v

on the complex

plane of x with the cut between

| | and | | (see Fig. 5.1); they change sign

when x goes from positive x > |

| to negative x < | |. If is replaced with a

positive

, the Green functions become

One can check after some algebra that in the linear approximation with respect

to the deviation from equilibrium, the two equations (10.52) and (10.53)

end p.304

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共5页 2010-8-8 16:11

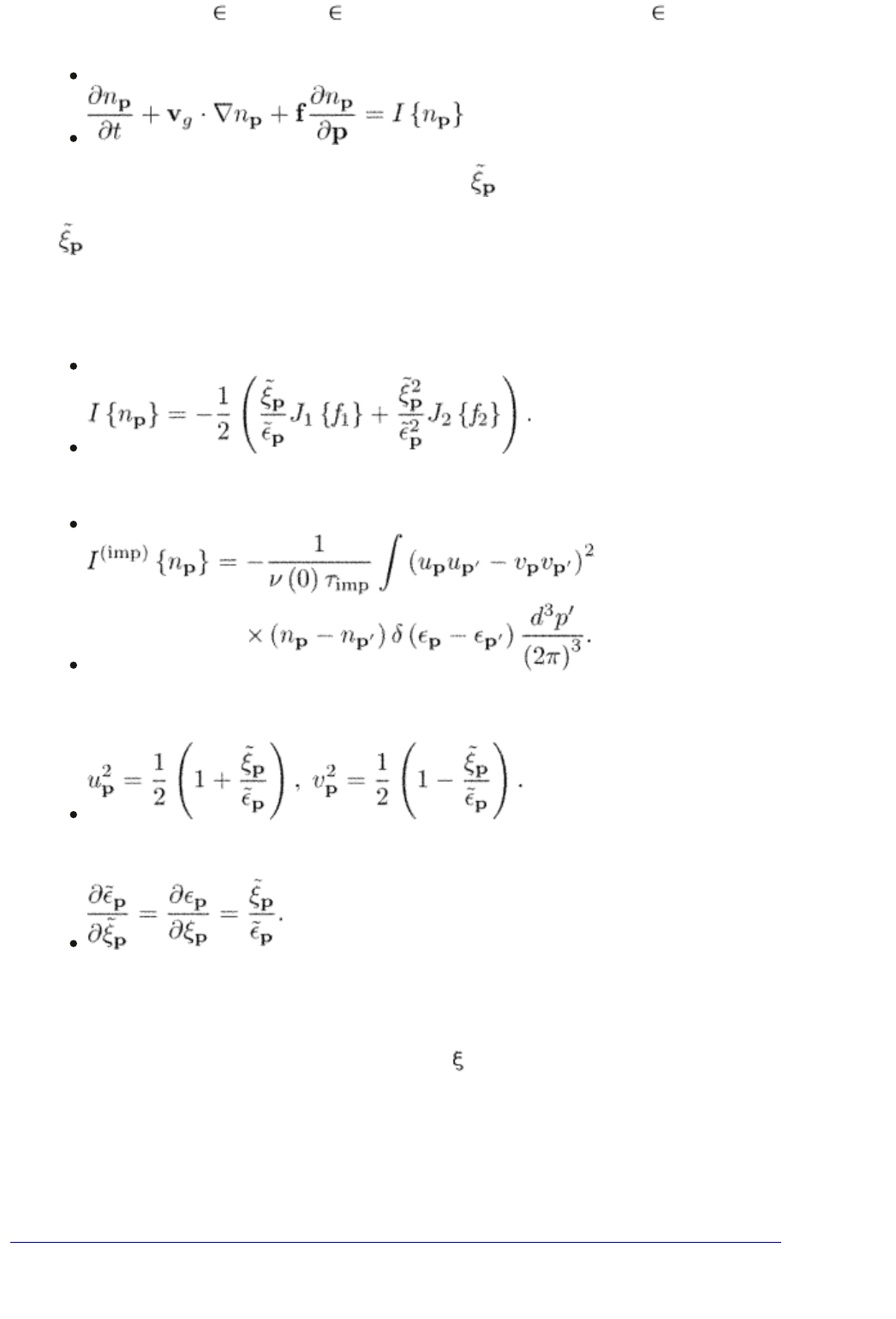
for the functions f

( , p) and f

( , p) possessing a definite parity in ( , p) can

be written as one equation

(15.5)

for the function n

which has no definite parity in . Equations (10.52) and

(10.53) can be recovered from eqn (15.5) by separating the even and odd parts

. The group velocity v

and the elementary force f including the Lorentz

force are defined in eqn (1.88). Equation (15.5) coincides with eqn (1.87) used in

the beginning of this book.

The collision integral in eqn (15.5) has the form

(15.6)

For example, the impurity collision integral becomes

(15.7)

The Bogoliubov–de Gennes coherence factors are as in eqn (1.56)

During the transformation we use the relation

Equation (15.5) has the form of the canonical Boltzmann equation. However, its

region of applicability is limited to the situation where the order parameter and

the supercurrent are almost uniform in space. One would think that the required

scale of spatial variations should be larger than

. However, this condition does

not guarantee that the obtained results are correct. The point is that the spatial

variations also result in distortions of the quasiparticle spectrum. These

distortions are not included into eqns (15.2), (15.3) though they can be

important for some of the responses. We consider now one such example when

the distortion of the spectrum provided by eqns (14.31) and (14.32) is important

for calculating the flux flow conductivity.

end p.305

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共5页 2010-8-8 16:11

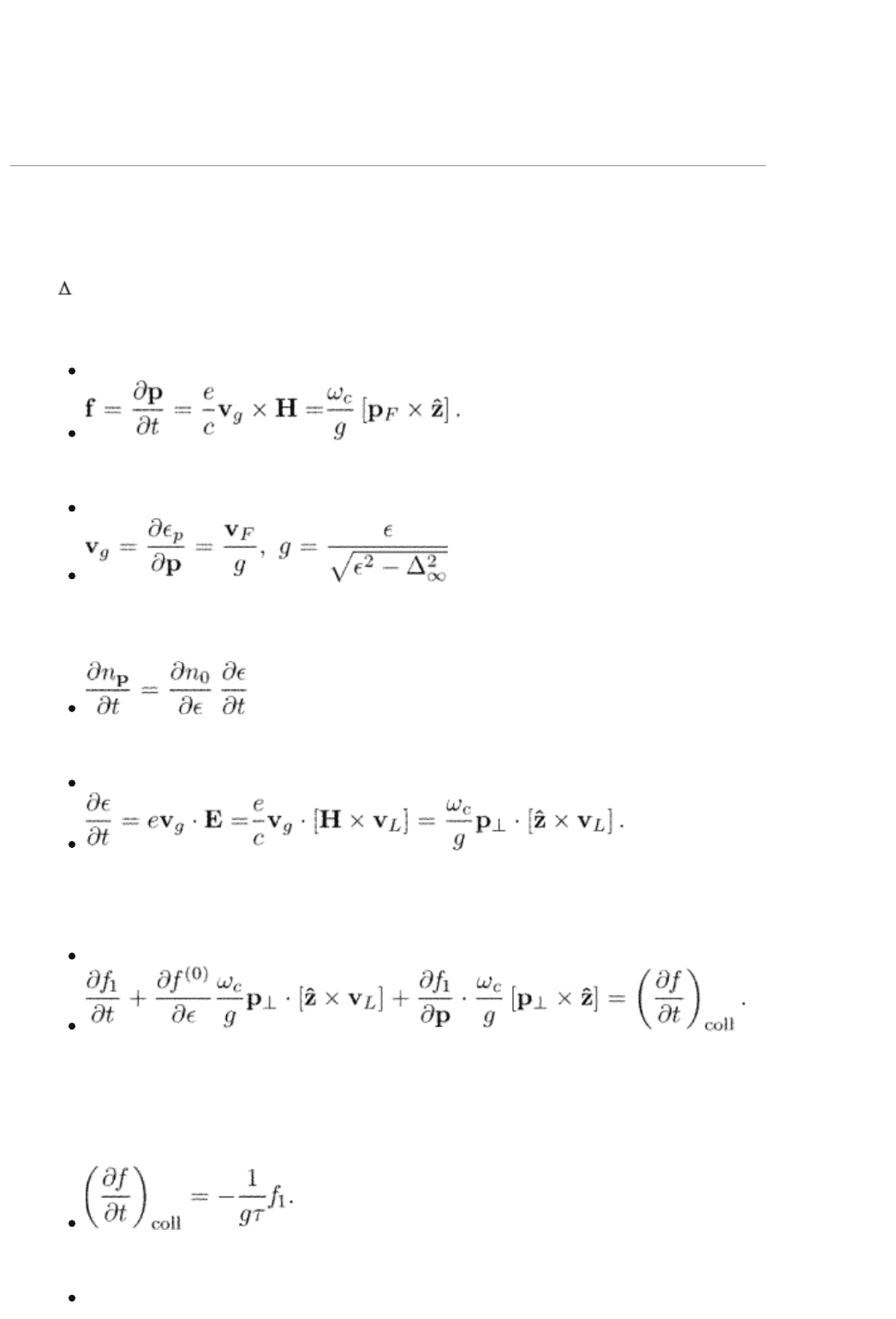
15.2.1 Boltzmann equation in presence of vortices

A delocalized particle moves mostly far from the vortex core where the order

parameter is constant and the superfluid velocity potential pv

is small compared

. One could thus expect that the kinetic equation for delocalized excitations

has its conventional form eqn (15.5) derived above. However, this is not exactly

the case. To see this let us put the elementary Lorentz force in eqn (15.5) to be

(15.8)

This expression contains the group velocity

(15.9)

in contrast to the previous definition eqn (1.88) that simply has v

. The driving

term is also written in a slightly different way. We put

where the time-derivative of energy

(15.10)

now also contains the group velocity instead of v

as in eqn (1.90).

The kinetic equation for the function f

becomes

(15.11)

The spatial derivative of the distribution function vanishes since f

is constant in

space.

For the energy spectrum of eqns (15.2, 15.3) the collision integral eqn (15.6)

reduces to

Finally, the kinetic equation (15.11) for a steady distribution takes the form

(15.12)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [306]-[310]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:11

which coincides with the microscopic equation (14.53). Its solution provides the

distribution function in the form of eqn (14.51) with the factors

determined

by eqn (14.54).

end p.306

It is thus eqn (15.11) that should be used for quasiparticles traveling through the

vortex array rather than eqn (15.5) derived assuming a constant order

parameter and uniform supercurrents. The correct equation contains the group

velocity rather than v

in the elementary force eqn (15.9) and in the energy gain

eqn (15.10). Looking back at the derivation of eqn (14.53) we observe that if we

had omitted the gradient terms from

in eqn (14.52) we would only have

(e/c)[v

× H]g left in [see eqn (13.11)] and would thus obtain an extra

factor g

both in eqn (15.10) and in front of the elementary Lorentz force. The

compensating contribution comes from the gradient expansion eqns (14.31,

14.32) through the identity eqn (14.34).

15.3 Quasiparticles in the vortex core

Consider another example of application of the Boltzmann equation to the vortex

dynamics in clean superconductors. We study kinetic of excitations localized in

the vortex cores (Stone 1996, Kopnin and Volovik 1997). We start with an

observation that eqn (14.42) which we derived from kinetic equations (14.35)

and (14.36) already looks almost like the canonical equation (15.1). In this

section we present a microscopic verification of (15.1) for a genera case (Blatter

et al. 1999) when

can depend on the quasiparticle momentum as it is the case,

for example, in d-wave superconductors. We demonstrate that our kinetic

equations for the generalized distribution function derived from the quasiclassical

Green function formalism can be further transformed into the simple and

physically transparent canonical equation (15.1). We restrict ourselves to the

particular example of vortex dynamics; the calculation can be generalized to

include the dynamics of other topological defects in superfluid Fermi systems.

In Section 14.5, we have derived microscopically the force acting on a moving

vortex, eqn (14.62). This equation shows that, within the quasiclassical

approximation, the force F

env

can be represented as the momentum transfer from

the heat bath via the localized quasiparticle excitations to the vortex [compare

with equ (14.4)],

(15.13)

where p

/ t =

(q, p)/ q and d is the dimensionality of the problem (d = 1

in case of vortices). Our analysis thus provides a microscopic verification of the

phenomenological approach to the vortex dynamics based on the concept of

semiclassical particles obeying the Boltzmann kinetic equation where the

quasiclassical spectrum

of excitations in the vortex core plays the role of the

Hamiltonian, and the force acting on the vortex results from the elementary

force

/ t the quasiparticles exert on the vortex core. Later in this chapter, we

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 16:11