Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

consider two more examples of implementation of this scheme. In Section 15.4

we calculate the vortex mass. Another example is the vortex dynamics in d-wave

superconductors to be discussed in Section 15.5.

end p.307

15.3.1 Transformation into the Boltzmann equation

Let us write the kinetic equations (10.41) and (10.56) again. We have

(15.14)

and

(15.15)

We start with a few preparatory steps before transforming the kinetic equation

(15.14) into the Boltzmann equation. We again use the coordinate frame

associated with the vortex as shown in Fig. 6.1. Recall that the z-axis is chosen

parallel to the axis of the vortex, with the positive direction along the vortex

circulation

. The distance along the quasiparticle trajectory as

well as the impact parameter are s =

cos( ) and b = sin( ),

respectively, where

and are the radial distance and the azimuthal angle in

the cylindrical frame, and

is the angle between v and the x-axis. In this

representation, the quasiclassical Green function is specified by the momentum

projection on the vortex axis

, the momentum direction in the

plane perpendicular to the vortex axis, and the impact parameter b, which is

related to the angular momentum µ = bp

, with p the momentum projection

on the plane perpendicular to the vortex axis. For simplicity, we consider a

spherical Fermi surface here. Up to corrections of order (p

)

we can assume

straight quasiparticle trajectories and thus the angular momentum µ is a

conserved quantity even for a non-axisymmetric vortex.

Next, we transform the operators in eqn (15.14). The momentum derivative

in eqn (15.14) is taken at a constant position vector r = (

, ) with respect to

variations in the momentum direction, with the magnitude of the momentum

being fixed at the Fermi surface. The planar projection can be written as

with the unit vector in the direction of v . Changing to variables s and b,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 16:11

the derivative with rospect to becomes

and the spatial gradient in the (s, b) frame is

(15.16)

end p.308

In the presence of a vortex, the order parameter has the form

( , ) =

(a, s, b)e

. Here

( , s, b) is the order parameter expressed in the

coordinate frame (s, b), where the azimuthal angle is measured from the

momentum direction. For a non-axisymmetric vortex and/or in a d-wave

superconductor,

(a, s, b) can have an explicit dependence on the angular

coordinate

To work with various terms in the kinetic equation (15.14) we use

transformations very similar to those we made in Section 14.2 to derive

identities for the quasiclassical Green functions. Keeping in mind that f

independent of s (see eqn (15.15)), we rewrite the terms in the second and third

lines of eqn (15.14) in the form

(15.17)

and

(15.18)

Moreover, since A floes not depend on the momentum direction, we can subtract

the zero term

from the third line of eqn (15.14). Next, we integrate (15.14) along the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:11

quasiclassical trajectory, using f

/ s = 0 and one of the Eilenberger equations,

(15.19)

After some algebra the second and third lines in the l.h.s. of eqn (15.14) take the

form

(15.20)

The term A

/ accounts for the explicit -dependence picked up by the vector

potential when expressed in the coordinate frame (s, b). The s-derivatives

present

end p.309

in eqns (15.17) and (15.18) disappear in eqn (15.20), as can be seen from the

identity (14.29). In particular, taking the v

projection of eqn (14.29) we find,

It is this relation which serves to eliminate the s-derivatives from eqn (15.20).

The first term in the r.h.s. of eqn (15.20) has the form

which can also be transformed with the help of eqn (14.29). The second term has

the form

It can be transformed using the relation

(15.21)

which can easily be derived in exactly the same way as eqn. (14.29). As a result,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:11

the r.h.s. of eqn (15.20) takes the simple form

(15.22)

Next, we concentrate on the first line of eqn (15.14). The driving term f

(0)

is the source of the nonequilibrium state as produced by time variations of the

order parameter together with the electric field. According to eqn (14.38), the

first term of the kinetic equation (15.14) can be written in the form

which then can be further transformed using eqn (14.29). The second term in the

first line of eqn (15.14) vanishes after integration over ds. The next term can be

transformed with help of the identity (14.25). We finally obtain

(15.23)

A similar equation (14.42) has been already derived in Section 14.4 for s-wave

superconductors. Note that the term with

/ b is absent in eqn (14.42) because

/ = 0 for an axisymmetric vortex in an s-wave superconductor.

end p.310

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:11

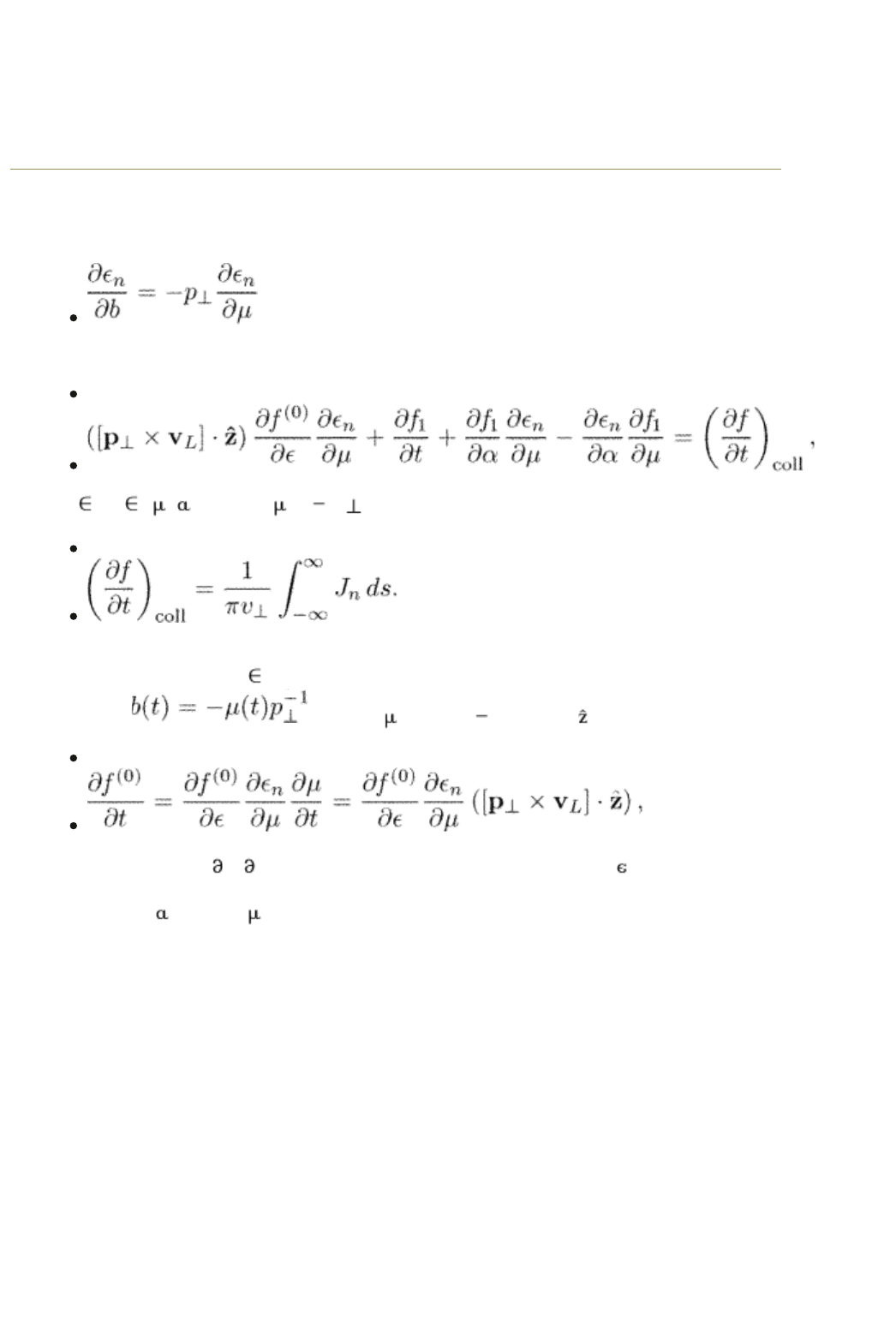
Equation (15.23) is nothing but the Boltzmann equation (14.3) used in the

beginning of this chapter. Indeed, consider various terms in eqn (15.23) and

compare them with eqn (14.3). Since

we have from eqn (15.23)

(15.24)

with

( , ; p

) and = bp . We denoted the collision integral as

(15.25)

The time-derivative term in eqn (14.3) is obtained from eqn (15.24) if we

assume that the energy

contains a time dependence through the impact

parameter

, where (t) = [(r v

t) × p] :

(15.26)

and combine it with f

/ t in the total distribution function f = f

(0)

(

) + f

Equation (14.3) can be rewritten into the generic form (15.1) with the canonical

variables q =

and p = .

To summarize the results of this section, we have started with the exact

microscopic description of the nonstationary processes in terms of the Green

function technique. Using the quasiclassical approximation, we have been able to

reduce the problem of finding the nonequilibrium state of the superconductor

with a moving vortex to the problem of solving the canonical Boltzmann equation

for the distribution of nonequilibrium excitations localized in the vortex core. The

only information needed to find the distribution function is the energy spectrum

of the equilibrium excitations in the vortex core. The knowledge of the energy

spectrum is also sufficient to calculate the force acting on the moving vortex. The

full problem of the vortex dynamics thus reduces to several much easier and

more transparent steps which are: finding the equilibrium energy spectrum of

the excitations in the vortex core, solving the Boltzmann equation, and, finally,

calculating the momentum transfer from the localized excitations.

15.4 Vortex mass

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [311]-[315]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:12

The vortex mass in superfluids and superconductors has been a long-standing

problem in vortex physics and remains to be an issue of controversies. There are

different approaches to its definition. In early works on this subject, the vortex

mass was determined through an increase in the free energy of a superconductor

end p.311

calculated as an expansion of retarded and advanced Green functions up to the

second order terms in slow time-derivatives of the order parameter. The

quasiparticle distribution was assumed to be essentially in equilibrium. First used

by Suhl (1965) (see also Duan and Leggett 1992) this approach yields the mass

of the order of one quasipaticle mass (electron, in the case of a superconductor)

per atomic layer. Another approach consists in calculating the energy E

/8 of

electric field which is proportional to the square of the vortex velocity. This gives

rise to the so-called electromagnetic mass (Coffey and Hao 1991) which, in good

metals, is of the same order of magnitude (see Sonin et al. 1998 for a review).

A serious disadvantage of the above definitions of the vortex mass is that they do

not take into account the kinetics of excitations disturbed by a moving vortex.

We shall see that the inertia of excitations contributes much more to the vortex

mass than what the old calculations predict. The kinetic equation approach

described here is able to incorporate this effect. To implement this method we

find the force necessary to support an unsteady vortex motion. Identifying then

the contribution to the force proportional to the vortex acceleration, one defines

the vortex mass as a coefficient of proportionality. This method was first applied

for vortices in superclean superconductors by Kopnin (1978) and then was used

by other authors (see for example, Kopnin and Salomaa 1991, Šimánek 1995).

The resulting mass is of the order of the total mass of all electrons within the

area occupied by the vortex. We will refer to this mass as to the dynamic mass.

The dynamic mass originates from the inertia of excitations and can also be

calculated as the momentum carried by localized excitations (Volovik 1997).

In the present section we describe how one can apply our kinetic equation

approach for calculating the dynamic vortex mass in a general case of a finite

relaxation time of nonequilibrium excitations produced by the moving vortex.

Following Kopnin and Vinokur (1998) we use the Boltzmann kinetic equation to

derive the equation for the vortex dynamics which contains the inertia term

together with all the forces acting on a moving vortex. We shall see that dynamic

mass displays a nontrivial feature: it is a tensor whose components depend on

the quasiparticle mean free time. In s-wave superconductors, this tensor is

diagonal in the superclean limit. The diagonal mass decreases rapidly as a

function of the mean free time, and the off-diagonal components dominate in the

moderately clean regime. Our results agree with the previous work (Kopnin

1978, Kopnin and Salomaa 1991, Volovik 1997) in the limit

15.4.1 Equation of vortex dynamics

To introduce the vortex momentum we consider a non-steady motion of a vortex

with a small acceleration. We start with localized excitations. Multiplying eqn

(15.24) by p

/2 and summing up over all the quantum numbers, we obtain

(15.27)

where the l.h.s. of eqn (15.27) is the force from the environment on a moving

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 16:12

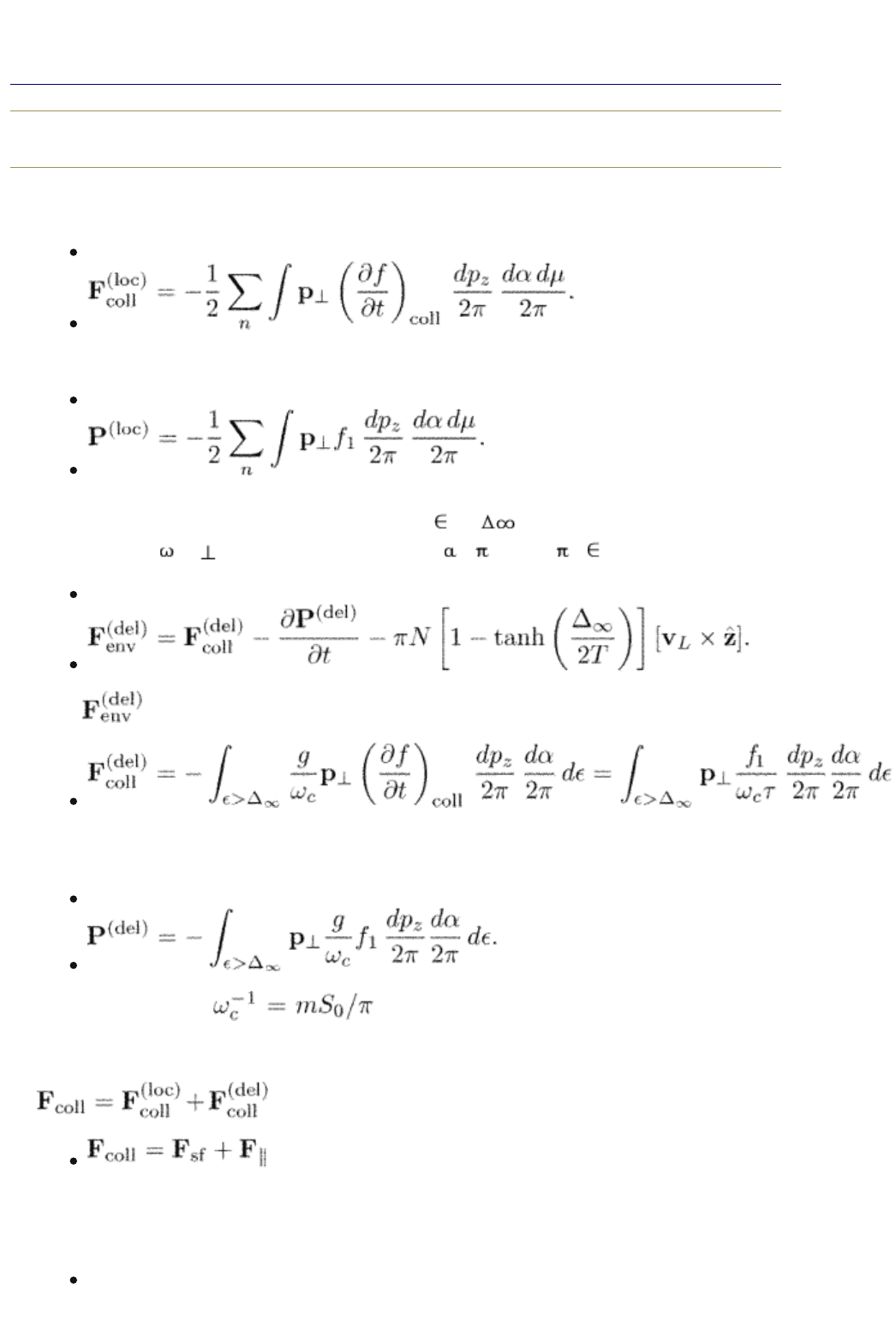
vortex eqn (14.4) derived in Section 14.5. The first term in the r.h.s. of eqn

(15.27)

end p.312

is the force exerted on the vortex by the heat bath via excitations localized in the

vortex core:

(15.28)

The second term in the r.h.s. of (15.27) is the change in the vortex momentum

(15.29)

To find the contribution from the states with | | > we multiplying eqn

(15.11) by (g/

)p /2 and integrate it over (d /2 ) (dp

/2 )d . We obtain

(15.30)

Here is determined by eqn (14.65),

is the force from the heat bath, while the corresponding contribution to the

vortex momentum is

(15.31)

Note that the factor is proportional to the particle mass and to

the area occupied by each vortex. The total momentum is P = P

(loc)

+ P

(del)

After a little algebra, the total force from the heat bath

can be written in the form

where the friction and spectral flow forces are determined by eqns (14.87) and

(14.93), respectively. The total force from environment eqns (15.27) and (15.30)

takes the form

(15.32)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 16:12

This equation agrees with eqn (14.91) for a steady motion of vortices.

The equation of vortex dynamics is obtained by variation of the superconducting

free energy plus the external field energy with respect to the vortex

displacement. The variation of the superfluid free energy gives the force from the

environment, F

env

, while the variation of the external field energy produces the

external Lorentz force. In the absence of pinning the total energy is

translationally invariant. Therefore, the requirement, of zero variation of the free

energy again gives the condition F

+ F

env

= 0 in the form of the force balance.

Using

end p.313

our expression for F

env

the force balance can now be written in the form similar

to eqn (14.96)

(15.33)

where the r.h.s. contains the time-derivative of the vortex momentum due to a

non-steady vortex motion. For a steady vortex motion, eqn (15.33) reduces to

eqn (14.99). The physical meaning of the eqn (15.33) is simple. The l.h.s. of this

equation accounts for all the forces acting on a moving straight vortex line. The

r.h.s. of eqn (15.33) comes from the inertia of excitations and is identified as the

change in the vortex momentum. This definition of momentum is similar to that

used by Stone (1996) and by Volovik (1997).

15.4.2 Vortex momentum

Having defined the vortex momentum, we calculate the vortex mass. The

distribution function is given by eqn (14.9). The vortex momentum becomes P

; it has both longitudinal and transverse components with respect to the

vortex velocity. For a vortex with the symmetry not less than the four-fold, the

effective mass tensor per unit length is M

= M

|| ik

M e

ikj j

where M

= M

||e

||h

, and M = M

= M

. Each component contains contributions from

localized and delocalized states such that

where

(15.34)

and

(15.35)

The same expression holds for M

e,h

where

is replaced with

. The e, h

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:12

subscripts indicate the corresponding momentum integrations over the electron

and hole parts of the Fermi surface, respectively.

If the vortex acceleration is slow, one can use expressions (14.14), (14.54) for a

steadily moving vortex to calculate the vortex inertia. Consider first the

contribution of the states with |

| > . Since do not depend on energy

and momentum, eqn (15.35) gives

Here N

is the density of normal particles (or holes). The contribution of the

delocalized states decreases as

gets smaller. In the limit of vanishing

the vortex mass is determined by localized excitations. The localized excitations

dominate also at low temperatures T

. One has in this case

end p.314

For 1 the mass tensor for delocalized states is diagonal M

= M

|| ik

where ; it is equal to the mass of all normal particles in the

area occupied by the vortex. The mass tensor for localized states becomes

diagonal in the superclean limit where

with

. This is the mass of all electrons in the

area occupied by the vortex core. The mass decreases with

. In the moderately

clean regime

where , the diagonal component

vanishes as

, and the mass tensor is dominated by the off-diagonal part.

We should emphasize an important point that, in contrast to a conventional

physical body, the mass of a vortex is not a constant quantity for a given system:

it may depend on the frequency

of the external drive. Indeed, for a nonzero

we find from eqn (15.24)

As a result, all the dynamic characteristics of vortices including the conductivity

and the effective mass acquire a frequency dispersion. In the limit

poles in

O,H

appear at a frequency equal to the energy spacing between the

quasiparticle states in the vortex core which gives rise to resonances in

absorption of an external electromagnetic field (Kopnin 1978, 1998 b).

15.5 Vortex dynamics in d-wave superconductors

In this section we consider the vortex dynamics in d-wave superconductors at low

temperatures. We specify later which temperatures can he considered as low. In

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:12

d-wave superconductors, the vortex dynamics is expected to be more intricate

due to a peculiar structure of the vortex-core stales. The presence of gap nodes

introduces the most import ant difference in the structure of core states

compared to an s-wave superconductor. As was shown in Section 6.4, instead of

a well-defined quasiclassical Caroli–de Gennes–Matricon interlevel spacing

the true quantum states in d-wave superconductors have a much smaller

separation

between quantum levels, , which depends

on the magnetic field. As a result, there appears another parameter

which

influences the vortex dynamics. We shall see that a new regime can he reached

in superclean superconductors with longitudinal and transverse components of

the conductivity tensor independent of the quasiparticle mean free time (Kopnin

and Volovik 1997, Kopnin 1998 b). It is realized when the relaxation rate is

smaller than the average distance between the quasiclassical energy levels

but larger than the separation between the true quantum-

mechanical states

15.5.1 Distribution function

Here we employ the Boltzmann kinetic equation derived earlier in this chapter.

We also use the spectrum of excitations in the vortex core calculated in Section

6.4. In d-wave superconductors, the gap at large distances from the vortex has

the form

|sin(2

)|. A particle is classically localized within the vortex core

end p.315

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:12