Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

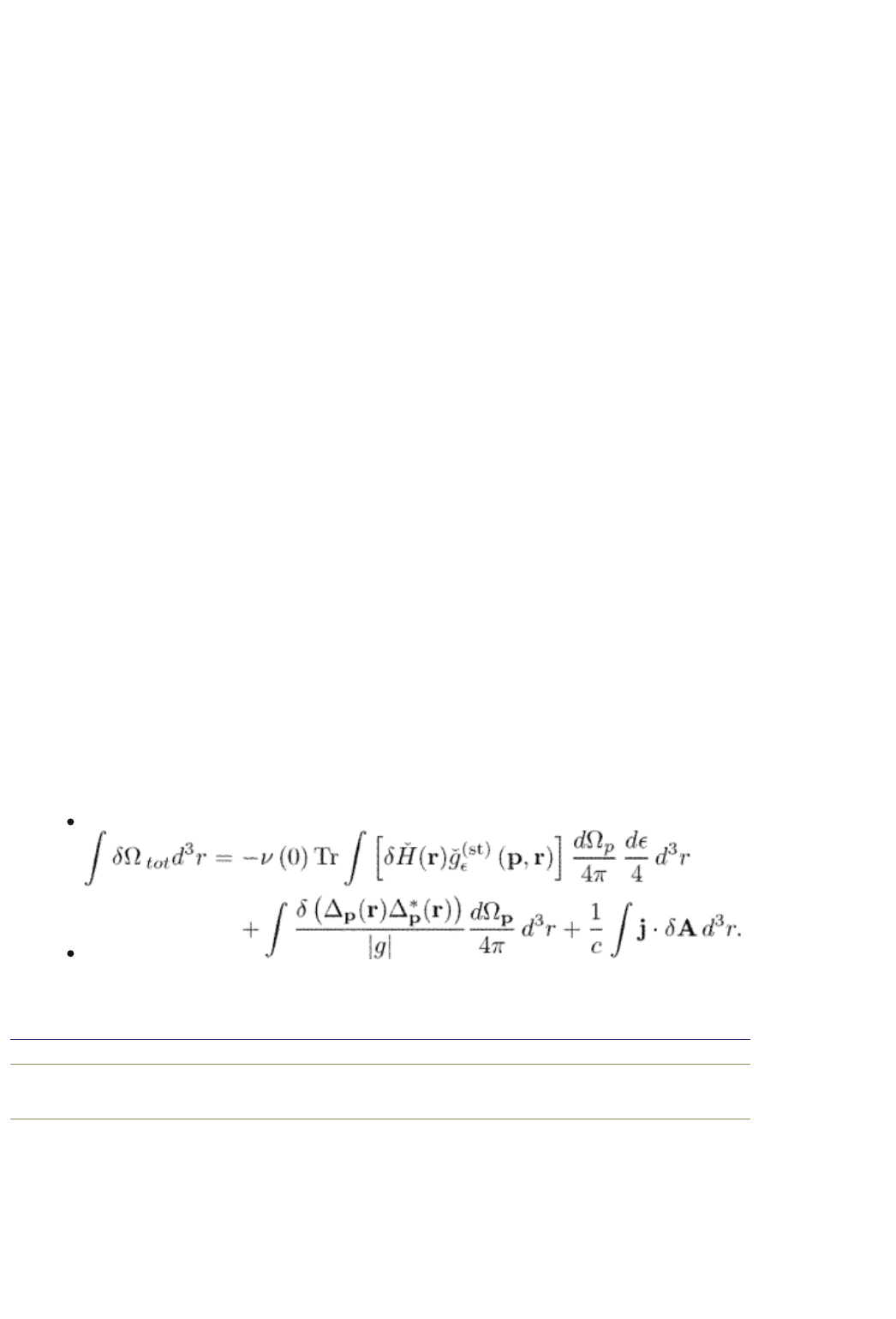
what is predicted by the conventional TDGL model. The flux-flow conductivity is

discussed as a function of temperature and the kinetic parameters.

Keywords: dirty superconductor, force, vortex, environment, Green

function, kinetic equation, flux-flow conductivity

The force exerted on a vortex from the environment is derived

microscopically. The kinetic equation is solved for the distribution function

of excitations driven out of equilibrium by the moving vortex; the flux flow

conductivity in a dirty superconductor is calculated. The vortex viscosity

appears to be much larger than what is predicted by the TDGL model.

13.1. Microscopic derivation of the force on moving vortices

The TDGL scheme can only be applied in very special situations under rather

restricting conditions of gapless superconductivity. This chapter treats the vortex

dynamics in a more general case when nonstationary processes in a

superconductor go beyond the TDGL model. We shall see that kinetics of

nonequilibrium excitations makes the nonstationary behavior of a superconductor

more complicated and diverse.

The complexity of the problem gives rise to the expectation that it would not be

easy to calculate anything beyond the simple TDGL equations. Fortunately, this is

not exactly the case, especially when we are interested in a linear response of a

vortex array to applied perturbations. The major simplification is that the force

on the moving vortex can be expressed through the characteristics of a static

vortex and through the solutions to the kinetic equations which only contain the

order parameter and magnetic field for a steady vortex array. The force thus

does not contain distortions of the order parameter and of the magnetic field

caused by the moving vortex. Restricting ourselves to the linear approximation in

the vortex velocity we start with the derivation of the general expression for the

force which acts on a moving vortex from the environment.

13.1.1 Variation of the thermodynamic potential

Let us consider a variation of the thermodynamic potential eqn (3.71) derived in

Section 3.3. We have in the real frequency representation

(13.1)

Here

end p.259

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:04

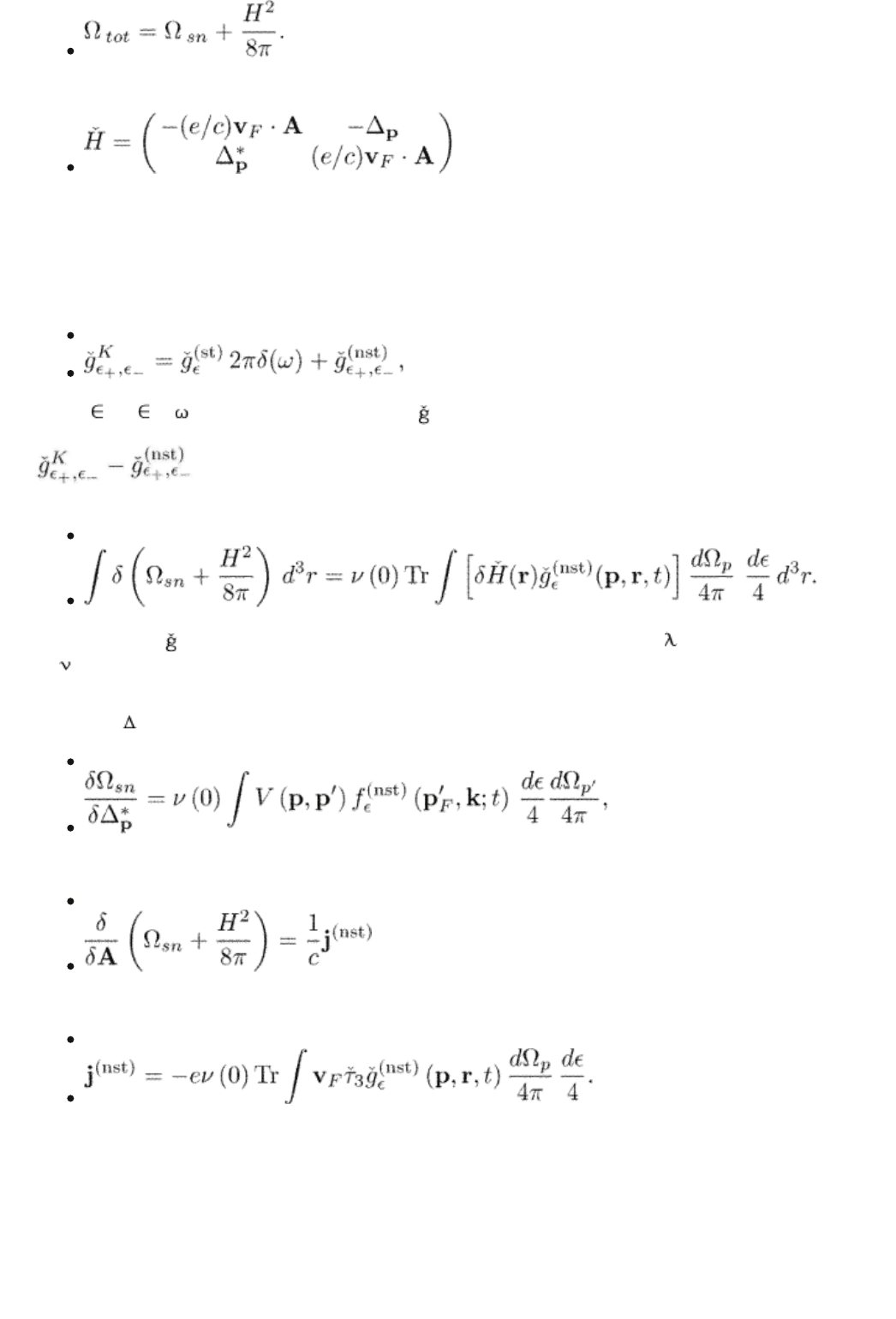
The Hamiltonian is

in the quasiclassical approximation. The variation eqn (13.1) is taken at a

constant chemical potential.

When the system is in a nonstationary state, the concept of thermodynamic

potential can be used only if deviations from the equilibrium are small. The total

Green function describing the nonstationary state in frequency representation is

(13.2)

where

= ± /2. It is the stationary part

(st)

which enters the variation of

the thermodynamic potential in eqn (13.1). We substitute it with the difference

, and take into account that the order parameter and the

current in the nonstationary state satisfy equations (9.17) and (9.18). We obtain

(13.3)

The terms with

disappear due to eqns (9.17) and (9.18) (we recall that =

|g| (0)).

Equation (13.3) determines the variation of the thermodynamic potential with

respect to and A. For example,

(13.4)

and

(13.5)

where

(13.6)

Equations (13.4) and (13.5) are microscopic counterparts of the corresponding

TDGL equations. The right-hand sides of these equations are proportional to

deviations from equilibrium; they vanish in a stationary state.

13.1.2 Force on vortices

Consider a variation of the total thermodynamic potential in the form

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:04

(13.7)

end p.260

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:04

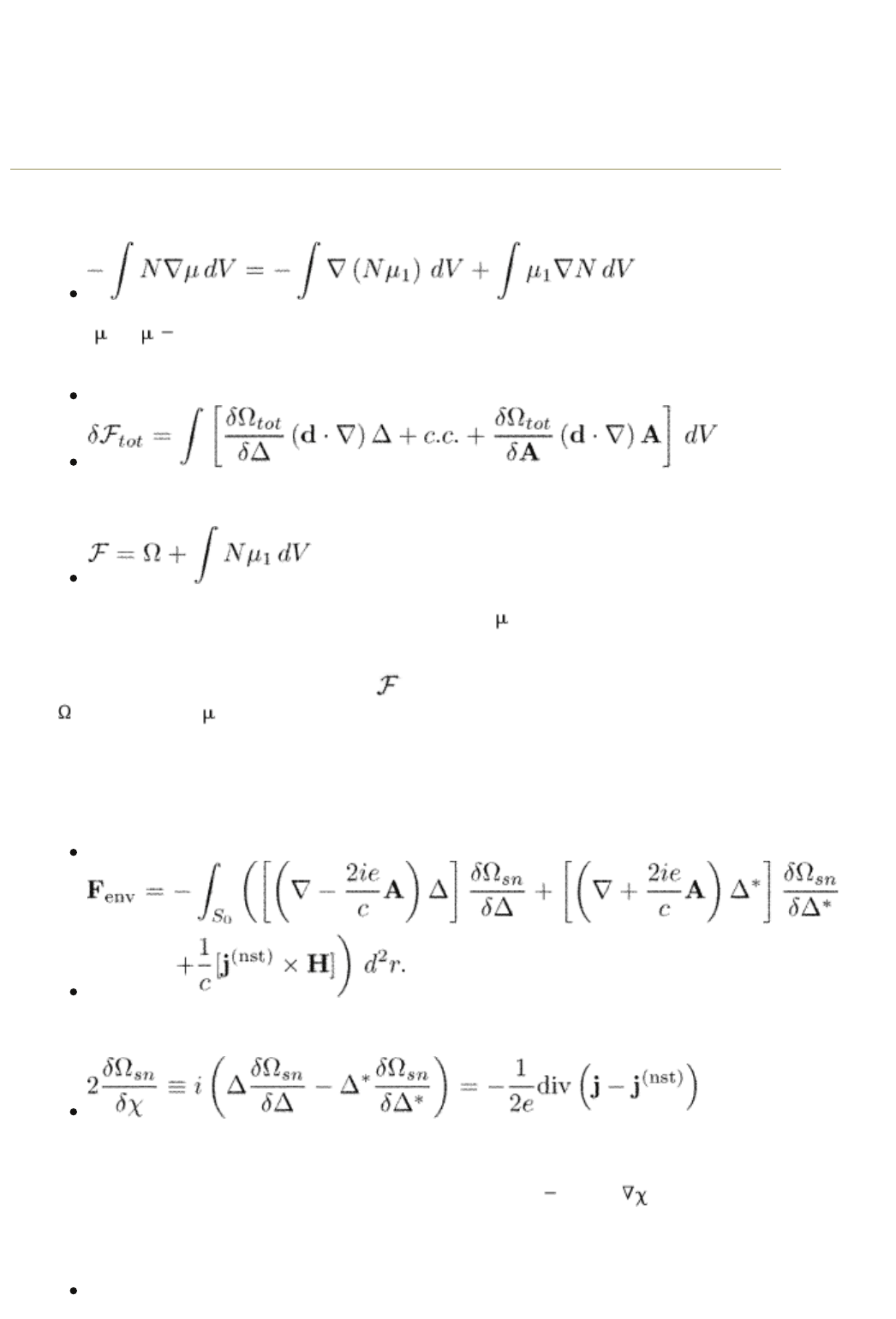
where d is an arbitrary constant vector of an infinitesimal translation. The last

term can be written as

where

= E

is the deviation of the chemical potential from its value in the

normal state. Equation (13.7) takes the form

(13.8)

where

is the free energy which is a function of N instead of . The gradient of the

particle density is omitted because the density is constant due to the charge

neutrality. Equation (13.8) follows from the general property of thermodynamic

functions: Variation of the free energy

for constant N is equal to the variation

for a constant . The gradient of free energy density for a constant number

of particles gives the density of force acting on the vortex from environment.

The r.h.s. of eqn (13.8) can be transformed in exactly the same way as we did it

earlier for the derivation of the force balance within the TDGL model in Section

12.4. The force from environment per unit vortex length becomes

(13.9)

The relation

used during the derivation follows from eqn (13.5) and the requirement of the

gauge invariance according to which the vector potential and the gradient of the

order parameter phase always come in the combination A

(c/2e) .

Using eqns (13.4) and (13.6) we can finally present eqn (13.9) in the form

(Larkin and Ovchinnikov 1986)

(13.10)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [261]-[265]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:05

where

(13.11)

Equation (13.10) is written in the form which does not assume a spherical Fermi

surface.

end p.261

In presence of a transport current, the force F

env

should be balanced by the

Lorentz force. The corresponding term eqn (12.14) can be incorporated into the

free energy exactly in the same way as we did it in Section 12.4. The force

balance becomes

(13.12)

Consider now the nonstationary part of the Green function. We write the Keldysh

function eqn (10.62) in frequency representation

where

(13.13)

As in eqn (11.21) we define the nonstationary function as

Using the particle–hole symmetry of the Green functions of the type of

eqn (10.68) with respect to the transformation

and p p one can

show that

(13.14)

is even in . Therefore, the first derivatives of and A in time drop out of eqn

(13.14). As a result, the nonequilibrium part of the total Green function in eqn

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 16:05

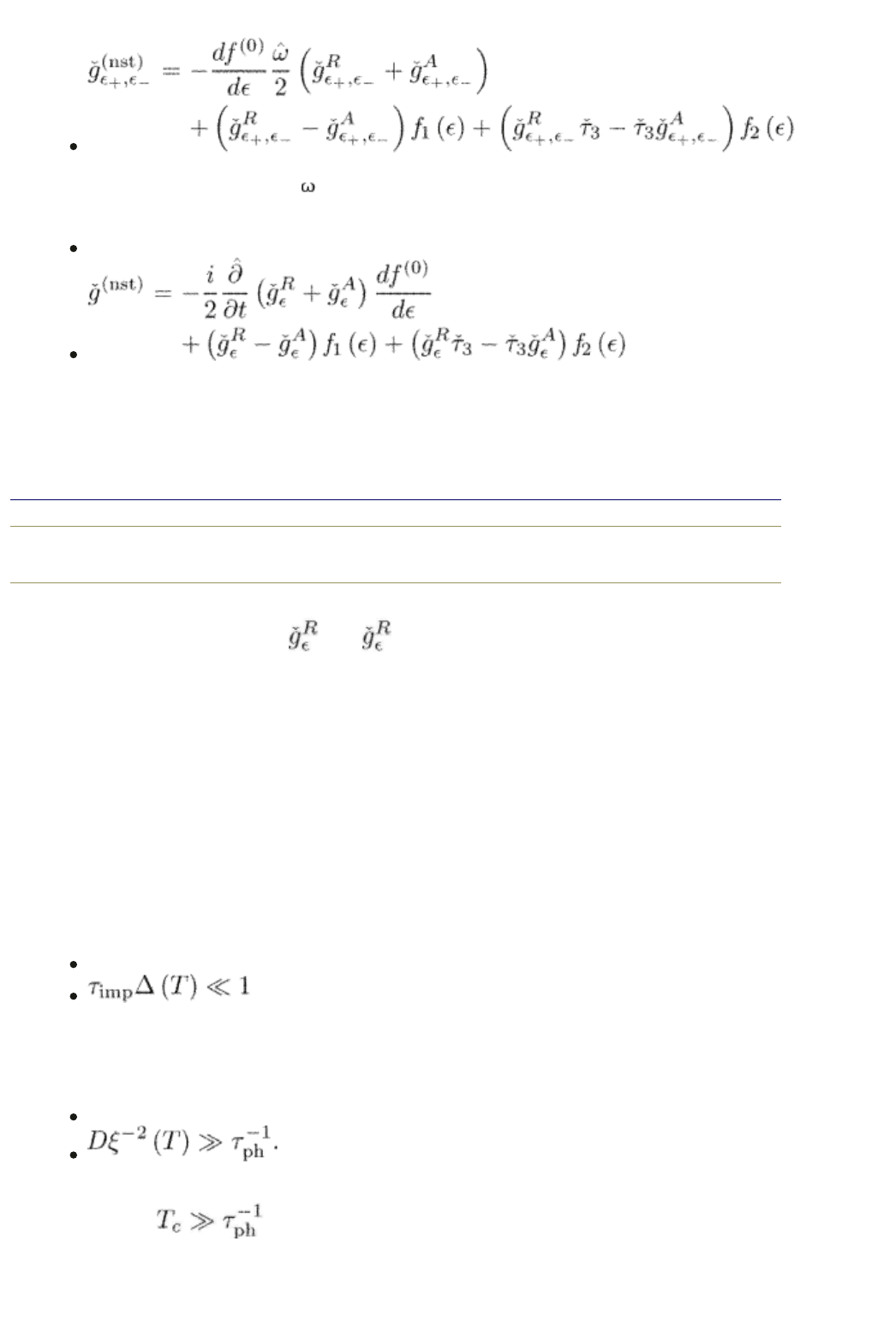
(13.10) can be written as

within the first-order terms in . Performing the Fourier transformation back to

the center-of-mass time, we get

(13.15)

where the gauge-invariant time-derivative is defined by eqn (10.32).

Equations (13.10) and (13.15) make the basis for calculations of the force on a

vortex within the microscopic theory. We shall use them for both dirty and clean

end p.262

superconductors in the following sections. We observe that the force is expressed

through the Green functions

and , as well as through the distribution

functions f

and f

. For the Green functions we can take their values for a steady

vortex array because f

and f

are themselves proportional to deviation from

equilibrium. In turn, f

and f

are solutions of kinetic equations which again

contain only the steady-state Green functions. The problem thus reduces to two

major steps. First, we need to find the Green functions for a stationary vortex.

Second, we solve the resulting kinetic equations and find the distribution function

of nonequilibrium excitations. The force can then be calculated performing the

necessary operations in eqn (13.10).

13.2. Diffusion controlled flux flow

In this section we consider dirty s-wave superconductors such that

(13.16)

for temperatures close to T

. Note that the gradients are not assumed to be small

any more in the sense of eqn (11.9). On the contrary, we concentrate on the

situation when the relaxation by diffusion is faster than the inelastic relaxation:

(13.17)

We recall also that the inelastic relaxation rate is much smaller than the critical

temperature,

. The temperature range when the condition eqn

(13.17) is fulfilled corresponds to

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 16:05

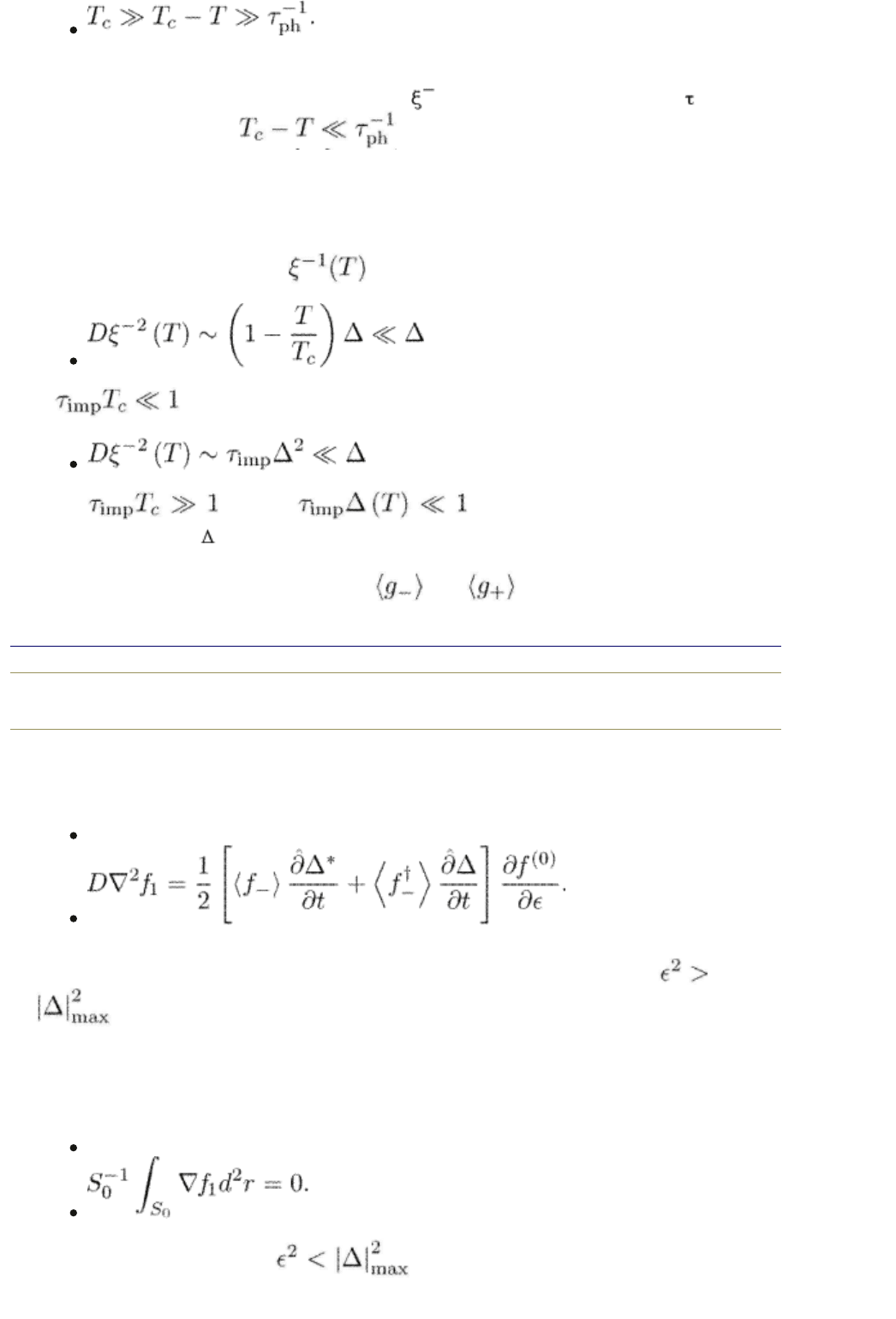
This condition is much less restrictive than what we have considered in the

previous chapter where, on the contrary, D

was assumed smaller than

and thus temperatures were required. The present conditions

are more “natural” and can easily be realized in experiments.

Due to eqn (13.16) the stationary Green functions for dirty superconductors are

determined by Usadel equations (5.97). For temperatures close to T

, the

diffusion terms in the Usadel equations can be neglected despite the fact that the

gradients are of the order of

. Indeed,

if , or

when but still . The diffusion terms are thus

small compared to

under conditions of eqn (13.16). We also neglect the small

inelastic pair-breaking. As a result, we obtain the adiabatic expressions (10.104)

and (10.105) for the regular functions

and .

end p.263

Under these conditions, we can use kinetic equations (10.107) and (10.108)

derived for adiabatic Green functions. Neglecting the inelastic scattering we

obtain

(13.18)

The boundary conditions for eqn (13.18) are formulated as follows. For

, the quasiparticle Green functions extend over long distances from the

vortex cores. For a periodic vortex array, the distribution function f

translationally invariant with the period of the vortex array. Thus it should not

increase at large distances from the vortex. This requires that the average

gradient of f

vanishes

(13.19)

However, for particles with , large distances are not accessible.

The boundary conditions are imposed at the surface determined by the condition

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:05

(13.20)

beyond which the particle cannot penetrate. The conditions can be obtained from

eqns (10.106) and (13.18). Integrating eqn (13.18) across the surface in eqn

(13.20) one finds that the derivative

along its normal is continuous at this

surface. At the same time, eqn (10.106) implies that, at the side of the surface

where |

| < | (r)|, the gradient vanishes because g = 0. Therefore, one should

also have

(13.21)

at the other side of the surface defined by eqn (13.20), where

is the

derivative along the normal to the surface. Equations (13.19) and (13.21) are

the required boundary conditions to eqn (13.18) (Larkin and Ovchinnikov 1986).

The expression for the force eqn (13.10) contains the nonstationary part of the

current eqn (13.6) proportional to the energy integral of g

. According to eqn

(10.108), we have

The integral diverges logarithmically at due to a square-root singularity in

. This divergence is cut off at ~ D

. However, the prefactor at the

logarithm is proportional to

/T; it is thus small near the critical temperature.

The main contribution, however, comes from the region of energies

~ T. For

such energies,

. At the same time, the function f

is proportional to

/T (compare with eqn (11.19)) and can be neglected. As a result, we again

have

end p.264

According to eqn (13.18), the distribution function is, by the order of magnitude,

and gives a much larger contribution to the nonstationary Green function than

the first term in the r.h.s. of eqn (13.15). Therefore, neglecting f

we have

Equation (13.10) becomes

(13.22)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:05

The next step is to solve the kinetic equation (13.18) for f

. Consider first the

limit of low magnetic fields. For well-separated vortices, the order parameter

magnitude depends only on the distance from the vortex axis. Equation (13.18)

for

> | |

takes the form

We put

and obtain for w ( )

The solution regular at 0 is

The constant should be found from the boundary conditions. Denote d a constant

arbitrary vector. We have

end p.265

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:05

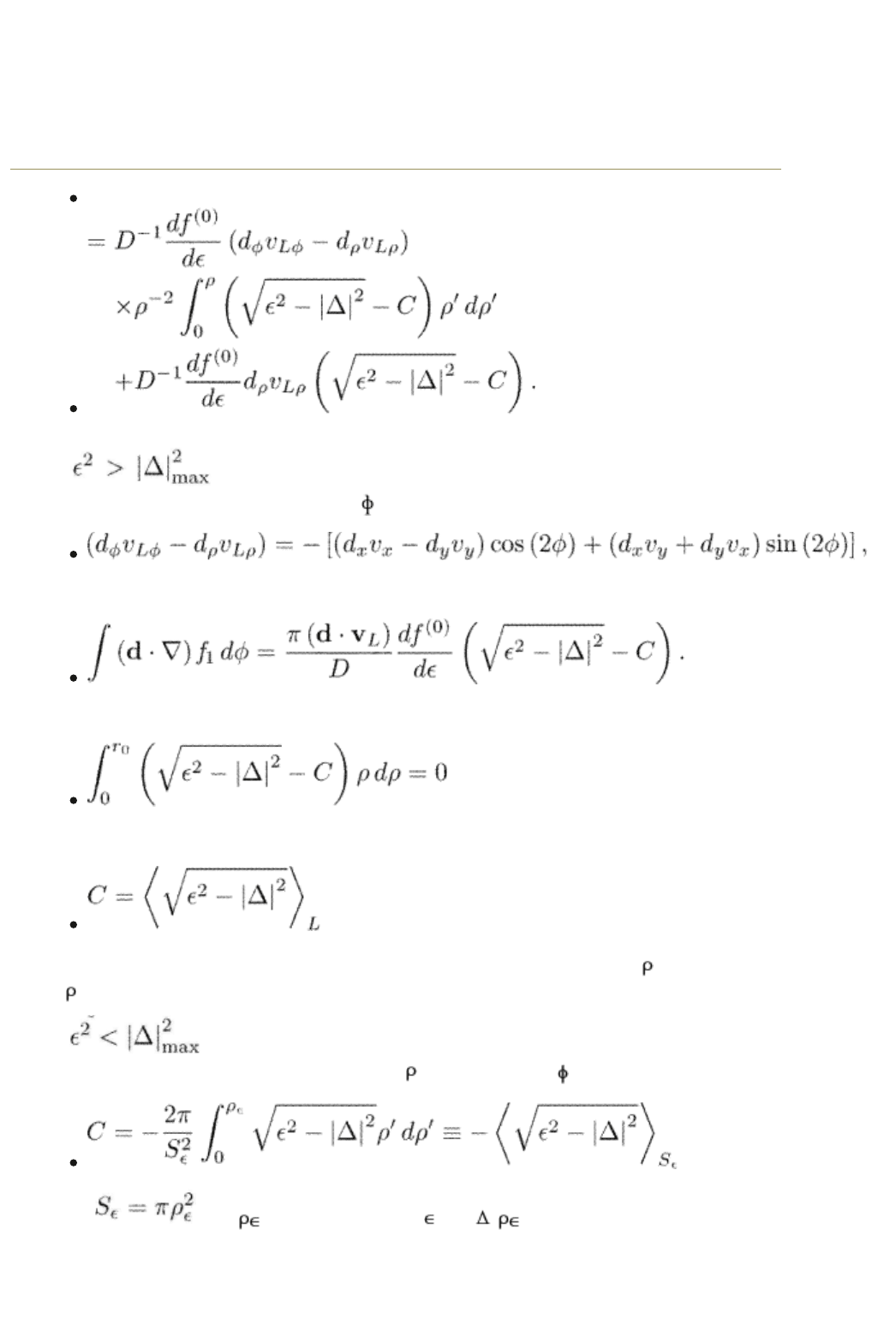
(13.23)

For , the boundary condition has the form of eqn (13.19). We

average eqn (13.23) over the angles

Since

the first term in the r.h.s. of eqn (13.23) vanishes. The second term gives

Integrating now over the radial distance, we have from eqn (13.19)

where r

is the radius of the vortex lattice unit cell. Thus

where the average is taken over the vortex unit cell. The function w ( ) vanishes

for

= r

For

, we use the boundary condition eqns (13.21). Equation

(13.23) taken for the derivative along the

direction with d = 0 gives

where and is determined by | | = | ( )|.

Now we calculate the force on a vortex. The balance of the Lorentz force and the

force in eqn (13.22) reads

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [266]-[270]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:06