Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

(12.6)

where S

/B is the area occupied by each vortex.

end p.234

All the values in eqn (12.4) can easily be calculated if the vortex velocity v

small. To calculate the time-derivative of the order parameter and of the vector

potential we note that, for a small vortex velocity,

(12.7)

where

and A

are the values for a static vortex, and

and A

are small

corrections. Therefore, within the main terms in the vortex velocity v

, we can

write

(12.8)

The scalar potential is to be found from eqn (1.80). For small v

it contains only

the static vortex order parameter.

Let us calculate the average electric field. The local electric field is

(12.9)

The last term here is nonzero for a moving vortex. Indeed,

(12.10)

Here is the unit vector along the vortex axis in the positive direction of its

circulation. The vortex circulation is determined by the sense of the phase

increment, it coincides with the magnetic field direction for positive charge of

carriers and is antiparallel to it for negative carriers:

, see

Section 1.1.2. We now average eqn (12.9) over the vortex array. Since

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 16:01

the average of this term vanishes because the gauge-invariant vector potential

is a bounded oscillating function (periodic for a periodic vortex array). Its

value at the boundary of a region occupied by each vortex, i.e., at the boundary

of the vortex unit cell is zero, see eqn (1.40) on page 11. The average of

vanishes, too, since is also a bounded oscillating function periodic for a regular

vortex lattice. It turns to zero at the boundary of the vortex unit cell because of

the Josephson relation, eqn (11.49). The only term which survives is the last

term in eqn (12.9). Equation (12.10) gives

(12.11)

which is the Faraday’s law.

end p.235

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 16:01

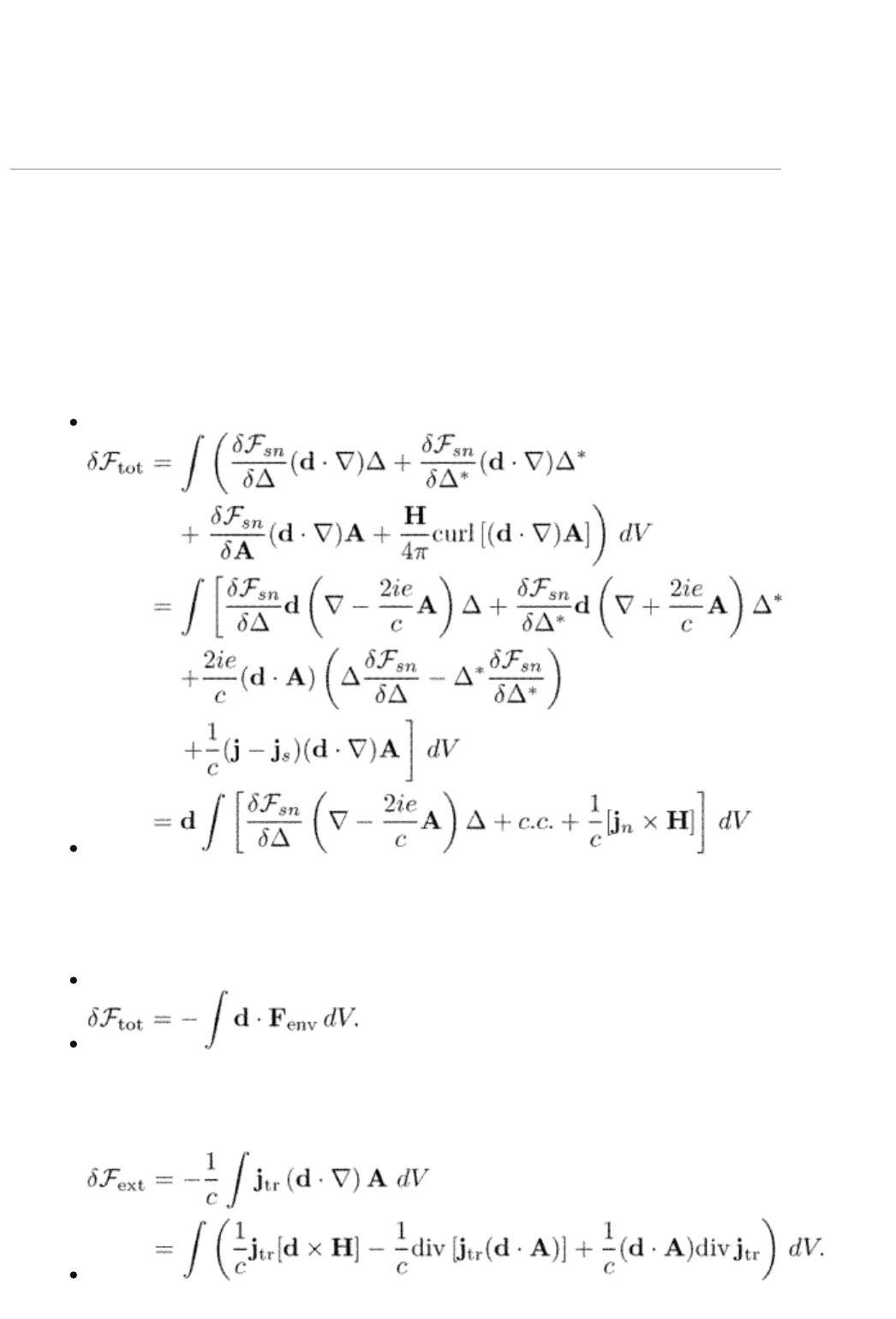
Now we can calculate W. It is more instructive, however, to consider another

useful relation which follows from the TDGL equations. It is expression for the

force which acts on a moving vortex.

12.4 Force balance

Let us shift our vortex by a small arbitrary constant vector d and calculate the

variation of the free energy caused by such a displacement. During the derivation

we neglect surface contributions. We have

(12.12)

where we use eqn (1.76) and the charge neutrality divj = 0.

Variation of the free energy determines the force which acts on a moving vortex

from the environment

(12.13)

It should be balanced by external Lorentz force due to the transport current. To

include this force we add the free energy due to the transport current which is

supplied by the external source. Its variation due to the vortex displacement is

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [236]-[240]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:01

On the next step, we omit the surface term and use that divj

= 0. We find

(12.14)

Conservation of plus the external energy implies its translation invariance

end p.236

It gives the balance of forces acting on a moving vortex of a unit length

(12.15)

where F

is the Lorentz force eqn (12.1). We use the fact that d is an arbitrary

vector. In other words,

(12.16)

Here the integration is over the unit cell of the vortex array.

To summarize, in eqns (12.12) or (12.16) the Lorentz force is balanced by the

force produced by the interaction with the environment. The latter is proportional

to the vortex velocity since the time-derivative, electric field and the scalar

potential are all proportional to v

Note that the dissipation function integrated over the unit cell can be again

obtained if we multiply eqn (12.16) with the vortex velocity v

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 16:01

The left-hand side of this equation can be expressed through the effective flux

flow conductivity. We write

since S

/B. The right-hand side is also proportional to . The

coefficient of proportionality determines

end p.237

12.5 Flux flow

12.5.1 Single vortex: Low fields

Consider first a single vortex provided 1 and H H

. In this case we can

neglect the magnetic field and the vector potential compared to the gradient of

the order parameter since

We have from eqn (12.15)

(12.17)

The order parameter magnitude | | = f( ) for a static vortex satisfies eqn

(1.48). To calculate the integrals in eqn (12.17) we also need to know the gauge

invariant potential

. It satisfies eqn (11.48) whence

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 16:01

since (| |/ ) = f

for the usual TDGL model, eqn (1.80). The potential

should he finite. Therefore, we require

(12.18)

for 0. We put and

(12.19)

where is the azimuthal angle in the cylindrical frame ( , , z). The function

satisfies the equation

(12.20)

where , see eqn (1.81). The condition eqn (12.18) requires

for . We see that a moving vortex induces a dipole-like

scalar potential proportional to the vortex velocity.

The two terms under the integral in eqn (12.17) represent two different

mechanisms of dissipation during the vortex motion exactly as the two

corresponding terms in the dissipation function eqn (12.4). The first term is the

Tinkham’s mechanism (Tinkham 1964) of relaxation of the order parameter: Due

to the motion of a vortex, the order parameter at a given point varies in time

which produces a relaxation accompanied by dissipation. The second is the

so-called

end p.238

Bardeen and Stephen (1965) contribution. It accounts for normal currents

flowing through the vortex core.

Equation (12.17) gives

(12.21)

Here we have restored the arbitrary vector d that appears in eqns (12.12) and

(12.14) to make the calculations more convenient. The transport current is

(12.22)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 16:01

Here

(12.23)

Expressing v

, through we obtain the flux flow conductivity

With the microscopic values of and taken for dirty superconductors, we

find

(12.24)

As already mentioned, the first term in eqn (12.23) is due to the dissipation

caused by relaxation of the order parameter after passage of a vortex, while the

second one comes from the normal-current dissipation in the vortex core. In the

TDGL model with u ~ 1, both mechanisms give comparable contributions to

The numerical calculations using the vortex order parameter obtained by solving

the GL equation give for the first term (see the review by Gor’kov and Kopnin

(1975) and references therein)

which is independent of u. The second term, however, does depend on u. For

example, for u = 5.79 we have

To calculate a

we need first to solve eqn (12.20). In this case, the total

coefficient is a

0.502. The flux flow conductivity becomes

end p.239

(12.25)

It is close to t ho expression

/B known as the Bardeen–Stephen model

(Bardeen and Stephen 1965). This simple prediction implies that the flux flow

resistivity is just a normal-state resistivity times the fraction of space occupied by

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 16:01

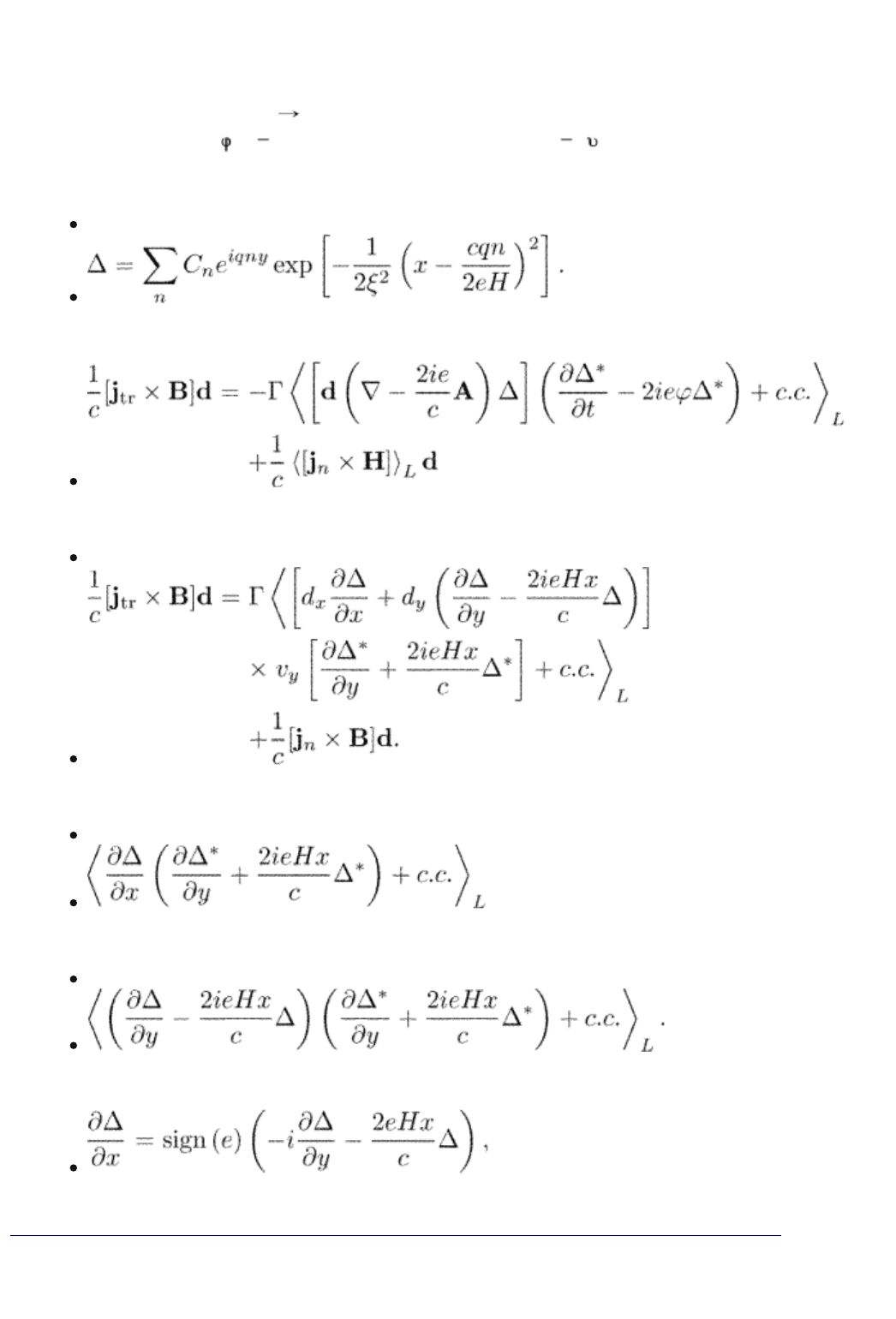
vortex cores.

12.5.2 Dense lattice: High fields

Consider now high fields, H H

. We put A = (0, Hx, 0), and choose the static

potential in the form

= E

x, where the electric field E

= (

/c)H is

homogeneous in the leading approximation. Recall that the static order

parameter in the vicinity of the upper critical field, see Section 1.1.2, eqn (1.36):

(12.26)

Equation (12.16) gives

where d is again an arbitrary vector. We have

(12.27)

We need to calculate the averages

(12.28)

and

(12.29)

We make use of the identities

end p.240

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 16:01

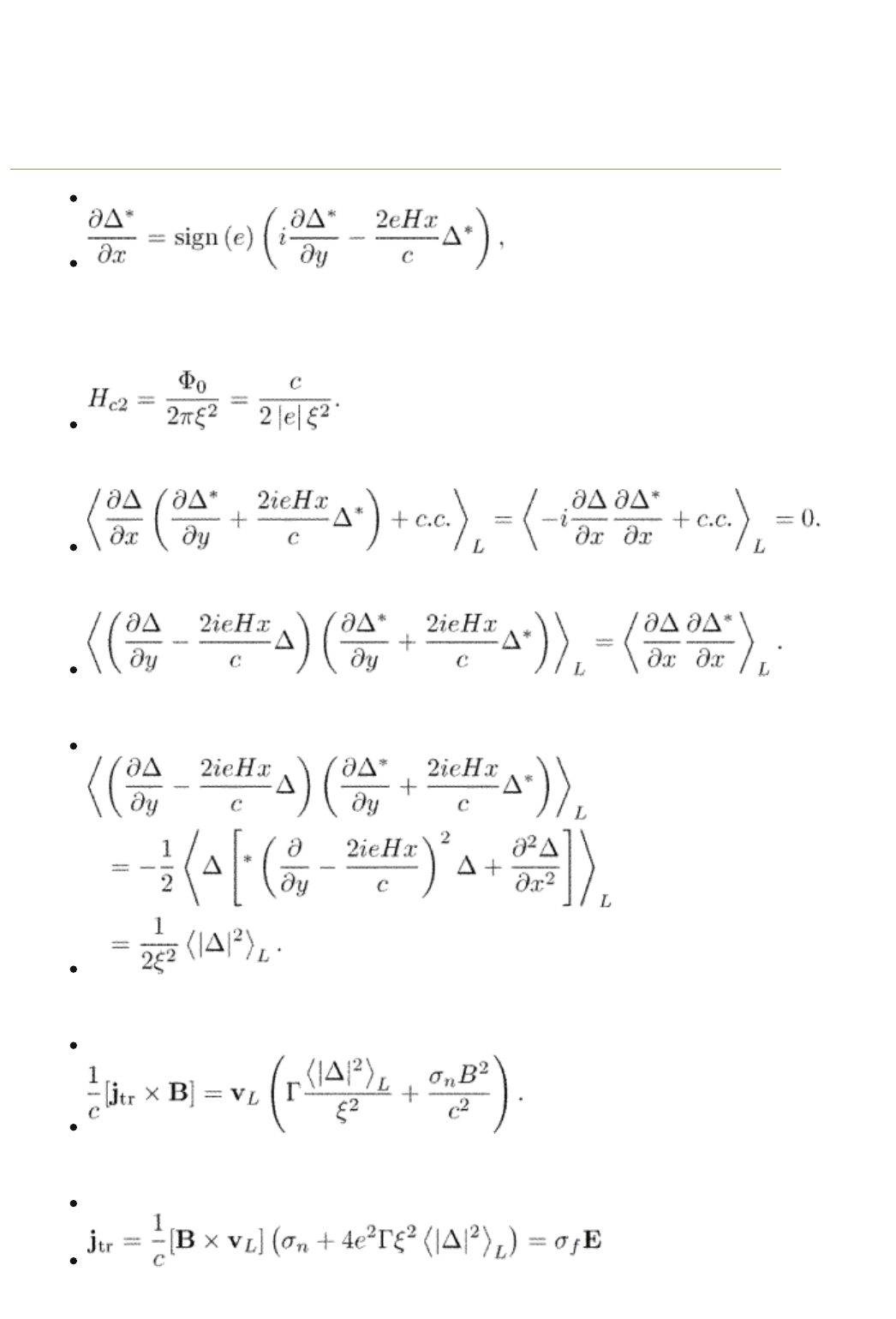
(12.30)

derived for the order parameter from eqn (12.26). The sign of the electronic

charge appears because the upper critical field contains the modulus of the

electronic charge,

For the average in eqn (12.28) we obtain

The second average is

Therefore

(12.31)

We obtain from eqn (12.27)

(12.32)

Finally

(12.33)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [241]-[245]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 16:02

where the flux flow conductivity is

(12.34)

The average magnitude of the order parameter is from eqn (1.43)

Therefore

end p.241

(12.35)

Equations (12.25) and (12.35) determine the flux flow conductivity in the limits

of low and high magnetic fields. The effective resistivity

is linear in

the magnetic field in both limits. However, the slope at low fields is smaller than

that for H

. Indeed,

For practical values of u 5.79, one has 2/ua < u/2

It is interesting to note that the linearized TDGL equation has an analytical

solution describing the moving vortex lattice (Schmid 1966). Indeed, the TDGL

equation

(12.36)

with A = (0, Hx, 0) and = E

x has the solution within the first-order terms in

(12.37)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 16:02