Коловский Ю В. Метрология, стандартизации и технические измерения
Подождите немного. Документ загружается.


определителя D столбца и строчки, на пересечении которых находится дан-
ный элемент),
- оценка дисперсии условных уравнений.
Оценка дисперсии условных уравнений вычисляется по формуле
(1.223)
Метод наименьших квадратов дает возможность найти оценки изме-
ряемых величин и оценить их средние квадратические отклонения.
Доверительные интервалы для истинных значений измеряемых вели-
чин строят на основе распределения Стьюдента
*
. Число степеней свободы
при этом для всех измеряемых величин равно n-m.
Приведение линейных неравноточных условных уравнений к рав-
ноточным
При неравноточных условных уравнениях наиболее вероятную сово-
купность значений неизвестных A, B, C, ... получим, если минимизировать
(1.224)
где
- вес i-го условного уравнения.
Введение весов равносильно умножению условных уравнений на
.
В итоге в коэффициенты при неизвестных в нормальных уравнениях войдут
сомножители
.
Так, первое из системы нормальных уравнений (104) примет вид
(1.225)
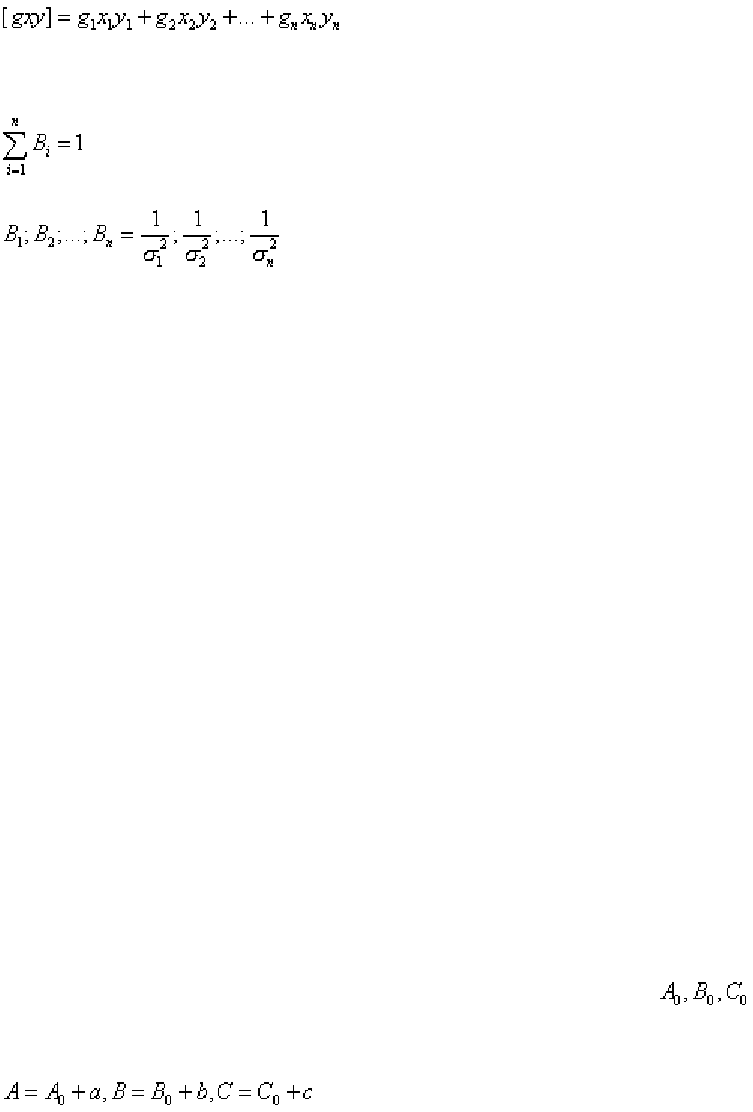
Аналогично изменятся и все остальные уравнения. При этом каждый
коэффициент уравнения представляет собой сумму членов вида
(1.226)
Веса условных уравнений находят из условий:
(1.227)
(1.228)
Следовательно, для решения задачи нужно знать дисперсии условных
уравнений. Если веса определены (или выбраны), то после приведенных пре-
образований дальнейшее решение задачи выполняем в полном соответствии
с изложенным в 4.1. и в итоге получаем оценки измеряемых величин и их
средние квадратические отклонения. Однако обычно веса определяются при-
ближенно.
Линеаризация нелинейных условных
уравнений
Метод наименьших квадратов по ряду причин принципиального харак-
тера используется только для линейных условных уравнений. Поэтому нели-
нейные условные уравнения желательно преобразовывать к линейному виду.
Общий метод решения данной задачи основан на допущении, что несо-
вместность условных уравнений невелика, т.е. их невязки малы. Тогда, взяв
из системы условных
уравнений столько уравнений, сколько у нас неизвест-
ных, их решением находим начальные оценки неизвестных
. Полагая
далее, что
, (1.229)
и подставляя эти выражения в условные уравнения, раскладываем ус-
ловные уравнения в ряды. Пусть
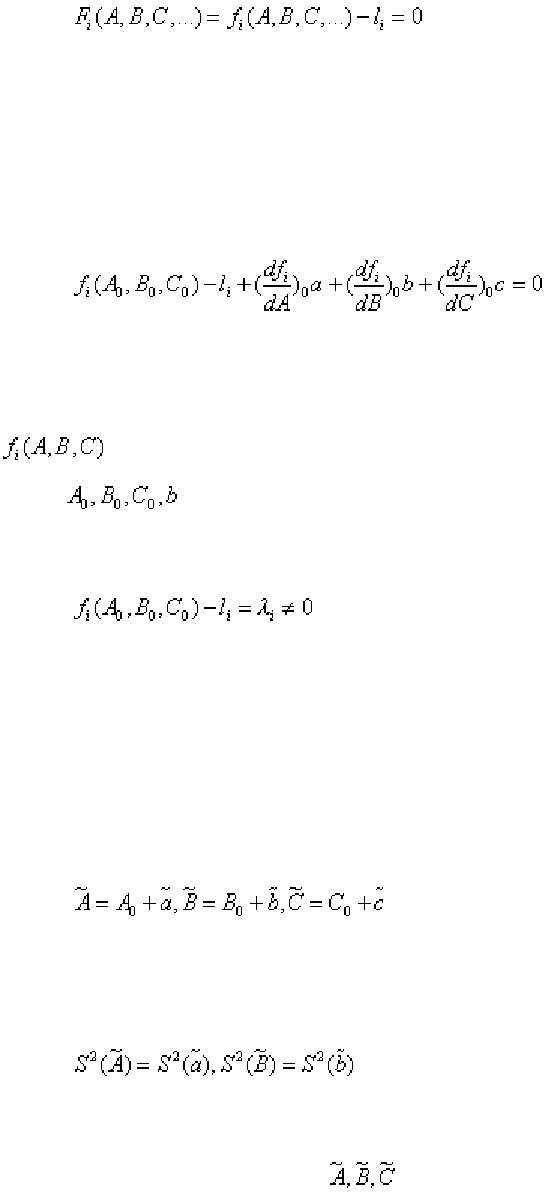
. (1.230)
Тогда, сохраняя лишь члены с первыми степенями поправок a,b,c, по-
лучим
(1.231)
Частные производные находим путем дифференцирования функции
по A,B,C соответственно, а затем в полученные формулы подстав-
ляем
, находим их числовые значения. Кроме того,
(1.232)
Таким образом, мы получаем систему линейных условных уравнений
относительно a,b,c. Решение ее дает нам их оценки и средние квадратические
отклонения. Тогда
(1.233)
Поскольку A , B , C - неслучайные величины, то
и т.д. (1.234)
В принципе получив
можно сделать второе прибилжение и т.д.
Наряду с рассмотренным общим методом линеаризации условных
уравнений пользуются также методом подстановок. Так, если условное урав-
нение имеет вид:

(1.235)
где x,y,z - непосредственно измеряемые величины; A, B требуется оп-
ределить, то можно сделать подстановку:
(1.236)
Тогда получим линейное условное уравнение
(1.237)
Pешение этих уравнений дает
и оценки их дисперсий, используя ко-
торые, затем можем найти искомые величины A, B.
Метод подстановок удобен, однако возможен не во всех случаях.
Пример. Рассмотрим приведенный в начале пример совокупных изме-
рений емкости двух конденсаторов. Результаты прямых измерений следую-
щие:
= 0,2071 мкФ, = 0,2056 мкФ.
= 0,4111 мкФ, = 0,1035 мкФ;
Последнее уравнение - нелинейное. Разложим его в ряд Тейлора, для
чего найдем сначала частные производные:
(1.238)
и аналогично

(1.239)
Поскольку
, то можно написать:
(1.240)
Разложение в ряд выполним для точки с координатами
. Получим:
(1.241)
=0,249
Условные уравнения найдем, полагая :
Теперь вычислим коэффициенты нормальных уравнений:
[xx] = 2,062e [xy] = 1,0625;
[yy] = 2,063; [xl] = - 0,001738, [yl] =- 0,002237.
Нормальными уравнениями будут:
2,062
+ 1,0625 = - 0,001738;
1,0625
+ 2,0630 = - 0,002237.
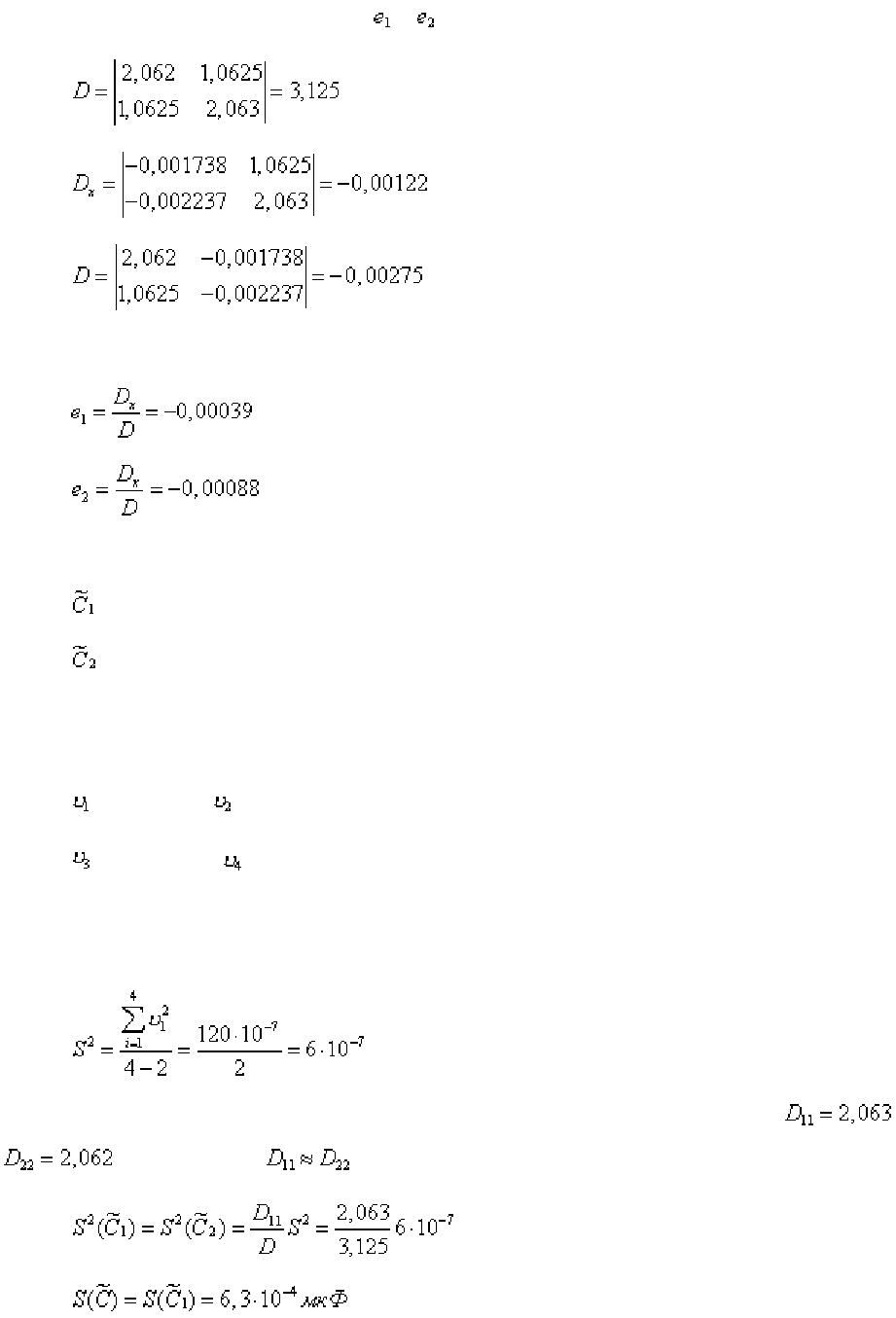
Теперь находим искомые и . Согласно (7-5) вычисляем:
Отсюда находим:
Следовательно,
=0,2070-0,00039=0,20661 мкФ
=0,2060-0,00088=0,20512 мкФ
Остаточные невязки условных уравнений найдем, подставив найден-
ные оценки неизвестных в условные уравнения:
=0,00049, =0,00058
=-0,00063, =0,0048
Теперь по формуле (107) можно вычислить оценку дисперсии услов-
ных уравнений
Алгебраическими дополнениями определителя D будут
и
. Поскольку , то
Рассмотренный метод измерения емкостей конденсаторов, по-
видимому, был выбран для того, чтобы несколько уменьшить систематиче-
скую погрешность измерения, различную в разных точках диапазона измере-
ния; для уменьшения случайной составляющей погрешности было бы доста-
точно измерение каждой емкости выполнить с многократными наблюдения-
ми. Если приведенное предположение справедливо, то несовместность ус-
ловных уравнений
обусловлена тем, что систематические погрешности были
разными в разных точках диапазона измерения. В этом случае вероятностная
модель не оправдана и среднее квадратическое отклонение вряд ли можно
считать показательным параметром погрешности измерения.
Вопросы к лекции:
1. Линейные косвенные измерения?
2. Вычисление доверительных границ неисключенной систе-
матической погрешности результата косвенных измерений?
3. Нелинейные косвенные измерения?
4. Метод наименьших квадратов и общая схема его примене-
ния?
5. Приведение линейных неравноточных условных уравнений
к равноточным?
6. Линеаризация нелинейных условных уравнений?
Лекция 6.
Тема 3. Основы теории погрешностей.
План лекции:
Классификация составляющих погрешности измерения: методи-
ческая и инструментальная, аддитивная и мультипликативная,
основная и дополнительная, статическая и динамическая, систе-
матическая и случайная составляющие.
Грубые погрешности и промахи.
Современные принципы нормирования и оценивания показателей
точности средств измерения и представления результатов изме-
рения.
Погрешности измерений
Основные понятия и определения
При анализе измерений следует четко разграничивать два понятия: ис-
тинные значения физических величин и их эмпирические проявления ─ ре-
зультаты измерений.
Истинные значения физических величин ─ это значения, идеальным
образом отражающие свойства данного объекта как в количественном, так и
в качественном отношении. Они не
зависят от средств нашего познания и яв-
ляются абсолютной истиной.
Результаты измерений, напротив, являются продуктами нашего позна-
ния. Представляя собой приближенные оценки значений величин, найденные
путем измерения, они зависят не только от них, но еще и от метода измере-
ния, от технических средств, с помощью которых проводятся измерения, и от
свойств органов чувств наблюдателя, осуществляющего измерения [3].
Как отмечалось ранее, разница
между результатами измерения X' и
истинным значением Q измеряемой величины называется погрешностью из-
мерения:
QX '
(1.2)
Но поскольку истинное значение Q измеряемой величины неизвестно,
то неизвестны и погрешности измерения, поэтому для получения хотя бы
приближенных сведений о них необходимо в формулу (1) вместо истинного
значения подставлять так называемое действительное значение.
Под действительным значением физической величины мы будем пони-
мать ее значение, найденное экспериментально и настолько приближающееся
к истинному
, что для данной цели оно может быть использовано вместо него.
Причинами возникновения погрешностей являются: несовершенство
методов измерений, технических средств, применяемых при измерениях, и
