Коловский Ю В. Метрология, стандартизации и технические измерения

Подождите немного. Документ загружается.





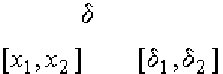
)1()2()(

xFxFdxxf

(1.10)

здесь вероятность попадания случайной величины в интервал от

до

x .

От дифференциальной функции распределения легко перейти к инте-

гральной путем интегрирования:







dx)x(p)x(F

(1.11)

Размерность плотности распределения вероятностей, как это следует из

формулы (7), обратна размерности измеряемой величины, поскольку сама

вероятность ─ величина безразмерная.

Используя понятия функций распределения, легко получить выражения

для вероятностей того, что результат наблюдений Х или случайная погреш-

ность

примет при проведении измерения некоторое значение в интервале

или . В терминах интегральной функции распределения имеем:

);(F)(F}{P}{P)(P

);x(F)x(F}xX{P}xX{P)xXx(P

121221

1x2x1221







(1.12)

т. е. вероятность попадания результата наблюдений или случайной погреш-

ности в заданный интервал равна разности значений функции распределения

на границах этого интервала.

Заменяя в полученных формулах интегральные функции распределения

на соответствующие плотности распределения вероятностей согласно выра-

жению (7), получим формулы для искомой вероятности в терминах диффе-

ренциальной функции распределения:







21 2

xxx

xxx21

dx)x(pdx)x(pdx)x(p)xXx(P

(1.13)















d)(pd)(pd)(p)(P

(1.14)

Таким образом, вероятность попадания результата наблюдения или

случайной погрешности в заданный полуоткрытый интервал равна площа-

ди, ограниченной кривой распределения, осью абсцисс и перпендикулярами

к ней на границах этого интервала. Необходимо отметить, что результаты на-

блюдений в значительной степени сконцентрированы вокруг истинного зна-

чения измеряемой величины и по мере приближения к

нему элементы веро-

ятности их появления возрастают. Это дает основание принять за оценку ис-

тинного значения измеряемой величины координату центра тяжести фигуры,

образованной осью абсцисс и кривой распределения, которую называемуют

математическим ожиданием результатов наблюдений:









mdx)x(xp]X[M

(1.15)

Дадим более строгое определение постоянной систематической и слу-

чайной погрешностям.

Систематической постоянной погрешностью называется отклонение

математического ожидания результатов наблюдений от истинного значения

измеряемой величины:

Q]X[M 

(1.16)

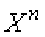
а случайной погрешностью − разность между результатом единичного

наблюдения и математическим ожиданием результатов:

]X[MX 

(1.17)

В этих обозначениях истинное значение измеряемой величины составляет



 XQ

(1.18)

Моменты случайных погрешностей

Функция распределения является самым универсальным способом опи-

сания поведения случайных погрешностей. Однако для определения функций

распределения необходимо проведение весьма кропотливых научных иссле-

дований и обширных вычислительных работ. Поэтому к такому способу опи-

сания случайных погрешностей прибегают иногда при исследовании прин-

ципиально новых мер и измерительных приборов.

Значительно чаще бывает достаточно охарактеризовать случайные по-

грешности с помощью ограниченного числа специальных величин, называе-

мых моментами [5].

Начальным моментом n-го порядка результатов наблюдений называет-

ся интеграл вида







 dx)x(px]X[M)X(a

(1.19)

представляющий собой математическое ожидание степени

При n = 1









xx1

mdx)x(xp]X[M)X(a

(1.20)

т. е. первый начальный момент совпадает с математическим ожиданием

результатов измерений.

Центральным моментом n-го порядка результатов наблюдений называ-

ется интеграл вида

dx)x(p)mx(}]mX{[M)X(









(1.21)

Вычислим первый центральный момент:















 0mmdx)x(pmdx)x(xpdx)x(p)mx()X(

xxxxxxx1

(1.22)

Таким образом, первый центральный момент результатов наблюдений

равен нулю. Важно отметить, что начальные и центральные моменты случай-

ных погрешностей совпадают между собой и с центральными моментами ре-

зультатов наблюдений, поскольку математическое ожидание случайных по-

грешностей равно нулю.

Особое значение наряду с математическим ожиданием результатов на-

блюдений имеет второй центральный момент

, называемый дисперсией ре-

зультатов наблюдений.

При n = 2













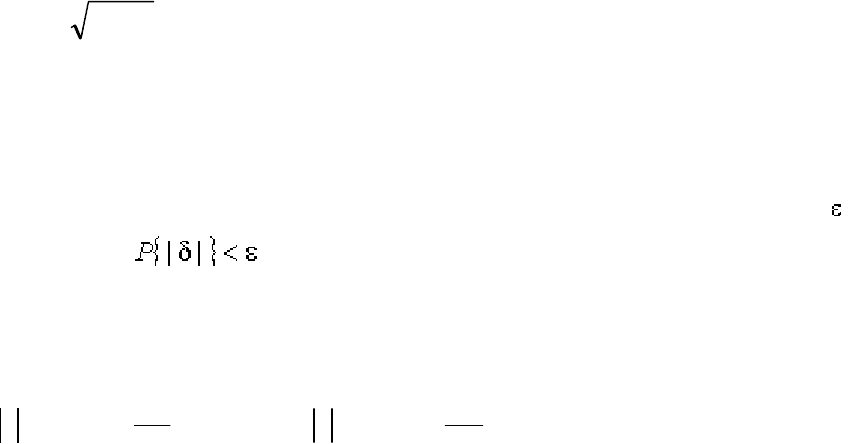
 d)(pdx)x(p)mx(}]mX{[M][D]X[D

(1.23)

Дисперсия D[X] случайной погрешности равна дисперсии результатов

наблюдений и является характеристикой их рассеивания относительно мате-

матического ожидания.

Если математическое ожидание результатов наблюдений можно рас-

сматривать в механической интерпретации как абсциссу центра тяжести фи-

гуры, заключенной между кривой распределения и осью Ох, то дисперсия

является аналогом момента инерции этой фигуры

относительно вертикаль-

ной оси, проходящей через центр тяжести.

Дисперсия имеет размерность квадрата измеряемой величины, поэтому

она не совсем удобна в качестве характеристики рассеивания. Значительно

чаще в качестве последней используется положительное значение корня

квадратного из дисперсии, называемое средним квадратическим отклонением

результатов наблюдений:

]X[D



(1.24)

С помощью среднеквадратического отклонения можно оценить вероят-

ность того, что при однократном наблюдении случайная погрешность по аб-

солютной величине не превзойдет некоторой наперед заданной величины

т. е. вероятность

. Для этого рассмотрим формулу, известную как

неравенство Чебышева:

1}{P







или

1}{P







(1.25)

Полагая

3



, можно найти вероятность того, что результат одно-

кратного наблюдения отличается от истинного значения на величину, больше

утроенного среднеквадратического отклонения, т. е. вероятность того, что

случайная погрешность окажется больше



11.0

)3(

}{P







(1.26)

Вероятность того, что погрешность измерения не превысит

3

, составит

соответственно

89.011.01}{P 

(1.27)

Неравенство Чебышева дает только нижнюю границу для вероятности

}{P

, меньше которой она не может быть ни при каком распределении.

Обычно

 3}{P

значительно больше 0,89. Так, например, в случае нор-

мального распределения погрешностей эта вероятность составляет 0,9973.

Математическое ожидание и дисперсия являются наиболее часто при-

меняемыми моментами, поскольку они определяют самые важные черты рас-

пределения: положение центра распределения и степень его разбросанности.

Для более подробного описания распределения используются моменты более

высоких порядков.

Третий момент

случайных погрешностей служит характеристикой

асимметрии или скошенности распределения. В общем случае любой нечет-

ный момент случайной погрешности характеризует асимметрию распределе-

ния. Действительно, если распределение обладает свойством симметрии, то

все функции вида

)(p





, где s = l, 3, 5... являются нечетными функциями



Поэтому все нечетные моменты, являющиеся интегралами этих функ-

ций в бесконечных пределах, должны равняться нулю. Отличие этих момен-

тов от нуля как раз и указывает на асимметрию распределения. Простейшим

из нечетных моментов является третий момент

][





. Чтобы получить без-

размерную характеристику, третий момент делят на третью степень средне-

квадратического отклонения и получают коэффициент асимметрии или про-

сто асимметрию

Sk распределения:

][







(1.28)

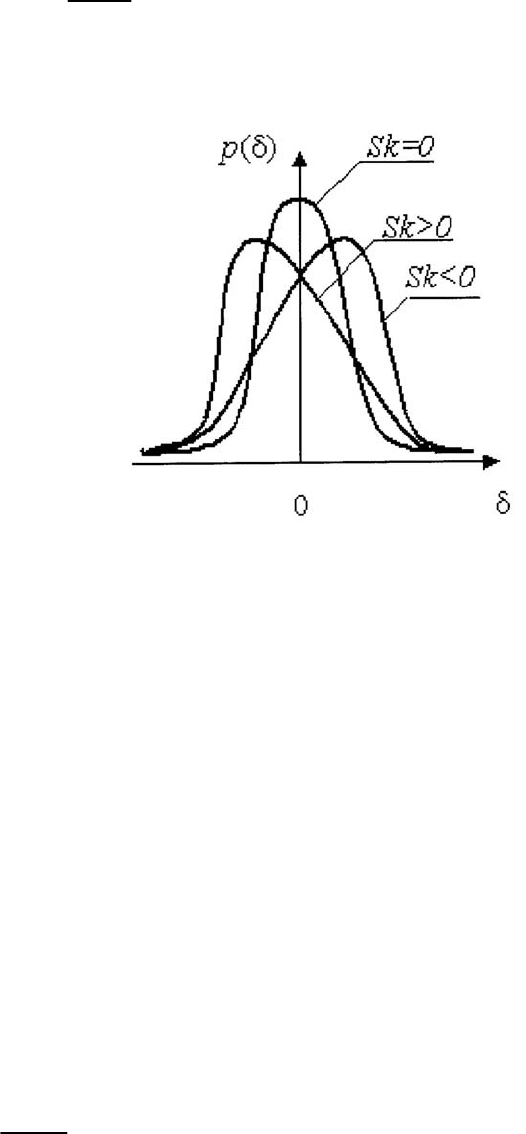
Рисунок 1.3 – Примеры распределения случайных погрешностей с по-

ложительной, отрицательной и нулевой асимметрией

Для иллюстрации сказанного на рисунке 3 приведены три кривые рас-

пределения случайных погрешностей с положительной, отрицательной и ну-

левой асимметрией.

Четвертый момент служит для характеристики плосковершинности или

островершинности распределения случайных погрешностей. Эти свойства

описываются с помощью эксцесса − безразмерной

характеристики, опреде-

ляемой выражением

][









(1.29)

Число 3 вычитают из отношения

][





потому, что для широко распро-

страненного нормального распределения погрешностей

x3][

 . Таким об-

разом, для нормального распределения эксцесс равен нулю, более плоско-

вершинные распределения обладают отрицательным эксцессом, более остро-

вершинные - положительным.

Виды распределения результатов наблюдения и случайных погрешно-

стей

Случайная погрешность измерения образуется под влиянием большого

числа факторов, сопутствующих процессу измерения. В каждой конкретной

ситуации работает свой механизм образования погрешности. Поэтому

есте-

ственно предположить, что каждой ситуации должен соответствовать свой

тип распределения погрешности. Однако во многих случаях имеются воз-

можности еще до проведения измерений сделать некоторые предположения о

форме функции распределения, так что после проведения измерений остается

только определить значения некоторых параметров, входящих в выражение

для предполагаемой функции распределения.

Случайная погрешность

характеризует неопределенность наших зна-

ний об истинном значении измеряемой величины, полученных в результате

проведенных наблюдений. Согласно К. Шеннону мерой неопределенности

ситуации, описываемой случайной величиной X, будет энтропия [6].







 dx)x(pln)x(pH

(1.30)

являющаяся функционалом дифференциальной функции распределе-

ния

)x(p

. Можно предположить, что любой процесс измерения формируется

таким образом, что неопределенность результата наблюдений оказывается

наибольшей в некоторых пределах, определяемых допускаемыми значениями

погрешности. Поэтому наиболее вероятными должны быть такие распреде-

ления

)x(p

, при которых энтропия обращается в максимум.

Для выявления вида наиболее вероятных распределений рассмотрим

несколько наиболее типичных случаев [5].

В классе распределений результатов наблюдений

)x(p

, обладающих

определенной зоной рассеивания между значениями

х = b и х = а шириной

b−а=2а, найдем такое, которое обращает в максимум энтропию





dx)x(pln)x(pH

(1.31)

при наличии ограничивающих условий:







mdx)x(xp

1dx)x(p

0)x(p

(1.32)

где





− математическое ожидание результатов наблюдений. Решение

поставленной задачи находится методом множителей Лагранжа.

Искомая плотность распределения результатов наблюдений описывает-

ся выражением





















xb,0

,bxa,

,ax,0

)x(p

(1.33)

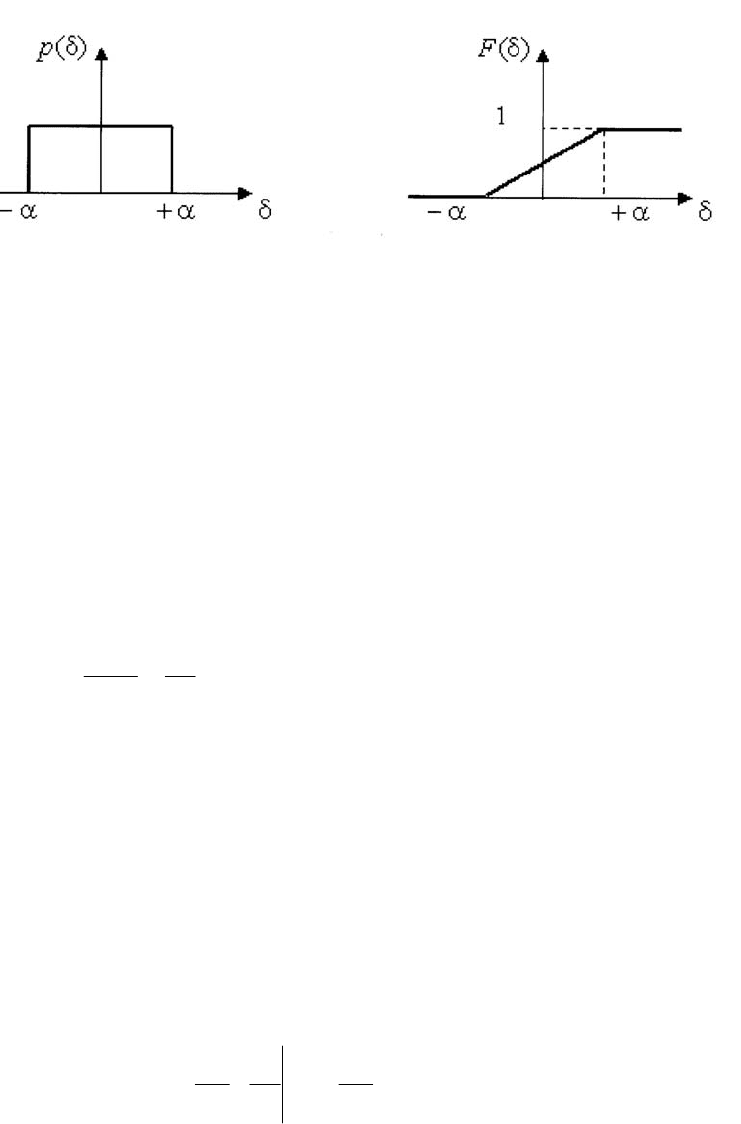
Такое распределение результатов наблюдений называется равномер-

ным.

Значения дифференциальной функции распределения равномерной

распределенной случайной погрешности постоянны в интервале [-

а; + а], а

вне этого интервала равны нулю (рисунок 1.4).

Рисунок 1.4 – Значения дифференциальной функции распределения равно-

мерной распределенной случайной погрешности

Поэтому выражение для дифференциальной функции распределения

случайной погрешности можно записать в виде























b,0

,ba,

,a,0

)(p

(1.34)

Определим числовые характеристики равномерного распределения.

Математическое ожидание случайной погрешности находим по формуле

(1.19):



























 0])([

d)(p][M

(1.35)