Коловский Ю В. Метрология, стандартизации и технические измерения

Подождите немного. Документ загружается.

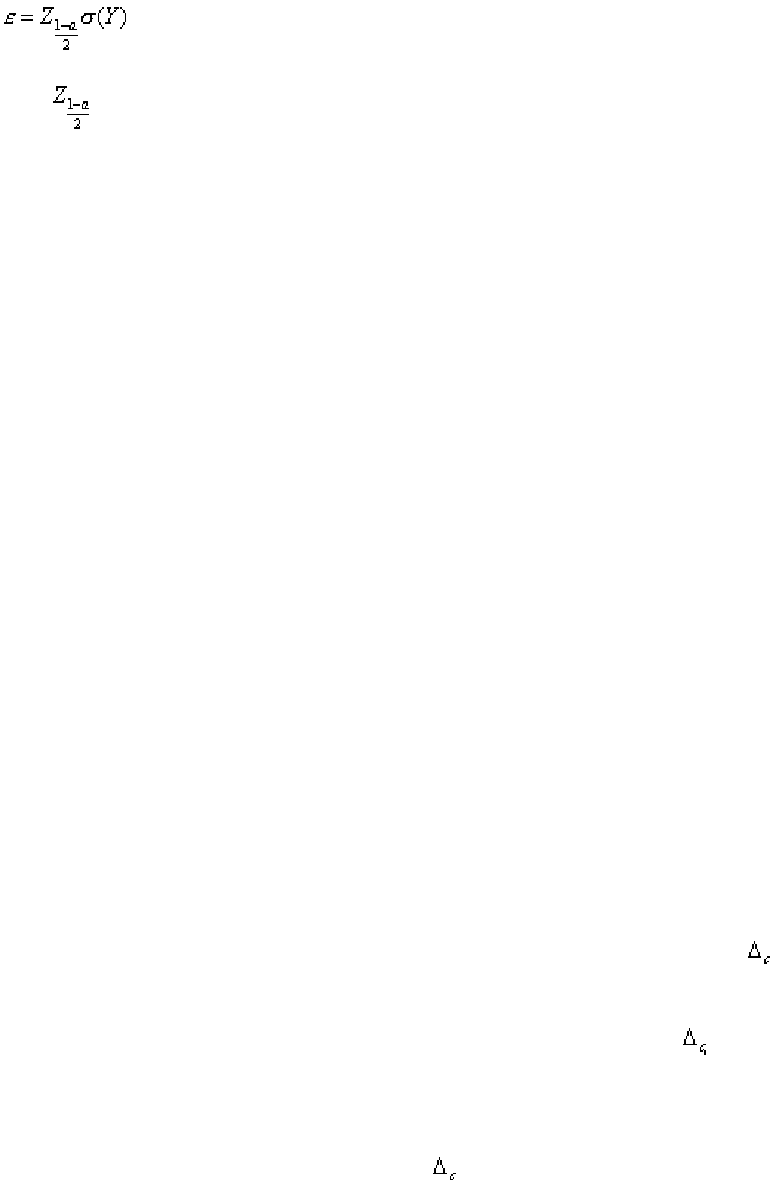
Если число наблюдений, выполненных при измерении всех параметров,

превышает 25 - 30, то доверительная граница случайной погрешности ре-

зультата косвенного измерения будет

(1.165)

где

- квантиль нормированного нормального распределения, соот-

ветствующая выбранной доверительной вероятности а.

Трудность возникает при меньшем числе наблюдений. В принципе при

этом можно использовать распределение Стьюдента, но неизвестно, как оп-

ределить число степеней свободы. Можно лишь утверждать, что оно должно

быть больше, чем число степеней свободы, отвечающее параметру, при изме-

рении которого

сделано минимальное число наблюдений. Точного решения

задача не имеет.

Обратимся к задаче оценивания систематических составляющих по-

грешности. Постоянные и найденные систематические погрешности измере-

ний параметров следует считать исключенными благодаря введению попра-

вок.

Вычисление доверительных границ неисключенной систематической

погрешности результата косвенных измерений

Неисключенными систематическими погрешностями могут быть по-

грешности метода, средств измерения

параметров, а также погрешности, вы-

званные другими источниками.

Реализации неисключенных систематических составляющих

будем

по совокупности возможных аналогичных измерений рассматривать как реа-

лизации случайной величины. Для каждой из составляющих

находят гра-

ницы возможных значений. При этом, принимая элементарные систематиче-

ские погрешности за случайные величины с равномерной плотностью рас-

пределения, получим, что распределение

изменяется в зависимости от чис-

ла слагаемых от равномерного до нормального. Соответственно этому для

вычисления границ неисключенной систематической погрешности результа-

та измерения целесообразно пользоваться разными формулами.

Если составляющие

общей погрешности считать распределенны-

ми в пределах своих границ

и поскольку всегда должно выполняться усло-

вие

(1.166)

то в качестве оценки границы результирующей неисключенной систе-

матической погрешности косвенных измерений следует принимать значение

рассчитанное в соответствии с условием:

(1.167)

где

- коэффициент, значения которого приведены в таблице 19.

Таблица 19

Число слагае-

мых n

Значение коэффициента

при довери-

тельной вероятности а

0,90 0,95 0,99 0,9973

2 0,97 1,10 1,27 1,34

3 0,96 1,12 1,37 1,50

4 * 1,12 1,41 1,58

5 * * 1,42 1,61

6 * * * 1,64

... ... ... ... ...

0,95 1,13 1,49 1,73

Примечание. Для граф таблицы, отмеченных *, коэффициент не вы-

числяется, т.к. q при данном n выходит за пределы крайнего интервала

В ряде случаев раздельная оценка систематической и случайной по-

грешностей результата исчерпывает задачу оценивания погрешности резуль-

тата измерения.

Однако часто необходимо найти общую погрешность измерения,

включающую в себя и случайную и систематическую составляющие.

Суммирование случайной и неисключенной систематической состав

ляющих общей погрешности косвенного измерения D при необходимости

выполняется с помощью формулы

(1.168)

Эта формула достаточно проста, но дает заведомо преувеличенную

оценку. Более правдоподобную оценку для D можно найти следующим пу-

тем: коэффициент

, определяющий соотношение между доверительной гра-

ницей и средним квадратическим отклонением случайной погрешности, оп-

ределяется распределением Стьюдента и известен. Имея оценки для q и

можно считать, что известен аналогичный коэффициент для систематической

погрешности

(1.169)

Искомый коэффициент

естественно считать какой-то функцией и

, отвечающей одной и той же вероятности. В качестве такой функции взято

среднее взвешенное значение, определяемое выражением:

(1.170)

Если по каким-либо причинам поправки к результатам измерений ар-

гументов нужно использовать для уточнения непосредственно результата

косвенного измерения, то в соответствии с формулой (88) для этого нужно

воспользоваться соотношением

(1.180)

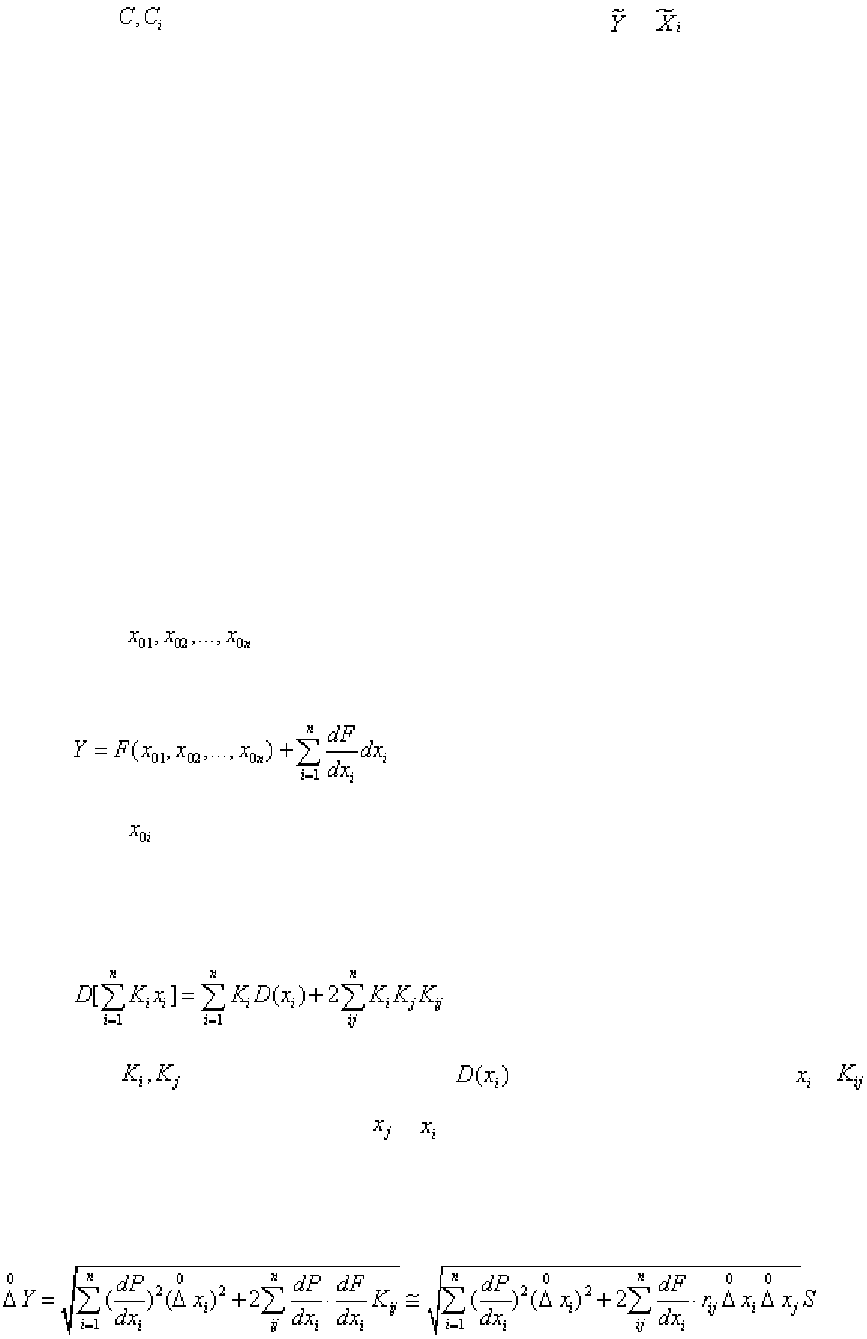
где - поправки к результатам измерений и .

Нелинейные косвенные измерения

Оценивание измеряемой величины подстановкой в формулу (88) оце-

нок параметров в общем случае допустимо только тогда, когда эта процедура

соответствует определению конкретной измеряемой величины за счет линей-

ного преобразования параметров. В других случаях возможность такого ре-

шения необходимо подтверждать. Исследование этого вопроса можно вы-

полнить на основе

разложения функции (86) в ряд Тейлора, обычно приме-

няемый для оценивания погрешностей косвенных нелинейных измерений.

Значение погрешности измерения всегда существенно меньше самой

измеряемой величины, следовательно, данная функция может быть с высокой

степенью точности представлена разложением в окрестности точки с коор-

динатами

в ряд Тейлора, в котором учтены члены только первой

степени:

(1.190)

где

- среднее арифметическое значение полученное в результате

прямых измерений.

Дисперсию суммы случайных величин записывают соотношением

(1.191)

где

- неслучайные числа; - дисперсия величины ; - кор-

реляционный момент величин

Пользуясь соотношением (95), запишем формулу для оценки случайной

погрешности косвенно измеряемой величины в следующем виде

(1.192)

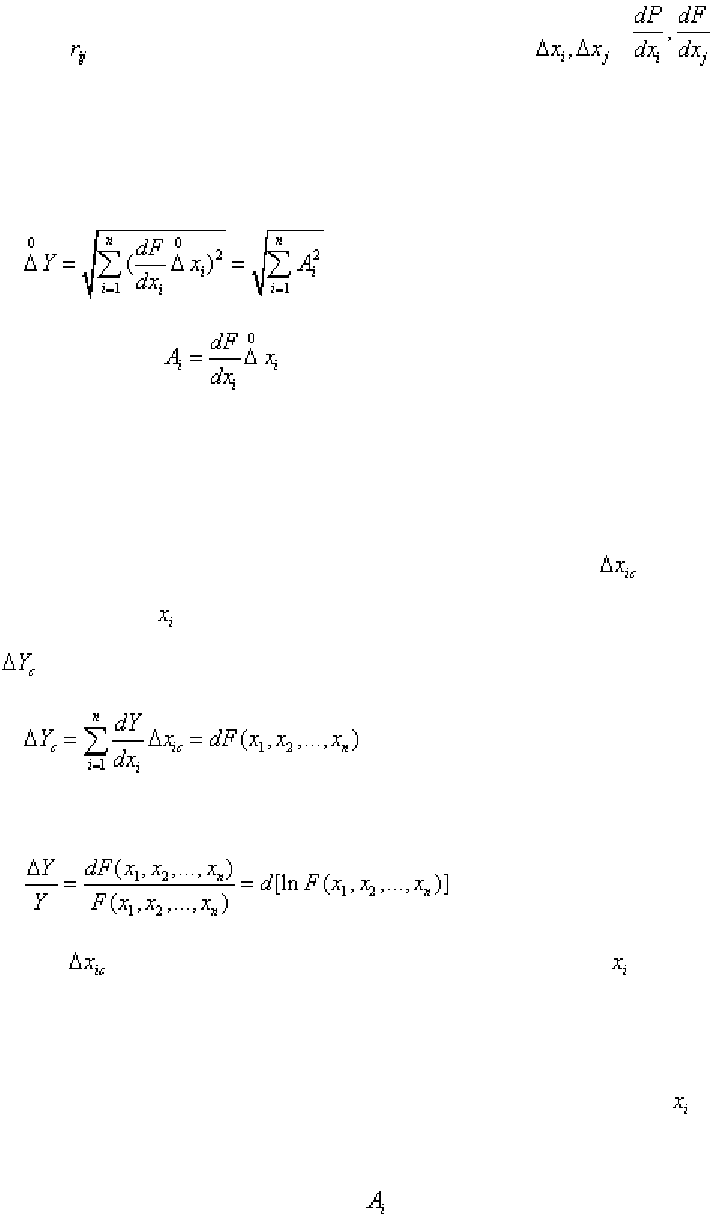
где - коэффициент корреляции величин ; - так называе-

мые коэффициенты влияния.

Если прямо измеряемые величины не коррелированы, то формула (96)

примет вид

(1.193)

Слагаемые

называют частными погрешностями косвенно из-

меряемой величины Y.

Формулы (97) и (98) употребляют в предположении, что систематиче-

ские погрешности устранены или учтены ранее каким-либо способом.

При наличии систематических погрешностей

в результатах изме-

ряемых величин

общую систематическую погрешность косвенного измере-

ния

вычисляют по формуле

(1.194)

или для относительной погрешности:

(1.195)

где

систематическая погрешность измерения .

Выведение рабочей формулы в соответствии с формулой (1.193) иногда

связано с громоздкими преобразованиями. Эти преобразования существенно

решаются для случаев, когда функция, связывающая Y и

, является лога-

рифмируемой.

Если частные погрешности

косвенно измеряемой величины Y не за-

висят одна от другой, то погрешность измерения DY является результатом

(функцией) действия частных погрешностей. Существуют следующие мето-

ды расчета погрешностей измерения: максимума-минимума, квадратичного

суммирования и вероятностный.

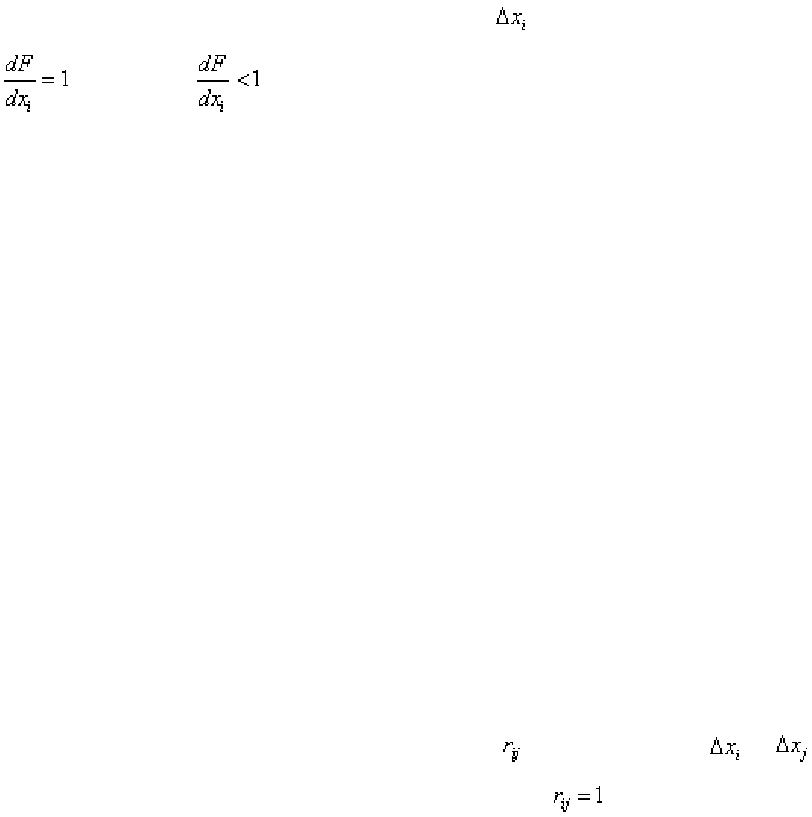
По методу максимума-минимума погрешность измерения находят

арифметическим суммированием предельных значений всех частных по-

грешностей - отдельно складывают все положительные и отдельно все отри-

цательные частные погрешности. Этот метод дает значительно завышенное

значение погрешности измерения DY. Применяется при расчете допусков.

По методу квадратичного сложения значения всех частных погрешно-

стей суммируются квадратично, т.е

. вычисляется корень квадратный из сум-

мы их квадратов. Данный метод дает относительно правильную оценку по-

грешности DY при некоррелированных

, если их коэффициенты влияния

. Обычно . Пренебрежение корреляционными связями может как

занижать, так и завышать значения погрешности DY. В общем случае, не

зная корреляционных связей, трудно судить о степени точности значения

средней квадратичной погрешности. Вместе с тем, в большинстве случаев

расчет по этому методу при наличии систематических погрешностей дает за-

вышенное значение погрешности измерения Y.

По вероятностному методу

осуществляют алгебраическое суммирова-

ние средних значений или математических ожиданий случайных и система-

тических погрешностей и квадратичное суммирование средних квадратиче-

ских значений случайных погрешностей. Вероятностный метод дает наибо-

лее точные результаты. При сложении большого числа частных погрешно-

стей, закон распределения которых отличается от нормального, закон рас-

пределения погрешности измерения, согласно центральной предельной

тео-

реме теории вероятностей, остается близким к нормальному при отсутствии

среди частных погрешностей доминирующей. Поэтому для оценки погреш-

ности измерения DY находят математическое ожидание M(DY) и ее диспер-

сию D(DY). Коэффициент корреляции

погрешностей и учитывает

тесноту зависимостей между ними. В случае

вероятностная зависимость

(97) переходит в функциональную.

Метод наименьших квадратов и общая схема его применения

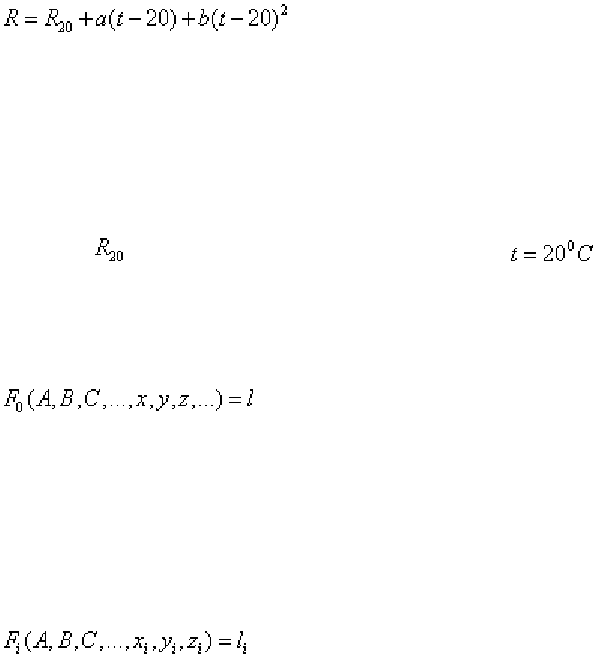
Совместные и совокупные измерения обычно выполняют так, что по-

лучаемое число уравнений, связывающих измеряемые величины, превышает

число последних. При этом из-за погрешностей измерений даже при точно

известной зависимости между величинами нельзя найти такие значения неиз-

вестных, при которых все уравнения выполнялись бы. В этих условиях зна-

чения неизвестных, принимаемые за

их оценки, находят с помощью метода

наименьших квадратов.

Примером совместных измерений может служить нахождение пара-

метров уравнения

(1.203)

выражающего температурную зависимость точного измерительного ре-

зистора (платинового термометра сопротивления).

Измеряя одновременно R - сопротивление резистора - и t - его темпера-

туру - и варьируя температуру, получаем несколько уравнений, из которых

нужно найти

- сопротивление резистора при - и температурные ко-

эффициенты a и b.

В общем виде можно написать, что имеем уравнение

(1.204)

где x, y, z, l - известные коэффициенты и непосредственно измеряемые

величины, A, B, C - искомые неизвестные.

Подставив полученные из опыта числовые значения x, y, z в уравнение

(101), получим ряд уравнений вида

(1.205)

которые содержат только неизвестные искомые величины A, B, C и чи-

словые коэффициенты.

Совместное решение полученных уравнений позволяет найти искомые

величины.

Пример совокупных измерений - нахождение емкости двух конденса-

торов по результатам измерений емкости каждого из них в отдельности, а

также при параллельном и последовательном их соединении. Каждое из этих

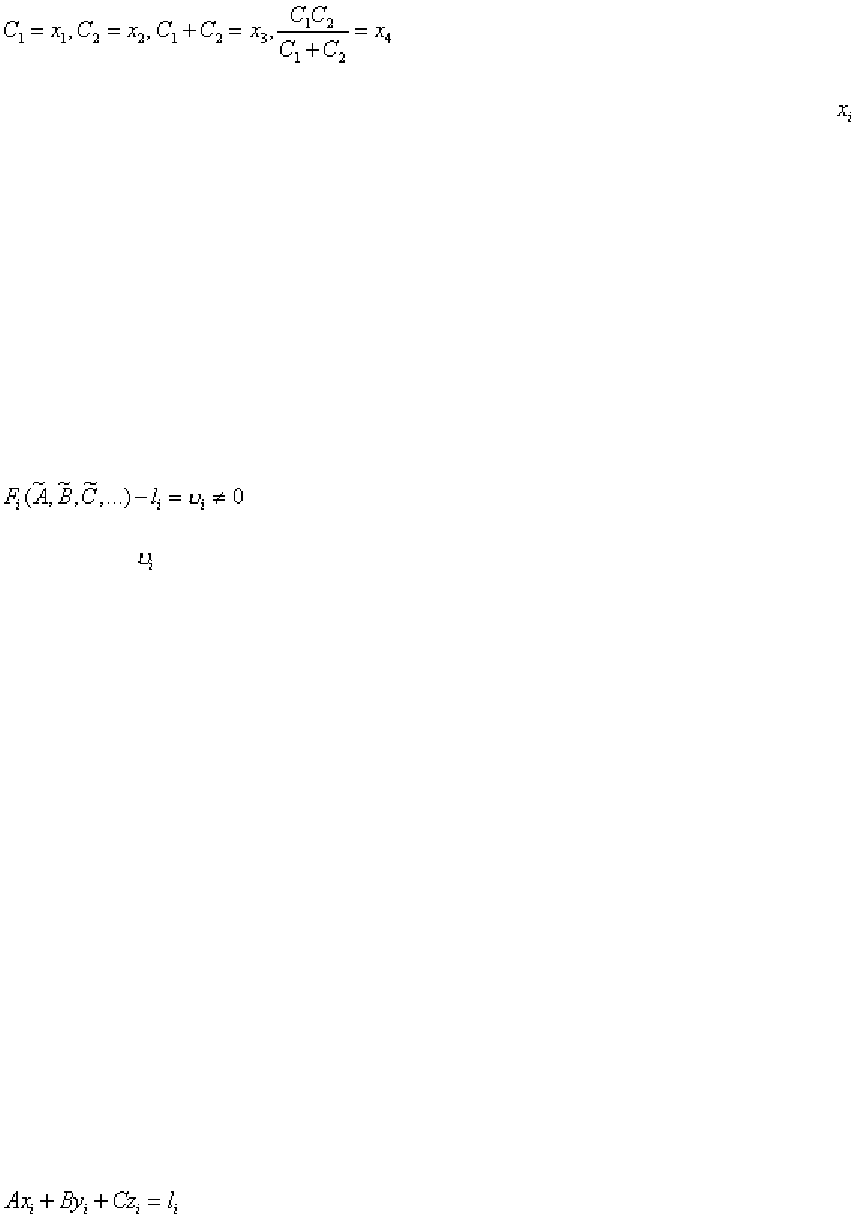
измерений выполняется с одним наблюдением, но в итоге для двух неизвест-

ных будем иметь четыре уравнения:

(1.206)

Подставив в эти уравнения экспериментально найденные значения

получим систему уравнений, аналогичную уравнениям (102).

Как уже отмечалось, обычно число уравнений системы (102) превыша-

ет число неизвестных и из-за погрешностей измерений нельзя найти такие

значения измеряемых величин, чтобы одновременно удовлетворились все

уравнения, даже если они сами по себе точно известны. Поэтому уравнения

(102) в отличие от обычных математических уравнений принято называть

условными. При подстановке в условные уравнения (102) найденных каким-

то путем значений неизвестных по отмеченным причинам получим:

(1.207)

Величины

принято называть невязкими. Всеобщее признание полу-

чило такое решение условных уравнений, которое приводит к минимуму

сумму квадратов невязок. Впервые этот принцип был сформулирован Ле-

жандром и называется принципом Лежандра; осуществляется этот принцип

методом, который получил наименование метода наименьших квадратов.

Методу наименьших квадратов и его применению при измерениях по-

священа обширная литература

. Теоретически показано, что при нормальном

распределении погрешностей метод наименьших квадратов приводит к оцен-

кам неизвестных, удовлетворяющим принципу максимума правдоподобия,

т.е. наиболее вероятным оценкам.

Мы остановимся на практическом применении метода наименьших

квадратов. Сначала рассмотрим применение метода для измерений, при ко-

торых условные уравнения являются линейными и точными. Для сокращения

записей

возьмем случай с тремя неизвестными.

Пусть система условных уравнений имеет вид

(1.208)

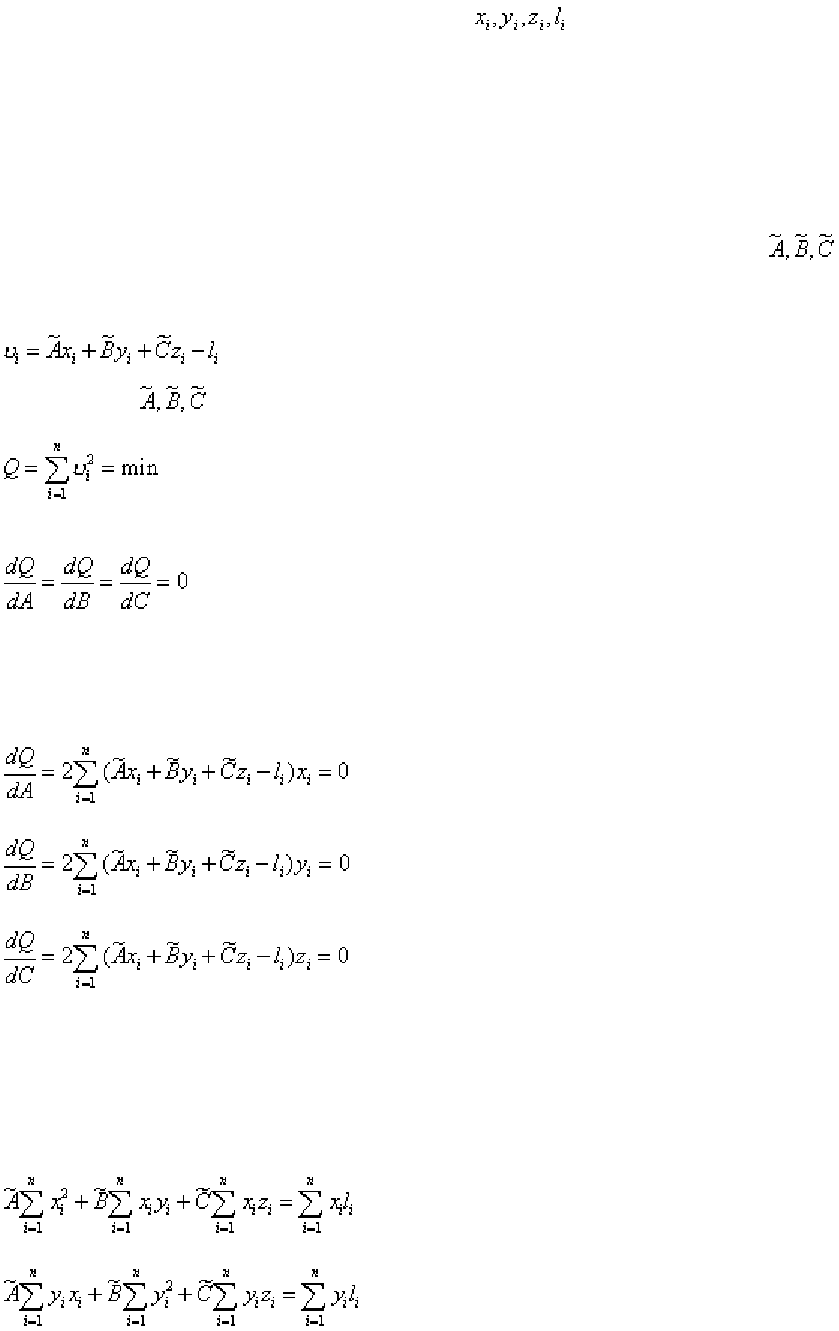
причем A,B,C - искомые неизвестные; - результаты i-го наблю-

дения и известные коэффициенты.

В общем случае число неизвестных m, причем m < n; если m = n, то

система условных уравнений решается однозначно, хотя получающиеся ре-

зультаты и отягощены погрешностями.

Если в (103) подставить какие-то оценки измеряемых величин

то

получим невязки

(1.209)

Найдем оценки из условия

(1.210)

Для выполнения этого условия необходимо, чтобы

(1.211)

Найдем эти частные производные и приравняем их к нулю:

(1.212)

(1.213)

(1.214)

Отсюда получаем систему так называемых нормальных уравнений:

(1.215)

(1.216)

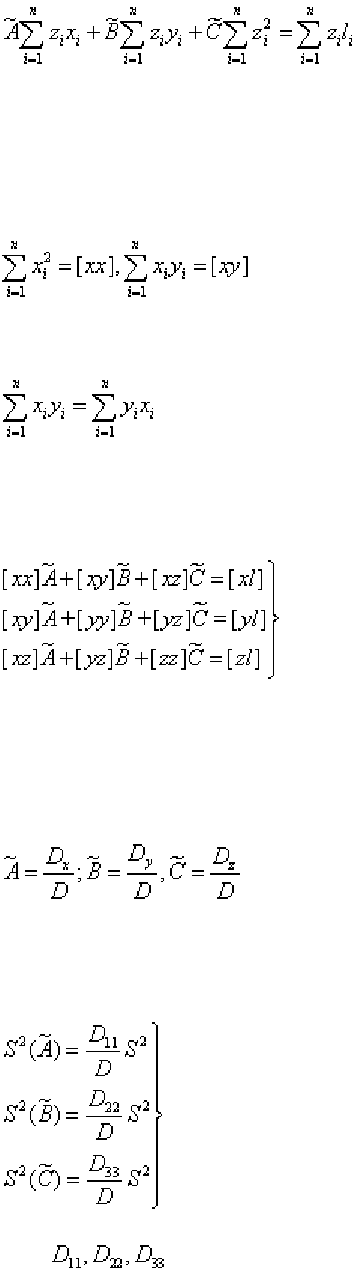
(1.217)

При написании нормальных уравнений часто пользуются обозначения-

ми Гаусса:

(1.218)

Очевидно, что

т.е. [xy]=[yx] (1.219)

В обозначениях Гаусса нормальные уравнения принимают более про-

стой вид:

(1.220)

Число нормальных уравнений равно числу неизвестных, и их решение

известными методами дает интересующие нас оценки измеряемых величин.

Наиболее кратко решение записывается с помощью определителей:

(1.221)

Оценки дисперсий найденных значений неизвестных можно вычис-

лить, пользуясь формулами:

(1.222)

где

- алгебраические дополнения элементов [xx], [yy], и [zz]

определителя D соответственно (они получаются путем удаления из матрицы