Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.


ψ
Σ
=0
ψ
k
ψ
k
ψ
d
ψ
Σ
ψ
Σ
=0



˙x
i
(t)=f
i
(x
1
,...,x
r
,y
r+1
,...,y
n
);
˙y
j
(t)=f
j
(x
1
,...,x
r
,y
r+1
,...,y
n
,u
1
,...,u
m
);
i =1, 2,...,r; j = r +1,r+2,...,n; m n − r.
u
1
,...,u
m

u
1
,...,u
m
u
1
,...,u
m
˙x(t)=λ
1
x − xy;
˙y(t)=−λ
2
y + x
2
+ u.
u =0
˙x(t)=λ
1
x − xy;
˙y(t)=−λ
2
y + x
2
,
u(x, y)
λ
2
>> |λ
1
|
˙y(t) ≈ 0
˙x(t)
∼
=
λ
1
x −
1
λ
2
x
3
,
x
y
x
2
− λy
∼
=
0.
λ
1c
=0 λ
1
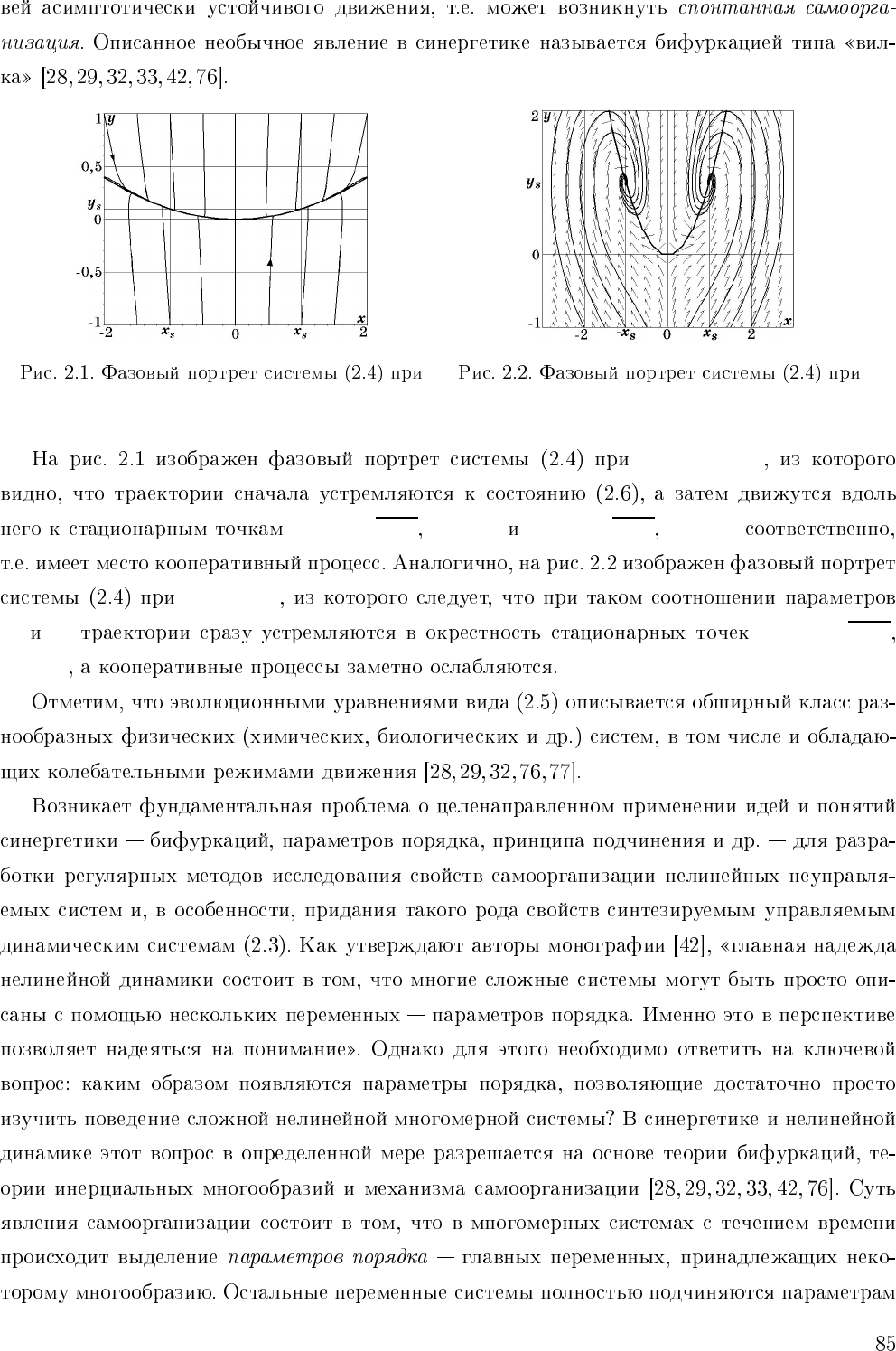
λ
2
/λ
1
= 100 λ
2
/λ
1
=1
λ
2
/λ
1
= 100
x
s
=+
√
λ
1
λ
2
y
s
= λ
1
x
s
= −
√
λ
1
λ
2
y
s
= λ
1
λ
2
/λ
1
=1
λ
1
λ
2
x
s
= ±
√
λ
1
λ
2
y
s
= λ
1

˙
x(t)=F(x),
x(x
1
,x
2
,...,x
n
) x
1
,x
2
,...,x
n
z(t) η v(t)
˙
z(t)=F
1
(z, v);
˙
v(t)=F
2
(z, v).
v = Φ(z)
d
dt
Φ(z) − F
2
(z, v) ≡ 0.
n
η
˙
z(t)=F
1
(z, Φ(z))
n − η
z
z(t)
v(t)
z(t)
x(t)

x
i
(t)
x
i
(t)

ψ
1
(x, y)=x
2
− λ
2
y.
ψ
1
(x, y)=0
T
1
˙
ψ
1
(t)+ψ
1
=0.
ψ
1
(x, y)
u
1
u
1
=
2λ
1
λ
2
− 1
x
2
−
2
λ
2
x
2
y + λ
2
y +
1
λ
2
T
1
ψ
1
.
u
1
˙x(t)=λ
1
x − xy;
˙y(t)=
2λ
1
λ
2
x
2
−
2
λ
2
x
2
y +
1
λ
2
T
1
ψ
1
.
ψ
1
=0
dt
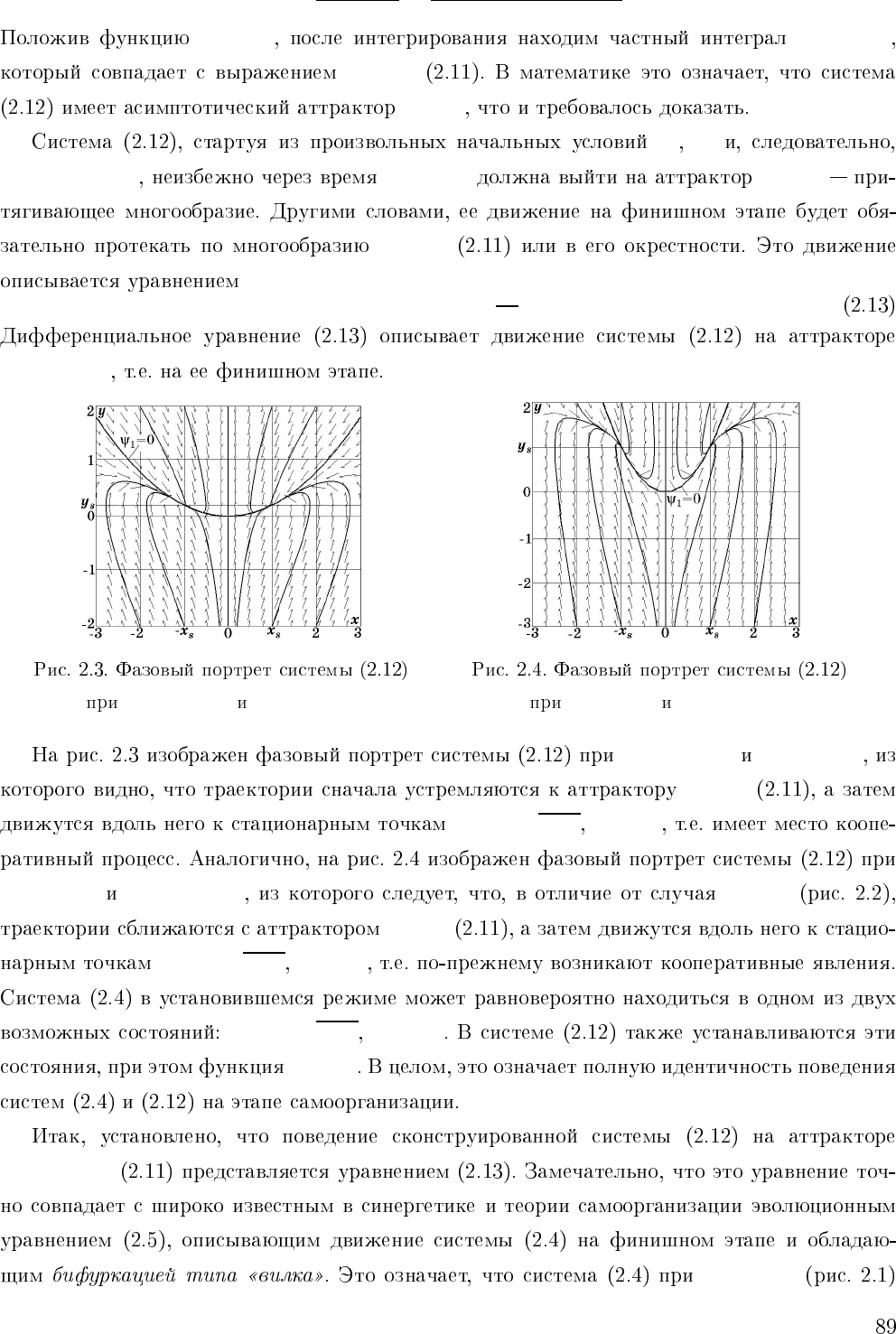
dt =
dx
λ
1
x − xy
=
λ
2
T
1
dy
2T
1
(λ
1
x − xy)x + ψ
1
.
ψ
1
=0 x
2
= λ
2
y
ψ
1
=0
ψ
1
=0
x
0
y
0
ψ
0
= x
2
0
− λ
2
y
0
(4 ÷ 5)T
1
ψ
1
=0
ψ
1
=0
˙x
ψ
(t)=λ
1
x
ψ
−
1
λ
2
x
3
ψ
.
ψ
1
(x, y)=0
λ
2
/λ
1
= 100 T
1
=10/λ
2
λ
2
/λ
1
=1 T
1
=0, 5/λ
2
λ
2
/λ
1
= 100 T
1
=10/λ
2
ψ
1
=0
x
s
= ±
√
λ
1
λ
2
y
s
= λ
1
λ
2
/λ
1
=1 T
1
=0, 5/λ
2
u
1
=0
ψ
1
=0
x
s
= ±
√
λ
1
λ
2
y
s
= λ
1
x
s
= ±
√
λ
1
λ
2
y
s
= λ
1
u
1s
=0
ψ
1
(x, y)=0
λ
2
|λ
1
|
