Кочергин В.И. Теория многомерных цифро-векторных множеств
Подождите немного. Документ загружается.

Глава 5
320
*
и
x′
1
*
x
1
и и и и
a
1
a
2
a
3
a
4
*
*
*
*
*
*
*
*
*
*
* *
a
5
a
8
x
1
a
11
x
3
* *
* *
и
1
* *
(a
5
)
x
2
x
4
*
*
3
* *
a
6
a
8
x
1
a
11
x
3
* *
* *
и
и
(a
6
)
2
* *
* *
a
9
a
7
a
8
x
3
x
4
* *
* *
и
и
(a
9
)
4
* *
x
2
a
10
(a
10
)
a
7
a
8
a
11
* *
* *
и
и
5
x
2
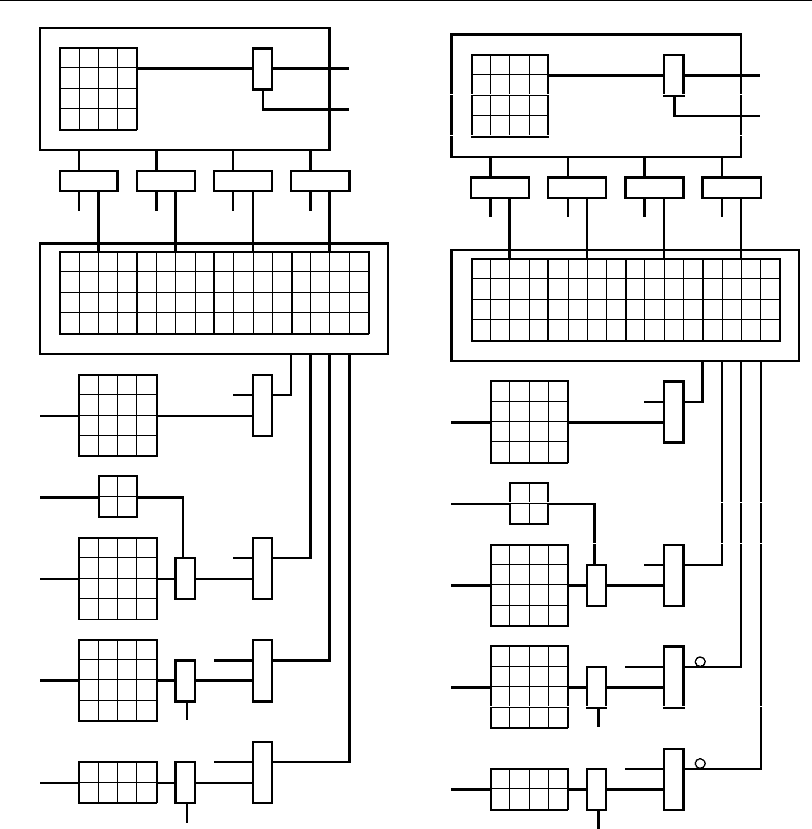
Рис. 5.35 Рис. 5.36
Выберем в качестве базового геометрического образа в координатах про-
странства a
1
– a
4
такой же образ, какой был принят нами для информационных
разрядов a
5
– a
11
. Этот образ соответствует функции 0… (см. рис. 5.14). Тогда,
аналогично описанной выше процедуре построения функциональных схем ис-
правления ошибок информационной части систематического кода, могут быть
синтезированы функциональные схемы его контрольной части.
Эти функциональные схемы для разрядов x
1
– x
4
приведены соответствен-
но на рис. 5.35 – 5.38. Все схемы этих рисунков содержат одинаковые блоки
базового геометрического образа БГО (a
1
– a
4
), которые управляются последо-
вательно соединенными блоками поворота координат БП (a
7
a
8
a
11
; x
1
– x
4
) и
БП (a
1
– a
4
).
*
и
x′
2
*
x
2
и и и и
a
1
a
2
a
3
a
4
* *
*
*
*
*
*
*
*
*
* *
a
5
a
8
x
1
a
11
x
3
* *
* *
и
1
* *
(a
5
)
x
2
x
4
*
*
3
* *
a
6
a
8
x
1
a
11
x
3
* *
* *
и
и
(a
6
)
2
* *
* *
a
9
a
7
a
8
x
3
x
4
* *
* *
и
и
(a
9
)
4
* *
x
2
a
10
(a
10
)
a
7
a
8
a
11
* *
* *
и
и
5
x
2

Систематический код с исправлением одиночных ошибок
321
*
и
x′
3
*
x
3
и и и и
a
1
a
2
a
3
a
4
*
*
*
*
*
*
*
*
*
*
* *
a
5
a
8
x
1
a
11
x
3
* *
* *
и
1
* *
(a
5
)
x
2
x
4
*
*
3
* *
a
6
a
8
x
1
a
11
x
3
* *
* *
и
и
(a
6
)
2
* *
* *
a
9
a
7
a
8
x
3
x
4
* *
* *
и
и
(a
9
)
4
* *
x
2
a
10
(a
10
)
a
7
a
8
a
11
* *
* *
и
и
5
x
2
Рис. 5.37 Рис. 5.38
Функциональные схемы БП (a
1
– a
4
) в каждом из контрольных разрядов
x
1
– x
4
одинаковые, а схемы БП (a
5
a
6
a
9
a
10
) отличаются незначительно только
инверсиями выходных сигналов (a
5
),
(a
6
),
(a
9
),
(a
10
)
и содержат одинаковые
функциональные схемы, нумерация которых совпадает с аналогичным блоком
информационной части кода сигналов a
1
– a
4
.
Общее число функциональных схем в устройстве, исправляющем оди-
ночные ошибки всего систематического кода, равно 21.
Функционально все схемы этих блоков однотипны и отличаются одна от
другой только числом входов и порядком подаваемых на эти входы сигналов
разрядов систематического кода a
7
,
a
8
,
a
11
; x
1
– x
4
.
*
и
x′
4
*
x
4
и и и и
a
1
a
2
a
3
a
4
* *
*
*
*
*
*
*
*
*
* *
a
5
a
8
x
1
a
11
x
3
* *
* *
и
1
* *
(a
5
)
x
2
x
4
*
*
3
* *
a
6
a
8
x
1
a
11
x
3
* *
* *
и
и
(a
6
)
2
* *
* *
a
9
a
7
a
8
x
3
x
4
* *
* *
и
и
(a
9
)
4
* *
x
2
a
10
(a
10
)
a
7
a
8
a
11
* *
* *
и
и
5
x
2
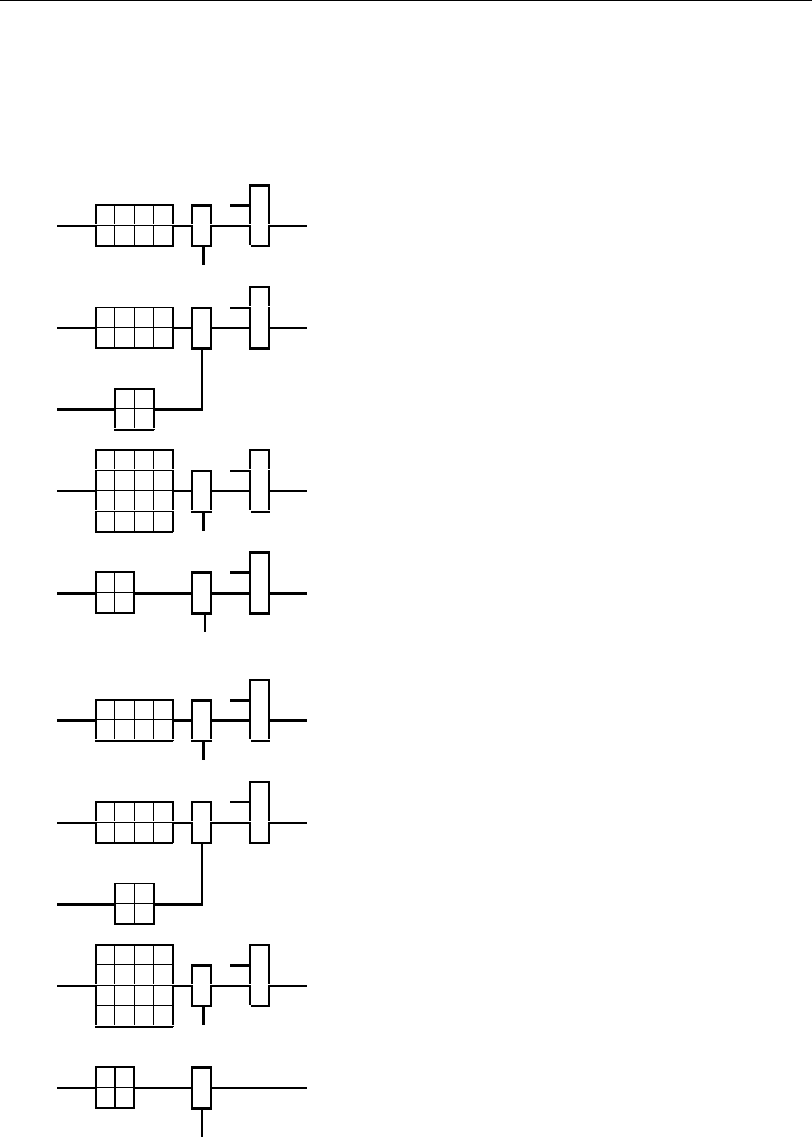
Глава 5
322
Представляет определенный практический интерес рассмотреть измене-
ние функциональных схем исправления одиночных ошибок во всех разрядах
систематического кода, когда число его информационных разрядов уменьша-
ется от 11 до 5. Синтезируемые таким образом новые систематические коды,
когда число контрольных разрядов остается неизменным, сохраняют возмож-
ность исправления всех одиночных ошибок в
информационной и контрольной его части, но
использование цифрового пространства коор-
динат при этом уменьшается, т.е. в этом циф-
ровом пространстве будут появляться ячейки,
не заполненные одиночными ошибками.
Это изменение функциональных схем ка-
сается только одного блока поворота коорди-
нат БП (a
5
a
6
a
9
a
10
), а все остальные блоки ос-
таются неизменными (см. рис. 5.12, 5.16 –
5.28, 5.35 – 5.38). Если цифровое пространство,
где все ячейки заполняются штатными цифра-
ми и их одиночными ошибками, является со-
вершенным, то новое видоизмененное контро-
лируемое пространство будет квазисовершен-
ным.
В качестве примера синтеза таких квази-
совершенных кодов рассмотрим последова-
тельное уменьшение информационных разря-
дов первичного совершенного кода и просле-
дим изменение блоков БП (a
5
a
6
a
9
a
10
) только
для первых четырех его информационных раз-
рядов (см. рис. 5.12), для которых этот блок
общий. При этом, исходя из наглядности пре-
образований, не будем стремиться уменьшать
уровень схем этого блока, т.е. стремиться по-
высить их быстродействие, хотя при таких уп-
рощениях это целесообразно выполнять.
Изменение этих блоков в других инфор-
мационных и контрольных разрядах кода при
таком геометрическом синтезе не представляет
какой-либо сложности и может быть выполне-
но читателем самостоятельно.
Все последовательные преобразования
блока БП (a
5
a
6
a
9
a
10
) при этих синтезах приве-
дены на рис. 5.39, а – е, что сопровождается
соответствующим изменением функциональ-
ных схем 1 – 5.
a
5
a
8
x
1
x
4
**
(a
5
)
**
и
и
1
x
2
a
6
a
8
x
1
x
3
**
(a
6
)
**
и
и
2
x
2
x
4
*
*
3
**
a
9
a
7
a
8
x
3
x
4
**
(a
9
)
**
и
и
4
**
x
2
a
10
a
7
a
8
5
*
(a
10
)
*
и
и
a
11
= 0* x
2
а)
a
5
a
8
x
1
x
4
**
(a
5
)
**
и
и
1
x
2
a
6
a
8
x
1
x
3
**
(a
6
)
**
и
и
2
x
2
x
4
*
*
3
**
a
9
a
7
a
8
x
3
x
4
**
(a
9
)
**
и
и
4
**
x
2
a
7
a
8
5
*
(a
10
)
*
и
a
10
= a
11
= 0*
x
2
б)
Рис. 5.39 (начало)
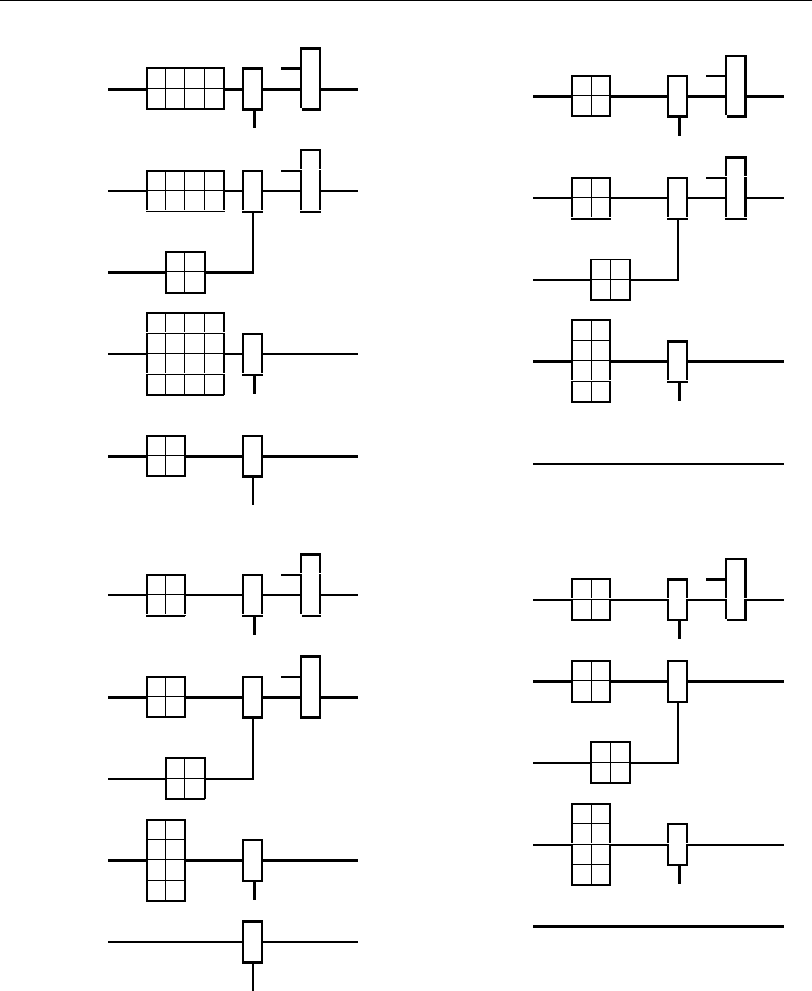
Систематический код с исправлением одиночных ошибок
323
Рис. 5.39 (продолжение)
В заключение синтеза необходимо отметить следующее: все функцио-
нальные схемы блоков БП (a
5
a
6
a
9
a
10
), а также схемы шифраторов обладают
определенным видом симметрии. Это свидетельствует о том, что при выпол-
нении мысленных поворотов относительно осей симметрии пространства,
a
5
a
8
x
1
x
4
**
(a
5
)
**
и
и
1
x
2
a
6
a
8
x
1
x
3
**
(a
6
)
**
и
и
2
x
2
x
4
*
*
3
**
a
7
a
8
x
3
x
4
**
(a
9
)
**
и
4
**
x
2
a
7
a
8
5
*
(a
10
)
*
и
a
9
= a
10
= a
11
=0*
x
2
в)
a
5
x
1
x
4
*
(a
5
)
*
и
и
1
x
2
a
6
x
1
x
3
*
(a
6
)
*
и
и
2
x
2
x
4
*
*
3
*
a
7
x
3
x
4
*
(a
9
)
*
и
4
*
x
2
a
7
5
(a
10
)
и
a
8
=a
9
= a
10
= a
11
=0*
x
2
г
)
a
5
x
1
x
4
*
(a
5
)
*
и
и
1
x
2
a
6
x
1
x
3
*
(a
6
)
*
и
и
2
x
2
x
4
*
*
3
*
x
3
x
4
*
(a
9
)
*
и
4
*
x
2
x
2
5
(a
10
)
a
7
=a
8
= a
9
= a
10
= a
11
= 0*
д)
a
5
x
1
x
4
*
(a
5
)
*
и
и
1
x
2
x
1
x
3
*
(a
6
)
*
и
2
x
2
x
4
*
*
3
*
x
3
x
4
*
(a
9
)
*
и
4
*
x
2
x
2
5
(a
10
)
a
6
=a
7
=a
8
= a
9
= a
10
=a
11
= 0*
е)
Глава 5
324
совпадающих с осями симметрии геометрических образов, последние остают-
ся неизменными. Следовательно, существует некоторое определенное число
эквивалентных схем, которые отличаются одна от другой только ансамблями
их входных сигналов.
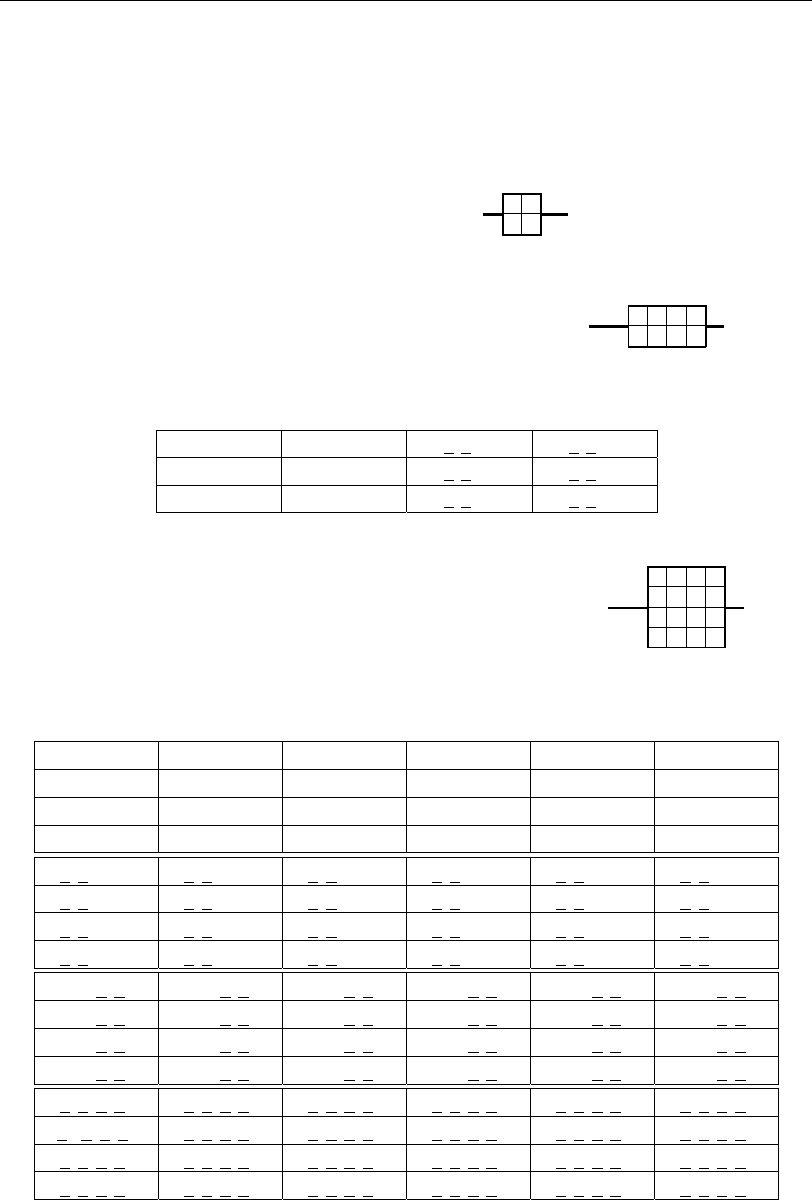
Во всех этих схемах используются три геометрических образа, на кото-
рых необходимо остановиться.
Это прежде всего схема инвертора
(исключающее ИЛИ ) и не требует дополнительных пояснений.
Вторым является образ трехвходовой функции
число таких ансамблей входа определяется табл. 5.3.1.
Таблица 5.3.1
z
1
z
2
z
3
z
1
z
3
z
2
z
1
z
2
z
3
z
1
z
3
z
2
z
2
z
1
z
3
z
2
z
3
z
1
z
2
z
1
z
3
z
2
z
3
z
1
z
3
z
2
z
1
z
3
z
1
z
2
z
3
z
2
z
1
z
3
z
1
z
2
Третьим будет образ четырехвходовой функции
табл. 5.3.2 определяет для нее аналогичные значения входных сигналов.
Таблица 5.3.2
z
4
z
5
z
6
z
7
z
4
z
6
z
5
z
7
z
4
z
7
z
6
z
5
z
4
z
5
z
7
z
6
z
4
z
6
z
7
z
5
z
4
z
7
z
5
z
6
z
5
z
4
z
6
z
7
z
5
z
6
z
4
z
7
z
5
z
7
z
6
z
4
z
5
z
4
z
7
z
6
z
5
z
6
z
7
z
4
z
5
z
7
z
4
z
6
z
6
z
5
z
4
z
7
z
6
z
4
z
5
z
7
z
6
z
7
z
4
z
5
z
5
z
6
z
7
z
4
z
6
z
4
z
7
z
5
z
6
z
7
z
5
z
4
z
7
z
6
z
5
z
4
z
7
z
5
z
6
z
4
z
7
z
4
z
5
z
6
z
7
z
6
z
4
z
5
z
7
z
5
z
4
z
6
z
7
z
4
z
6
z
5
z
4
z
5
z
6
z
7
z
4
z
6
z
5
z
7
z
4
z
7
z
6
z
5
z
4
z
5
z
7
z
6
z
4
z
6
z
7
z
5
z
4
z
7
z
5
z
6
z
5
z
4
z
6
z
7
z
5
z
6
z
4
z
7
z
5
z
7
z
6
z
4
z
5
z
4
z
7
z
6
z
5
z
6
z
7
z
4
z
5
z
7
z
4
z
6
z
6
z
5
z
4
z
7
z
6
z
4
z
5
z
7
z
6
z
7
z
4
z
5
z
5
z
6
z
7
z
4
z
6
z
4
z
7
z
5
z
6
z
7
z
5
z
4
z
7
z
6
z
5
z
4
z
7
z
5
z
6
z
4
z
7
z
4
z
5
z
6
z
7
z
6
z
4
z
5
z
7
z
5
z
4
z
6
z
7
z
4
z
6
z
5
z
4
z
5
z
6
z
7
z
4
z
6
z
5
z
7
z
4
z
7
z
6
z
5
z
4
z
5
z
7
z
6
z
4
z
6
z
7
z
5
z
4
z
7
z
5
z
6
z
5
z
4
z
6
z
7
z
5
z
6
z
4
z
7
z
5
z
7
z
6
z
4
z
5
z
4
z
7
z
6
z
5
z
6
z
7
z
4
z
5
z
7
z
4
z
6
z
6
z
5
z
4
z
7
z
6
z
4
z
5
z
7
z
6
z
7
z
4
z
5
z
5
z
6
z
7
z
4
z
6
z
4
z
7
z
5
z
6
z
7
z
5
z
4
z
7
z
6
z
5
z
4
z
7
z
5
z
6
z
4
z
7
z
4
z
5
z
6
z
7
z
6
z
4
z
5
z
7
z
5
z
4
z
6
z
7
z
4
z
6
z
5
z
4
z
5
z
6
z
7
z
4
z
6
z
5
z
7
z
4
z
7
z
6
z
5
z
4
z
5
z
7
z
6
z
4
z
6
z
7
z
5
z
4
z
7
z
5
z
6
z
5
z
4
z
6
z
7
z
5
z
6
z
4
z
7
z
5
z
7
z
6
z
4
z
5
z
4
z
7
z
6
z
5
z
6
z
7
z
4
z
5
z
7
z
4
z
6
z
6
z
5
z
4
z
7
z
6
z
4
z
5
z
7
z
6
z
7
z
4
z
5
z
5
z
6
z
7
z
4
z
6
z
4
z
7
z
5
z
6
z
7
z
5
z
4
z
7
z
6
z
5
z
4
z
7
z
5
z
6
z
4
z
7
z
4
z
5
z
6
z
7
z
6
z
4
z
5
z
7
z
5
z
4
z
6
z
7
z
4
z
6
z
5
*
f
m
1
m
2
*
, которая общеизвестна
z
1
z
2
z
3
**
f
**
, где
**
z
4
z
5
z
6
z
7
**
f
**
**
, где

Систематический код с исправлением одиночных ошибок
325
Здесь нумерация сигналов на этих двух функциональных схемах принята
условно сквозной z
1
– z
7
.
В каждой функциональной схеме блоков БП (a
5
a
6
a
9
a
10
) на входе могут
быть поданы ансамбли сигналов в соответствии с этими таблицами, что опре-
деляет огромное количество эквивалентных схем исправления ошибок систе-
матического кода.
5.4. Структурная схема исправления ошибок во
всех разрядах систематического кода
Простота и наглядность представленного выше геометрического синтеза
очевидны и не требуют дополнительных пояснений.
Однако следует провести некоторый критический разбор представленного
варианта синтеза, где определенным достижением является то, что одна и та
же схема блока БП (a
5
a
6
a
9
a
10
) используется в устройствах исправления оши-
бок в информационных (a
1
– a
4
) и контрольных (x
1
– x
4
)
разрядах, где для каж-
дого из разрядов меняются только сочетание прямых и инверсных сигналов на
выходе этого блока. Причем в контрольных разрядах для реализации покрытия
функций исправления одиночных ошибок применяется один общий базовый
геометрический образ функции в координатах пространства a
5
a
6
a
9
a
10
.
Отличие же устройств исправления ошибок в информационных разрядах
a
5
– a
11
заключается в том, что в каждом из них использовался свой базовый
геометрический образ в координатах пространства a
5
a
6
a
9
a
10
, который распо-
лагался в начале координат общего цифрового пространства систематического
кода. Это обстоятельство привело к значительному усложнению всей схемы
устройства исправления ошибок, которая связана с необходимостью иметь
различные блоки БП (a
5
a
6
a
9
a
10
) в каждом информационном разряде a
5
– a
11
.
Несмотря на то, что базовые геометрические образы функций в координа-
тах a
5
a
6
a
9
a
10
для информационных (a
1
– a
4
) и контрольных (x
1
– x
4
) разрядов
различны, они имеют одинаковую структуру построения, которая определяет-
ся одинаковым расположением составляющих их функций (m
1
↔ 5… , m
2
↔
0… , m
3
↔ 7… , m
4
↔ 2… , m
5
↔4… , m
6
↔1… , m
7
↔6… , m
8
↔3… ,) в этих
координатах базового геометрического образа. Именно это позволяет иметь
один блок БП (a
5
a
6
a
9
a
10
) для информационных (a
1
– a
4
) и контрольных (x
1
– x
4
)
разрядов.
Учитывая это обстоятельство, используем одинаковый базовый геометри-
ческий образ, который был выбран для контрольных разрядов (см. рис. 5.34),
для информационных разрядов (a
1
– a
4
) систематического кода. Тогда, выпол-
няя все перечисленные выше правила построения геометрических образов ис-
правленных сигналов a′
1
– a′
11
, получим один блок БП (a
5
a
6
a
9
a
10
) для всех ин-
формационных и контрольных разрядов этого кода, где для каждого из разря-
дов меняются только сочетание прямых и инверсных сигналов на входных
шинах этого блока.
Глава 5
326
Выходные сигналы этого блока, которые поступают на входные шины со-
ответствующих блоков БП(a
1
– a
4
), задаются данными табл. 5.4.1.
Таблица 5.4.1
Сигналы блока БП(a
5
a
6
a
9
a
10
)
Разряды
(a
5
)(a
5
) (a
6
)(a
6
) (a
9
)(a
9
) (a
10
) (a
10
)
a
1
– a
4
*
* * *
a
5
* * * *
a
6
* * * *
a
7
* * * *
a
8
* * * *
a
9
* * * *
a
10
* * * *
a
11
* * * *
x
1
* * * *
x
2
* * * *
x
3
* * * *
x
4
* * * *
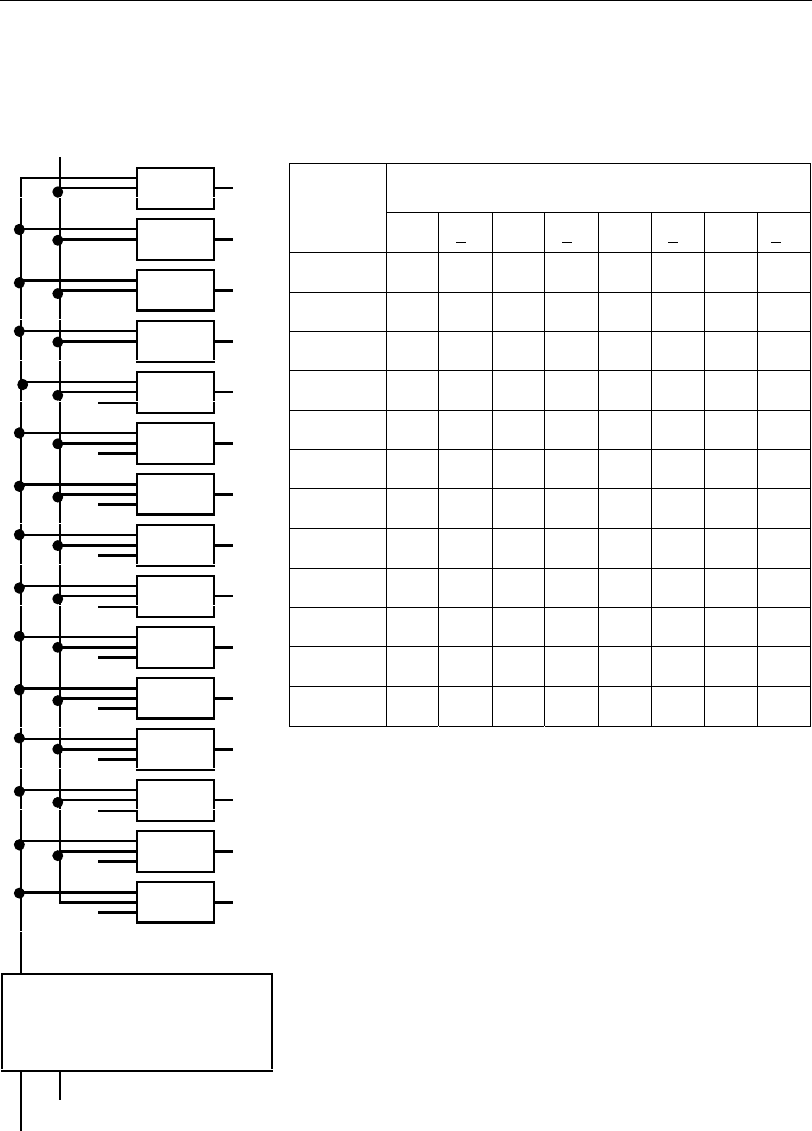
Синтезированная таким образом структурная
схема устройства исправления одиночных оши-
бок (рис. 5.40) содержит общий функциональный
блок поворота координат БП (a
5
a
6
a
9
a
10
), прямые и
инверсные сигналы (a
5
), (a
6
), (a
9
), (a
10
) которого
поступают на первые входные шины блоков
БГО1 – БГО5. На вторые входные шины этих бло-
ков подаются сигналы a
1
– a
4
первых четырех ин-
формационных разрядов. Блоки БГО1 – БГО4
формируют соответственно исправленные сигна-
лы a′
1
– a′
4
, а одиннадцать блоков БГО5 формиру-
ют аналогичные сигналы a′
5
– a′
11
; x′
1
– x′
4
, где в
каждом из этих блоков имеется третий вход, на
который поступают соответствующие этому блоку
сигналы a
5
– a
11
; x
1
– x
4
.
a
1
– a
4
БГО1
a′
1
БГО2
a′
2
БГО3
a′
3
БГО4
a′
4
БГО5
a′
5
a
5
БГО5
a′
6
a
6
БГО5
a′
7
a
7
БГО5
a′
8
a
8
БГО5
a′
9
a
9
БГО1
a′
10
a
10
БГО5
a′
11
a
11
БГО5
x′
1
x
1
БГО5
x′
2
x
2
БГО5
x′
3
x
3
БГО5
x′
4
x
4
(a
5
), (a
6
), (a
9
), (a
10
)
БП (a
5
a
6
a
9
a
10
),
a
5
,
a
6
,
a
9
,
a
10
a
7
,
a
8
,
a
11
; x
1
– x
4
Рис. 5.40

Систематический код с исправлением одиночных ошибок
327
При уменьшении числа информационных разрядов кода происходит ис-
чезновение соответствующих им блоков БГО5, а также изменяется общий
блок БП (a
5
a
6
a
9
a
10
), как это представлено выше на функциональных схемах
рис. 5.39, а – е.
Функциональная схема БП (a
5
a
6
a
9
a
10
) состоит из трех четырехвходовых
функций, геометрический образ которых обладает полной симметрией относи-
тельно осей двухмерного пространства, и одной трехвходовой функцией,
имеющей ограниченную симметрию в этой мерности пространства. Учитывая
это обстоятельство, в соответствии с данными табл. 5.3.1, 5.3.2 общее число
эквивалентных схем этого блока равно 10616832, в каждой из которых меня-
ются только местами либо одновременно инвертируются сигналы на входных
шинах составляющих их схем.
Математиков не должен смущать
практический подход, ибо решение практи-
ческих задач часто приводит к глубокому
исследованию «абстрактных» математиче-
ских объектов.
Э. Берлекэмп
Есть одна опасность в обращении к
классическим работам, кажется, что на
них все ссылаются, но редко кто их читает.
Г. Глинский
Глава 6
ПРОДОЛЖЕНИЕ ГЕОМЕТРИЧЕСКОГО СИНТЕЗА
КОДОВ, ИСПРАВЛЯЮЩИХ ОШИБКИ
История исследования систематических совершенных кодов с информаци-
онной частью основания n = 2
4
начинается с работы математика Р. Фишера
(1942) [1], где представлен один из этих кодов. Аналогичный код этого основа-
ния был в качестве примера приведен в работе К. Шеннона (1948) [3] и в даль-
нейшем был обобщен М. Голеем (1949) [4]. Однако в литературе эти коды
обычно связывают с именем Р. Хемминга (1950), который в [5] представил не-
которое число этих кодов, позволяющих как обнаружить, так и исправить неко-
торые типы ошибок. Историческая неточность такого представления совершен-
ных кодов однозначно отмечается в книге Э. Берлекэмпа [6], внесшего сущест-
венный вклад в теорию кодов, исправляющих ошибки.
К совершенным систематическим кодам, исправляющим определенные
группы ошибок (одиночные; одиночные и двойные; одиночные, двойные и
тройные и т.д.), необходимо отнести также мажоритарный код для основания n
= 2, который представлен в работе Дж. фон Неймана (1952) [2]. Совершенные
коды этого основания содержат один информационный разряд и определенное
количество контрольных разрядов, совпадающих с информационным. Число
этих контрольных разрядов равно 2, 4, 6, …, что гарантирует кодовое расстоя-
ние между цифрами 0 и 1, – соответственно 3, 5, 7, … . Эти числа и определяют
минимальное кодовое расстояние, которое должно быть между штатными циф-
рами любой позиционной системы счисления, обеспечивающими исправление
соответствующих им групп ошибок.
Вместе с тем необходимо отметить, что уже на начальных этапах исследо-
ваний совершенных кодов [9] высказывалось мнение, что «имеются некоторые
результаты, показывающие, что совершенных кодов мало, и кажется вполне
правдоподобным, что не существует других совершенных кодов», кроме из-
вестных в это время. В дальнейшем это предположение получило «подтвер-
Продолжение геометрического синтеза кодов, исправляющих ошибки
329
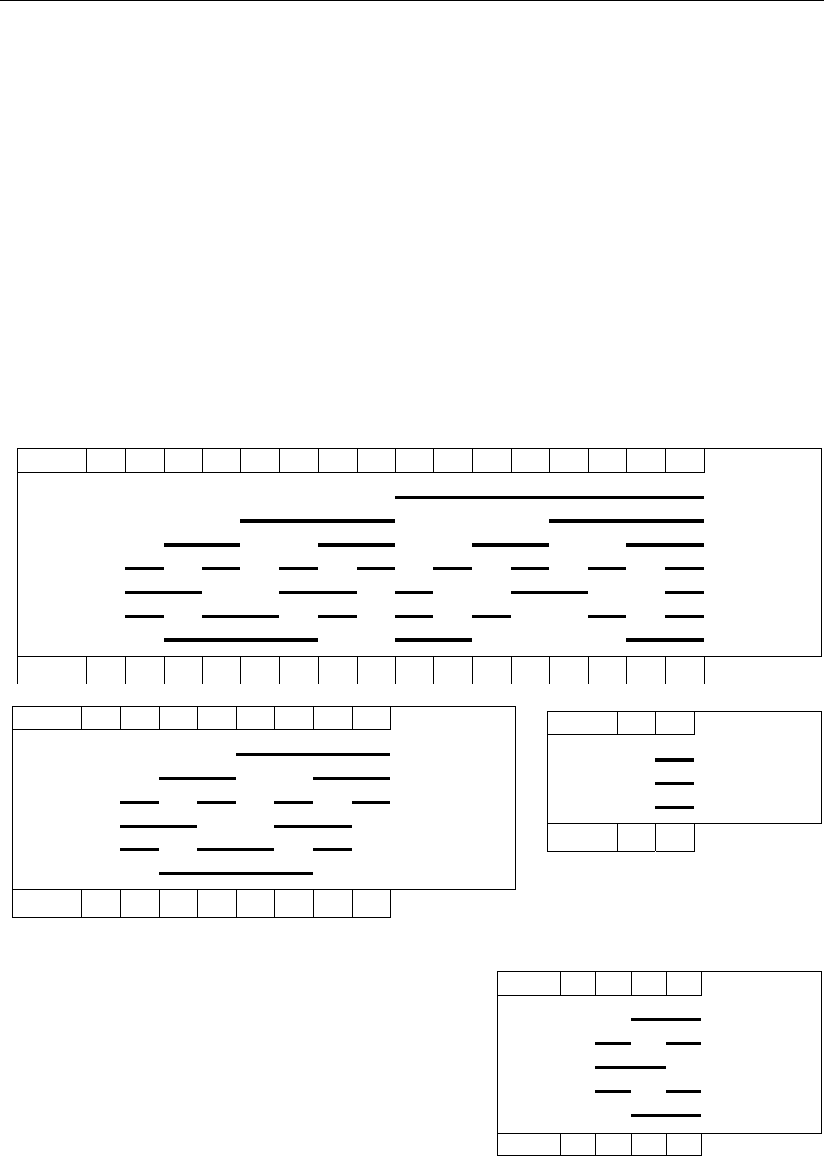
в)
Рис. 6.1
ждение» в работах финских [8] и советских [7] авторов, которые в 1972 г.
«строго доказали» отсутствие каких-либо совершенных двоичных кодов,
отличных от тех, которые были им известны. Позднее эти же авторы и амери-
канский ученый Ван Линт «получили полное решение вопроса о нахождении
всех совершенных кодов, использующих p
k
элементарных сигналов, где p –
произвольное число, а k – любое целое положительное число; таких кодов ока-
залось крайне мало» [10].
Ошибочность этих научных выводов показана в предыдущих главах книги:
число совершенных кодов, исправляющих все одиночные ошибки, как в ин-
формационной, так и контрольной части систематического кода, где информа-
ционная часть кода представляется в основном двоичном варианте, определяет-
ся выражением S = 2
k
(i !), в котором число контрольных разрядов k = 3, 4,
5, … , а соответствующее им число информационных разрядов определяется
выражением i = 2
k
– 1 – k (i = 4, 11, 26, …), неограниченно велико. Причем если
в качестве информационной части кода использовать любые двоичные коды
оснований систем счисления n =2
i
, тогда
число совершенных кодов будет увеличено:
S = 2
k
(i!) (2
i
!).
Число квазисовершенных кодов, кото-
рые являются образующими из совершенных
кодов оснований систем счисления
n = 2
4
,
2
11
, 2
26
…, также необозримо велико.
На рис. 6.1, а представлен пример со-
вершенного кода (k = 3, i = 4) соответственно
основанию n = 2
4
в его информацион-
ной части (координаты кода 0,3
W
a
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 W
i
a
4
8
a
3
4
a
2
2
a
1
1
x
3
4
(0,3)
x
2
2
x
1
1
к
0 6 5 3 3 5 6 0 7 1 2 4 4 2 1 7
а)
W
a
0 1 2 3 4 5 6 7
W
i
a
3
4
a
2
2
a
1
1
x
3
4
(0,3)
x
2
2
x
1
1
к
0 6 5 3 3 5 6 0
б)
W
a
0 1 2 3
W
i
a
2
2
a
1
1
x
3
4
(0,3)
x
2
2
x
1
1
к
0 6 5 3
и 0 1
W
i
a
1
1
x
3
2
x
2
1
(0,3)
к
0 6
г)
