Кочергин В.И. Теория многомерных цифро-векторных множеств
Подождите немного. Документ загружается.


Глава 2
100
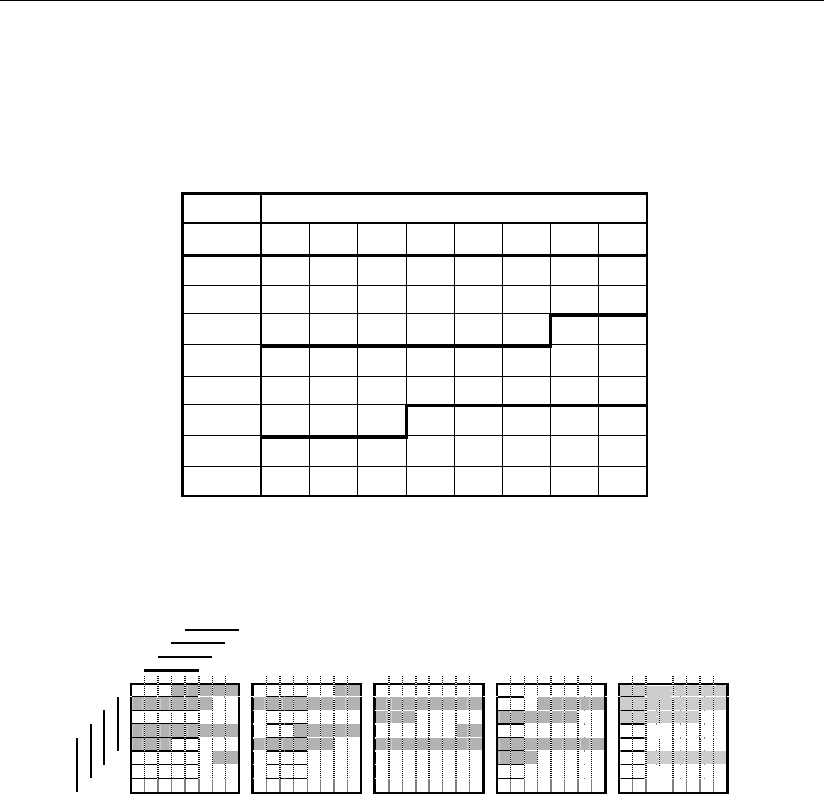
Сигналы, представленные на рис. 2.5, определяются по следующим логиче-
ским зависимостям:
Выполнение операции умножения на константу «два» было рассмотрено
выше и не требует дополнительных пояснений.
a
4
a
3
a
2
a
1
A
0 1 2 3 4 5 6 7
A×2
0 2 4 6 0 2 4 6
с
1
= с
2
с
3
= с
4
A×3
0 3 6 1 4 7 2 5
d
1
d
2
d
3
d
4
A×4
0 4 0 4 0 4 0 4
h
1
=h
2
=h
3
=h
4
A×5
0 5 2 7 4 1 6 3
f
1
=d
4
f
2
=d
3
f
3
=d
2
f
4
=d
1
A×6
0 6 4 2 0 6 4 2
r
1
=r
2
=c
3
r
3
=r
4
=c
1
A×7
0 7 6 5 4 3 2 1
s
1
=a
4
s
2
=a
3
s
3
=a
2
s
4
=a
1
Рис. 2.5
c
1
= c
2
=
(a
1
⊗
a
3
)
;
c
3
= c
4
=
(a
2
⊗
a
4
)
;
d
1
=
a
1
a
2
∨
a
1
a
3
∨
a
2
a
3
;
d
2
=
a
1
a
2
∨
a
1
a
4
∨
a
2
a
4
;
d
3
=
a
1
a
3
∨
a
1
a
4
∨
a
3
a
4
;
d
4
=
a
2
a
3
∨
a
2
a
4
∨
a
3
a
4
;
h
1
= ...=
h
4
=
(a
1
⊗
a
2
)
(a
3
⊗
a
4
)
;
f
1
=d
4
, f
2
=d
3
, f
3
=d
2
, f
4
=d
1
;
r
1
=r
2
=c
3
; r
3
=r
4
=c
1
;
s
1
=
a
4
, s
2
=
a
3
, s
3
=
a
2
, s
4
=
a
1
. (2.1.2)
Синтез умножителей, делителей и счетчиков
101
Умножение на константу «три» для второго разряда результата умножения
представляется табл. 2.1.1, где «единицы» результата умножения во втором
разряде суммируются с «восьмерками» (переносами) с первого разряда этой же
операции умножения.
Результат этой двойной операции (умножения и суммирования) представ-
лен графически на рис. 2.6а для сигналов d
2
1
– d
2
4
и цифр переноса P
2
d
в третий
разряд устройства.
Из рис. 2.6а видно, что геометрические образы сигналов d
2
1
– d
2
4
на второй
половине двухмерного цифрового пространства равны инверсии этих образов
первой половины пространства. Следовательно, в дальнейшем можно изобра-
жать только одну половину геометрических образов этих сигналов, поскольку
вторая половина этих образов очевидна.
Проделав эти же двойные операции в третьем разряде, можно получить
цифровые множества сигналов d
3
1
– d
3
4
и переноса P
3
d
в четвертый разряд уст-
ройства.
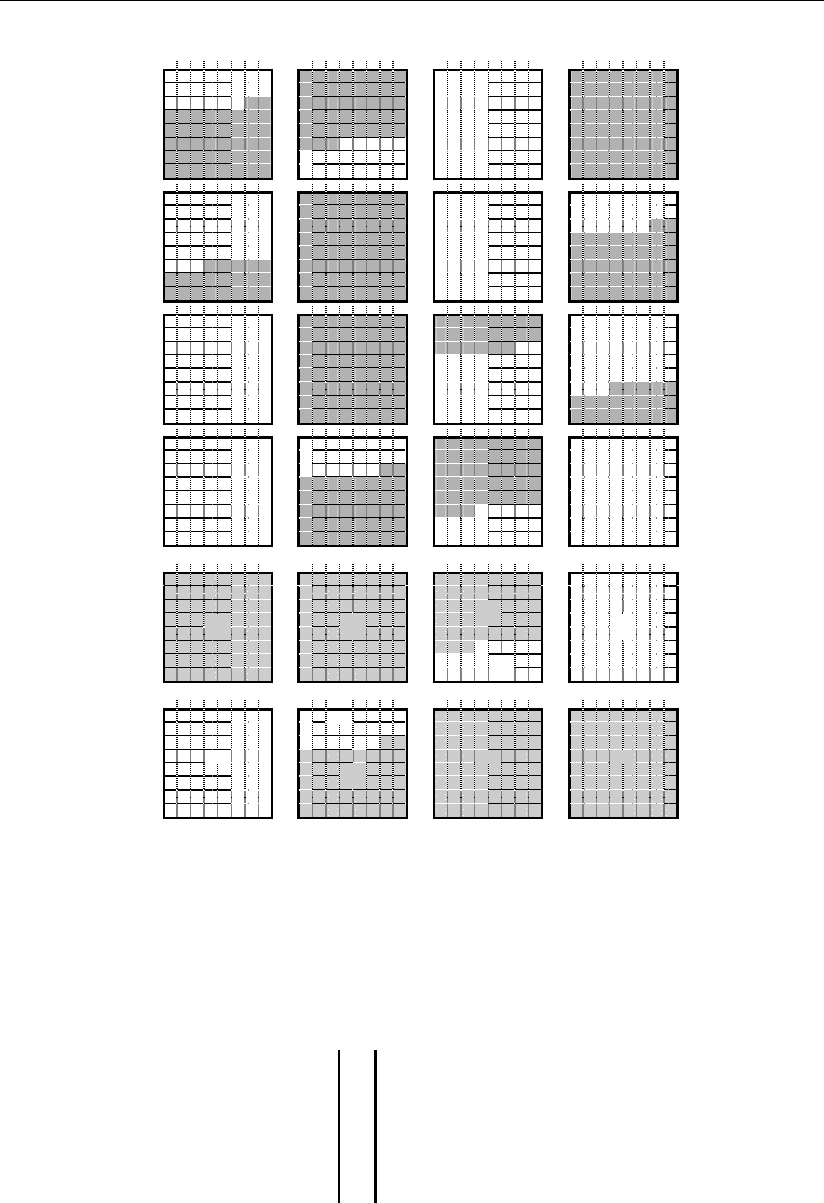
Для этого построим трехмерную табл. 2.1.1
'
, где «единицы» результата ум-
ножения в третьем разряде суммируются с «восьмерками» P
2
d
, поступающими
со второго разряда этой операции умножения.
Таблица 2.1.1
Перенос с A
1
A
2
×3 0 0 0 1 1 1 2 2
00
0 0 0 1 1 1 2 2
03
3 3 3 4 4 4 5 5
06
6 6 6 7 7 7 10 10
11
11 11 11 12 12 12 13 13
14
14 14 14 15 15 15 16 16
17
17 17 17 20 20 20 21 21
22
22 22 22 23 23 23 24 24
25
25 25 25 26 26 26 27 27
A
1
0
A
2
1
2
d
2
1
d
2
2
d
2
3
d
2
4
P
2
d
Рис. 2.6а

Глава 2
102
Эта процедура построения таблицы и на ее основе геометрических образов
соответствующих сигналов выполняется следующим образом.
Геометрические образы сигналов d
3
1
– d
3
4
будем представлять только на
первой половине трехмерного цифрового пространства (цифры 0–3 третьего
разряда A
3
), а образ сигнала переноса P
3
d
, поскольку он не имеет симметрии в
этом пространстве, будем представлять полностью.
Рассмотрим вначале геометрический образ сигнала d
3
1
. Для цифры 0 (A
3
) ум-
ножение на «три» остается без последствий, и сигнал переноса P
2
d
(см. рис. 2.6а)
полностью определяет в таблице результат умножения на константу «три» для
третьего разряда генератора кратностей.
Для цифры 1 (A
3
) умножение на «три» дает результат 03 и сигнал переноса
P
2
d
, который с ней суммируется и полностью определяет результат умножения
на константу «три» в третьем разряде генератора кратностей, и т.д.
Учитывая, что d
1
= 1 ∨ 2 ∨ 3 ∨ 4, d
2
= 2 ∨ 3 ∨ 4 ∨ 5, d
3
= 3 ∨ 4 ∨ 5 ∨ 6,
d
4
= 4 ∨ 5 ∨ 6 ∨ 7, геометрические образы всех этих сигналов изображаются на
рис. 2.6б в трехмерном цифровом пространстве (A
1
, A
2
, A
3
).
Аналогично из этой таблицы определяется геометрический образ сигнала
переноса P
3
d
, который также изображен на рис. 2.6б.
В дальнейшем описании работы генератора кратностей для мерности про-
странства больше трех подобные детали в построении геометрических образов
выходных сигналов генератора кратностей из-за их очевидности будем опус-
кать.
Таблица 2.1.1
0
1
2
3
A
1
0 1 2 3 4 5 6 7
0
1
2
00
03 06 11
A
2
3
4
01
04 07 12
5
6
7
02
05 10 13
4
5
6
7
14
17 22 25
15
20 23 26
16
21 24 27
Синтез умножителей, делителей и счетчиков
103
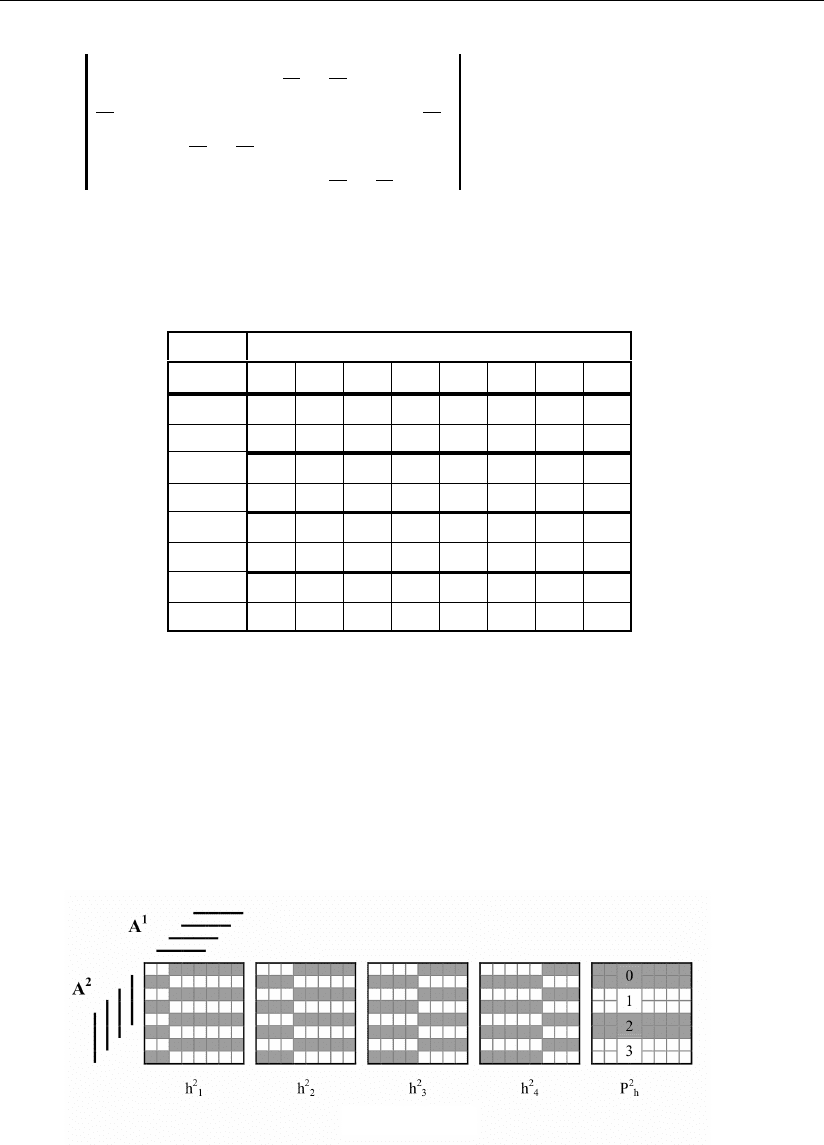
При этом геометрические образы всех выходных сигналов генератора крат-
ностей в трехмерном цифровом пространстве (A
1
, A
2
, A
3
) будем представлять
также послойно и термин «послойно» в дальнейшем упоминать не будем.
Результаты этих операций для k-го разряда устройства в матричной форме
запишутся следующим образом:
0 1 2 3
A
3
d
3
1
d
3
2
d
3
3
d
3
4
A
3
0 1 2 3
0
0 0 1
P
3
d
1
A
3
4 5 6 7
1
1 2 2
P
3
d
2
Рис. 2.6б
0
k
.
.
,
D
k
= M
k
d
.
7 A
Глава 2
104
где
Матрица цифровых множеств M
k
D
определяется по следующей записи:
для k= 2 m
1
= (3 ∨ ... ∨ 7)
1
; m
2
= (0 ∨ ... ∨ 5)
1
, а для k= 3 m
1
= (3 ∨ ... ∨ 7)
2
∨ (6 ∨ 7)
1
a
2
2
;
m
2
= (0 ∨ ... ∨ 5)
2
∨ (0 ∨ 1 ∨ 2)
1
a
2
2
и т.д.
Умножение на константу «четыре» для второго разряда результата умноже-
ния представлено в табл. 2.1.2.
Простота этой таблицы и симметрия расположения цифровых данных в
двухмерном цифровом пространстве координат первого и второго разрядов оп-
ределяют простые геометрические образы сигналов фаз и сигналов переноса в
третий разряд генератора кратностей.
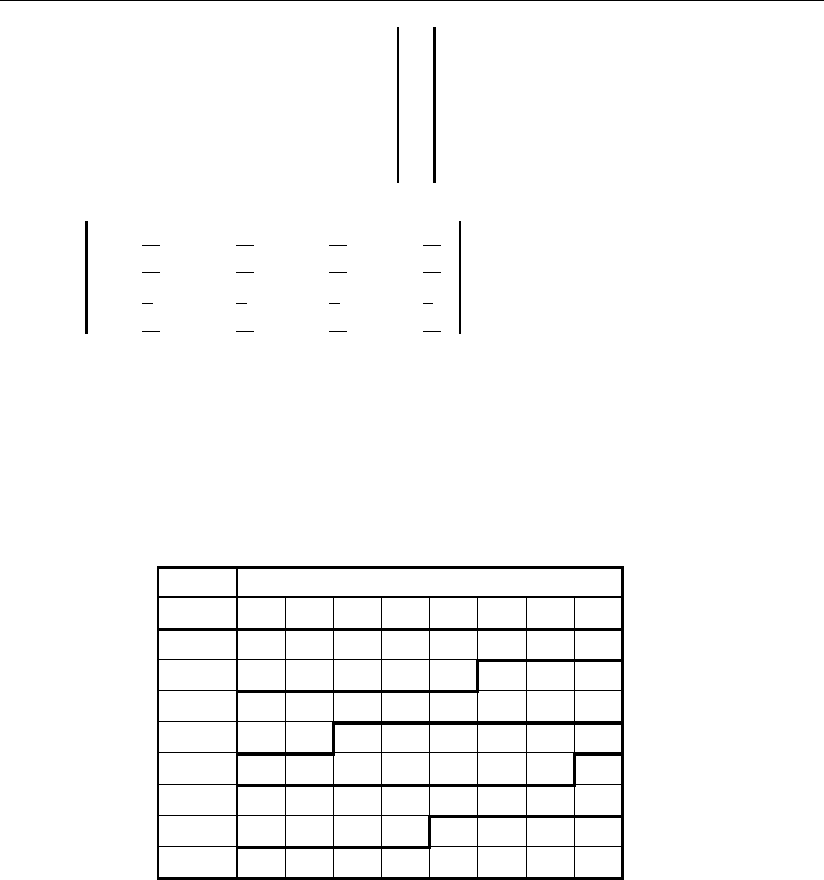
Результат этой двойной операции показан графически на рис. 2.7 для сигна-
лов h
2
1
– h
2
4
и цифр переноса P
2
H
в третий разряд устройства.
Поскольку для умножения на константу «четыре» нет сквозного переноса
через разряд, то можно сразу записать результат операции для k-го разряда уст-
ройства:
m
1
m
2
0* 1* m
1
m
2
1* 0* k
M
k
D
=
m
2
1* 0* m
1
m
2
0* 1* m
1
0* 1* m
1
m
2
1* 0* m
1
m
2
.
0* m
1
m
2
0* 1* m
1
m
2
1*
D
(2.1.3)
Таблица 2.1.2
Перенос с A
1
A
2
×4 0 0 1 1 2 2 3 3
00
0 0 1 1 2 2 3 3
04
4 4 5 5 6 6 7 7
10
10 10 11 11 12 12 13 13
14
14 14 15 15 16 16 17 17
20
20 20 21 21 22 22 23 23
24
24 24 25 25 26 26 27 27
30
30 30 31 31 32 32 33 33
34
34 34 35 35 36 36 37 37
Рис. 2.7
Синтез умножителей, делителей и счетчиков
105
0
k
.
.
.
H
k
= M
k
h
,
7
A
где
m
1
m
1
m
1
m
1
m
1
m
1
m
1
m
1
k
M
k
H
=
m
2
m
2
m
2
m
2
m
2
m
2
m
2
m
2
a
4
a
4
a
4
a
4
a
4
a
4
a
4
a
4
,
m
3
m
3
m
3
m
3
m
3
m
3
m
3
m
3
H
(2.1.4)
а m
k
1
= (2 ∨ ... ∨ 7)
k
, m
k
2
= (3 ∨ ... ∨ 7)
k
, m
k
3
= (5 ∨ ... ∨ 7)
k
и h
k+1
1
= m
k
1
=
=(2 ∨ ... ∨ 7)
k
, h
k+1
2
= a
k
4
,
h
k+1
3
= (6 ∨ 7)
k
.
Умножение на константу «пять» для второго разряда умножения представ-
ляется данными табл. 2.1.3.
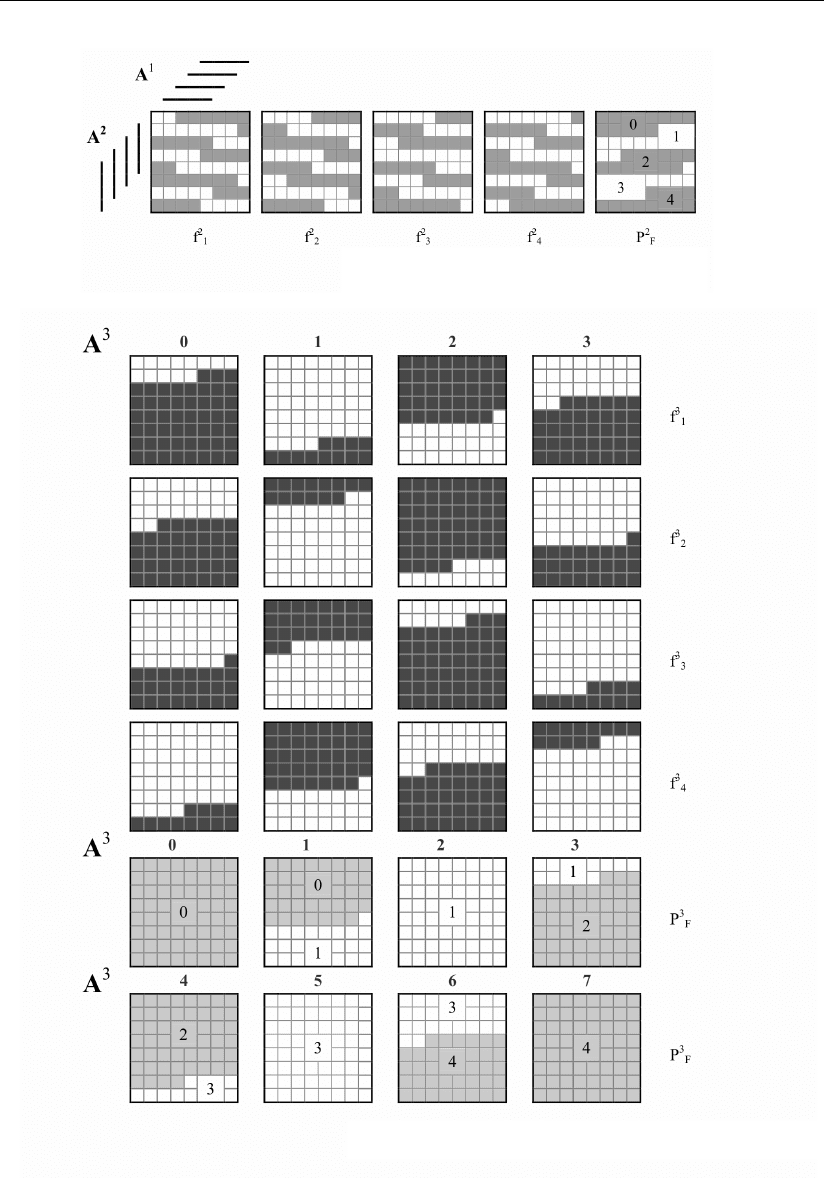
Результат этой двойной операции показан графически на рис. 2.8, а для
сигналов f
2
1
– f
2
4
и цифр сигнала переноса P
2
F
в третий разряд устройства.
Выполнив такие же двойные операции в третьем разряде устройства, мож-
но представить цифровые множества сигналов f
2
1
– f
2
4
и цифр сигнала переноса
P
2
F
в четвертый разряд устройства, что и показано на рис. 2.8, б в трехмерном
цифровом пространстве.
Таблица 2.1.3
Перенос с A
1
A
2
×5 0 0 1 1 2 3 3 4
00
0 0 1 1 2 3 3 4
05
5 5 6 6 7 10 10 11
12
12 12 13 13 14 15 15 16
17
17 17 20 20 21 22 22 23
24
24 24 25 25 26 27 27 30
31
31 31 32 32 33 34 34 35
36
36 36 37 37 40 41 41 42
43
43 43 44 44 45 46 46 47
Глава 2
106
а)
б)
Рис. 2.8
Синтез умножителей, делителей и счетчиков
107
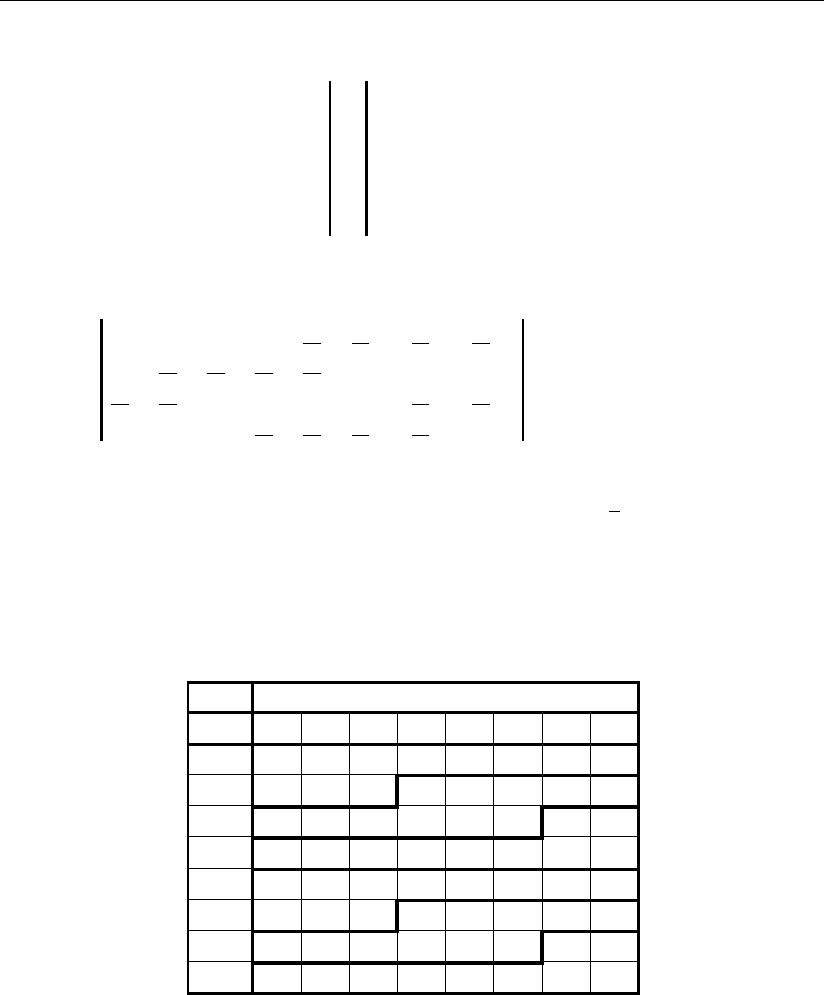
Результат умножения для k-го разряда устройства в матричной форме запи-
си:
где
Для k=2 m
1
= (2∨ ... ∨7)
1
, m
2
= 7
1
, m
3
= (0 ∨ ... ∨ 4)
1
, m
4
= a
1
4;
а для k=3
m
1
= (2 ∨ ... ∨ 7)
2
∨ (5 ∨ 6 ∨ 7)
1
a
2
1
, m
2
= 7
2
∨ a
1
4
(5 ∨ 6)
2
, m
3
= a
2
4
∨ (0 ∨ ... ∨ 6)
1
a
2
1
,
m
4
= a
2
4
∨ (2 ∨ ... ∨ 7)
1
a
2
3
и т.д.
Результаты умножения на константу «шесть» для второго разряда опреде-
ляются данными табл. 2.1.4.
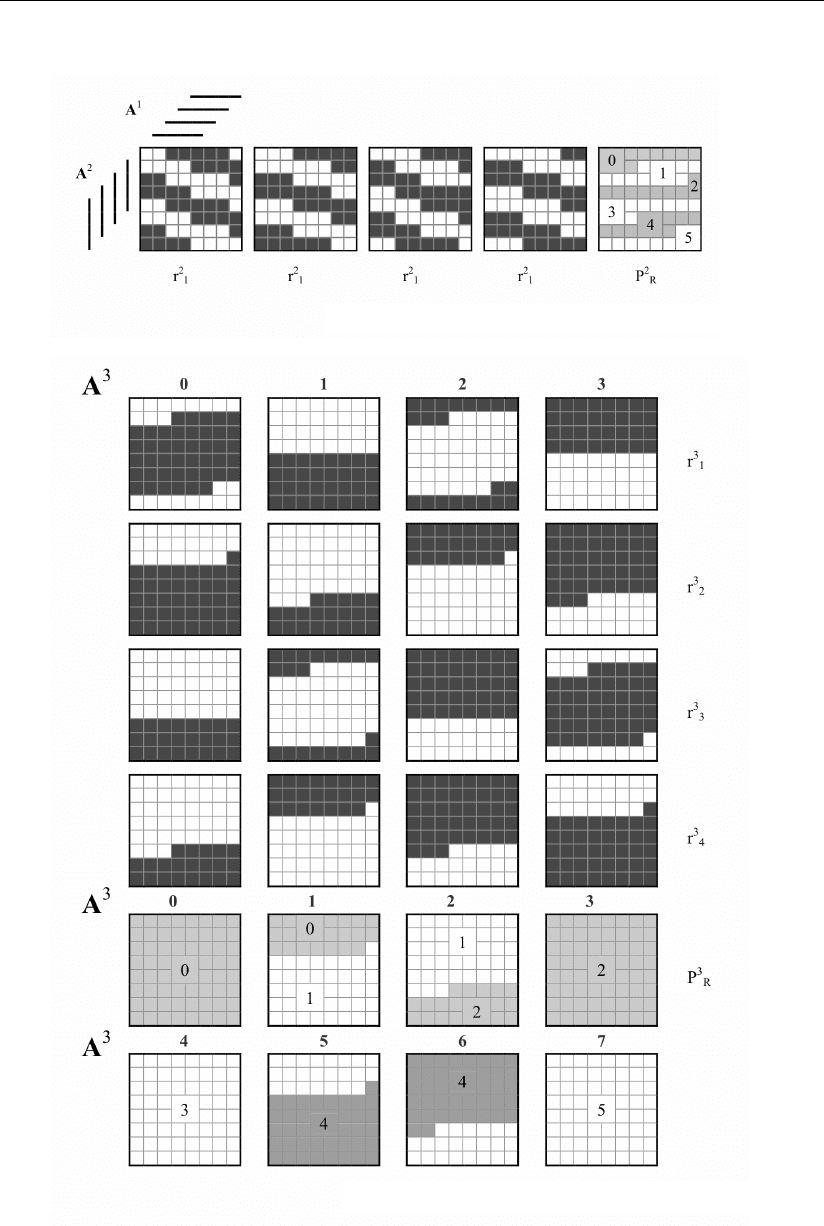
Результат этой двойной операции изображен графически на рис. 2.9, а для
сигналов r
2
1
– r
2
4
и цифр сигнала переноса P
3
R
в третий разряд устройства.
Выполнив аналогичные двойные операции в третьем разряде, можно пред-
ставить цифровые множества сигналов r
2
1
– r
2
4
и цифр сигналов переноса P
3
R
в
четвертый разряд устройства, что приведено на рис. 2.9, б в трехмерном циф-
ровом пространстве.
0
k
.
.
F
k
= M
k
f
.
,
7
A
m
1
m
2
m
3
m
4
m
1
m
2
m
3
m
4
k
M
k
F
=
m
4
m
1
m
2
m
3
m
4
m
1
m
2
m
3
m
3
m
4
m
1
m
2
m
3
m
4
m
1
m
2
.
m
2
m
3
m
4
m
1
m
2
m
3
m
4
m
1
F
(2.1.5)
Таблица 2.1.4
Перенос с A
1
A
2
×6 0 0 1 2 3 3 4 5
00
0 0 1 2 3 3 4 5
06
6 6 7 10 11 11 12 13
14
14 14 15 16 17 17 20 21
22
22 22 23 24 25 25 26 27
30
30 30 31 32 33 33 34 35
36
36 36 37 40 41 41 42 43
44
44 44 45 46 47 47 50 51
52
52 52 53 54 55 55 56 57
Глава 2
108
б)
Рис. 2.9
а)
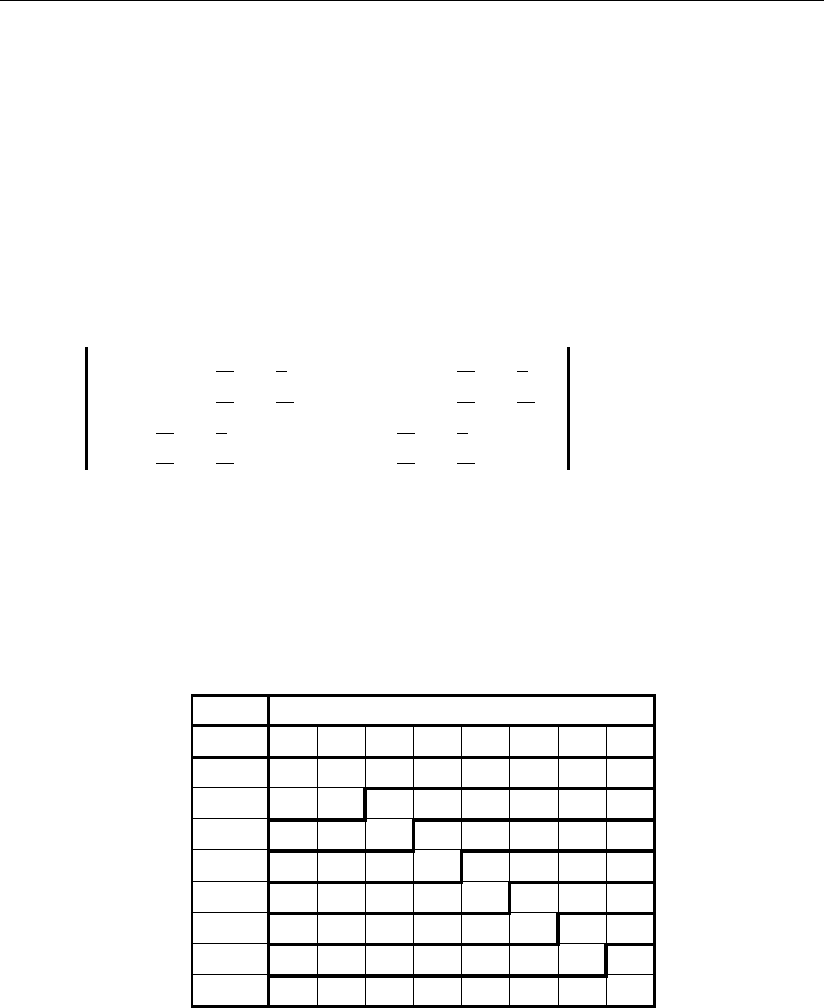
Синтез умножителей, делителей и счетчиков
109
Результат умножения для k-го разряда устройства в матричной форме запи-
си:
где
Для k= 2 m
1
= (2 ∨ ... ∨ 6)
1
, m
2
= (3 ∨ ... ∨ 7)
1
, m
3
= (6∨ 7)
1
; а для k= 3
m
1
= (2 ∨ ... ∨ 6)
2
(1 ∨ ... ∨ 5)
1
∨ (1 ∨ ... ∨ 5)
2
(3 ∨ ... ∨ 7)
1
, m
2
= (3 ∨ ... ∨ 7)
2
∨ 7
1
a
2
2
,
m
3
= (7 ∨ 6)
2
∨ (3 ∨ ... ∨ 7)
1
(5 ∨ 6 ∨ 7)
2
и т.д.
Умножение на константу «семь» для второго разряда умножения представ-
ляется данными табл. 2.1.5.
Результат этой двойной операции изображен графически на рис. 2.10, а для
сигналов s
2
1
– s
2
4
и цифр переноса P
2
S
в третий разряд устройства.
0
k
.
.
R
k
= M
k
R
.
,
7
A
m
1
a
k
–
1
4
m
1
a
k
–
1
4
m
1
a
k
–
1
4
m
1
a
k
–
1
4
k
M
k
R
=
m
2
m
3
m
2
m
3
m
2
m
3
m
2
m
3
a
k–1
4
m
1
a
k–1
4
m
1
a
k–1
4
m
1
a
k–1
4
m
1
.
m
3
m
2
m
3
m
2
m
3
m
2
m
3
m
2
R
(2.1.6)
Таблица 2.1.5
Перенос с A
1
A
2
×7 0 0 1 2 3 4 5 6
00
0 0 1 2 3 4 5 6
07
7 7 10 11 12 13 14 15
16
16 16 17 20 21 22 23 24
25
25 25 26 27 30 31 32 33
34
34 34 35 36 37 40 41 42
43
43 43 44 45 46 47 50 51
52
52 52 53 54 55 56 57 60
61
61 61 62 63 64 65 66 67
