Кочергин В.И. Теория многомерных цифро-векторных множеств
Подождите немного. Документ загружается.

Глава 1
80
n = 8, где одновременно с сигналами разрядов кода (a
1
, a
2
, a
3
) приведены циф-
ровые 0–7 и весовые 0–7 значения его кодовых комбинаций.
3
2
A
1
C = (A + B), A, B, C – в коде Грея, P
n–1
= 0*
0 1 2 3 4 5 6 7
0 1 3 2 6 7 5 4 0 1326754 01326754 0 1 3 2 6 7 5 4
B
1 0 0
** **
0
****
0
****
0
2 1 1
** **
1
****
1
****
1
*
2 3
* ** *
3
****
3
****
3
**
3 3 2
** **
2
*** *
2
****
2
***
4 6
** **
6
** **
6
****
6
****
5 7
** **
7
* ***
7
*** *
7
*****
6 5
* ** *
5
****
5
** **
5
******
7 4
** **
4
****
4
* ***
4
*******
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
* * * *
0
** **
0
****
0
1
** **
1
*** *
1
****
1
*
2
****
2
** **
2
*** *
2
** *
3
* * * *
3
****
3
** **
3
**
4
****
4
****
4
****
4
*******
5
* * * *
5
****
5
** **
5
******
6
* * * *
6
** **
6
****
6
****
P
n–1
= 0*
7
** **
7
****
7
** **
7
*****
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
** **
0
*** *
0
****
0
*
1
* * * *
1
****
1
** **
1
**
2
* * * *
2
** **
2
****
2
****
3
****
3
** **
3
*** *
3
** *
4
* * * *
4
** **
4
****
4
********
5
****
5
****
5
****
5
*******
6
** **
6
****
6
** **
6
*****
P
n–1
= 1*
7
* * * *
7
****
7
** **
7
******
c
1
c
2
c
3
P
n
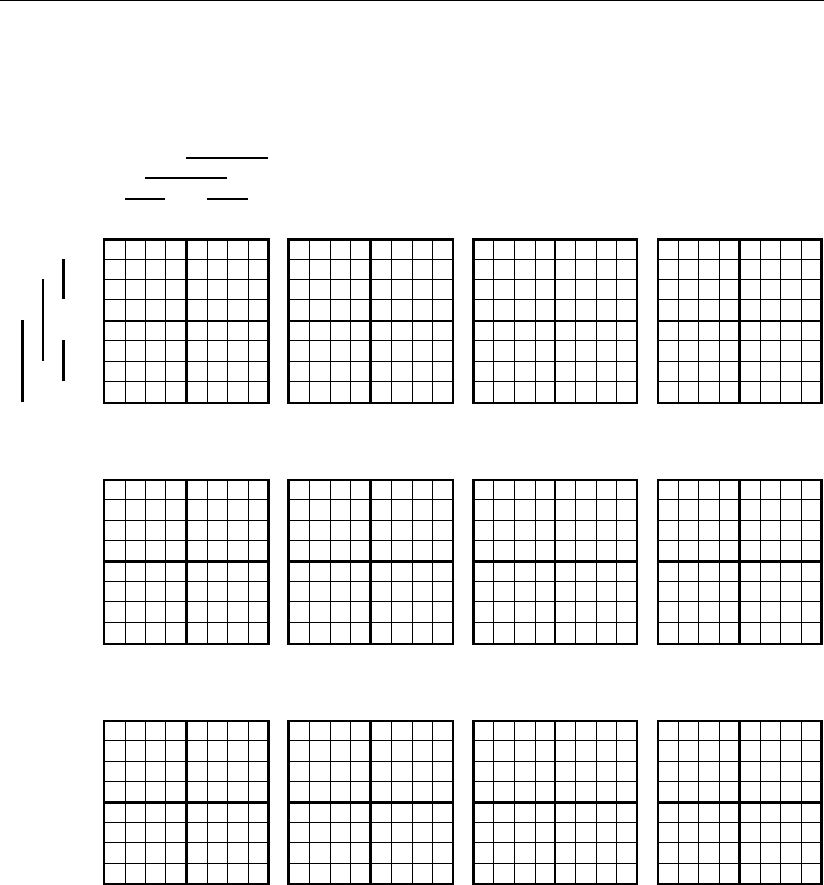
Рис. 1.28
Цифровые значения кодовых комбинаций всегда используются для по-
строения геометрических образов сигналов разрядов на основании соответст-
вующих арифметических таблиц. На основании такой таблицы суммирования
на рис. 1.28 построены геометрические образы выходных сигналов сумматора
C = (A + B), когда во входных и выходных сигналах применяется код Грея, при
входных сигналах переносов P
n–1
= 0* и P
n–1
= 1*.
Основные положения теории
81
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
** **
0
****
0
1
****
1
****
1
****
1
*
2
** **
2
****
2
** **
2
** *
3
****
3
****
3
** **
3
**
4
** **
4
*** *
4
****
4
**** ***
5
****
5
****
5
** **
5
**** **
6
****
6
** **
6
****
6
****
C = (A – B)
Z
n–1
= 0*
7
****
7
** **
7
*** *
7
**** *
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
****
0
****
0
*
1
****
1
****
1
** **
1
**
2
****
2
** **
2
****
2
****
3
** **
3
****
3
** **
3
** *
4
****
4
** **
4
****
4
********
5
** **
5
*** *
5
****
5
**** ***
6
****
6
** **
6
*** *
6
**** *
C = (A – B)
Z
n–1
= 1*
7
****
7
****
7
** **
7
**** **
c
1
c
2
c
3
Z
n
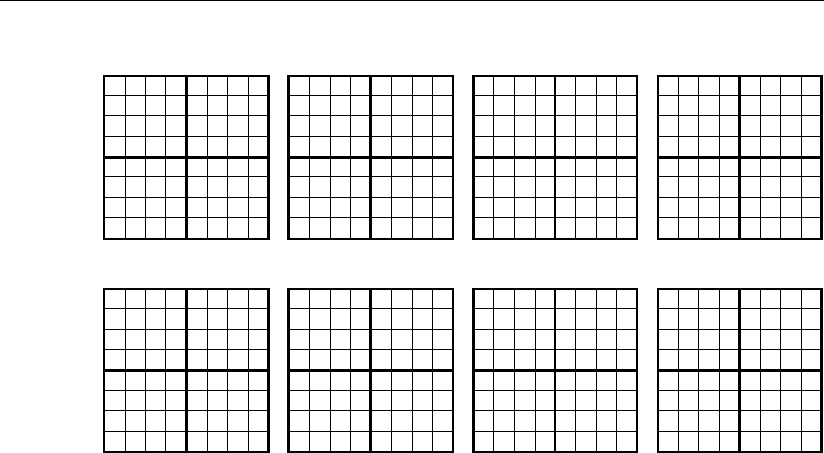
Рис. 1.29
Для входного сигнала переноса P
n–1
= 0* построение геометрических об-
разов выходных сигналов c
1
, c
2
, c
3
, P
n
первоначально выполнено в цифровых
значениях координат входных сигналов A, B (первый ряд геометрических фи-
гур этих сигналов на рис. 1.28), а в дальнейшем представлены изменения этих
фигур при последовательном переходе к весовым значениям координат основ-
ного двоичного кода.
На этом же рисунке в четвертом ряду фигур изображены геометрические
фигуры выходных сигналов сумматора при P
n–1
= 1*, минуя промежуточные
преобразования, сразу в координатах основного двоичного кода.
Для режима вычитания C = (A – B) аналогичные геометрические фигуры
приведены, минуя представление промежуточных геометрических преобразо-
ваний, на рис. 1.29 соответственно при Z
n-1
= 0*, Z
n-1
= 1*.
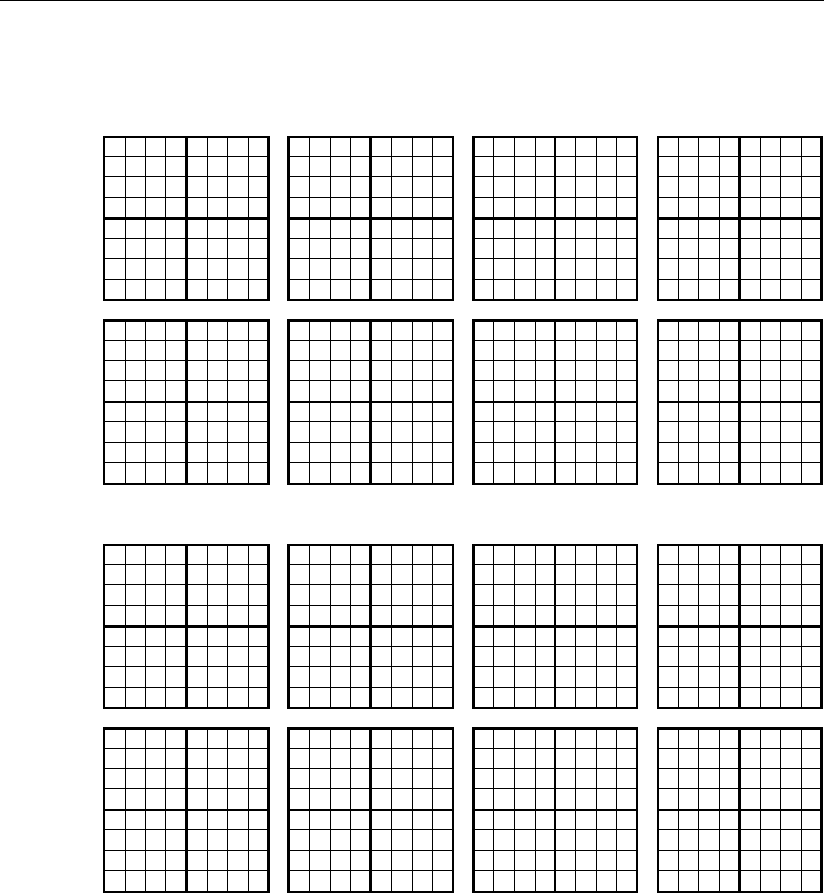
Применение в суммирующих блоках иных возможных сочетаний кодов
представлено, также минуя представление промежуточных геометрических
преобразований, в двух вариантах: на рис. 1.30, когда операнды A, B – в коде
Грея, а выходной сигнал C = (A ± B) – в основном двоичном коде; на
рис. 1.31, когда операнд A – в коде Грея, а операнд B и выходной сигнал
C = (A ± B) – в основном двоичном коде.
Дальнейшие этапы синтеза логических функций сумматоров C = (A ± B),
определяющие их схемотехнические решения, будут выполняться на основании
покрытия выходных сигналов их геометрических образов. Это покрытие долж-
но выполняться в соответствии с требованием быстродействия сумматоров, что
определяет необходимый уровень схемного решения. Очевидно, предельное
быстродействие будет получено в двухуровневой схеме сумматора.

Глава 1
82
A, B – в коде Грея, C – в основном двоичном коде
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
** * *
0
****
0
****
0
1
****
1
****
1
****
1
*
2
****
2
****
2
*** *
2
** *
3
** * *
3
** **
3
***
3
**
4
****
4
****
4
****
4
*******
5
** * *
5
** **
5
** ***
5
******
6
** * *
6
****
6
****
6
****
C = A + B
P
n–1
= 0*
7
****
7
****
7
** **
7
*****
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
****
0
****
0
*
1
** * *
1
** **
1
** **
1
**
2
** * *
2
****
2
****
2
****
3
****
3
****
3
*** *
3
** *
4
** * *
4
****
4
****
4
********
5
****
5
****
5
****
5
*******
6
****
6
****
6
** **
6
*****
C = A + B
P
n–1
= 1*
7
** * *
7
** **
7
** **
7
******
c
1
c
2
c
3
P
n
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
** * *
0
****
0
****
0
1
****
1
****
1
****
1
*
2
****
2
****
2
** **
2
** *
3
** * *
3
** **
3
** **
3
**
4
****
4
****
4
****
4
**** ***
5
** * *
5
** **
5
** **
5
**** **
6
** * *
6
****
6
****
6
****
C = A – B
Z
n–1
= 0*
7
****
7
****
7
*** *
7
**** *
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
****
0
****
0
*
1
** * *
1
** **
1
** **
1
**
2
** * *
2
****
2
****
2
****
3
****
3
****
3
** **
3
** *
4
** * *
4
****
4
****
4
********
5
****
5
****
5
****
5
**** ***
6
****
6
****
6
*** *
6
**** *
C = A – B
Z
n–1
= 1*
7
** * *
7
** **
7
** **
7
**** **
c
1
c
2
c
3
Z
n
Рис. 1.30
Первоначально в качестве примера многоуровневого синтеза сумматора
C = (A ± B) рассмотрим такой вариант схемного решения, когда все входные
сигналы и результат операции представляются в коде Грея. Для этого обратим-
ся к геометрическим образам (см. рис. 1.28, 1.29) его выходных сигналов c
1
, c
2
,
c
3
, P
n
, Z
n
и рассмотрим их подмножества в каждой четверти пространства коор-
динат основного двоичного кода.
Основные положения теории
83
A – в коде Грея; B, C – в основном двоичном коде
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
** * *
0
****
0
****
0
1
****
1
****
1
****
1
*
2
** * *
2
** **
2
** **
2
**
3
****
3
****
3
*** *
3
** *
4
** * *
4
****
4
****
4
****
5
****
5
****
5
** **
5
*****
6
** * *
6
** **
6
** **
6
******
C = A + B
P
n–1
= 0*
7
****
7
****
7
****
7
*******
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
****
0
****
0
*
1
** * *
1
** **
1
** **
1
**
2
****
2
****
2
*** *
2
** *
3
** * *
3
****
3
****
3
****
4
****
4
****
4
** **
4
*****
5
** * *
5
** **
5
** **
5
******
6
****
6
****
6
****
6
*******
C = A + B
P
n–1
= 1*
7
** * *
7
****
7
****
7
********
c
1
c
2
c
3
P
n
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
** * *
0
****
0
****
0
1
****
1
****
1
****
1
*
2
** * *
2
** **
2
** **
2
**
3
****
3
****
3
** **
3
** *
4
** * *
4
****
4
****
4
****
5
****
5
****
5
*** *
5
**** *
6
** * *
6
** **
6
** **
6
**** **
C = A – B
Z
n–1
= 0*
7
****
7
****
7
****
7
**** ***
0 1 2 3 4 5 6 7 0 1234567 01234567 0 1 2 3 4 5 6 7
0
****
0
****
0
****
0
*
1
** * *
1
** **
1
** **
1
**
2
****
2
****
2
** **
2
** *
3
** * *
3
****
3
****
3
****
4
****
4
****
4
*** *
4
**** *
5
** * *
5
** **
5
** **
5
**** **
6
****
6
****
6
****
6
**** ***
C = A – B
Z
n–1
= 1*
7
** * *
7
****
7
****
7
********
c
1
c
2
c
3
Z
n
Рис. 1.31
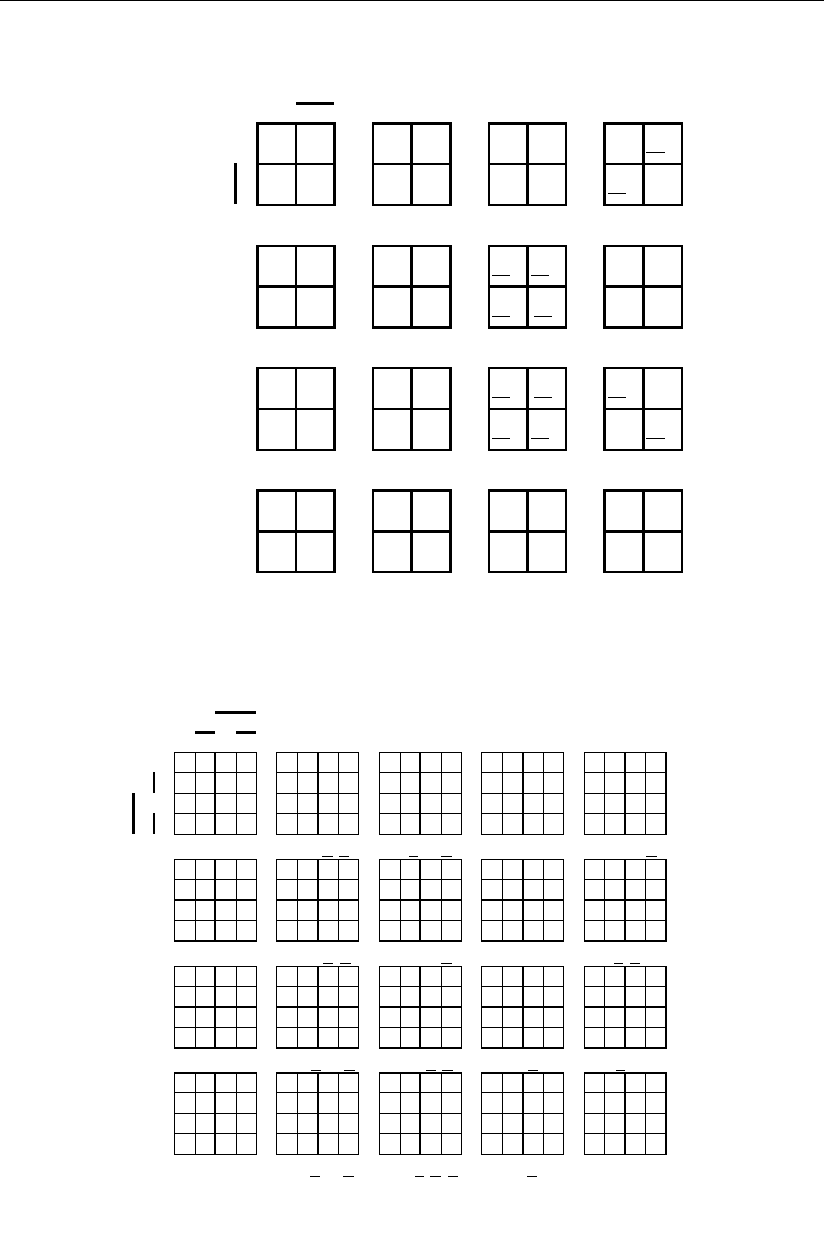
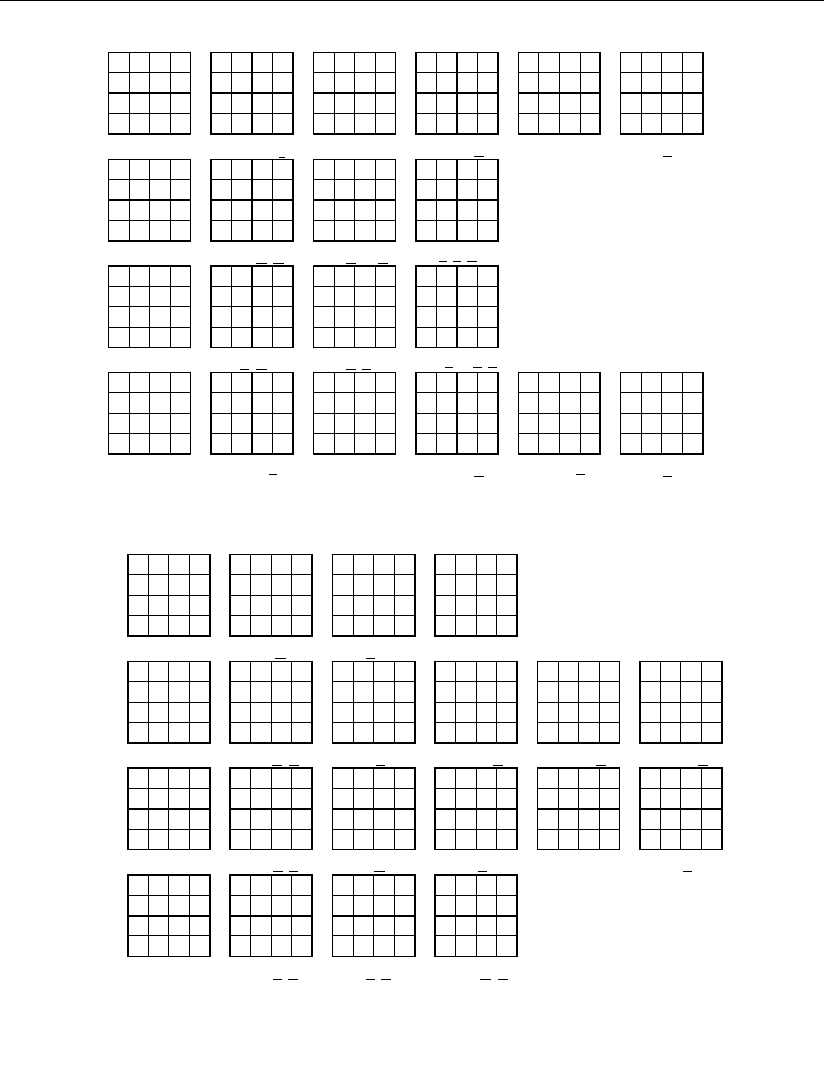
На рис. 1.32 изображены эти подмножества М
1
– М
12
, а на рис. 1.32, а – б
приведены более мелкие подмножества, их составляющие, которые представ-
лены соответствующими логическими выражениями и пронумерованы курси-
вом цифрами красного цвета.
Глава 1
84
a
3
b
3
М
1
М
2
М
5
М
6
М
9
М
10
М
10
C = (A + B),
P
n-1
= 0*
М
3
М
4
М
7
М
8
М
11
М
12
М
11
1*
c
1
c
2
c
3
P
n
М
4
М
3
М
8
М
7
М
12
М
11
М
11
C = (A + B),
P
n-1
= 1*
М
2
М
1
М
6
М
5
М
10
М
9
М
10
1*
c′
1
c′
2
c′
3
P′
n
М
2
М
1
М
6
М
5
М
10
М
9
М
10
C = (A – B),
Z
n-1
= 0*
М
4
М
3
М
8
М
7
М
12
М
11
1*
М
11
c′′
1
c′′
2
c′′
3
Z
n
М
3
М
4
М
7
М
8
М
11
М
12
М
11
C = (A – B),
Z
n-1
= 1*
М
1
М
2
М
5
М
6
М
9
М
10
1*
М
10
c′′′
1
c′′′
2
c′′′
3
Z′
n
а)
2
A
1
B
1
**
* *
2
** **
М
1
** **
**
=
∨ ∨
**
∨
1 = a
1
b
1
b
2
2 = a
2
b
1
b
2
3 = a
1
b
1
b
2
4 = a
2
b
1
b
2
**
**
** **
М
2
** **
**
=
∨ ∨
**
∨
1 = a
1
b
1
b
2
5 = a
1
b
1
b
2
6 = a
1
b
1
b
2
7 = a
2
b
1
b
2
**
**
** **
М
3
** **
**
=
∨ ∨
∨
**
11 = a
1
b
1
b
2
8 = a
2
b
1
b
2
9 = a
1
b
1
b
2
10 = a
2
b
1
b
2
**
**
** **
М
4
** **
**
=
∨ ∨
∨
**
11 = a
1
b
1
b
2
12 = a
2
b
1
b
2
9 = a
1
b
1
b
2
13 = a
2
b
1
b
2
Рис. 1.32 (на
ч
ало)
б)
Основные положения теории
85
В соответствии с рис. 1.32, а – г, учитывая, что М
5
⊃ М
6
, М
5
⊃ М
7
, М
8
⊃
М
6
, М
8
⊃ М
7
, можно записать логические выражения, определяющие по-
строение сумматора C = (A + B) при P
n–1
= 0*:
г)
Рис. 1.32 (продолжение)
** * **
*** * * * **
М
5
** * * **
****
=
*
∨
**
∨ ∨
****
∨
**
14 = a
1
a
2
15 = a
1
b
1
16 = a
2
b
2
17 = b
1
b
2
18 = a
2
b
2
**
** *
**
М
6
**
=
∨ ∨
8 = a
2
b
1
b
2
19 = a
1
a
2
b
2
36 = a
1
a
2
b
1
b
2
*
*
М
7
** ** *
*
=
∨
*
∨
7 = a
2
b
1
b
2
20 = a
1
a
2
b
2
35 = a
1
a
2
b
1
b
2
*** * **
**** * * * ** ****
М
8
** * **
** *
=
*
∨
**
∨ ∨ ∨
**
21 = a
1
a
2
15 = a
1
b
1
16 = a
2
b
2
22 = b
1
b
2
18 = a
2
b
2
в)
**
М
9
*** * * **
**
=
∨
*
∨
**
9 = a
1
b
1
b
2
23 = a
1
a
2
b
1
24 = a
2
b
2
**** **** * ** * *
*** * ** * * **
М
10
**
**
=
∨
*
∨ ∨ ∨
**
25 = b
1
b
2
26 = a
1
a
2
16 = a
2
b
2
27 = a
1
b
2
28 = a
1
b
2
**
** * **
М
11
**** * **** ** * *
** *
=
*
∨ ∨
**
∨
**
∨
**
29 = a
1
a
2
30 = b
1
b
2
18 = a
2
b
2
31 = a
1
b
2
32 = a
2
b
1
** ***
* *
**
**
*
М
12
*
=
∨
*
∨
33 = a
2
b
2
34 = a
1
a
2
b
1
1 = a
1
b
1
b
2

Глава 1
86
Принимая в качестве базового варианта построения этого блока логиче-
ские выражения (1.13.1), остальные режимы работы сумматора могут быть по-
лучены путем соответствующих поворотов относительно осей симметрии
двухмерного пространства их геометрических образов в координатах основного
двоичного кода:
Выходные сигналы сумматора соответственно для каждого из этих режи-
мов, отличных от базового, подчиняются соответствующим двум поворотам
для сигналов c′
1
– c′
3
либо одному повороту для сигналов c′′
1
– c′′
3
, c′′′
1
– c′′′
3
,
которые совершаются относительно осей симметрии этого пространства. Это
правило не относится к сигналу переноса P′
n
, где
требуется поменять местами
входы операндов A и B. Поэтому базовый блок для сигнала переноса P
n
должен
будет выполняться автономным со своими входами для операндов A и B, а
также своими схемами формирования подмножеств М
10
, М
11
внутри этого ав-
тономного блока.
Можно предложить иной вариант формирования сигналов переноса и заема,
который не требует использования такого автономного блока, а именно, когда
сигнал переноса формируется по сигналам старших разрядов операндов a
3
, b
3
и
аналогичного выходного сигнала c
3
сумматора по логическому выражению
P
n
= a
3
b
3
∨ a
3
c
3
∨ b
3
c
3
.
В этом варианте суммирующего устройства при выполнении необходимых
переключений на его входных шинах, которые изменяют его режимы работы с
целью получения выходных сигналов c′
1
– c′
3
,
c′′
1
– c′′
3
, c′′′
1
– c′′′
3
, он будет авто-
матически сопровождаться получением необходимого сигнала переноса либо
заема.
Для синтеза суммирующего блока максимального быстродействия необхо-
димо реализовать покрытие геометрических образов каждого отдельно сигна-
лов c
1
, c
2
,c
3
, начиная «сверху вниз», т.е. рассматривая старшие ячейки много-
мерного пространства, в которых определяются первоначально элементарные
ячейки, общие для всех разрядов, если такие имеются. Затем рассматриваются
ячейки более младших разрядов и т.д. вплоть до полного покрытия всех гео-
метрических образов.
c
1
= М
1
a
3
b
3
∨ М
2
a
3
b
3
∨ М
3
a
3
b
3
∨ М
4
a
3
b
3
,
c
2
= М
5
a
3
b
3
∨ М
6
a
3
(или М
6
b
3
)∨ М
7
b
3
(или М
7
a
3
)∨ ∨ М
8
a
3
b
3
,
c
3
= М
9
a
3
b
3
∨ М
10
a
3
b
3
∨ М
11
a
3
b
3
∨ М
12
a
3
b
3
,
P
n
= М
10
a
3
∨ М
11
b
3
∨ a
3
b
3
. (1.13.1)
c′
1
= c
1
(A
•
B
•
), c′
2
= c
2
(A
•
B
•
),
c
′
3
= c
3
(A
•
B
•
), P
′
n
= P
n
(BA);
c′′
1
= c
1
(A
•
B ), c′′
2
= c
2
(A
•
B ), c′′
3
= c
3
(A
•
B ), Z
n
= P
n
(A
•
B);
c
1
= c
1
(A B
•
), c′′′
2
= c
2
(A B
•
), c′′′
3
= c
3
(A B
•
), Z′
n
= P
n
(A B
•
).
(1.13.2)

Основные положения теории
87
* * * * * * * * * * * *
** ** * * * *
**** ** **
* * * * * * * *
c
1
**** ** **
* * * * * * * *
* * * *
=
∨
* *
∨
* *
** **
1
* *
2
3
* *
Рис. 1.33
1 = a
1
b
1
b
2
b
3
∨ a
1
a
2
b
1
a
3
∨ a
1
a
2
b
1
a
3
; 2 = a
1
a
2
b
1
a
3
∨ a
1
a
2
b
1
a
3
;
3 = a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
∨
∨ a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
∨ a
1
a
2
a
3
b
3
b
2
.
(1.13.3)
** ** * * ** **
*** * * * * *
** ** * * **
**** * * *
c
2
* *** * * **
**** * * *
** **
=
**
∨
** **
∨
****
1 2
**
3
**
∨
*
**
∨
*
**
1= a
1
a
2
b
1
b
2
∨ a
1
a
2
b
1
b
2
; 3 = a
1
b
1
a
3
b
3
∨ a
1
b
1
a
3
b
2
;
2 = a
2
b
1
b
2
b
3
∨ a
2
b
1
b
2
a
3
∨
a
1
a
2
b
2
b
3
∨ a
1
a
2
b
2
a
3
∨ a
2
b
1
b
2
a
3
∨
∨ a
2
b
1
b
2
b
3
∨ a
1
a
2
b
2
a
3
∨ a
1
a
2
b
2
b
3
;
4 = a
1
a
2
b
2
a
3
b
3
∨ a
2
b
1
b
2
a
3
b
3
∨ a
1
a
2
b
2
a
3
b
3
∨ a
2
b
1
b
2
a
3
b
3
.
4
(1.13.4)
**** **
* *** ** ** * *
*** * **
** ** ** ** * *
c
3
**** **
** ** ** ** * *
****
=
**
∨ ∨
*
** **
1
**
2
**
3
**
∨
** *
***
** * * *
***
∨
** *
*
**
∨
*
∨
**
4 5
*
6
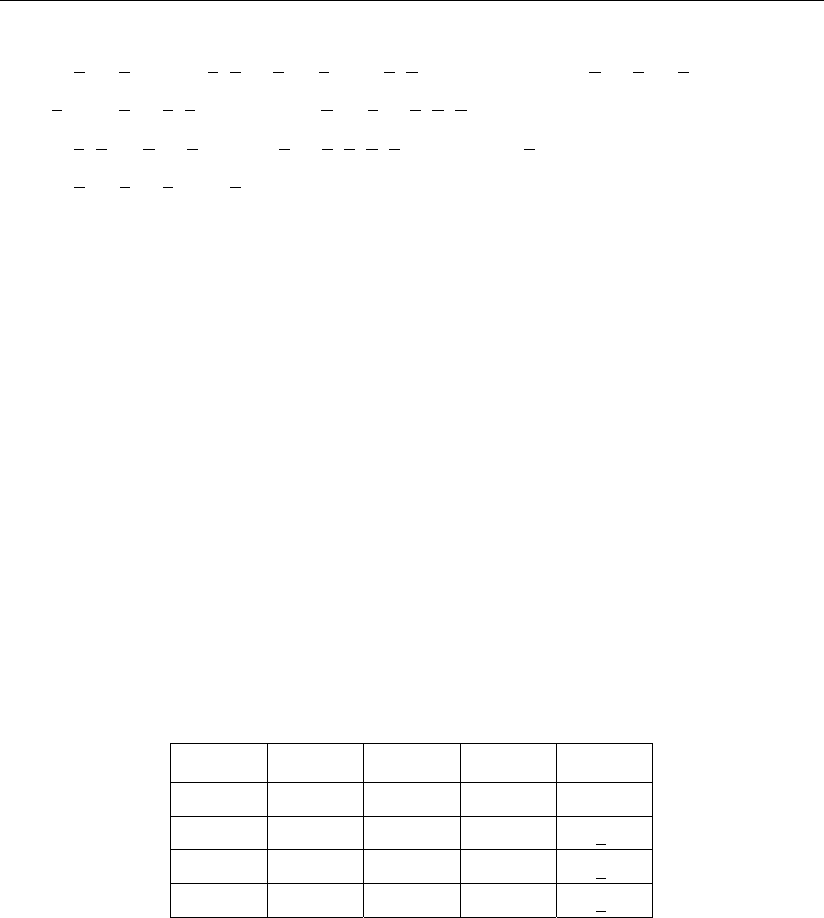
Рис. 1.35
Рис. 1.34
Глава 1
88
1 = a
2
b
2
a
3
b
3
∨ a
2
b
2
a
3
b
3
∨ a
2
b
2
a
3
b
3
∨ a
2
b
2
a
3
b
3
; 2 = a
2
b
1
a
3
b
3
∨ a
2
b
1
a
3
b
3
;
3 = a
1
a
2
b
1
b
3
∨ a
1
a
2
b
1
b
3
; 4 = a
2
b
1
b
2
a
3
∨ a
2
b
1
b
2
a
3
;
5 = a
1
a
2
b
2
a
3
b
3
∨ a
1
a
2
b
2
a
3
b
3
∨ a
1
a
2
b
2
a
3
b
3
∨ a
1
a
2
b
2
a
3
b
3
;
6 = a
1
b
1
b
2
a
3
∨ a
1
a
2
b
1
b
3
.
(1.13.5)
Процедура определения геометрических подмножеств, составляющих
множества геометрических образов сигналов c
1
, c
2
,c
3
, представлена в гра-
фическом виде соответственно на рис.1.33 – 1.35. Эти геометрические под-
множества в каждом основном множестве изображены на рисунках для
большей прозрачности записи их логических выражений отдельными под-
группами, логические зависимости для которых приведены ниже рисунков
и обозначены курсивом цифрами красного цвета. Логические суммы этих
подмножеств и определяют схемное выполнение основного логического
блока сумматора, а режимы работы сумматора при переходе от суммирова-
ния к вычитанию меняются также в зависимости от сигналов заема и пере-
носа P
n–1
(Z
n–1
) и реализуются соответствующим инвертированием сигналов
операндов и выходного сигнала c
3
по данным таблицы истинности (табл.
1.13.1), в которой режим работы логический нуль (0*) определяет операцию
суммирования C = (A + B), а логическая единица (1*) – операцию вычита-
ния C = (A – B).
Таблица 1.13.1
Режим P
n–1
(Z
n–1
)
A B
c
3
0* 0*
A
B
•
c
3
0* 1*
A
•
B
c
3
1* 0*
A
•
B
c
3
1* 1*
A
B
•
c
3
1.14. Синтез одноразрядных умножителей
Для синтеза одноразрядных умножителей больших оснований систем
счисления необходимо использовать таблицы умножения в цифровых коорди-
натах его операндов. Построение таких одноразрядных умножителей для осно-
ваний систем счисления, кратных двум, даже когда в операндах применяется
основной двоичный код, исследовано недостаточно, а синтез систем счисления
таких оснований при нетрадиционных двоичных кодах, необходимость приме-
нения которых возникает в цифровых системах с обнаружением и исправлени-
Основные положения теории
89
ем различного типа ошибок, в литературе отсутствует. Это положение можно
объяснить тем, что нетрадиционные двоичные коды до настоящего времени
считались непригодными для выполнения любых арифметических операций.
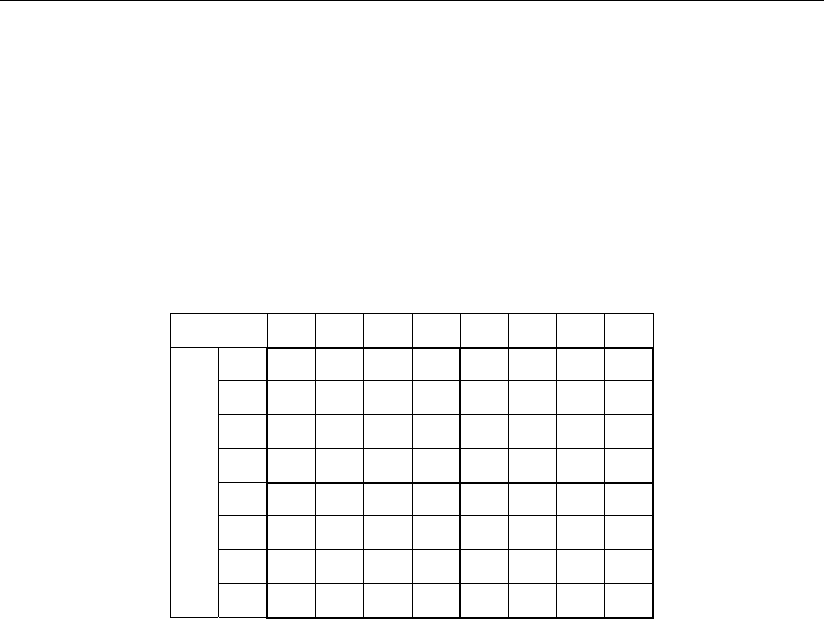
На примере табл. 1.14.1 системы счисления основания n = 8 проведем син-
тез одноразрядного умножителя C = A × B, когда его операнды и выходные
сигналы представляются в различных комбинациях их кодов на входных и вы-
ходных шинах одноразрядного умножителя.
Таблица 1.14.1
C = A×B
A 0 1 2 3 4 5 6 7
0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
2
0.0 0.2 0.4 0.6 1.0 1.2 1.4 1.6
3
0.0 0.3 0.6 1.1 1.4 1.7 2.2 2.5
4
0.0 0.4 1.0 1.4 2.0 2.4 3.0 3.4
5
0.0 0.5 1.2 1.7 2.4 3.1 3.6 4.3
6
0.0 0.6 1.4 2.2 3.0 3.6 4.4 5.2
B
7
0.0 0.7 1.6 2.5 3.4 4.3 5.2 6.1
Результат операции умножения представляется в этой таблице двухраз-
рядным числом, где цифры первого разряда числа определяют выходной сигнал
конкретного разряда основания системы счисления, а цифры второго разряда –
сигнал переноса в следующий старший разряд. Последующий порядок синтеза
геометрических образов выходных сигналов разрядов c
1
, c
2
,c
3
и сигналов пере-
носа P
1
,
P
2
, P
3
, который основывается на данных табл. 1.14.1, полностью анало-
гичен синтезу устройства сложения. Поэтому, опуская очевидные из вышеиз-
ложенного промежуточные преобразования, на рис. 1.36, а – г приведены гео-
метрические образы этих сигналов соответственно для следующих вариантов
применения кодов в операндах и выходных сигналах устройства:
а) A, B, C – в основном двоичном коде;
б) A, B, C – в коде Грея;
в) A, B – в коде Грея, C – в основном двоичном коде;
г) A – в коде Грея, B и C – в основном двоичном коде.
