Kline R.B. Principles and Practice of Structural Equation Modeling

Подождите немного. Документ загружается.

314 ADVANCED TECHNIQuES, AVOIDING MISTAKES

that is statistically signiﬁcant is that for the direct effect of family status on the IS fac-

tor. This unstandardized coefﬁcients equals –.377, and the corresponding standardized

coefﬁcient equals –.244. Thus, adolescents with higher scores on the family status vari-

able have lower initial levels of alcohol use, when we adjust for measurement error and

control for gender. Because this variable is coded 0 = single-parent family and 1 = two-

parent family, we can say that adolescents who live with two parents have lower initial

levels of drinking by .244 standard deviations compared with adolescents who live with

only one parent. The unstandardized coefﬁcient for the direct effect of gender on the

LC factor, or .065, is not statistically signiﬁcant. However, the standardized estimate for

this path, or .166, is nearly as large in absolute value as that for the direct effect of family

status on the IF factor, so here we will not ignore the former result. Because gender is

coded as 0 = male and 1 = female, this result indicates that the rates of linear increase in

alcohol use over time were generally greater for female than for male adolescents.

The predicted means on the alcohol use indicators for the prediction model calcu-

lated by Mplus and their observed (sample) counterparts are as follows:

Indicator Observed Predicted

Year 1 2.271 2.291

Year 2 2.560 2.511

Year 3 2.694 2.732

Year 4 2.965 2.953

These predicted means are very similar to the corresponding observed means. Values

of the predicted means just listed can also be calculated by hand using the tracing rule,

but doing so is more complicated for the prediction model of Figure 11.3 than for the

ﬁnal change model. This is because the total effect of the constant on each indicator in

the prediction model is made up of six different indirect effects through the predictors

(gender, family status) and both latent growth factors. Fortunately, many SEM computer

programs that analyze means can automatically calculate predicted means of endog-

enous variables. You can download from this book’s website (see p. 3) the Mplus and

EQS computer ﬁles for analysis of the prediction model in Figure 11.3.

extensions of latent growth Models

The basic framework for univariate growth curve modeling in a single sample just

discussed can be extended in many ways. For example, the predictors in the empiri-

cal example (gender, family status) are time-invariant predictors in that they were

measured only once. It is also possible to include time-varying predictors that are

themselves repeated measures variables, typically measured at the same intervals as the

indicators of the latent growth factors (e.g., Kaplan, 2009, chap. 8). Each predictor in

the empirical example was represented as an error-free single indicator (e.g., see Figure

11.3). Given a priori estimates of error variance for observed predictors in an LGM, one

could use the method described in Chapter 10 to take account of measurement error in

Mean Structures and Latent Growth Models 315

single indicators (e.g., Figure 10.4(a)). Another way to control for measurement error is

to use multiple indicators of an exogenous factor speciﬁed to predict the latent growth

factors. That is, the prediction part of an LGM can be fully latent. The capability to

represent latent variables as predictors in an LGM distinguishes SEM from HLM, which

features no direct way to do so. It also possible to estimate in SEM indirect effects among

the predictors of latent growth factors, but doing so in HLM is difﬁcult. Even another

variation that is possible in SEM is the analysis of an LGM where the repeated measures

variables are all latent, each measured with multiple indicators.

It may also be possible within the limits of identiﬁcation to specify that some load-

ings on a latent change factor as free parameters. One strategy to do so was described

by Meredith and Tisak (1990) and referred to as nonlinear curve ﬁtting by Kaplan

(2009). In this approach for the empirical example, one would ﬁx the loading of the Year

1 report of alcohol use on a slope factor to zero in order to estimate the intercept, ﬁx the

loading of the Year 2 report to 1 in order to scale this factor, and let the remaining two

loadings be freely estimated. This tactic results in what is basically an empirical devel-

opmental function that optimally ﬁts the slope factor to the data in a particular sample.

Ratios of freely estimated loadings on the slope factor can also be formed to compare

rates of development at different points in time. For instance, if the relative increases in

the freely estimated loadings on the slope factor are not constant over time, the overall

pattern of change may be curvilinear.

It is possible to analyze multivariate latent growth models of change across two

or more domains. If these domains are measured at the same points in time, then the

model reﬂects a parallel growth process (Kaplan, 2009). For example, George (2006)

analyzed data from a longitudinal annual survey of students from Grade 7 to Grade

11 about their interest in science classes and attitudes about the utility of science in

everyday life. George (2006) evaluated a model of cross-domain change in which the

within-domain latent growth factors were allowed to covary across the domains. The

results indicated that while students’ interest in science courses steadily declines during

the middle school and high school years, their views of science utility generally increase

over the same time. Higher initial interest in science classes predicted a more posi-

tive attitude about science utility, and changes in one domain covaried positively with

changes in the other domain. Furthermore, initial levels in each of these domains were

negatively associated with change in the other domain. For example, students who in

Grade 7 expressed more positive attitudes about science utility exhibited a more gradual

decline in their interest in science classes from Grade 7 to 11.

Like just about any other kind of structural equation model, an LGM can be ana-

lyzed across multiple samples. For example, Benyamini, Ein-Dor, Ginzburg, and Solo-

mon (2009) studied the impact of combat stress and posttraumatic stress symptoms

on the level and growth trajectories of self-reported health among Israeli veterans of

the 1982 Lebanon War who were tested at 1, 2, 3, and 20 years after the conﬂict. The

veterans were divided into two groups, one diagnosed as exhibiting a combat stress

reaction (CSR) during the war and a matched control group without this diagnosis but

exposed to similar combat experiences. The CSR group showed poorer initial levels of

316 ADVANCED TECHNIQuES, AVOIDING MISTAKES

self-reported health status. The trajectory of these veterans was positive over time (they

improved), but their levels of self-reported health remained lower than that of the con-

trol group. Also, the experience of posttraumatic stress symptoms in the ﬁrst few years

after the war slowed the rate of subsequent improvement within the CSR group.

Bollen and Curran (2004) describe a class of models they refer to as autoregres-

sive latent trajectory (ALT) models in which the indicators of latent growth factors are

allowed to have direct and indirect effects on each other over time. An autoregressive

structure is one where past values of a variable are used to predict future values of that

same variable. That is, lagged (prior) variables are speciﬁed as the predictors of later

measurements on the same variable. For example, the speciﬁcation for the empirical

example presented next

Year 1 → Year 2 → Year 3 → Year 4

illustrates an autoregressive model of one lag where the prior level of reported alcohol

use has a direct effect on the current one. This model implies indirect effects, too, such

as the impact of Year 1 on Year 3 through the mediator Year 2. There are many statis-

tical techniques for analyzing autoregressive structures, including the autoregressive

integrative moving average (ARIMA) model, which uses shifts and lags in a time series

to uncover patterns, such as seasonal trends or various kinds of intervention effects.

In contrast, a standard LGM does not incorporate lagged effects among the indicators.

Instead, indicators are assumed to be spuriously associated due to common causes, in

this case the latent growth factors (e.g., Figure 11.2). Bollen and Curran (2004) argue

that this assumption is unrealistic for certain types of data. They describe an ALT model

as a kind of LGM that includes direct and indirect effects among the indicators. The

basic logic of an ALT model can be extended to analysis of panel data from a series of

one or more repeated measures variables.

struCtured Means In MeasureMent Models

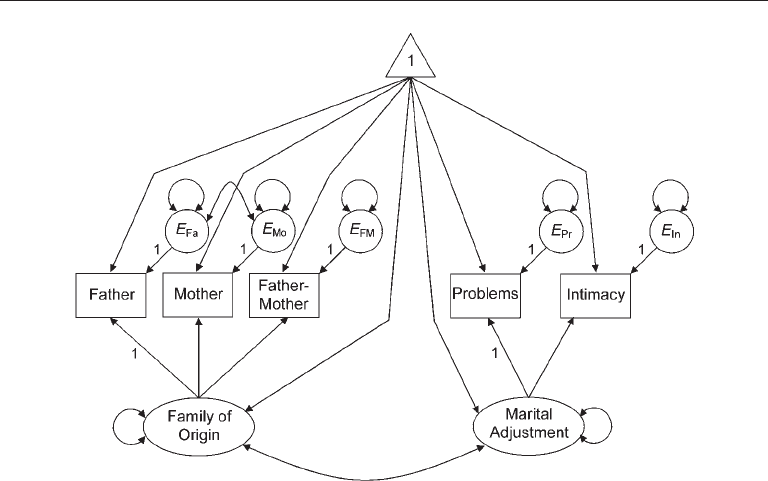
A standard CFA model assumes that the means of all variables are zero. However, it is

possible to add a mean structure to a measurement model. An example is presented

in Figure 11.4. This model’s covariance structure is the measurement model of family-

of-origin experiences (FOE) and marital adjustment evaluated in Chapter 9 with data

collected by Sabatelli and Bartle–Haring (2003) in samples of husbands and wives. The

model in Figure 11.4 also has a mean structure that includes the indicators and the fac-

tors. Based on the principles described earlier, the unstandardized path coefﬁcients for

the regression of the exogenous factors on the constant should theoretically equal the

factor means. Because the indicators are endogenous, (1) the unstandardized coefﬁ-

cients for the direct effects of the constant on the indicators should equal the intercepts

for the regressions of the indicators on the factors, and (2) the indicator means should

be estimated by the total effect of the constant on each indicator.

Mean Structures and Latent Growth Models 317

The model of Figure 11.4 is not identiﬁed if it was estimated with data from a

single sample. This is because its mean structure would be underidentiﬁed: there are

ﬁve observations (means of the ﬁve indicators), but the mean structure has seven param-

eters, including the means of the two factors and the intercepts of the ﬁve indicators. But

if a measurement model with structured means is analyzed across multiple groups and

constraints are imposed on certain parameter estimates, the model can be identiﬁed. A

two-part strategy by Sörbom (1974) to analyze such a model is described next:

1. Fix the factor means to zero in one group, which is the same as constraining

the direct effect of the constant on all factors to zero in that group. These constraints

establish that group as the reference sample. The factor means are then freely estimated

in all other groups, and their values are relative differences on the factors. Suppose that

there is a treatment group and a control group. The latter is the reference sample. If the

direct effect of the constant on a factor in the treatment group is –5.00, then the factor

mean in the treatment group is 5 points higher than in the control group.

2. In order to reasonably estimate relative group differences on factor means, it

must be assumed that the factors are deﬁned the same way in both samples. One way

to address this requirement is to scale the factors the same way by ﬁxing the loadings

of the same indicators (reference variables) to 1.0 across the groups. This tactic is rec-

ommended for multiple-sample CFA regardless of whether means are estimated (Chap-

ter 9). Little, Slegers, and Card (2006) describe other options for scaling the factors in

multiple-sample analyses of models with mean structures. The second way is to test for

FIgure 11.4. A measurement model of family-of-origin experiences and marital adjustment

with a mean structure evaluated across samples of husbands and wives.

318 ADVANCED TECHNIQuES, AVOIDING MISTAKES

measurement invariance across the groups. Speciﬁcally, there should be evidence for at

least partial measurement invariance concerning the factor loadings and indicator inter-

cepts. Without such evidence, there is little point in interpreting group mean differences

on latent variables that are not measured the same way across the groups.

A strategy for testing measurement invariance is suggested next. First, test the equal

form hypothesis, H

form

, by freely estimating all model parameters, including those of

the mean structure, in each group. If this model is rejected, then there is no basis for

invariance at any level and thus none for interpreting factor mean differences. Other-

wise, next test the stronger hypothesis of equal factor loadings and intercepts, H

Λ, τ

, by

imposing cross-group equality constraints on the unstandardized estimates of each fac-

tor loading and indicator intercept. Compare this model using the chi-square difference

test with the less restricted model that corresponds to H

form

. If H

Λ, τ

does not hold for a

couple of indicators, then their factor loadings or intercepts can be estimated separately

within each group (i.e., release the equality constraints on those parameters). This con-

trols for unequal loadings or intercepts for regressions of the indicators on the factors

across the groups. However, if none of the loadings or intercepts are equal across the

groups—that is, H

form

is the only retained invariance hypothesis—there are no grounds

for interpreting factor mean contrasts.

empirical example

In Chapter 9, we determined in a multiple-sample CFA across samples of husbands

and wives that the measurement model only in Figure 11.4 is invariant concerning the

unstandardized factor loadings and measurement error variances. However, it was nec-

essary to freely estimate in each sample the factor variances and covariance and the

error covariance between the mother and father indicators of the FOE factor (Tables

9.9–9.10). In this analysis, the mean structure illustrated in Figure 11.4 was added to

the measurement model just described. The husbands are the reference sample, so the

direct effects of the constant on both factors (the factor means) were constrained to

equal zero in this group. In contrast, these two parameters were freely estimated in the

sample of wives, and their unstandardized values estimate relative mean differences

between wives and husbands on each factor. The direct effects of the constant on each

indicator (the intercepts) were constrained to be equal for husbands and wives. This set

of cross-group equality constraints (ﬁve in total) tests the hypothesis of equal intercepts

for regressions of indicators on the factors. With ﬁve indicators in each sample, the total

number of observations is 5(8)/2 × 2, or 40. The total number of free parameters is 23.

This includes (1) 13 parameters constrained to be equal for husbands and wives (ﬁve

indicator intercepts, ﬁve measurement error variances, and three factor loadings); (2)

four parameters freely estimated within each sample (three factor variances and covari-

A variation is to test invariance of factors loadings and intercepts over two separate steps.

Mean Structures and Latent Growth Models 319

ance and one error covariance) for a total of eight altogether; and (3) two factor mean

differences estimated only for wives. Thus, df

= 40 – 23 = 17.

The measurement model with structured means just described was simultaneously

ﬁtted using the ML method in EQS 6.1 to the covariance matrices and means based on

the data summarized in Table 9.8 for husbands and wives. The default iteration limit of

30 in EQS was increased to 200 for this relatively complex analysis. The initial run in

EQS terminated with two types of error messages. First, the program “complained” of

bad start values in the initial iterations. Second, the program issued “condition codes”

for three different parameters, which means that EQS was unable to calculate “proper”

(admissible) estimates of these parameters without imposing inequality constraints. The

problematic parameters ﬂagged by EQS included the variance of the marital adjustment

factor, the error variance of the intimacy indicator of the same factor, and the factor

loading of this indicator (see Figure 11.4).

To deal with these problems, I speciﬁed in a second run with EQS start values for

the parameters just mentioned. I took these values from the ﬁnal measurement model

for husbands and wives estimated in Chapter 9 (Table 9.10). In the second analysis with

these start values, EQS issued a warning (not error) message about bad start values

in the ﬁrst iteration and another message about a parameter matrix that may be non-

positive in the second through fourth iterations, but the program went on to generate a

converged and admissible solution. You can download the EQS syntax and output ﬁles

for this analysis from this book’s website (p. 3). The syntax ﬁle includes speciﬁcation of

the start values for the second analysis. Reported next are values of selected ﬁt statistics

calculated by EQS for the covariance structure only; the 90% conﬁdence interval based

on the RMSEA is reported in parentheses:

(17) = 13.599, p = .695

RMSEA = 0 (0–.033)

GFI = .986; CFI = 1.000; SRMR = .027

All absolute correlation residuals were < .10 for both the husbands and wives. The EQS

program also printed a value of the RMSEA and its 90% conﬁdence interval based on the

covariances and means (i.e., the whole model of Figure 11.4), and the results are RMSEA

= 0 (0–.070). We will see later in this chapter that the predicted means are similar to the

observed means in both samples. Finally, none of the standardized residuals (calculated

in LISREL) were statistically signiﬁcant for either husbands or wives. Given all these

results, the model in Figure 11.4 with equality-constrained factor loadings, indicator

error variances, and intercepts was retained. You can download from this book’s website

(p. 3) all EQS, LISREL, and Mplus computer ﬁles for this analysis.

Reported in Table 11.7 are ML parameter estimates for the measurement model of

Figure 11.4. These estimates are similar, but not identical, to those presented in Table

9.10 for the multiple-sample CFA with no mean structure. The two sets of parameter

estimates are not identical because the mean structure in Figure 11.4 was estimated

320 ADVANCED TECHNIQuES, AVOIDING MISTAKES

with cross-group equality constraints imposed on the indicator intercepts. However, the

results in Table 11.7 for the measurement model are so close to those in Table 9.10 that

no new interpretation is needed.

Presented in the top part of Table 11.8 are the unstandardized estimates of the

direct effects of the constant on the factors calculated for wives only. They are inter-

preted as estimated factor mean differences between husbands and wives adjusted for

measurement error. The result for the FOE factor is 3.196, indicating that the mean score

for wives on this factor is predicted to be about 3.2 points higher than that for husbands.

That is, wives generally report more positive FOE experiences than their husbands. The

estimated standard error for this factor mean difference is 1.643. In a large sample—and

if we assume normality and homogeneity of variance—the ratio 3.196/1.643 = 1.95 is

interpreted as a z test of whether the estimated factor mean contrast differs statistically

from zero. The positive two-tailed critical value of z at the .05 level is 1.96. Thus, the

taBle 11.7. Maximum likelihood Parameter estimates for the Covariance

structure of a two-Factor Model of Family-of-origin experiences and Marital

adjustment with structured Means analyzed across samples of husbands and

Wives

Husbands Wives

Parameter Unst.

St. Unst.

St.

Unconstrained estimates

Factor variances and covariance

FOE

85.654 20.474 1.000 139.199 29.405 1.000

Mar Adj

459.106 106.661 1.000 595.685 149.121 1.000

FOE Mar Adj

95.053 28.249 .479 140.477 40.883 .488

Measurement error covariance

−8.925

14.293 −.161 20.781

14.442 .374

Equality-constrained estimates

Factor loadings

Mar Adj → Probs

1.000

— .688 1.000

— .734

Mar Adj → Intim

.917 .142 .979 .917 .142 .984

FOE → Father

1.000

— .828 1.000

— .883

FOE → Mother

.859 .078 .668 .859 .078 .753

FOE → Fa-Mo

.932 .139 .663 .932 .139 .749

Measurement error variances

510.316 89.025 .526 510.316 80.025 .461

16.757

61.705 .042 16.757

61.705 .032

39.421

15.789 .315 39.421

15.789 .221

78.371 15.438 .554 78.371 15.438 .433

Fa-Mo

94.944 16.096 .560 94.944 16.096 .440

Note. Unst., unstandardized; St., standardized; FOE, family-of-origin experiences. Standardized estimates for

measurement errors are proportions of unexplained variance.

p ≥ .05;

not tested for statistical signiﬁcance;

p < .05. For all other unstandardized estimates, p < .01.

Mean Structures and Latent Growth Models 321

estimated mean difference between wives and husbands of about 3.2 points on the FOE

factor falls just short of statistical signiﬁcance at the .05 level. However, the group size

for this analysis is not large (n = 103), and the factor variances were estimated separately

for wives and husbands, so the homogeneity of variance assumption may not hold. This

means that the p value for this z test may not be very accurate. The estimated mean

difference on the marital adjustment factor is .665 and is not close to being statistically

signiﬁcant because the ratio of this difference over its standard error is z = .665/3.275

= .203.

Reported in the bottom part of Table 11.8 are the estimates of intercepts for regres-

sions of the indicators on the factors when equal values are assumed for husbands and

wives. Because the direct effects of the constant on both factors are constrained to zero

for the husbands, the constant has no indirect effects on the indicators through the fac-

tors in this group. Thus, (1) the total effects of the constant on the indicators consist

of direct effects only, and (2) these total effects are the model-implied means of the

indicators for the husbands. However, the intercepts for the wives reported in Table 11.8

are not also predicted means. Because the constant has direct effects on the factors for

wives, it has both direct and indirect effects on the indicators in this group. Thus, it is

the total effects of the constant on the indicators that equal the model-implied means of

the indicators for the wives. Presented in Table 11.9 are the predicted indicator means

automatically calculated by EQS and also the observed means for husbands and wives.

taBle 11.8. Maximum likelihood Parameter estimates for the Mean structure

of a two-Factor Model of Family-of-origin experiences and Marital adjustment

with structured Means analyzed across samples of husbands and Wives

Husbands Wives

Parameter Unstandardized SE Unstandardized SE

Estimated for wives only

Factor means

→ FOE

0 — 3.196

1.643

→ Mar Adj

0 — .665

3.275

Equality-constrained estimates

Indicator intercepts

→ Probs

158.330 2.664 158.330 2.664

→ Intim

137.871 1.987 137.871 1.987

→ Father

83.079 1.055 83.079 1.055

→ Mother

84.493 1.009 84.493 1.009

→ Fa-Mo

81.535 1.153 81.535 1.153

Note. FOE, family-of-origin experiences. All standardized estimates are zero.

p ≥ .05. For all other unstandardized estimates, p < .01.

322 ADVANCED TECHNIQuES, AVOIDING MISTAKES

Each predicted mean is generally similar to the corresponding observed mean in both

samples.

For an example of the analysis of measurement models with means over time

instead of groups, see Contrada, Boulifard, Idler, Krause, and Labouvie (2006), who

estimated changes in factor means in a longitudinal study of depression among heart

surgery patients.

sr Models with structured Means

The analysis of an SR model with a mean structure over multiple groups follows the

same basic rationale as for a CFA model with a mean structure. For example, factor mea-

surement should be speciﬁed the same way in all groups. For the group selected as the

reference sample, all direct effects of the constant on the factors are ﬁxed to zero in order

to identify the mean structure. A notable difference is that direct effects of the constant

on endogenous factors are interpreted as relative group differences in the intercepts for

the regression of those factors on other variables speciﬁed as direct causes, such as exog-

enous factors. Because of different identiﬁcation requirements for an LGM, it is possible

to estimate the means and intercepts of latent growth factors in a single sample. This

implies that these same parameters can be estimated separately for each group when an

LGM is simultaneously analyzed across multiple samples.

MIMIC Models as an alternatIve

to MultIPle-saMPle analYsIs

Another way to estimate group differences on latent variables is through the speciﬁca-

tion of a MIMIC model where factors with effect indicators are regressed on one or more

dichotomous cause indicators that represent group membership. The total sample in

taBle 11.9. observed and Predicted Means for a two-Factor Model of Family-

of-origin experiences and Marital adjustment with structured Means analyzed

across samples of husbands and Wives

Husbands Wives

Indicator Observed Predicted Observed Predicted

Marital adjustment indicators

Problems

155.547

158.330 161.779 158.996

Intimacy

137.971

137.871 138.382 138.482

Family-of-origin experiences indicators

Father

82.764

83.079 86.229 86.276

Mother

85.494

84.493 86.392 87.238

Father-Mother

81.003

81.535 85.046 84.514

Mean Structures and Latent Growth Models 323

this approach is not partitioned into subsamples (although subsamples are still required

in the study design). Thus, there are no special identiﬁcation requirements beyond the

usual ones for single-sample analyses for the types of MIMIC models described next.

However, the MIMIC approach described here assumes measurement invariance across

the groups. Indeed, there is no way to test this assumption in the MIMIC approach to a

multiple-sample analysis.

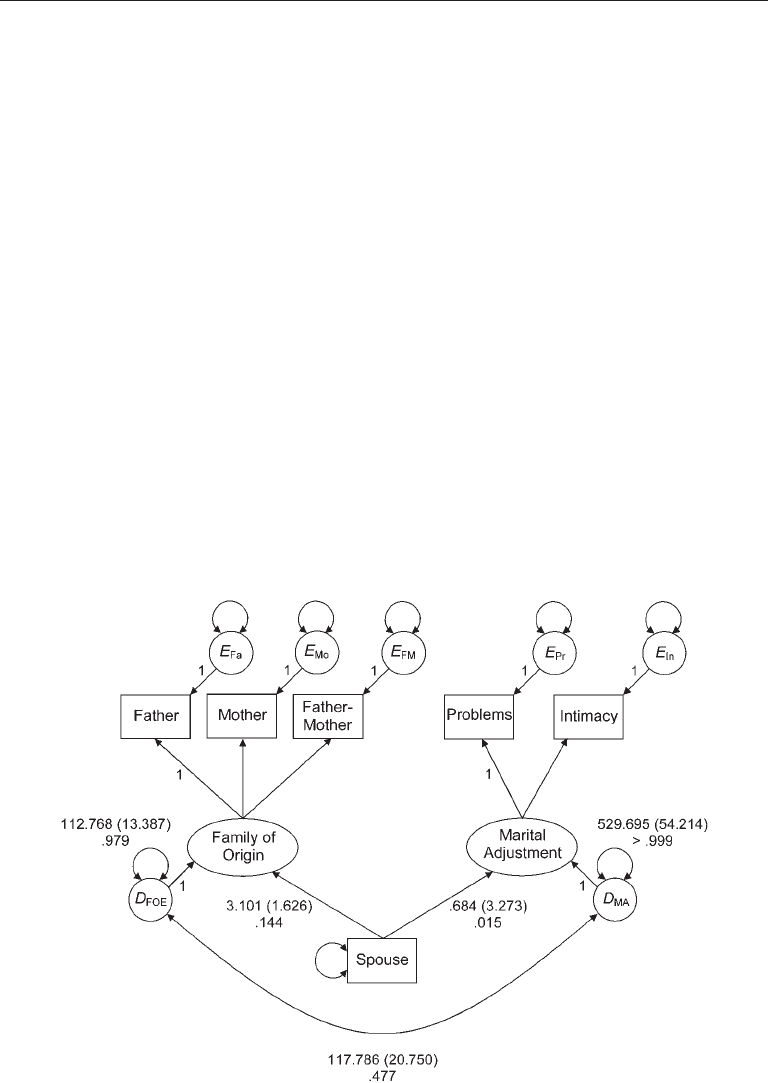
Consider the model in Figure 11.5. It is speciﬁed as a MIMIC alternative to the

model of Figure 11.4, which was analyzed across separate samples of husbands and

wives. The single-cause indicator in the MIMIC model of Figure 11.5 is a dichotomy

that represents the spouse coded as 0 = husband and 1 = wife. This contrast variable is

speciﬁed to have direct effects on an FOE factor with three effect indicators and a mari-

tal adjustment factor with two effect indicators. These are the same factors and indica-

tors as represented in Figure 11.4, but the factors are endogenous in the MIMIC model

of Figure 11.5 and thus have disturbances. These disturbances are allowed to covary,

which reﬂects the assumption that the factors have common omitted causes besides the

difference between husbands and wives. The MIMIC model of Figure 11.5 does not have

a mean structure; instead, it has just a covariance structure. This implies that all means

are assumed to be zero (they are not analyzed). However, the path coefﬁcients for the

FIgure 11.5. A MIMIC (multiple indicators and multiple causes) model of family-of-origin

experiences and marital adjustment evaluated in a single sample with spouse as a cause indicator.

Parameter estimates are reported as unstandardized (standard error) standardized. Standardized

disturbance variances are proportions of unexplained variance.