Kline R.B. Principles and Practice of Structural Equation Modeling

Подождите немного. Документ загружается.

294 CORE TECHNIQuES

recent special issue of the Journal of Business Research (Diamantopoulos, 2008). The edited

volume by Vinzi, Chin, Henseler, and Wang (2009) provides in-depth coverage of the tech-

nique of PLS-PM.

Diamantopoulos, A. (Ed.). (2008). Formative indicators [Special issue]. Journal of Business

Research, 61(12 ).

Howell, R. D., Breivik, E., & Wilcox, J. B. (2007). Reconsidering formative measurement.

Psychological Methods, 12, 205–218.

Vinzi, V. E., Chin, W. W., Henseler, J., & Wang, H. (2009). (Eds.). Handbook of partial least

squares: Concepts, methods and applications in marketing and related ﬁelds. New York:

Springer.

eXerCIses

1. Calculate the rho coefﬁcient for each factor in Figure 10.2 using the parameter

estimates in Tables 10.3 and 10.4.

2. Fit the model in Figure 10.5 and to the data in Table 10.5. Now respecify this

model to take direct account of measurement error in the single indicator of

depression (assume r

= .70) and ﬁt the respeciﬁed model to the same data.

Compare estimates for direct effects on depression (from stress, SES) and also

the disturbance variances for depression across the two analyses. Comment on

the pattern. What is the “surprise” among other estimates?

3. Respecify the formative measurement model in Figure 10.6(b) to take direct

account of measurement error at the indicator level, not the construct level.

4. Critique the model in Figure 10.5 in terms of reﬂective versus formative mea-

surement.

5. Calculate a standardized effect decomposition for the structural model in Fig-

ure 10.3.

6. Show that df

= 47 for the measurement model in Figure 10.2.

7. Look through the EQS or LISREL output ﬁles for the analysis of the ﬁnal

Houghton–Jinkerson SR model (its structural model is shown in Figure 10.3)

and in particular at the sections about effect decomposition. Besides effects of

factors on other factors, what else do you notice in the decomposition?

295

APPENDIX 10.A

Constraint Interaction in SR Models

Recall that constraint interaction for CFA models is indicated when the value of the chi-square

difference (

) statistic for the test of the equality of the loadings of indicators for different fac-

tors depends on how the factors are scaled (Appendix 9.B). Steiger (2002) shows that the same

phenomenon can happen with SR models where some factors have only two indicators and when

estimates of direct effects on two or more different endogenous factors are constrained to be equal.

Constraint interaction can also result in an incorrect standardized solution for an SR model if it is

calculated in the way described earlier (in two steps).

The presence of constraint interaction can be detected the same way for SR and CFA mod-

els: while imposing the equality constraint, change the value of each identiﬁcation constraint for

the factors from 1.0 to another positive constant and rerun the analysis. If the value of the model

chi square

changes by an amount that exceeds what is expected by rounding error, there is

constraint interaction. Steiger (2002) suggests a way to deal with constraint interaction in SR

models: if the analysis of standardized factors can be justiﬁed, the method of constrained estima-

tion can be used to test hypotheses of equal standardized path coefﬁcients and to generate correct

standard errors. Constrained estimation of an SR model standardizes all factors, exogenous and

endogenous.

Part III

Advanced Techniques,

Avoiding Mistakes

299

Mean Structures and Latent Growth

Models

The basic datum of SEM, the covariance, does not convey information about means.

If only covariances are analyzed, then all observed variables are effectively mean-

deviated (centered) so that substantive latent variables must have means of zero.

Sometimes this loss of information is too restrictive, such as when means of repeated

measures variables are expected to differ. Means are estimated in SEM by adding a

mean structure to the model’s basic covariance structure (i.e., its measurement or struc-

tural components). The input data for the analysis of a model with a mean structure

are covariances and means (or the raw scores). The SEM approach to the analysis of

means is distinguished by the capability to test hypotheses about means of substantive

latent variables and the error covariance structure. The analysis of latent growth models

and the multiple-sample analysis of measurement models with structured means are

also considered.

logIC oF Mean struCtures

The technique of multiple regression (MR) provides the basic logic for analyzing covari-

ance structures in SEM. It provides the rationale for analyzing means, too. Recall that

unstandardized regression equations have both a covariance structure (B

weights) and

a mean structure in the form of the intercept (A) (Equation 2.1). For example, consider

the scores on variables X and Y presented in Table 11.1. The unstandardized equation for

predicting Y from X for these data is

= .455 X + 20.000

The regression coefﬁcient, .455, conveys no information about the mean of either vari-

able. The intercept, 20.000, reﬂects the mean of both variables and the regression coef-

300 ADVANCED TECHNIQuES, AVOIDING MISTAKES

ﬁcient, albeit with a single number. Given M

= 11.000 and M

= 25.000 (Table 11.1), the

intercept can be expressed according to Equation 2.5 as

A = 25.000 – .455 (11.000) = 20.000

Likewise, the mean of Y can be expressed as a function of the intercept, regression coef-

ﬁcient, and mean of X, as follows:

= 20.000 + .455 (11.000) = 25.000

How a computer calculates the intercept of an unstandardized regression equation

provides the key to understanding the analysis of means in SEM. Look again at Table

11.1 and in particular at the column labeled

, which represents a constant that equals

1 for every case in this application of the McArdle–McDonald symbolism for SEM. Sum-

marized in Table 11.2 are the results of two regression analyses with the constant. Both

analyses were conducted by instructing the computer to omit from the analysis the

intercept term it would otherwise automatically calculate. (This is an option in most

regression modules.) In the ﬁrst analysis, Y is regressed on both X and the constant.

Note that the regression coefﬁcient for X is the same as before, .455, and for the con-

taBle 11.1. example Bivariate data set

Raw scores Constant

Case X Y

3 24 1

8 20 1

10 22 1

15 32 1

19 27 1

11.000 25.000 —

6.205 4.690 —

38.500 22.000 —

Note. r

= .601.

taBle 11.2. results of regression analyses with a

Constant for the data in table 11.1

Regression Predictor(s)

Unstandardized

coefﬁcient(s)

1. Y on X and

.455

20.000

2. X on

11.000

Mean Structures and Latent Growth Models 301

stant it is 20.000, which is the intercept. The second analysis in Table 11.2 concerns the

regression of X on the constant. The regression coefﬁcient in this analysis is 11.000, or

the mean of X. These results illustrate two principles about mean structures:

When a criterion is regressed on a predictor and a constant, the (Rule 11.1)

unstandardized coefﬁcient for the constant is the intercept.

When a predictor is regressed on a constant, the unstandardized (Rule 11.2)

coefﬁcient is the mean of the predictor.

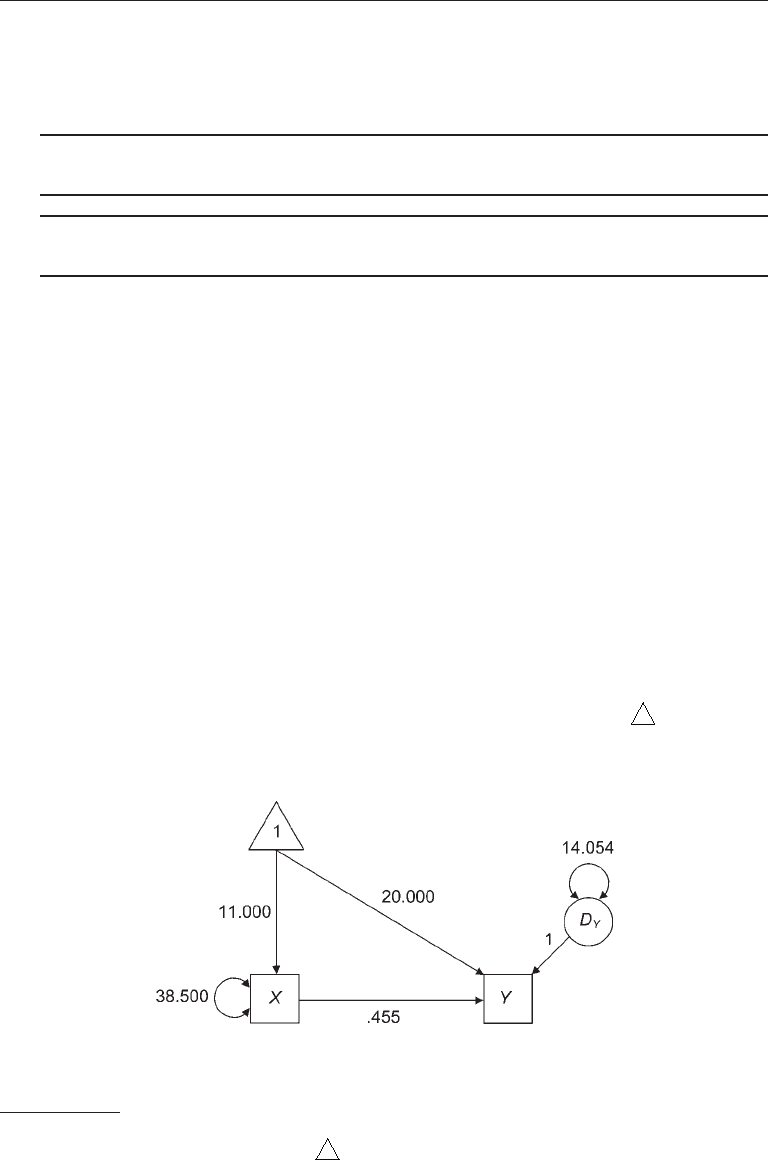
A path analytic representation of the regression analyses just described is presented

in Figure 11.1. Unlike a standard path model, the one in the ﬁgure has both a covariance

structure and a mean structure. The covariance structure includes the direct effects of

the measured and unmeasured exogenous variables (respectively, X and D) and their

variances. Estimating this covariance structure with the data in Table 11.1 using stan-

dard regression (OLS estimation) yields an unstandardized path coefﬁcient of .455—

the same as the unstandardized regression coefﬁcient—and a disturbance variance of

14.054.

No information about the means is represented in this covariance structure.

The mean structure in Figure 11.1 consists of direct effects of the constant on both

observed variables. Although the constant is depicted as exogenous in the ﬁgure, it is not

an exogenous “variable” in the usual sense because it has no variance. The unstandard-

ized path coefﬁcient for the direct effect of the constant on the predictor X is 11.000, or

the mean of X, just as in the corresponding regression analysis (Table 11.2). The mean

of X is thus explicitly represented in the mean structure of the path model in the form

of an unstandardized path coefﬁcient.

Because the constant has no indirect effect on

X through other variables, the unstandardized coefﬁcient for the path

→ X is also

the total effect. The unstandardized path coefﬁcient for the direct effect of the constant

This error variance is calculated in OLS estimation as (1 –

)

= (1 – .601

) 22.000 = 14.054.

The standardized coefﬁcient for the path

→ X is zero because the means of standardized variables

are zero.

FIgure 11.1. A path model with a mean structure.

302 ADVANCED TECHNIQuES, AVOIDING MISTAKES

on the endogenous variable Y is 20.000, which is the intercept. In addition to this direct

effect, the constant also has an indirect effect on Y through X. Using the tracing rule for

this model, we obtain this result:

Total effect of

on Y = Direct effect + Indirect effect

= 20.000 + .455 (11.000) = 25.000

which equals the mean of Y. Two additional principles about mean structures can thus

be expressed in path analytic language:

The mean of an endogenous variable Y is a function of three (Rule 11.3)

parameters—(1) the intercept, (2) the unstandardized path

coefﬁcient(s), and (3) the mean(s) of the exogenous variable(s).

The model-implied (predicted) mean for an observed variable is the (Rule 11.4)

total effect of the constant on that variable.

Because the mean structure of the model in Figure 11.1 is just-identiﬁed (i.e., two

observed means, two direct effects of

), the predicted means for X and Y equal their

observed counterparts. This fact is elaborated next.

When an SEM computer tool analyzes means, it automatically creates a constant on

which variables in the model are regressed. A variable is included in the mean structure

by specifying that the constant has a total effect on it. This leads to two more prin-

ciples:

For exogenous variables, the unstandardized path coefﬁcient for the (Rule 11.5)

direct effect of the constant is a mean.

For endogenous variables, though, the direct effect of the constant (Rule 11.6)

is an intercept but the total effect is a mean.

If a variable is excluded from the mean structure, the mean of that variable is assumed to

be zero. Residual terms (disturbances, measurement errors) are never included in mean

structures because their means are assumed to be zero. In fact, the mean structure may

not be identiﬁed if the mean of an error term is inadvertently speciﬁed as a free param-

eter. Three points warrant special mention:

1. There is no standard symbol in the SEM literature for mean structures. The

symbol

is used in diagrams here mainly as a pedagogical device so that you quickly

recognize the presence of a mean structure and determine which variables it includes.

But it is not absolutely necessary to explicitly represent mean structures in model dia-

grams. Some authors present just the covariance structure in a diagram and report esti-

mates about means in accompanying tables.

Mean Structures and Latent Growth Models 303

2. It is theoretically possible to analyze means of observed variables in a path anal-

ysis, but this is rarely done in practice. It is more common in SEM to estimate means of

latent variables (factors) represented in measurement models.

3. Special forms of maximum likelihood (ML) estimation for raw data ﬁles with

missing observations, including the expectation–maximization (EM) algorithm, esti-

mate both covariances and means. That is, they add a mean structure to the model.

Depending on how these special methods are implemented in a particular SEM com-

puter tool, it may or may not be necessary to explicitly specify a mean structure even if

the original model has only a covariance structure.

IdentIFICatIon oF Mean struCtures

The two principles listed next concern identiﬁcation of mean structures:

The parameters of a model with a mean structure include (1) the (Rule 11.7)

means of the exogenous variables, (2) the intercepts of the

endogenous variables, and (3) the number of parameters in the

covariance portion of the model counted in the usual way for that

type of model.

A simple rule for counting the number of observations available to estimate the param-

eters of a model with both covariance and mean structures is stated next:

If v is the number of observed variables, then the number of (Rule 11.8)

observations equals v (v + 3)/2 when means are analyzed.

The value of the expression in Rule 11.8 gives the total number of variances, nonredun-

dant covariances, and means of observed variables. For instance, if there are three

observed variables, then there are 3(6)/2, or nine observations, including three means,

three variances, and three unique covariances (e.g., see the lower right side of Table

3.2).

In order for a mean structure to be identiﬁed, the number of its parameters can-

not exceed the total number of means of the observed variables. Also, the identiﬁca-

tion status of a mean structure must be considered separately from that of the covari-

ance structure. For example, an overidentiﬁed covariance structure will not identify an

underidentiﬁed mean structure, and vice versa. If the mean structure is just-identiﬁed, it

has as many free parameters as observed means; therefore (1) the model-implied means

(total effects of the constant) will exactly equal the corresponding observed means; and

(2) the ﬁt of the model with just the covariance structure will be identical to that of the

model with both the covariance structure and the mean structure.

For example, the mean structure of the model in Figure 11.1 has two parameters,

→ X and

→ Y (respectively, the mean of X, the intercept when regressing Y on