Кирин Е.М. Метрические задачи в курсе начертательной геометрии

Подождите немного. Документ загружается.

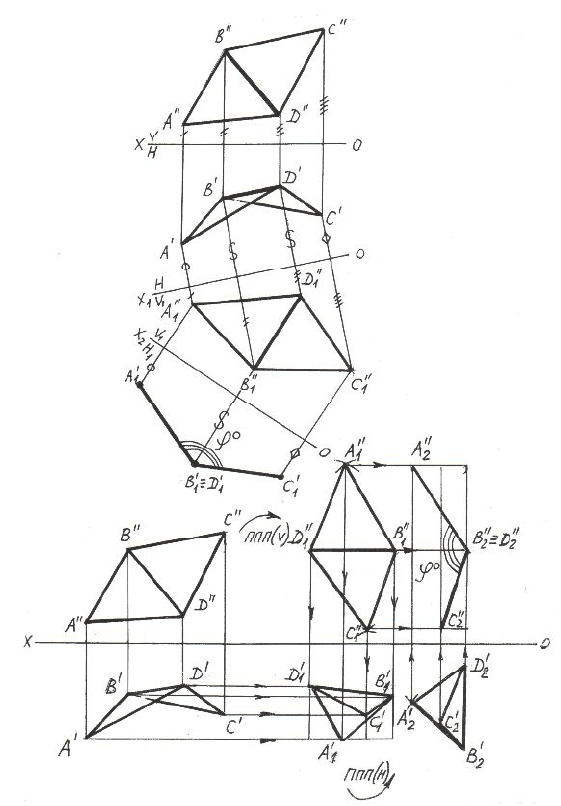
Рисунок 5.10 – Определение двугранного угла методом перемены

плоскостей проекций и плоско-параллельного перемещения

б)

а)

6 МЕТРИЧЕСКИЕ ЗАДАЧИ

НА ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

ЗАДАННЫХ РАЗМЕРОВ И УГЛОВЫХ ВЕЛИЧИН

В предыдущих главах рассматривались метрические задачи, в ко-

торых по метрически искажённым проекциям определялись действи-

тельные размеры геометрических объектов и их угловые величины.

Такие задачи можно назвать прямыми задачами.

Однако в конструкторской практике встречаются задачи, в кото-

рых необходимо построить геометрические объекты с наперёд за-

данными метрическими характеристиками. Такие задачи можно на-

звать обратными метрическими задачами. Рассмотрим несколько об-

ратных метрических задач.

Пример 1. Построить недостающую горизонтальную проекцию

прямой АВ, если её длина равна 50 мм и задана горизонтальная про-

екция точки А.

Задачу решаем методом прямоугольного треугольника (рису-

нок 6.1,а). Из точки А или В на фронтальной проекции строим катет

прямоугольного треугольника. Далее раствором циркуля 50 мм про-

водим дугу и на катете треугольника находим точку В

, которая оп-

ределяет разность ординат концов отрезка АВ. Откладываем найден-

ную разность на горизонтальной проекции и получаем горизонталь-

ную проекцию точки В.

Пример 2. Разделить отрезок АВ в отношении 2:5 (см. рисунок 6.1,б).

Задачу решаем с использованием теоремы Фалеса: если на одной стороне

угла отложить равные или пропорциональные отрезки и провести через

полученные засечки любые параллельные прямые, то они будут отсекать

на другой стороне угла равные или пропорциональные отрезки.

Через любую точку прямой проводим вспомогательную прямую

под любым углом. На вспомогательной прямой откладываем семь

равных произвольной длины отрезков. Конец последнего отрезка со-

единяем с другой точкой прямой. На вспомогательной прямой най-

дём точку K

, которая делит её в заданном отношении. Через взятую

точку проведём линию, параллельную стороне вспомогательного

треугольника, в результате чего получаем проекции точки K, которая

делит проекции прямой в заданном отношении.

б) в)

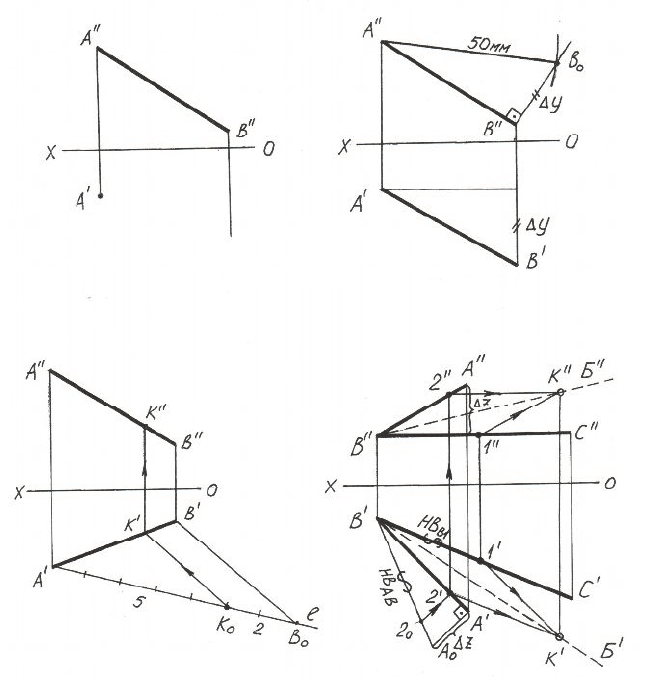
Рисунок 6.1 – Примеры решения обратных метрических задач:

а – построение прямой заданной длины;

б – деление прямой в заданном отношении;

в – деление угла на равные части

а)

Пример 3. Дан угол АВС. Необходимо разделить угол пополам

(провести биссектрису угла). Решение задачи представлено на ри-

сунке 6.1,в.

Биссектрису угла можно провести, если на сторонах угла отло-

жить равные отрезки и с помощью точек 1 и 2 построить параллело-

грамм В2K1, а далее найти проекции точки K, определяющей биссек-

трису. Сторона угла ВС в задаче является горизонталью, поэтому го-

ризонтальная проекция есть НВ.

На стороне угла ВС возьмём произвольный отрезок В1. Опреде-

лим натуральную величину стороны АВ методом прямоугольного

треугольника. На гипотенузе прямоугольного треугольника отложим

натуральную величину отрезка В1. Полученную точку 2

возвращаем

на проекции. С помощью точек 1 и 2 строим искомый параллело-

грамм и через проекции точки K проводим проекции биссектрисы.

Пример 4. Построить прямой угол АВС, если известны одна про-

екция стороны ВС и плоскость угла, заданная следами.

Задачу решим методом совмещения (вращением плоскости угла

вокруг горизонтального следа до совмещения с плоскостью Н). Ре-

шение задачи приведено на рисунке 6.2.

Сначала с помощью горизонталей построим горизонтальную

проекцию прямой ВС. Далее вторым способом построим совмещен-

ный фронтальный след заданной плоскости. Затем обычным для ме-

тода совмещения способом определим натуральную величину пря-

мой ВС – В

На натуральной величине прямой ВС построим прямой угол АВС.

Точку А

вернём на проекции и получим проекции искомого прямого

угла.

Пример 5. На прямой АВ найти точку K, отстоящую от точки В на

30 мм. Через точку K и точку С провести горизонталь длиной 50 мм

(рисунок 6.3,а).

Сначала методом прямоугольного треугольника определим нату-

ральную величину прямой АВ, на которой откладываем 30 мм и по-

лучаем точку K

Далее получаем проекции точки K и через них проводим проек-

ции горизонтали. Длину горизонтали 50 мм откладываем на горизон-

тальной проекции горизонтали.

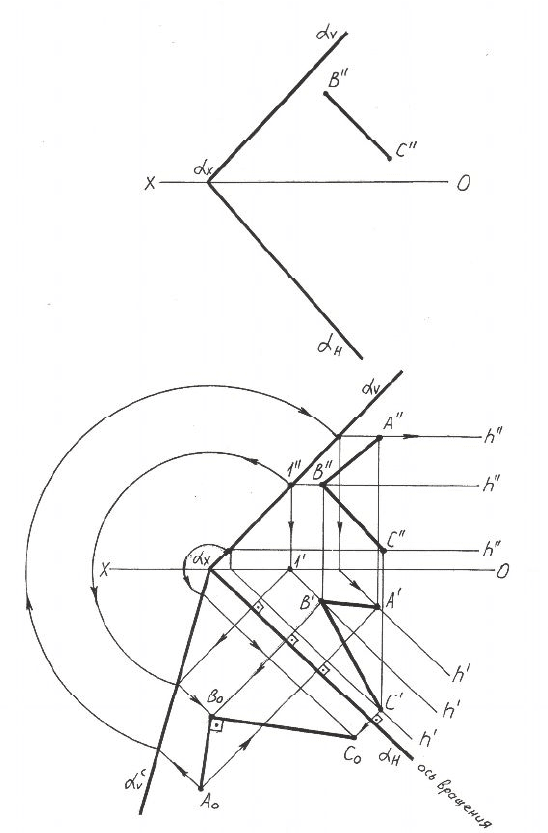
Рисунок 6.2 – Построение угла заданной величины по стороне угла

и его заданной плоскости

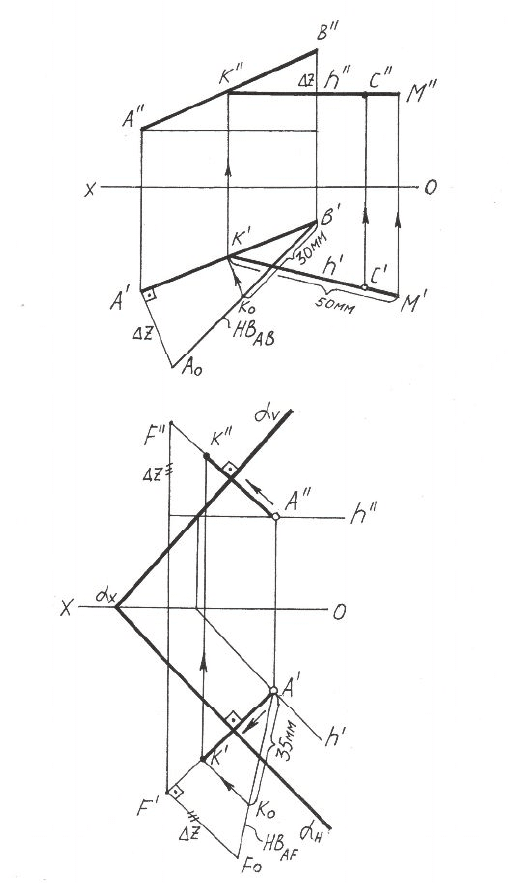
Рисунок 6.3 – Примеры решения обратных метрических задач

а)

б)

Пример 6. Из любой точки заданной плоскости восстановить пер-

пендикуляр длиной 35 мм (рисунок 6.3,б).

Сначала с помощью горизонтали, проведённой в плоскости, ука-

жем произвольную точку А. Далее из точки А восстановим проекции

перпендикуляра, которые проводим перпендикулярно следам плос-

кости.

Так как 35 мм нельзя отложить на проекциях перпендикуляра, ог-

раничим перпендикуляр в произвольной точке F и определим нату-

ральную величину отрезка АF методом прямоугольного треугольника.

На натуральной величине перпендикуляра отложим 35 мм и полу-

чим точку K

. Точку K

возвратим на проекции и получим искомые

проекции перпендикуляра длиной 35 мм.

Список литературы

1. Гордон, В. О. Курс начертательной геометрии / В. О. Гордон,

М. А. Семенцов-Огиевский. – М. : Высш. шк., 2002. – 247 с.

2. Кирин, Е. М. Теоретические основы решения задач по начерта-

тельной геометрии / Е. М. Кирин, М. Н. Краснов. – Пенза : Изд-во

Пенз. гос. ун-та, 2007. – 147 с.

Учебное издание

Кирин Евгений Михайлович

Метрические задачи

в курсе начертательной геометрии

Редактор О. Ю. Ещина

Компьютерная верстка М. Б. Жучковой

Подписано в печать 17.09.10.

Формат 60´84

. Усл. печ. л. 3,95.

Тираж 75. Заказ № 553.

Издательство ПГУ.

440026, Пенза, Красная, 40.