Кирин Е.М. Метрические задачи в курсе начертательной геометрии
Подождите немного. Документ загружается.

10
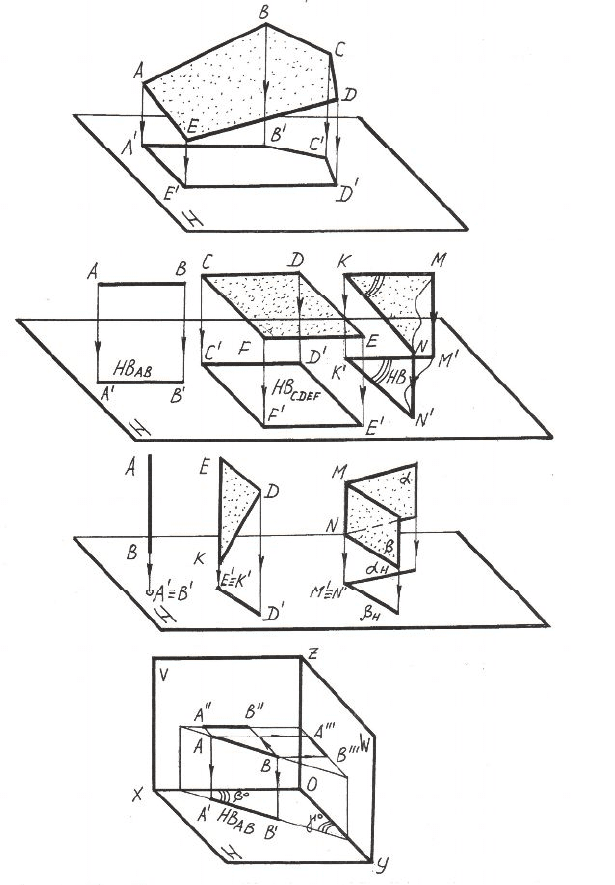
Рисунок 1.2 – Метрические свойства ортогонального проецирования
а)
б)
в)
г)
11
- плоская фигура или плоский угол, параллельные плоскости
проекций, проецируются на эту плоскость в натуральную величину
(см. рисунок 2.1,б);
- если плоская фигура и плоский угол перпендикулярны плоско-
сти проекций, то они проецируются на эту плоскость в виде прямой
линии («вырождаются» в линию) (см. рисунок 2.1,в);
- расстояние между геометрическими объектами изображается
на проекциях в натуральную величину, если это расстояние парал-
лельно плоскости проекций;
- расстояние от точки до прямой изображается на проекциях в
натуральную величину, если прямая является проецирующей прямой
и «вырождается» на одной из проекций в точку. На рисунке 2.2,а
показано расстояние между точкой и фронтально-проецирующей
прямой;
- расстояние между параллельными прямыми изображается в
натуральную величину, если они являются проецирующими и «вы-
рождаются» на одной из проекций в точки (см. рисунок 2.2,б);
- расстояние от точки до плоскости изображается в натуральную
величину, если плоскость является проецирующей и на одной из
проекций «вырождается» в линию (см. рисунок 2.2,в);
- расстояние между двумя параллельными плоскостями изобра-
жается в натуральную величину, если плоскости являются одно-
имённо-проецирующими и «вырождаются» на одной из проекций в
линии (рисунок 2.2,г);
- угол между прямой и плоскостью изображается в натуральную
величину, если плоскость является проецирующей, а прямая – лини-
ей уровня. В задаче на рисунке 2.2,д определён угол между фронта-
лью и фронтально-проецирующей плоскостью;
- угол между двумя плоскостями изображается в натуральную
величину, если обе плоскости являются одноимённо-проецирую-
щими (или если их общее ребро является проецирующим) (см. рису-
нок 2.2,е);
- плоско-параллельный перенос геометрического объекта или
плоскости проекций не изменяет вида и размеров проекции объекта.
12
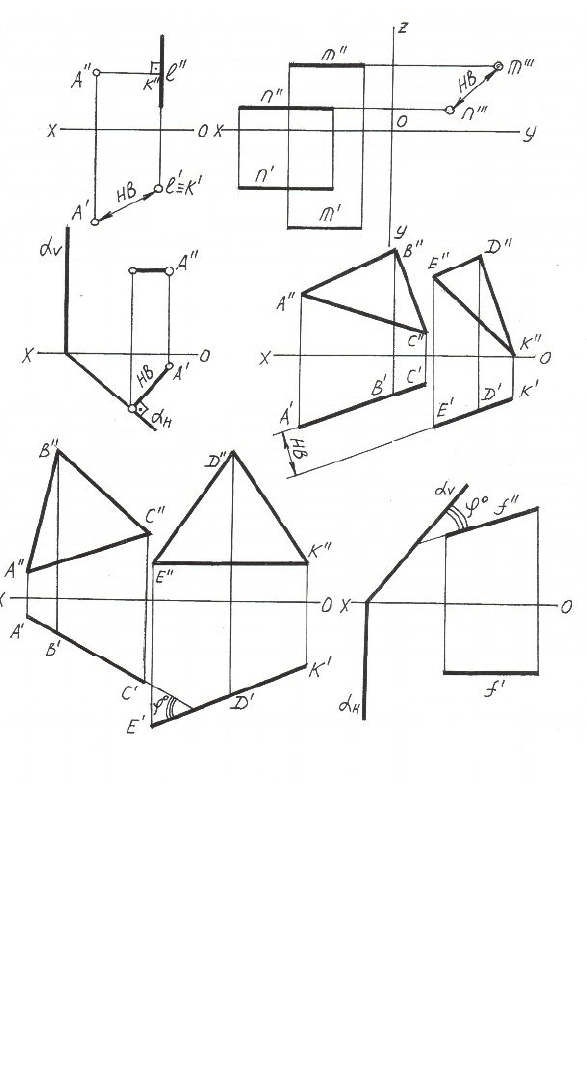
Рисунок 2.2 – Частные случаи определения расстояний
и углов между геометрическими объектами
а
)
б
)
в
)
г
)
е
)
а
)
д
)

13
2.2 Теорема прямого угла
Теорема прямого угла является одной из основных теорем, опре-
деляющих многие построения в метрических задачах. Теорема за-
ключается в следующем.
Пусть в пространстве имеется прямой угол АВС. Один катет АВ
параллелен какой-либо плоскости Q, другой катет не параллелен и не
перпендикулярен упомянутой плоскости (рисунок 2.3).
В пространстве угол АВС прямой. Докажем, что угол А
/
В
/
С
/
тоже
прямой. Фигура АВВ
/
А
/
– прямоугольник, следовательно, отрезок АВ
перпендикулярен проецирующей плоскости ВСС
/
В
/
, так как он пер-
пендикулярен двум пересекающимся прямым ВС и ВВ
/
по условию и
построению. Но АВ параллельна А
/
В
/
, следовательно, А
/
В
/
перпенди-
кулярна плоскости ВСС
/
В
/
, поэтому А
/
В
/
перпендикулярна В
/
С
/
, т.е.
угол А
/
В
/
С
/
равняется 90°.
Таким образом, если один катет прямого угла параллелен какой-
либо плоскости (или плоскости проекций), а другой катет не парал-
лелен и не перпендикулярен упомянутой плоскости, то прямой угол
проецируется на эту плоскость в натуральную величину, т.е. в 90°.
Теорема прямого угла распространяется не только на пересекаю-
щиеся перпендикулярные прямые (рисунок 2.4,а), но и на перпенди-
кулярные скрещивающиеся прямые (рисунок 2.4,б).
2.3 Перпендикуляр к плоскости
Из курса элементарной геометрии известно, что прямая перпен-
дикулярна плоскости, если она перпендикулярна двум любым пере-
секающимся прямым, находящимся в этой плоскости. Проведение
перпендикуляра к плоскости (опускание перпендикуляра) и восста-
новление перпендикуляра из плоскости называется прямой задачей
.
Проведение плоскости перпендикулярно заданной прямой называет-
ся обратной задачей. В обоих случаях прямой задачи для того, чтобы
опустить перпендикуляр на плоскость или восстановить (восставить)
его из плоскости, необходимо в плоскости провести две пересекаю-
щиеся прямые, с помощью которых можно провести перпендикуляр
к плоскости. При решении обратной задачи плоскость задают двумя
пересекающимися прямыми или следами.
14
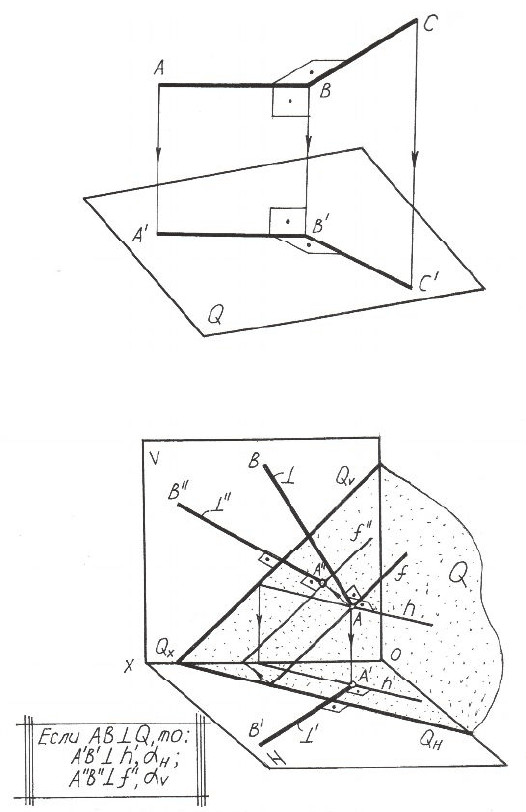
Рисунок 2.3 – Теорема прямого угла
Рисунок 2.5 – Вывод алгоритма проведения
перпендикуляра к плоскости
15
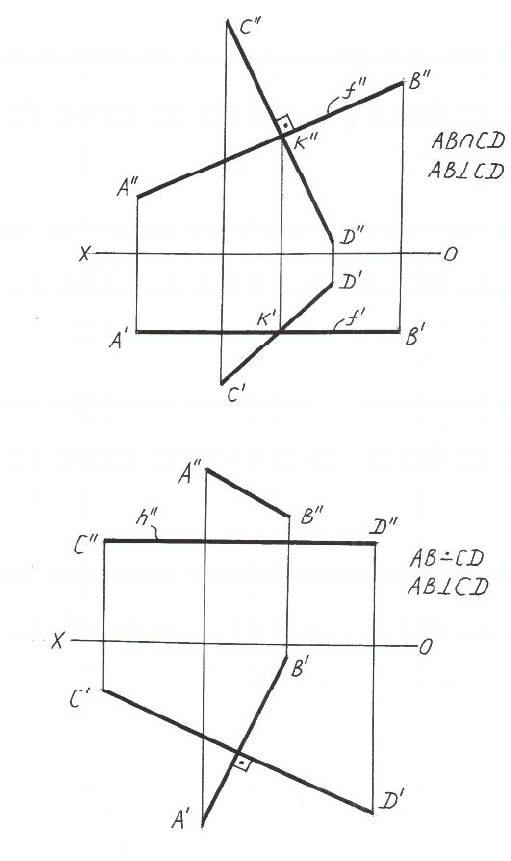
Рисунок 2.4 – Использование теоремы прямого угла
для пересекающихся и скрещивающихся прямых
а
)
б
)
16
Так как в начертательной геометрии рассматриваются не сами
геометрические объекты, а их проекции, то необходимо рассмотреть
вопрос о том, как проводить проекции перпендикуляра к плоскости.
Для разработки алгоритма проведения проекций перпендикуляра к
плоскости рассмотрим пространственный макет двух плоскостей
проекций, в системе которых расположена плоскость общего поло-
жения Q (рисунок 2.5).
Возьмём в плоскости Q любую точку А и восстановим из неё пер-
пендикуляр. Для этого в плоскости надо предварительно провести
две пересекающиеся прямые. Наиболее целесообразно в качестве
этих прямых взять горизонталь h и фронталь f.
Далее из точки А восстановим перпендикуляр так, чтобы он был
перпендикулярен горизонтали и фронтали. Спроецируем точку А на
плоскости проекций H и V. Из проекций точки А проведём горизон-
тальную и фронтальную проекции перпендикуляра.
В соответствии с теоремой прямого угла и исходя из пространст-
венного макета проекции перпендикуляра должны быть проведены
следующим образом:
- горизонтальная проекция перпендикуляра проводится перпен-
дикулярно горизонтальной проекции горизонтали или горизонталь-
ному следу плоскости;
- фронтальная проекция перпендикуляра проводится перпенди-
кулярно фронтальной проекции фронтали или фронтальному следу
плоскости.
Правило проведения перпендикуляра к плоскости в алгоритмиче-
ской форме записано на рисунке 2.5. Если использовать алгоритм в
направлении «слева-направо», то он позволяет решать прямую зада-
чу, т.е. опускать перпендикуляр на плоскость или восстанавливать
его из плоскости. Если использовать алгоритм в направлении «спра-
ва-налево», то он позволяет проводить плоскость, перпендикулярную
заданной прямой. На рисунке 2.6 представлены примеры решения
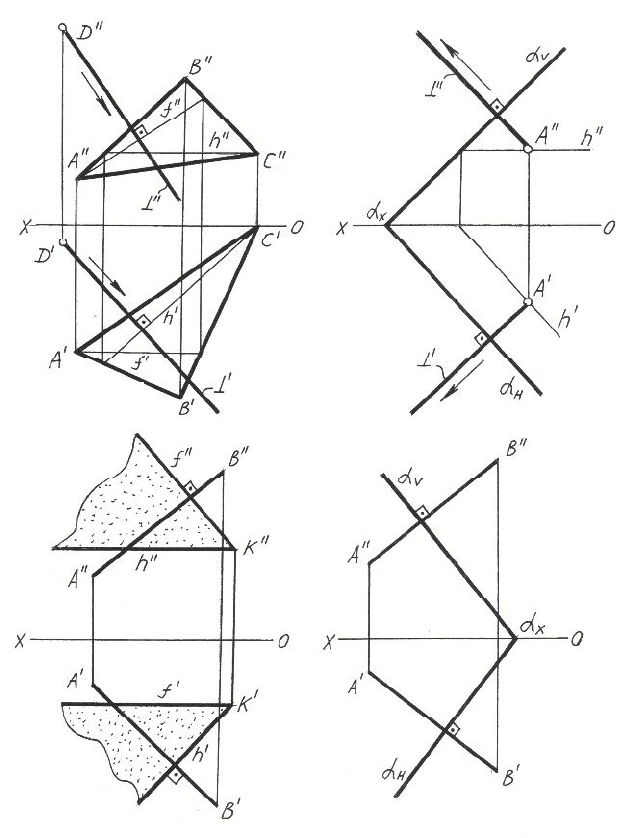
прямой и обратной задач. На рисунке 2.6,а из точки D опущен пер-
пендикуляр на плоскость треугольника АВС. На рисунке 2.6,б из
произвольной точки А, принадлежащей плоскости, заданной следа-
ми, восстановлен перпендикуляр, проекции которого проведены
перпендикулярно следам заданной плоскости.
17
Рисунок 2.6 – Примеры решения прямой и обратной задач
о перпендикуляре к плоскости
а)
б)
в)
г)
18
На рисунке 2.6,в, г показано, как надо проводить плоскость, про-
ходящую через точку K перпендикулярно заданной прямой АВ.
В первом случае плоскость задана двумя пересекающимися прямы-
ми – горизонталью и фронталью, а в другом случае – следами.
2.4 Перпендикулярность двух прямых
Перпендикулярность двух прямых частично рассмотрена в теоре-
ме прямого угла. Однако теорема прямого угла может быть исполь-
зована лишь в том случае, когда один из катетов прямого угла парал-
лелен какой-либо плоскости проекций.
Задача осложняется, если катеты прямого угла являются прямыми
общего положения. В этом случае ни на одной проекции угол не изо-
бражается в натуральную величину.
Для решения задачи целесообразно использовать методы преобра-
зования с целью перевода одной из сторон прямого угла из общего
положения в частное.
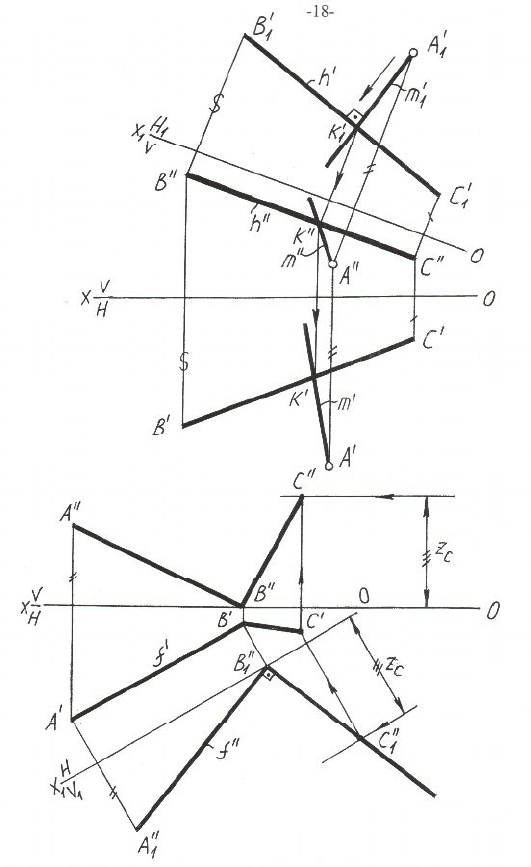
На рисунке 2.7,а представлено построение прямой m, проведён-
ной через точку А перпендикулярно прямой ВС и пересекающей её в
точке K. Задача решена методом перемены плоскостей проекций (за-
меной Н на Н
1
). В новой системе плоскостей проекций прямая ВС
становится горизонталью, в связи с чем из новой горизонтальной
проекции точки на основании теоремы прямого угла можно опустить
перпендикуляр на прямую ВС.
На рисунке 2.7,б представлено решение задачи о построении пря-
мого угла АВС, если заданы проекции стороны АВ.
Заменой плоскости V на V
1
переводим прямую общего положения
АВ в положение фронтали. Далее на основании теоремы прямого уг-
ла из точки В
1
//
под углом 90° проводим направление другой стороны
прямого угла, на которой берём произвольную точку С
1
//
, затем –
произвольную точку С
/
. Точку С
//
находим с помощью аппликаты
точки С.
Далее будет рассмотрен другой способ построения двух перпен-
дикулярных прямых общего положения.
19
Рисунок 2.7 – Построение прямого угла между прямыми общего положения
методом перемены плоскостей проекций
а)
б)
