Кириченко М.Ф., Матвієнко В.Т. Аналіз та синтез керованих систем
Подождите немного. Документ загружается.


41
p p P S b A c( ) ( ) ( ) ( , ( )) ,2 1 1 1
2 2
= −
T
де
A A b c
( ) ( ) .1 0
1 1
= +
T
На кроку m розглядається наступна система рівнянь
d t
dt
m t t
m m
x
A x b u
( )
( ) ( ) ( ) ,= − +1
де
A A b u( ) ( ) ( ) ,m m t
m m
−
=
−
+
− −
1 2
1 1
для
замкнутої
системи
,
якій
необхідно
забезпечити
наступні
коефіцієнти
характеристичного
рівняння
p a p P S b A c( ) ( ) ( ) ( , ( )) ,m m m m
T
m m
= = − − − −1 1 1
обираючи
відповідним
чином
вектор
c
m
[ 2 ] .
Таким
чином
,
завдання
побудови
модального
регулятора
зводиться
до
наступної
задачі
керування
системою
з
дискретним
аргументом
p p P S b A c
A A b c
( ) ( ) ( ) ( , ( )) ,
( ) ( ) , , , , ,
k k k k
k k k m
T
k k
k k
T
+ = −
+ = + = −
+ +
+ +
1
1 012 1
1 1
1 1
Κ
з
початкового
стану
p
p
A
A
(
)
,
(
)
0
0
=
=
у
фінальний
p a( )m
a
a
a
n
= =
1
2
Μ
.
Тут
вектор
p
T
n
p p p= ( , , )
,1 2
Κ
визначається
умовою
det( ) ,
λ λ λ
E A
n
n n
n
p p− = + + +
−
1
1
Κ
P( )
( )
( ) ( )
( ) ( ) ( )
,k
p k
p k p k
p k p k p k
n n n
=
− − −
1 0 0 0
1 0 0
1 0
1
1
2 1
1 2 3
Κ
Κ
Κ
Λ Λ Λ Λ Λ
Κ
S b A b A b( , ( )) ( , , ( ) ) .
k k
n
k
k k
+ +
−
+
=
1 1
1
1
Κ
Розглянемо
керування
для
системи
(7.1)
з
зовнішнім
збуренням
на
керування
u
Cx
u
(
)
(
)
t
t
=
−
, (7.4)
де
u
−
m -
вимірний
вектор
постійних
впливів
.
В
результаті
функціонування
системи
керування
(7.1),
вектор
стану
x
(t)
при
t
→
∞
буде
прямувати
до
деякої
точки
у
фазовому
просторі
~
x
.
Визначимо
цю
точку
з
умови
,
коли
t
→
∞

42
A
x
B
C
x
u
~
(
~
)
+
−
=
0
.
Тоді
(
)
~
A
BC
x
B
u
+
=
і шукана точка у фазовому просторі має вигляд
~
( )x A BC Bu= +
−1
, (7.5)
до
якої
прямує
траєкторія
системи
(7.1)
при
t
→
∞
.
Зворотна
матриця
до
матриці
A+BC існує
відповідно
до
необхідної
умови
асимптотичної
стійкості
замкнутої
системи
(7.1),
тому
що
коефіцієнт
характеристичного
рівняння
замкнутої
системи
a
n
n
= − + >
−
( ) det( )1 0
1
A BC
.
При
проектуванні
асимптотично
стійких
систем
керування
задається
точка
x
у
фазовому
просторі
,
в
яку
повинна
перейти
динамічна
система
з
постійним
впливом
на
керування
(7.4).
Обираючи
зовнішні
впливи
для
асимптотичної
стійкої
системи
(7.1)
з
множини
[ ]
( )
[
]
( )
u u A BC B x E A BC B A BC B v v R
1
∈ + + − + +
∀ ∈
−
+
−
+
−
: ( ) ,
m
m
1 1
,(7.6)
ми
прагнемо
забезпечити
збіжність
траєкторії
системи
до
точки
x
у
фазовому
просторі
.
У
випадку
,
коли
( )
[
]
x A BC B x 0
T
Z
T
+
=
−1
,
то
система
(7.5)
має
точний
розв
'
язок
і
система
керування
(7.1)
досягає
точки
фазового
простору
x
,
де
( )
[
]
( )
[
]
( )
[
]
Z
T
n
A BC B E A BC B A BC B+
= − + +
− − −
+
1 1 1
.
Якщо
( )
[
]
x A BC B x 0
T
Z
T
+
>
−1
,
тоді
система
керування
(7.1)
не
досягає
точки
фазового
простору
x
.
У
цьому
випадку
вектор
зовнішніх
збурень
на
керування
визначається
з
співвідношенням
( )
min
u
A BC Bu x+ −
−1
2
. (7.7)
З
умови
(7.7)
знаходимо
,
що
при
( ) ( ) ( )
( )
[ ]
u B A BC A BC B B A BC x
A BC B x
T T
= + +
+ =
= +
− −
+
−
−
+
1 1 1
1
T T
(7.8)
досягається
мінімум
функціоналу
(7.7).
У
цьому
випадку
система
керування
досягає
точки
у
фазовому
просторі

43
( ) ( ) ( )
[
]
( )
( ) ( )
[ ]
∃
,
x A BC B B A BC A BC B B A BC x
A BC B A BC B x
= + + + + =
= + +
− − −
+
−
− −
+
1 1 1 1
1 1
T T
T T
(7.9)
а квадрат похибки досягнення системою керування (7.1) точки
x
має вигляд
(
)
(
)
( ) ( )
[ ]
( )
[ ]
( )
[ ]
{ }
ε
2
1 1
1 1
( , )
∃ ∃
.
x B x x x x
x x x A BC B A BC B x
x x A BC B xx A BC B
= − − =
= − + + =
= − + +
− −
+
−
+
−
T
T T
T T
tr
(7.10)
Величину
квадрата
помилки
досягнення
(7.10)
системи
можна
зменшити
за
рахунок
зміни
матриці
B, тобто
за
рахунок
вибору
прикладення
керуючих
впливів
(
синтезу
структури
керування
).
Змінимо
матрицю
B
оптимальним
чином
.
Для
цього
скористаємося
градієнтною
процедурою
визначення
матриці
B
на
k+1
-
му
кроці
B B x B
Bk k k
grad
k
+
= −
1
2
ρ ε
( , ) . (7.11)
Для знаходження grad
k
B
x B
ε
2
( , ) скористаємося наступною теоремою.
Теорема. Якщо матриця A+BC має повний ранг, то
( )
[
]
{
}
( ) ( )
[ ]
( )
[ ]
( )
{
( )
[ ]
( )
[ ]
( )
}
grad
T
B
D A BC B F
C A BC B A BC B FD A BC B A BC
A BC B FD A BC B A BC
tr
.
+ =
= + + + + −
− + + +
−
+
− −
+
−
+
−
−
+
−
+
−
1
1 1 1 1
1 1 1
Доведення. Неважко показати, що для матриці Х, що має повний ранг,
виконується співвідношення
∂
∂
∂
∂
b b
ij ij
X X X X
+ + +
= −
. (7.12)
Тоді
( )
[
]
( )
[
]
∂
∂
∂
∂
b b
ij ij
D A BC B F D A BC B F+ = +
=
−
+
−
+
1 1
( )
[ ]
( )
[ ]
( )
[ ]
= − + +
+
−
+
− −
+
D A BC B A BC B A BC B F
1 1 1
∂
∂
b
ij
,
де b
ij
- елемент матриці В.
Легко отримати і наступне співвідношення
( )
[
]
( )
( )
∂
∂
b
ij
i j i
A BC B y c A BC B y
T
+ = − + +
− −1 1
0 0 0 0, , , , , ,Κ Κ .
Вектор
-
стовпчик
y
i
в
останній
матриці
розташований
на
j -
му
місці
.
Тут
прийняті
наступні
позначення

44
( ) ( )
A BC y y y C
c
c
c
+ = =
−1
1 2
1
2
, , , ,Κ
Μ
n
T
T
m
T
.
Тоді
( )
[
]
{
}
∂
∂
b
ij
tr D A BC B F+ =
−
+
1
( )
[ ]
tr
∂
∂
b
ij
D A BC B F+
=
−
+
1
( )
[
]
( ) ( )
[
]
{
= + + + −
−
+
− −
+
tr D A BC B y c A BC B A BC B F
1 1 1
i j
T
( )
[
]
( )
( )
[
]
}
− + +
−
+
−
+
D A BC B y A BC B F
1 1
0 0 0 0, , , , , ,Κ Κ
i
.
Увівши
позначення
( )
[ ]
K A BC B
k
k
k
= + =
−
+
1
1
2
T
T
n
T
Μ
,
одержимо
( )
[
]
{
}
( )
∂
∂
b
ij
i
T T T T T
j
T
tr D A BC B F y K D F B A BC c+ = + −
−
+
−1 1
− = − −y K D F k y Gc y G k
i
T T T T
j i
T
j i
T
j1
,
де
( )
G K D F K B A BC G K D F= + =
−
T T T T T T T T
T
1
1
, .
Тоді
( )
[
]
∂
∂
B
D A BC B Ftr +
=
−
+
1
y Gc y Gc y Gc
y Gc y Gc y Gc
y Gc y Gc y Gc
y G k y G k y G k
y G k y G k y G k
y G k y G k y G k
1 1 1 2 1
2 1 2 2 2
1 2
1 1 1 1 1 2 1 1
2 1 1 2 1 2 2 1
1 1 1 2 1
T T T
n
T T T
n
n
T
n
T
n
T
n
T T T
n
T T T
n
n
T
n
T
n
T
n
Κ
Κ
Κ Κ Κ Κ
Κ
Κ
Κ
Κ Κ Κ Κ
Κ
−
=
( ) ( )
=
−
=
y
y
y
G c c c
y
y
y
G k k k
1
2
1 2
1
2
1 1 2
T
T
n
T
n
T
T
n
T
n
Μ
Κ
Μ
Κ, , , , , ,
( ) ( )
= + − + =
− −
A BC GC A BC G K
1 1
1
T T
T
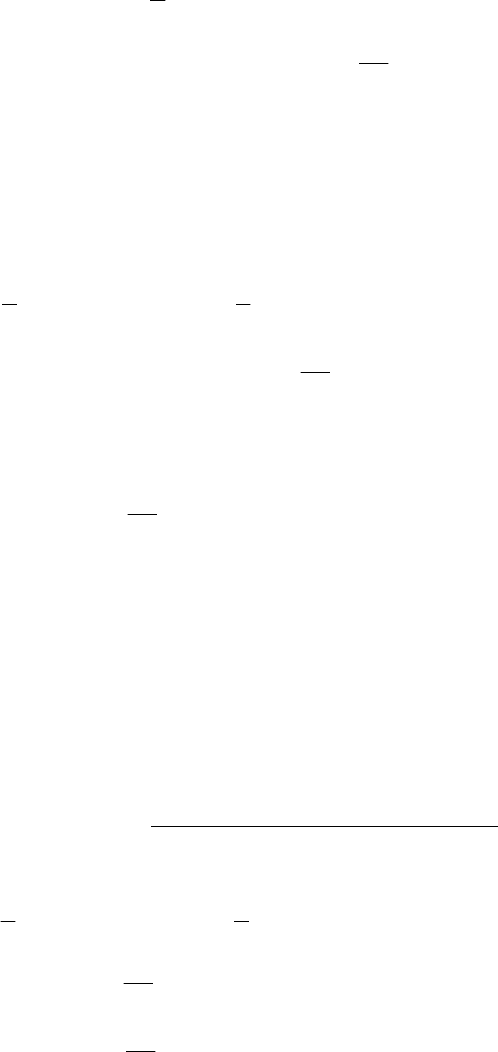
45
( ) ( )
[
]
( )
[
]
( )
{
= + + + + −
− −
+
−
+
−
C A BC B A BC B FD A BC B A BC
1 1 1 1
( )
[ ]
( )
[ ]
( )
− + + +
−
+
−
+
−
A BC B FD A BC B A BC
1 1 1
T
.
Тим самим теорема доведена.
Використовуючи цей результат одержимо в явному виді наступний
вираз
(
)
( )
[ ]
( )
[ ]
( )
[ ]
( )
[ ]
( )
grad
k
k k m k k
T
n k k k k k
T
B
x B
C A B C B E A B C B xx
E A B C B A B C B A B C
ε
2
1 1
1 1 1
,
.
=
= + − + ×
× − + + +
− −
+
−
+
−
+
−
Приведемо необхідні умови оптимального вибору матриці В для
функціоналу (7.10).
Запишемо приріст функціоналу (7.10) по вектор стовпчикам матриці В
(
)
(
)
ε ε ε
2 2
x B b e x B, ,+ − =
i i i
T
∆
( ) ( )
[
]
− + + +
×
−
+
+
tr
i i i
T
i i i
T T
A BC b c B b e xx
ε ε
∆ ∆
1
(7.13)
(
)
(
)
[
]
}
× + + +
−
A BC b c B b e
ε ε
i i i
T
i i i
T
∆ ∆
1
+
( )
[
]
( )
[
]
+ + +
−
+
−
tr
T
A BC B xx A BC B
1 1
,
i
m
=
1
2
,
,
,
Κ
,
де
c
i
T
- вектор рядок матриці С, e
i
- i-й орт одиничної матриці,
∆
b
i
- приріст
для b
i
вектор стовпця матриці В ,
ε
i
≥
0.
Припускаємо
,
що
матриця
A+BC
має
повний
ранг
.
Використовуючи
результат
робіт
[7]
обернену
матрицю
у
виразі
(7.13)
можна
записати
в
наступному
виді
( )
( )
(
)
(
)
( )
A BC b c A BC
A BC b c A BC
c A BC b
+ + = + −
+ +
+ +
−
− −
−
ε
ε
ε
i i i
T
i i i
T
i i
T
i
∆
∆
∆
1
1 1
1
1
.
Тоді
формула
(7.13)
набуде
вигляду
(
)
(
)
ε ε ε
2 2
x B b e x B, ,+ − =
i i i
T
∆
( )
[
]
( )
[
]
{
}
= + + −
−
+
−
tr
T
A BC B xx A BC B
1 1
(7.14)
( )
[
]
( )
[
]
{
}
− + + + +
−
+
−
tr
i i
T T
i i
T
A BC B f g xx A BC B f g
1 1
,
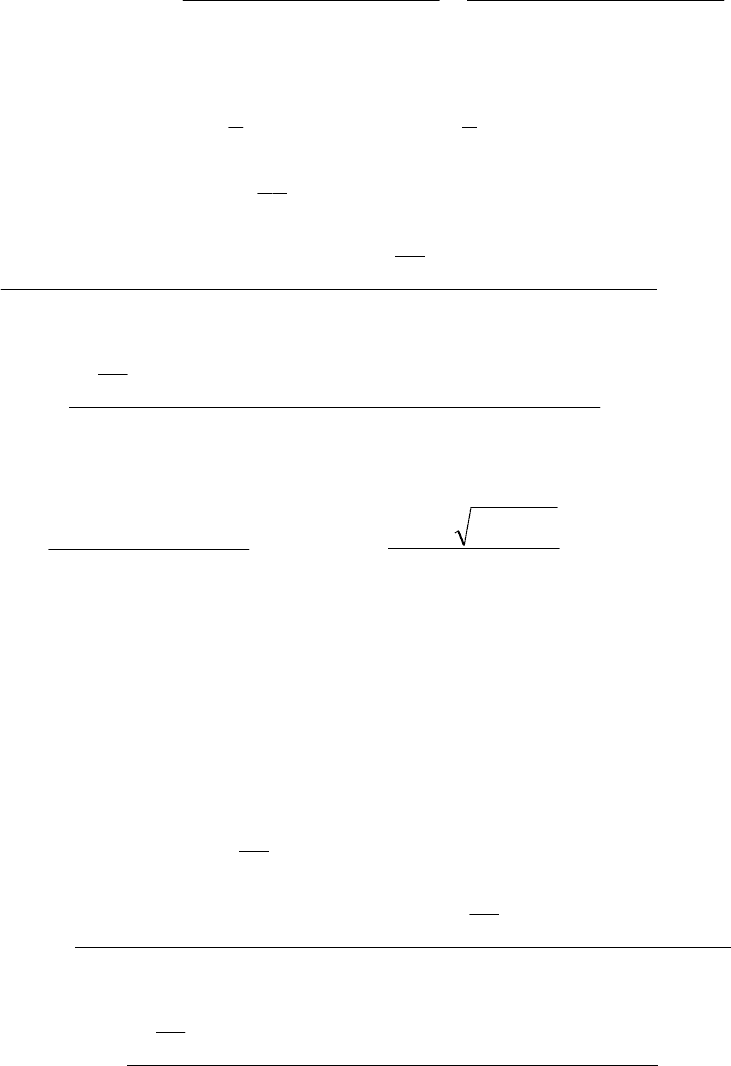
де
вектори
(
)
f A BC b
i i i
= +
−
ε
1
∆ ,
46
(
)
( )
(
)
( )
g e
c A BC B
c A BC b
c A BC b e
c A BC b
i
T
i
T
i
T
i i
T
i
i
T
i i i
T
i i
T
i
= −
+
− +
−
+
− +
−
−
−
−
1
1
1
1
1 1
ε
ε
ε
∆
∆
∆
.
Псевдообернену матрицю у виразі (7.14) розпишемо використовуючи
математичний апарат збурення матриць [ 8 ].
(
)
(
)
ε ε ε
2 2
x B b e x B, ,+ − =
i i i
T
∆
( )
[
]
= − + +
−
+
f xx A BC B g
i
T T
i
T
1
( )
[
]
( ) ( )
[
]
( )
[ ]
+
+ + +
+ +
+
−
+
− −
+
−
+
f A BC B B A BC xx A BC B g
g A BC B f
i
T T T
i
i
T
i
T
T
T
1 1 1
1
1
(7.15)
( )
[
]
( )
[
]
( )
[ ]
+
+ +
+ +
−
+
−
+
−
+
f xx A BC B g f A BC B g
g A BC B f
i
T T
i i
T
i
i
T
i
T T
1 1
1
1
.
Умови на вибір
ε
i
випливають з рівняння (7.15)
( )
ε
i
i
T
i
≠ −
+
−
1
1
c A BC b∆
,
ε
i
y y x
x
≠
− ± +
2
4
2
, (7.16)
де
( )
(
)
( )
[
]
( )
x
i
T
i i
T
i
T
i
= + − + +
− −
+
−
c A BC b e c A BC A BC B b
1 1 1
∆ ∆ ,
( )
[
]
( ) ( ) ( )
y
i
T
i
T
i
T
i
= + + − + − +
−
+
− − −
e A BC B A BC B c A BC B c A BC b
1 1 1 1
∆ .
Якщо матриця В доставляє мінімум функціоналу (10) і матриця A+BC
має повний ранг, то відповідно до [6, 7, 8]
( )
[
]
− + +
−
+
f xx A BC B g
i
T T
i
T
1
( )
[
]
( ) ( )
[
]
( )
[ ]
+
+ + +
+ +
+
−
+
− −
+
−
+
f A BC B B A BC xx A BC B g
g A BC B f
i
T T T
i
i
T
i
T
T
T
1 1 1
1
1
( )
[
]
( )
[
]
( )
[ ]
+
+ +
+ +
≥
−
+
−
+
−
+
f xx A BC B g f A BC B g
g A BC B f
i
T T
i i
T
i
i
T
i
T T
1 1
1
1
0
для будь-яких
ε
i
≥
0 ,
i
m
=
1
2
,
,
,
Κ
і
при
цьому
виконуються
умови
(7.16).
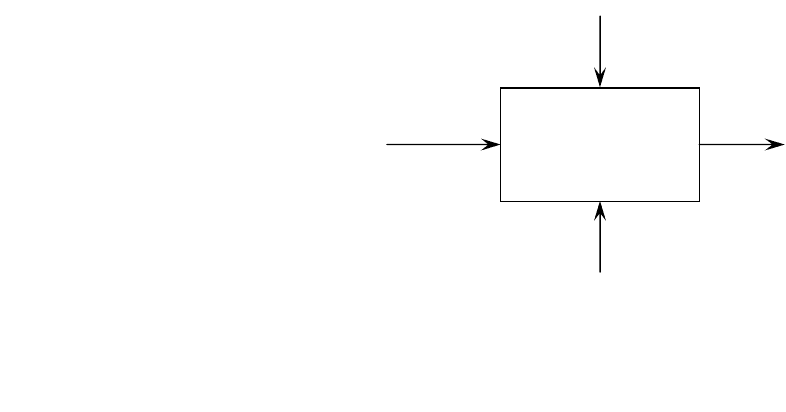
Для
чисельних
процедур
градієнтного
спуску
по
оптимальному
вибору
матриці
В
можна
скористатися
формулою
(7.15).
47
8. Побудова множинних фільтрів для лінійних алгебраїчних
систем
В технічних задачах регулювання, при використанні теорії
оптимального керування виникає необхідність у процедурах оцінювання і
фільтрації. Оцінка стана системи керування або невідомих параметрів об'єкта
є однією з важливих проблем у задачах керування і реставрації сигналу в
цифровій обробці інформації. В даному параграфі побудований клас лінійних
фільтрів [3] для оцінки параметрів об'єкта, що описується системою
алгебраїчних рівнянь.
Загальна блок-схема системи з зображенням впливів на неї, її
параметри і вимірювані дані про стан системи, зображені на малюнку.
Для даного малюнка введені наступні позначення:
u - керуючий вплив, що вибирається, значення якого відомі;
f - збурення, значення їх невідома, відомо апріорна множина
f
Ω
можливих значень збурень;
p - параметр, у який може входити вектор стану системи, значення
невідомі;
y - вимірювані дані про стан системи, значення відомі.
Зазначені дії на систему, параметри, вимірювані дані можуть бути
скалярами, векторами, матрицями, функціями.
Рівняння математичної моделі системи керування у вищеописаних
термінах має загальний вигляд
u
p
y
f

48
)
,
,
(
f
u
p
A
y
=
, (8.1)
де А - відома функція.
При прийнятій моделі невідомих шумів для системи, що описується
рівнянням (1), можуть бути сформульовані наступні задачі:
Задача 1. Знайти при фіксованому u таку функцію
)
(
y
Ψ
, що
(
)
fp
Ω
,y,up
Ω
∈
∀
має
місце
умова
(
)
(
)
.0,u,pAΨp
=
(8.2)
У
загальному
випадку
при
фіксованому
u
існує
множина
( )
(
)
u
yΨ
Ω
таких
функцій
Ψ
(y)
,
яку
будемо
називати
множиною
фільтрів
.
Задача
2.
Знайти
при
фіксованому
u
оптимальну
функцію
(y)
Ψ
0
згідно
з
умовою
оптимальності
( )
( )
( )
( )
( )
( )( )
−=
∈⋅∈
∈
f,u,pAΨpyΨ
fp
yΨ
ΩfΩp
uΩyΨ
,
0
maxminarg . (8.3)
Множини
(
)
fp
Ω,y,uΩ ,
( )
(
)
uΩ
yΨ
і функція (y)Ψ
0
будуються до
проведення експерименту.
Розглянемо модель системи, що представлена у загальному випадку
системою лінійних алгебраїчних рівнянь
(
)
(
)
yfudpuA
=
+
+
, (8.4)
де матриця
(
)
nm
R
×
∈uA , вектори
(
)
m
R∈ud ,
m
R
∈
f
,
m
R∈y .
Матриця A і вектор d відомі параметри, досліджуваного об'єкта.
У випадку, коли відомо апріорна множина
f
Ω
значень шумів f і
маючи систему рівнянь, якій задовольняє вимірюваний вектор y, можна
оцінити апостеріорну множину
Ω
f
y|
значень f і з використанням останньої
і апріорної множини ),,(
fp
yu
Ω
Ω
значень параметрів p оцінити
апостеріорну повну множину fyyu
fp
,),,( ΩΩ
значень
параметрів
.
Апостеріорна
множина
значень
f (
множина
тих
значень
f ,
при
котрих
y
може
реалізуватися
при
деяких
значеннях
p
відповідно
до
системи
(8.4))
визначається
таким
чином

49
(
)
(
)
(
)
(
)
{
}
0udfyuAZfy
ff
=−−∩Ω=Ω
T
:|
, (8.5)
де
(
)
(
)
(
)
(
)
uAuAIuAZ
+
−=
m
T
,
I
m
- одинична матриця розмірності
m
m
×
,
(
)
A u
+
- псевдообернена матриця,
що визначається в такий спосіб [1]
( ) ( ) ( ) ( )
(
)
[
]
1
2
0
lim
−
→
+
+=
m
T
δ
δ IuAuAuAuA
T
.
Апостеріорна
повна
множина
оцінюваних
величин
p
(
множина
тих
значень
p
,
при
яких
реалізується
вимірюваний
вектор
y
і
шум
f
,
що
належить
множині
значень
(5))
визначається
таким
чином
=ΩΩ
fyyu
fp
,),,(
{
}
yfvvuAZudfyuApp
f
Ω∈∀∈+−−==
+ n
R,))(())()((: , (8.6)
де
(
)
(
)
(
)
(
)
uAuAIuAZ
+
−=
n
,
I
n
- одинична матриця розмірності n
×
n.
Множина (8.6) записана з умови знаходження розв'язку [7] системи (8.4)
відносно вектора p.
Для лінійної алгебраїчної системи, що описується рівнянням (8.1)
розглянемо задачу 1. Рівняння (8.2), отримане на підставі (8.4) при
0
f
=
буде мати вигляд
(
)
(
)
(
)
udpuAp
+
Ψ
=
, (8.7)
де функцію
(
)
Ψ ⋅
виберемо лінійною наступного виду
(
)
(
)
(
)
(
)
(
)
(
)
udyVpuAVudpuA
−
=
=
+
Ψ
, (8.8)
де
mn
R
×
∈V -
невідома матриця.
Якщо система (8.4) спостережна, тобто при з
0
f
=
системи
алгебраїчних рівнянь
(
)
(
)
udypuA
−
=
вектор
p
знаходиться однозначно, то з представлення (8.8)
(
)
puAVp
=
50
одержуємо умову
(
)
n
IuAV
=
, з якого матриця
V
mn
R
×
∈∀W
знаходиться
наступним способом
(
)
(
)
(
)
uAZWuAV
T
+=
+
mn
R
×
∈∀W
, (8.9)
де
+
A
псевдообрнена до матриці A,
(
)
(
)
(
)
(
)
uAuAIuAZ
+
−=
m
T
,
n
I - одинична матриця розмірності
n
n
×
.
Таким чином, у класі лінійних функцій множина фільтрів
(
)
⋅
Ψ
лінійної
алгебраїчної системи, що описується системою рівнянь (8.4), має вид
(
)
(
)
(
)
(
)
[
]
(
)
(
)
udyuAZWuAy −+=Ψ
+ T
mn
R
×
∈∀ W . (8.10)
У випадку присутності шуму f множина фільтрів (8.10) породить
множину конкуруючих оцінок
[
]
=−+=
+
d(u))(y))WZ(A(u)Ap
T
ˆ
[
]
++=
+
puA))WZ(A(u)A )(
T
(
)
(
)
(
)
[
]
mnT
R
×+
∈∀++ WfuAZWuA (8.11)
Якщо система (8.4) не спостережувана при f=0. Тоді для системи
(
)
(
)
udypuA
−
=
вектор p знаходиться неоднозначно
=−+−=
++
vuAuAIudyuAp
))()(())()((
n
n
R∈∀+−=
+
vvuAZudyuA
,))(())()(( . (8.12)
Тоді
у
випадку
присутності
шуму
f
,
без
обмеження
загальності
в
(8.12)
покладемо
p
v
=
,
множина
конкуруючих
оцінок
має
вигляд
[
]
=−+=
+
d(u))(y))WZ(A(u)Ap
T
ˆ
[
]
++=
+
puAu))WZ(A(u)A
)((
T
(
)
(
)
(
)
[
]
=+
+
fuAZWuA
T
[
]
++−+=
++
))(())()(()(()(
puAZudyuAuA)uWZ(A(u)A
T
(
)
(
)
(
)
[
]
=++
+
fuAZWuA
T
[
]
++=
++
puAuAuA)uWZ(A(u)A
)()()()(
T
[
]
puAZuAu))WZ(A(u)A
))(()((
T
++
+
(
)
(
)
(
)
[
]
fuAZWuA
T
++
+
.
