Кириченко М.Ф., Матвієнко В.Т. Аналіз та синтез керованих систем
Подождите немного. Документ загружается.


11
( )
=
+
−=
++
−=
++
2222
b
bb
AAIb
b
b
AAI
TT
n
T
T
n
k
kk
k
k
kk
22222
k
kk
k
kk
TTTTT
−+=
+−+=
+++
b
bb
AA
b
bb
AA
b
bb
AA
.
Наслідок 6. Якщо мають місце умови наслідку 4, то
)()()(
22
2
AIAIba,,AA,
R
k
kk
R
k
kk
T
n
T
n
−
−
−=∆
+
. (2.10)
За
умови
2
( bA)bb <Z
T
вирази ),(
1
ba,AA,
T
∆
й
),(
2
ba,AA,
T
∆
у
цьому
випадку
будуть
отримані
після
аналізу
випадку
лінійної
залежності
a
і
b
від
відповідно
вектор
-
стовпців
і
векторів
-
рядків
матриці
A
.
Випадок
3.
Вектори
a
і
b
лінійно
залежні
відповідно
від
вектор
-
стовпців
і
векторів
-
рядків
матриці
A
,
тобто
0)( =aAa
TT
Z , 0)( =bAb
TT
Z (2.11)
і
при
цьому
1
−=
+
aAb
T
. (2.12)
У
цьому
випадку
збурення
псевдооберненої
матриці
визначаються
відповідно
наступної
теореми
.
Теорема
3.
Якщо
для
матриці
nm
R
×
∈A ,
m
R
∈a ,
n
R
∈b
виконуються
умови
(2.11), (2.12),
то
мають
місце
співвідношення
1)( −=+ AabA rankrank
T
, (2.13)
−=−+=∆
+++
AabAba,AA, )(),(
T
+−
+
+
bAb
AbbA
aAa
AaaA
)(
)(
)(
)(
TT
T
TT
TT
R
R
R
R
aA)Ab
A)bbaAa
AabA
+
+
+
+ (
()(
R
RR
T
TTT
T
. (2.14)
Наслідок 7. Якщо виконані умови теореми 3, то
(
)
aAa
AaaA
ba,AA,
)(
),(
1
TT
T
T
R
++
+
=∆ . (2.15)
Справедливість твердження наслідку 7 перевіряється простою
підстановкою формули (2.15) у вираз для матриці )(
T
Z abA +
×
+−−
++
+
++
+
A)babAa
AabA
aAAb
A)bb
AbbA
aAa
AaaA
A
()(
)(
(
)(
)(
)(
RR
R
R
R
R
R
TTT
T
TT
T
TT
TT
TT
(
)
=+×
T
abA
+−−=
+
+
+
A)bb
AAbbA
aAa
AAaaA
AA
(
)(
)(
)(
R
R
R
R
T
TT
TT
TT
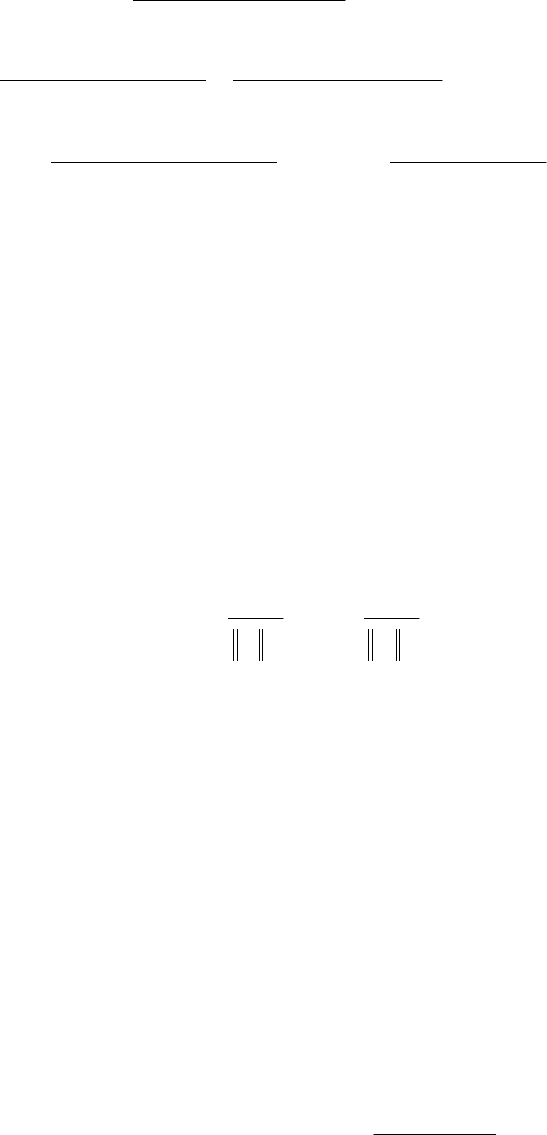
12
−++
+
+
+
+ T
TTT
T
T
RR
R abA
A)babAa
AAabA
aA)Ab
()(
(
+−−
+
+
A)bb
abAbbA
aAa
abAaaA
(
)(
)(
)(
R
R
R
R
T
TTT
TT
TTT
aAa
AaaA
AA
A)babAa
abAabA
aA)Ab
)(
)(
()(
(
TT
TT
TTT
TT
T
RRR
R
+
+
+
+
+
+
−=+
,
де використані властивості
TTT
R )()()(
+++
== AAAAAA ,
TT
bAAb =
+
(
відповідно
до
(2.11) ),
1
−=
+
aAb
T
(
відповідно
до
(2.12) ).
Наслідок 8.
Якщо
виконуються
умови
теореми
3,
то
TTT
∆∆+∆+∆=∆
+++
)()(
2
AAba,,AA,
, (2.16)
де
∆
визначається
по
формулі
(2.14).
При
доведенні
теореми
3
використовується
наступна
лема
.
Лема.
Квадратна
матриця
T
n
αβ
+
I
при
наявності
умови
1−=
βα
T
має
наступну
псевдообернену
матрицю
( )
−
−=+
22
β
ββ
α
αα
αβ
T
n
T
n
T
n
III
. (2.17)
Ця
лема
буде
використана
нижче
для
обчислення
збурень
у
псевдооберненій
матриці
,
якщо
під
збуреннями
початкової
матриці
розуміти
видалення
з
неї
деякого
її
стовпця
або
рядка
.
Випадок
4.
Нехай
мають
місце
умови
(2.11)
0)(
=aAa
TT
Z , 0)(
=bAb
TT
Z
але
при
цьому
не
виконується
рівність
(2.12),
тобто
1
−≠
+
aAb
T
. (2.18)
Тоді
,
як
це
випливає
з
доведення
теореми
3,
виконується
умова
AabA
rankrank
T
=+
)( . (2.19)
Теорема
4.
Якщо
для
матриці
nm
R
×
∈A
,
m
R
∈a
,
n
R
∈b
виконуються
умови
(2.11), (2.18),
то
мають
місце
співвідношення
−=−+=∆
+++
AabAba,,AA,
)()(
T
aAb
AabA
+
+
+
+
T
T
1
, (2.20)
Доведення цього твердження здійснюється перевіркою умов, яким
повинна задовольняти псевдообернена матриця.
Наслідок 9. Якщо виконані умови теореми 4, то
0)(
1
=∆
+
ba,,AA, . (2.21)
Наслідок 10. Якщо виконуються умови теореми 4, то
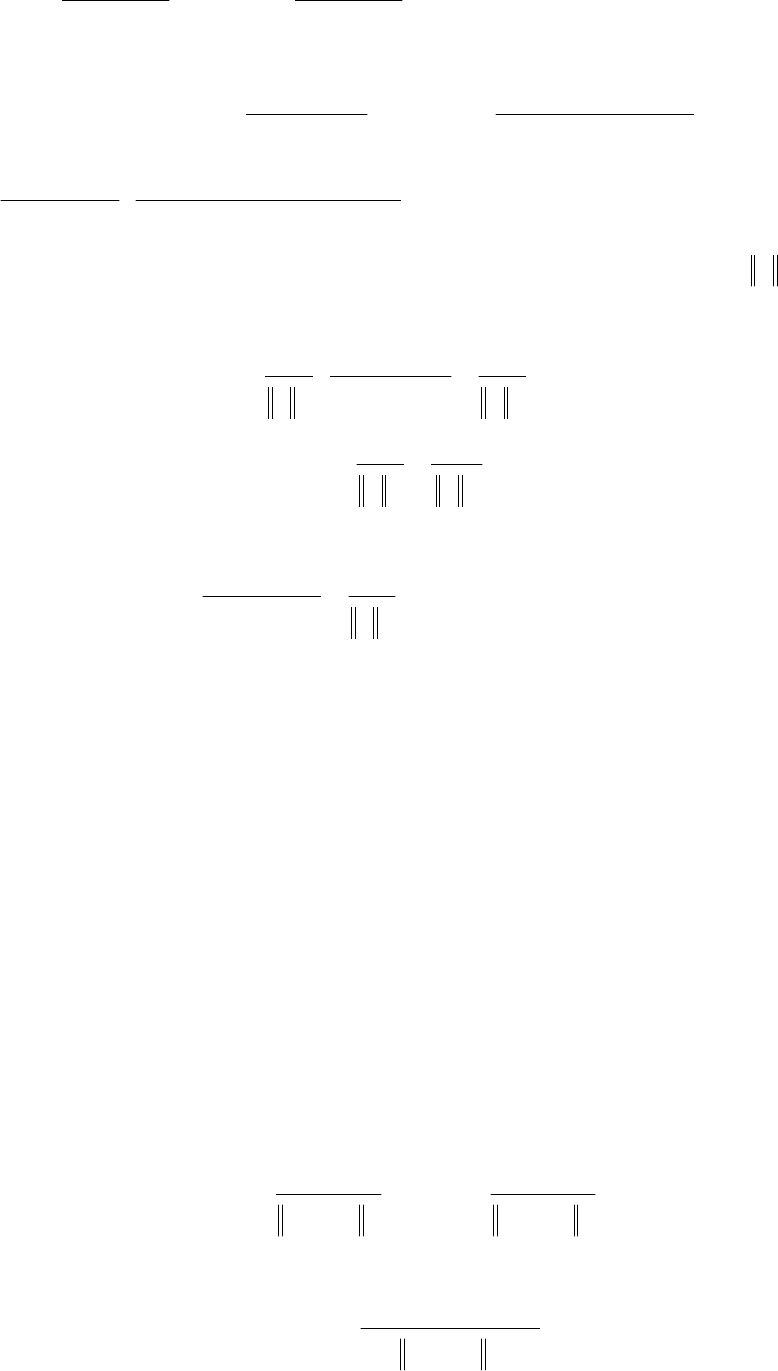
13
−−
++
=∆
++
+
++
+
+
AbaAAabA
aAb
A)bb
AaaA
aAb
ba,,AA,
TT
T
T
T
T
RR
R
)()(
1
(
1
1
)(
2
.(2.22)
Довести останню формулу можна наступним чином
=
+
−
+
−=+
+
++
+
+
++
+
aAb
AbaA
A
aAb
AabA
AabA
T
TTT
T
T
T
T
R
1
)()(
)(
1
)(
−−
++
+=
++
+
++
+
)(()(
1
)()(
1
1
)( AA)baAabA
aAb
AbaAabA
aAb
A
TT
T
TTT
T
RR
R
R .
Наслідок 11. Якщо
мають
місце
умови
теореми
2
і
2
( bA)bb <Z
T
,
1
−≠
+
aAb
T
,
то
+
+
++
+
−
+
−=∆ A
aAb
AabA
Iba,,AA,
22
1
)(
k
kk
k
kk
T
T
TT
n
, (2.23)
22
1
)(
d
dd
ba,,AA,
TT
k
kk
−=∆
+
, (2.24)
TTT
∆∆+∆+∆=∆
+++
)()(
2
AAba,,AA, , (2.25)
2
1
d
d
aAb
aA
−
+
=
+
+
T
k
,
A)b
d
(
Z
=
. (2.26)
Доведення
наслідку
11
випливає
з
розбивки
вектора
b
на
два
ортогональні
складові
A)bAbAb (Z+=
+
і
застосування
послідовно
до
матриці
T
)Aba(AAA
1
+
+=
теореми
4,
наслідку
9,
а
потім
до
матриці
T
Z )(( A)baA
1
+
наслідку
4
і
5.
Розглянемо
тепер
збурення
n
m
×
-
матриці
A
у
формі
або
поповнення
її
новим
рядком
до
встановлення
її
розмірності
n
m
×
+
)
1
(
або
вилучення
з
неї
однієї
з
її
рядків
із
зміною
розмірності
матриці
до
n
m
×
−
)
1
(
.
В
якості
збурень
без
обмеження
спільності
будемо
розглядати
поповнення
матриці
або
вилучення
останнього
рядка
.
При
поповненні
матриці
новим
рядком
для
визначення
збуреної
псевдооберненої
матриці
використовуються
добре
відомі
формули
Гревіля
[5]
Нехай
для
матриці
A
має
місце
співвідношення
0)( >aAa
TT
Z ,
тоді
−=
−−
++
+
22
(
(
(
(
A)a
A)a
Aa
A)a
A)a
A
a
A
Z
Z
Z
Z
T
T
Μ , (2.27)
2
(
)((
)(
A)a
AA)aaa
A
a
A
Z
ZZ
ZZ
T
T
−=
−− , (2.28)

14
+−−=−
−−
A)aa
AA)aa
A)aa
AA)aa
A
a
A
(
)((
(
)((
)(
Z
ZR
Z
RZ
RR
T
T
T
T
T
( )
)(1(
(
)((
2
A)aa
A)aa
AA)aa
R
Z
ZZ
T
T
T
++ (2.29)
якщо
0)( =aAa
TT
Z ,
то
++
−=
−−
++
+
A)aa
A)a
Aa
A)aa
A)a
A
a
A
(1
(
(1
(
R
R
R
R
T
T
T
T
Μ , (2.30)
)(A
a
A
ZZ
T
=
−− , (2.31)
A)aa
AA)aa
A
a
A
(1
)((
)(
R
RR
RR
T
T
T
+
−=−
−− . (2.32)
При
вилученні
з
матриці
−−
T
a
A
останнього
рядка
псевдообернена
і
проекційні
матриці
набувають
наступні
зміни
a)
при
1=qa
T
, (2.33)
де
)( qP
a
A
Μ=
−−
+
T
, (2.34)
P
a
aa
E
q
qq
EPqaEA
−
−=−=
++
22
)(
T
n
T
n
T
n
, (2.35)
2
)(
q
qq
a
A
A
T
T
ZZ +
−−= , (2.36)

15
×
−
−−
−
−=
222
)(
a
aa
E
a
A
a
aa
E
q
qq
EA
T
n
T
T
n
T
n
RR
4222
1
aq
q
a
q
q
a
q
qq
E
T
T
n
−
−
−× , (2.37)
b) при
1≠qa
T
, (2.38)
P
qa
qa
EPqaEA
−
+=−=
−+
T
T
n
T
n
1
)(
1
, (2.39)
−−=
T
ZZ
a
A
A)( , (2.40)
T
T
T
n
T
T
T
n
RR qq
qa
aq
E
a
A
qa
qa
EA −
−
+
−−
−
+=
11
)( , (2.41)
Слід
зазначити
,
що
умова
(2.33)
визначає
падіння
рангу
в
матриці
при
вилученні
вектор
-
рядки
T
a
,
тобто
1−
−−=
T
rankrank
a
A
A
, (2.42)
а
умова
(2.38) –
відсутність
зниження
рангу
−−=
T
rankrank
a
A
A
, (2.43)
Наведемо
доведення
формули
(2.35).
Якщо
)( qP
a
A
Μ=
−−
+
T
відома
матриця
,
де
q
–
її
останній
стовпчик
.
Тоді
,
відповідно
до
(2.27),
при
1=
qa
T
одержимо
PAa
A)a
A)a
A =−
++ T
Z
Z
2
(
(
, q
A)a
A)a
=
2
(
(
Z
Z
,
тобто,
(
)
PAqaI =−
+T
n
. Так як 1=qa
T
, то
(
)
0det =−
T
n
qaI і, відповідно до
(2.17)
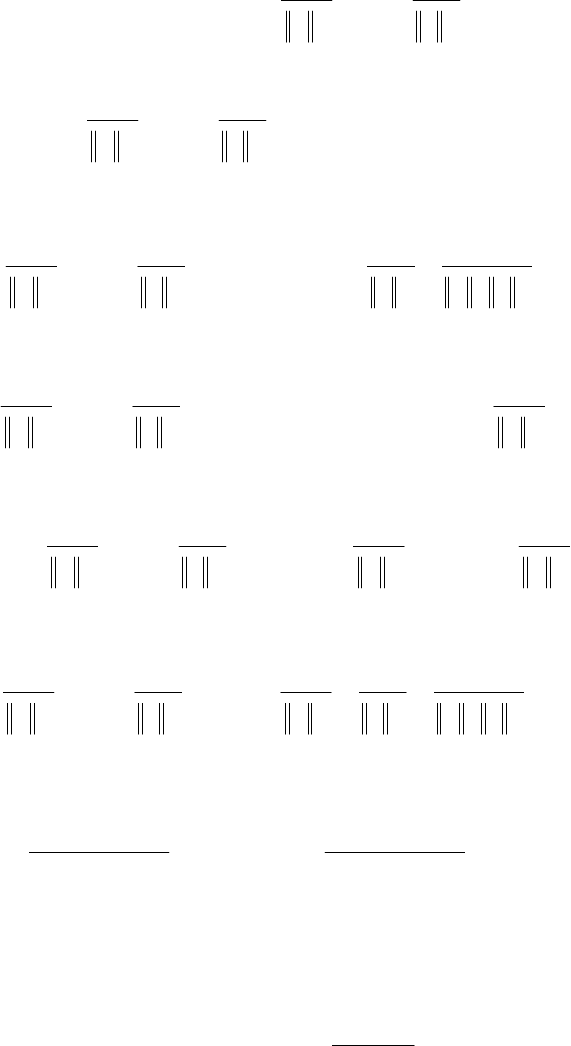
16
( )
P
a
aa
I
q
qq
IPqaIA
−
−=−=
+
+
22
T
n
T
n
T
n
,
=
−
−−
−−
−
−=
+
+ T
TT
T
n
T
n
qa
a
A
a
A
a
aa
I
q
qq
IAA
22
=−+
−−
−−
−
−=
+
22222
aq
qa
a
aa
a
A
a
A
a
aa
I
q
qq
I
TT
TT
T
n
T
n
222
q
qq
II
a
A
a
A
a
aa
I
q
qq
I
T
nn
TT
T
n
T
n
−+
−
−−
−−
−
−=
+
,
2222
)()(
q
qq
A
q
qq
a
A
a
aa
I
q
qq
IA
TT
T
T
n
T
n
ZZZ +=+
−−
−
−= .
Тут
використані
співвідношення
222222
aq
qa
a
aa
q
qq
I
a
aa
I
q
qq
I
TTT
n
T
n
T
n
+−−=
−
− .
Подібним
чином
доводиться
і
формула
(2.37).
Приведемо
доведення
формули
(2.39).
При
1≠qa
T
відповідно
до
(2.30)
q
A)aa
A)a
PAa
A)aa
A)a
A =
+
=
+
−
++
(1
(
,
(1
(
R
R
R
R
T
T
T
і з рівняння
(
)
PAqaI =−
+T
n
одержимо
( )
P
qa
qa
IPqaIA
−
−=−=
−
+
T
T
n
T
n
1
1
.
Формули
(40)
і
(41)
доводяться
простим
використанням
формули
(2.39).
3. Cинтез систем з оптимізацією модальних регуляторів
Розглянемо
задачу
оптимального
вибору
структури
розподілу
керуючого
сигналу
в
лінійній
системі
з
метою
мінімізації
норми
матриці
коефіцієнтів
підсилення
в
оберненому
зв
’
язку
закону
модального
регулювання
.
Нехай
в
системі

17
d t
dt
t t
x
Ax Bu
( )
( ) ( ),= + (3.1)
де
x
– n - вимірний, u – m - вимірний вектори, необхідно визначити
обернений зв’язок
u
C
x
(
)
(
)
t
t
=
(3.2)
згідно умови модального керування
det( )
λ λ λ
E A BC
n
n n
n
a a− − = + + +
−
1
1
Κ
(3.
3
)
при
оптимізації
C
за
рахунок
вибору
як
елементів
матриці
С
,
так
і
елементів
матриці
B
з
відповідних
множин
Ω
Ω
C B
, .
Методи
визначення
матриці
підсилення
модального
регулятора
наводяться
в
роботах
[2, 4, 6, 9, 11] .
Один
з
можливих
методів
визначення
матриці
модального
регулятора
зводиться
до
представлення
шуканої
матриці
у
вигляді
C vq=
T
[ 10, 11 ] .
Це
представлення
матриці
підсилення
звужує
множину
можливих
модальних
регуляторів
,
але
дає
можливість
порівняно
просто
визначати
коефіцієнти
модального
регулятора
.
Пропонується
наступний
підхід
по
визначенню
матриці
C .
Представимо
систему
(3.1)
у
вигляді
d t
dt
t u t u t u t
t
m m
T T
m m
T
x
Ax b b b
A b c b c b c x
( )
( ) ( ) ( ) ( )
( ) ( ),
= + + + + =
= + + + +
1 1 2 2
1 1 2 2
Κ
Κ
де
С
с
с
B b b u=
= =
1
1
1
T
m
T
m
m
t
u t
u t
Μ Κ Μ, ( , , ), ( )
( )
( )
.
Спочатку
розглянемо
систему
d t
dt
t u t
x
Ax b
( )
( ) ( )= +
1 1
і
визначимо
коефіцієнти
характеристичного
рівняння
det( )
λ
E A b c
n
T
− − =
1 1
0
по
формулі
[ 9 ]
p p P S b A c( ) ( ) ( ) ( , ( )) ,1 0 0 0
1 1
= −
T
де
p
p
A
A
(
)
,
(
)
,
0
0
=
=
елементами
вектора
p
є
коефіцієнти
характеристичного
рівняння
розімкнутої
системи
.
На
наступному
кроці
розглядається
система

18
d t
dt
t u t
T
x
A b c x b
( )
( ) ( ) ( )= + +
1 1 2 2
з коефіцієнтами характеристичного рівняння замкнутої системи
p p P S b A c( ) ( ) ( ) ( , ( )) ,2 1 1 1
2 2
= −
T
де
A A b c( ) ( ) .1 0
1 1
= +
T
На
кроці
m
розглядається
наступна
система
рівнянь
d t
dt
m t u t
m m
x
A x b
( )
( ) ( ) ( ) ,= − +1
де
A A b( ) ( ) ( ) ,m m u t
m m
−
=
−
+
− −
1 2
1 1
для
замкнутої
системи
,
якій
необхідно
забезпечити
наступні
коефіцієнти
характеристичного
рівняння
p a p P S b A c( ) ( ) ( ) ( , ( )) ,m m m m
T
m m
= = − − − −1 1 1
вибираючи
відповідним
чином
вектор
c
m
[ 9 ] .
Компоненти
вектора
a
T
n
a a a= ( , , , )
1 2
Κ
є
коефіцієнтами
характеристичного
рівняння
(3.3).
Таким
чином
,
у
випадку
обмежень
виду
с b
C Bj j
j j
∈
∈
Ω
Ω
( ), ( ),
наведена
задача
оптимізації
модального
регулятора
зводиться
до
наступної
задачі
керування
системою
з
дискретним
аргументом
p p P S b A c
A A b c
( ) ( ) ( ) ( , ( )) ,
( ) ( ) , , , , ,
k k k k
k k k m
T
k k
k k
T
+ = −
+ = + = −
+ +
+ +
1
1 012 1
1 1
1 1
Κ
(3.4)
з
початкового
стану
p
p
A
A
(
)
,
(
)
0
0
=
=
(3.5)
в
кінцевий
p a( )m
a
a
a
n
= =
1
2
Μ
(3.6)
при
умові
оптимізації
наступного
функціоналу
I
j j
j j j m
j
j
m
( , ) min .
( ), ( ), ,
c b c
b c
b c
=
∈ ∈ ∀ =
=
∑
Ω Ω 1
2
1
(3.7)
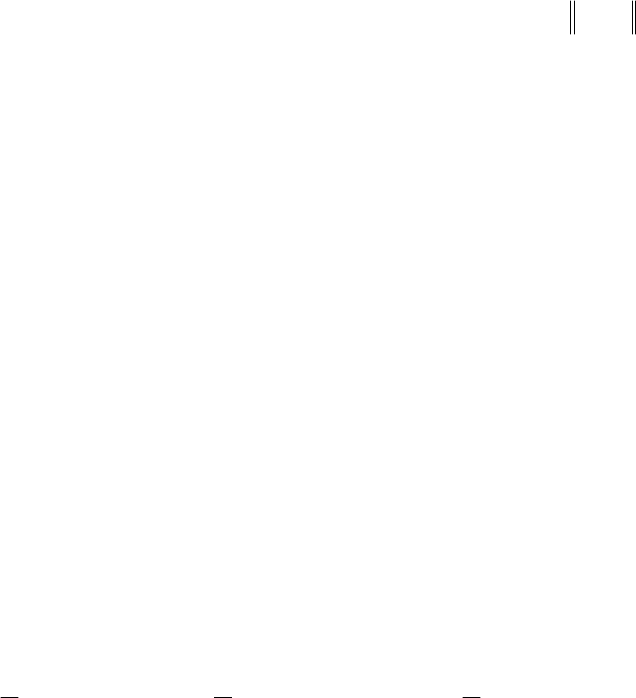
19
Вектор
p
T
n
p p p= ( , , , )
1 2
Κ
визначається
з
умови
det( ) ,
λ λ λ
E A
n
n n
n
p p− = + + +
−
1
1
Κ
P( )
( )
( ) ( )
( ) ( ) ( )
,k
p k
p k p k
p k p k p k
n n n
=
− − −
1 0 0 0
1 0 0
1 0
1
1
2 1
1 2 3
Κ
Κ
Κ
Λ Λ Λ Λ Λ
Κ
S b A b A b A b( , ( )) ( , ( ) , , ( ) ) .
k k k
n
k
k k k
+ + +
−
+
=
1 1 1
1
1
Κ
Для розв’язання поставленої задачі запишемо чисельну процедуру
знаходження матриць
C
B
i
.
З цією метою запишемо функцію
Гамільтона [12] для системи (3.4)
H k k k k k
k
( ( ), ( ), ( ), ( ), )p A cΨ Φ+ + =− +
+
1 1
1
2
[
]
[
]
+ + − + + +
+ + + +
Ψ Φ
T T
k k
T
k k
T
k k k k tr k k( ) ( ) ( ) ( , ( )) ( )( ( ) ) .1 1
1 1 1 1
p P S b A c A b c
Спряжені змінні
Ψ
Φ
(
)
,
(
)
k
k
задовільняють наступним системам
рівнянь
Ψ
( ) ( )
( )
k grad H
k
=
⋅
=
p
= −
+
+ + + + +
−
+
+ + +
−
+
+ +
E
c b c A b c A b
c b c A b
c b
n
k
T
k k
T
k k
T n
k
k
T
k k
T n
k
k
T
k
k k
k
k
0
0 0
0 0 0
0 0 0 0
1
1 1 1 1 1
2
1
1 1 1
3
1
1 1
( ) ( )
( )
( )
Κ
Κ
Λ Λ Λ Λ Λ
Λ
Λ
Ψ
Ψ
(
)
,
,
,
,
m
k
m
=
=
−
0
1
0
Κ
Φ
( ) ( )
( )
k grad H
k
=
⋅
=
A
(
)
= + − ×
+ + +
−
Φ( ) , ( ) , , ( )k k k
k
T
k
T
k
n
1
1 1 1
2
c A c A cΚ
( )
× + + +
+
+
+
−
E P E P E P
b
b A
b A
2 3
1
1
1
1 1 1
2
T T
n
T
k
T
k
T T
k
T T
k k k k k k
k
k
n
( ) ( ), ( ) ( ), , ( ) ( )
( )
( )
,Ψ Ψ ΨΚ
Μ
Φ
(
)
,
,
,
.
m
k
m
=
=
−
0
1
0
Κ

20
Матриці E
i
i n, ,= 2 розмірності
(
)
n
n
−
×
1
мають
наступну
структуру
E
e
e
e
E
e
e
E
e
2
2
3
3
3
4
0
0
0
=
=
=
T
T
n
T
T
T
n
n
T
Μ Μ
Κ
Μ
, , , ,
де
e
i
i n− = 2,
одиничні
орти
розмірності
n . Тоді
grad I grad H
i i
c c
c b
+ +
=
−
⋅
=
1 1
( , ) ( )
= + + − +
+ + +
2 1 1
1 1 1
c S b A P b
i i
T T
i
i i i i
( , ( )) ( ) ( ) ( ) ,Ψ Φ
grad I grad H
i i
b b
c b
+ +
=
−
⋅
=
1 1
( , ) ( )
`
(
)
= −
+ +
−
+ +
c A c A c P c
i
T
i
n
i
T
i
i i i i i
T
1 1
1
1 1
, ( ) , , ( ) ( ) ( ) ( ) ,Κ Ψ Φ
для градієнтних обчислювальних процедур
с c c b
b b c b
c
b
j j j
j j
j
grad I
grad I j m
j
j
= −
= − =
ρ
ρ
( , ) ,
( , ) , , , , .1 2 Κ
Після знаходження нових параметрів, в результаті градієнтного спуску,
c b
jj
j m, , ,=1 значення функціоналу (3.7) зменшиться, але при цих
параметрах кінцева умова (3.6) не буде виконуватися. Для коректування
параметрів, при яких буде задовольнятися кінцева умова (3.6), пропонується
наступна процедура. Ліанеризуємо систему (3.4) в околі векторів
c p
j i
j m k i n k m, , , ( ), , , , ,= = − = −1 1 1 0 1 в результаті для приростів
отримаємо наступну систему рівнянь
∆ ∆p E
b c
b A c b c
b A c b A c b c
p( )
( )
( ) ( )
( )k
k
k k
k
k
T
k
k
T T
k k
T
k
k
T T
k k
T T
k k
T
k
n n
+ = −
−
+ +
+ + + +
+ + + + + +
− −
1
0 0 0 0
0 0 0
0 0
0
1 1
1 1 1 1
1 1 1 1 1 1
2 3
Κ
Κ
Κ
Λ Λ Λ Λ Λ
Κ
−
− −
+
+
+
+
+
−
1 0 0
1 0
0
1
1
2 1
1 2
1
1
1
1
1
2
1
Κ
Κ
Κ
Λ Λ Λ Λ
Κ
Μ
p k
p k p k
p k p k
k
k
k
n n
k
T
k
T T
k
T T
k
T T
k
n
( )
( ) ( )
( ) ( )
( )
( )
( )
,
b
b A
b A
b A
c∆
