Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

7.2. The Strong Ergodic Theorem 155

0.5

1.5

210

240

270

120

300

150

330

180 0

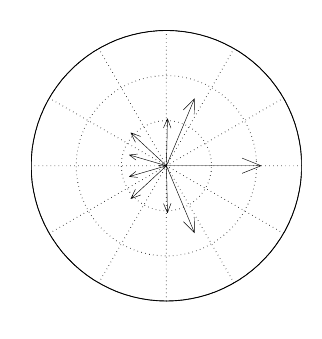
Figure 7.1. The eigenvalue spectrum for the projection matrix for the United

States population in 1966, plotted in the complex plane. The dominant eigenvalue

is λ

=1.0498.

Figure 7.1 shows the eigenvalue spectrum plotted in the complex

plane. (The computation of eigenvalues and eigenvectors is discussed

in Section 7.4.)

The largest eigenvalue is real and positive. The second largest is a

complex conjugate pair at angles of about θ = ±0.37π in the complex

plane. This pair would generate oscillations with a period 2π/θ ≈

5.4 projection intervals. Since the projection interval is 5 years, the

oscillation produced by this pair of eigenvalues has a period of 27

years.

7.2 The Strong Ergodic Theorem

A population is said to be ergodic if its eventual behavior is independent

of its initial state (Cohen 1979a). Ergodic theorems will appear repeatedly

throughout the following chapters. Most linear time-invariant matrix mod-

els are ergodic in a very strong sense of the word. Our understanding of

ergodicity relies on a powerful theorem about the eigenvalues of nonnega-

tive matrices. A matrix is nonnegative if all its elements are greater than

or equal to zero, and positive if all its elements are strictly greater than

zero. All population projection matrices are nonnegative, because negative

entries imply negative organisms, but they are not usually positive.

156 7. Birth and Population Increase from Matrix Population Models

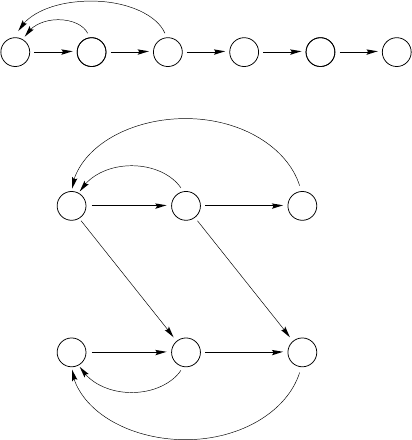
Reducible

Primitive Imprimitive

Irreducible



Nonnegative

Figure 7.2. The properties of nonnegative matrices.

7.2.1 The Perron–Frobenius theorem

A set of results known collectively as the Perron–Frobenius theorem de-

scribes the eigenvalues of nonnegative matrices. Two additional properties

of the matrix are important for this theorem: irreducibility and primitivity.

Nonnegative matrices can be divided into reducible and irreducible matri-

ces; irreducible matrices in turn are divided into primitive and imprimitive

matrices (Figure 7.2).

To deﬁne these terms, we need to deﬁne some structures in the life cycle

graph. A path from N

to N

is a sequence of arcs, traversed in the direction

of the arrows, beginning at N

and ending at N

, and passing through no

node more than once. A loop is a path from a node to itself. The length of

a path or a loop is the number of arcs it contains. A self-loop has length 1.

Thus, for example, the life cycle graph in Figure 3.9(a) contains three loops

(of length 2, 3, and 4) and no self-loops. The sequence N

→N

is a

path of length 2 from N

to N

. The sequence N

→N

is not a path, because it passes through N

twice.

7.2.1.1 Irreducibility

A nonnegative matrix is irreducible if and only if its life cycle graph contains

a path from every node to every other node (Rosenblatt 1957, Berman

and Plemmons 1994). Such a graph is said to be strongly connected. A

reducible life cycle contains at least one stage that cannot contribute, by

any developmental path, to some other stage or stages. A reducible matrix

can always be rearranged, by renumbering the stages, into a normal form:

A =



C D



, (7.2.1)

where the square submatrices B and D are either irreducible or can them-

selves be divided to eventually yield a series of irreducible diagonal blocks

(Gantmacher 1959, Berman and Plemmons 1994).

Most life cycle graphs are irreducible. One common exception (Fig-

ure 7.3a) occurs in life cycles with postreproductive age classes, which

cannot contribute to any younger age class (e.g., the killer whale life cy-

7.2. The Strong Ergodic Theorem 157

321

654

Habitat 1

Habitat 2

421

5 6

(a)

(b)

Figure 7.3. (a) An age-classiﬁed population with postreproductive age classes.

The corresponding matrix is reducible, because postreproductive age classes

cannot contribute to any younger age class. (b) A source-sink metapopula-

tion; the resulting matrix is reducible because individuals in Habitat 2 make

no contribution to any stage in Habitat 1.

cle in Figure 3.10). Another exception might arise in spatially structured

populations with one-way dispersal patterns (a “source-sink” model). Fig-

ure 7.3b shows an example; Habitat 1 contributes individuals to Habitat 2,

but not vice versa.

7.2.1.2 Primitivity

An irreducible nonnegative matrix A is primitive if it becomes positive

when raised to suﬃciently high powers, i.e., if A

is strictly positive for

some k>0. A reducible matrix cannot be primitive, because when the

matrix in (7.2.1) is raised to powers, the upper-right block remains zero.

Primitivity can be evaluated from the life cycle graph; a graph is primi-

tive if it is irreducible and the greatest common divisor of the lengths of its

loops is 1 (Rosenblatt 1957, Berman and Plemmons 1994). An imprimitive

matrix is said to be cyclic, and to have an index of imprimitivity d equal

to the greatest common divisor of the loop lengths in the life cycle graph.

The age-classiﬁed graph in Figure 3.9(a) has loops of length 2, 3, and 4; the

greatest common divisor of these lengths is 1, so the corresponding matrix

is primitive.

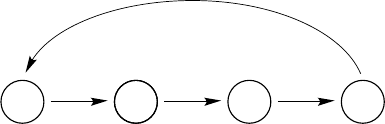
158 7. Birth and Population Increase from Matrix Population Models

421

Figure 7.4. An imprimitive life cycle graph for an age-classiﬁed population with

one ﬁxed age at reproduction. The graph contains only one loop, of length 4.

A suﬃcient condition for primitivity of an irreducible age-classiﬁed ma-

trix is the existence of any two adjacent age classes with positive fertility

(Sykes 1969, Demetrius 1971). For irreducible stage-classiﬁed models, a

suﬃcient condition for primitivity is the presence of at least one self-loop.

Most population projection matrices are primitive. The only signiﬁcant

exceptions are age-classiﬁed matrices with a single reproductive age class,

which might be appropriate for semelparous species such as monocarpic

perennial bamboos (Janzen 1976), periodical cicadas, or Paciﬁc salmon.

The life cycle graph for such an organism (Figure 7.4) contains only one

loop of length d,whered is the age of reproduction. Imprimitive matrices

also arise in models of annual plants (Chapter 13 of MPM).

7.2.1.3 Evaluating Irreducibility and Primitivity Numerically

It is easy to evaluate irreducibility and primitivity of small matrices by

inspection of the life cycle graph, but large matrices can be diﬃcult. Horn

and Johnson (1985, pp. 507–520) summarize several theorems that provide

numerical methods to evaluate irreducibility and primitivity. Suppose that

A is a nonnegative s × s matrix. Then

• A is irreducible if and only if (I + A)

s−1

is positive.

• Let c denote the length of the shortest loop in the life cycle graph of

A.ThenA is primitive if and only if A

s+c(s−2)

is positive. Since the

exponent increases with c, this result can be applied letting c be the

length of any loop in the life cycle graph.

• A is primitive if and only if A

−2s+2

is positive.

Thus, for example, a 20 × 20 matrix can be checked for irreducibility by

seeing if (I + A)

is positive. If the graph of A contains a loop of length 4,

A is primitive if and only if A

is positive. Without knowing the lengths

of any loops, the primitivity of A can be checked by seeing if A

342

is posi-

tive. The calculation of powers in these results is made easier by repeated

squaring of the matrix, i.e., calculating A

, A

, etc. The primitivity

7.2. The Strong Ergodic Theorem 159

of a 20 × 20 matrix can be evaluated by calculating A

512

using only nine

matrix multiplications.

Irreducibility and primitivity are determined by the arrangement of zero

and nonzero entries in the matrix; they are independent of the values of

those entries. Thus it is sometimes convenient to evaluate them using the

adjacency matrix of A, which has zeros in the same locations as the zeros

in A, and ones in those locations where A has positive elements. To avoid

overﬂow or underﬂow when raising matrices to high powers, rescale the

matrix to its adjacency matrix after each multiplication.

7.2.1.4 The Perron–Frobenius theorem

The Perron–Frobenius theorem

∗

describes the eigenvalues and eigenvectors

of a nonnegative matrix A. Its most important conclusion is that there

generally exists one eigenvalue that is greater than or equal to any of the

others in magnitude. Without loss of generality, we will call this eigenvalue

; it is called the dominant eigenvalue of A.

Primitive matrices: If A is primitive, then there exists a real, positive

eigenvalue λ

that is a simple root of the characteristic equation. This

eigenvalue is strictly greater in magnitude than any other eigenvalue.

The right and left eigenvectors w

and v

corresponding to λ

are

real and strictly positive. There may be other real eigenvalues besides

, but λ

is the only eigenvalue with nonnegative eigenvectors.

Irreducible but imprimitive matrices: If the matrix A is irreducible

but imprimitive, with index of imprimitivity d, then there exists a

real positive eigenvalue λ

which is a simple root of the characteristic

equation. The associated right and left eigenvectors w

and v

are

positive.

The dominant eigenvalue λ

is greater than or equal in magnitude to

any of the other eigenvalues; i.e.,

≥|λ

| i>1

but the spectrum of A contains d eigenvalues equal in magnitude to

.Oneisλ

itself; the others are the d − 1 complex eigenvalues

2kπi/d

k =1, 2,...,d− 1.

For example, if

A =

⎛

⎝

005

0.500

00.50

⎞

⎠

(7.2.2)

∗

For proofs, see Gantmacher (1959), Seneta (1981), or Horn and Johnson (1985).

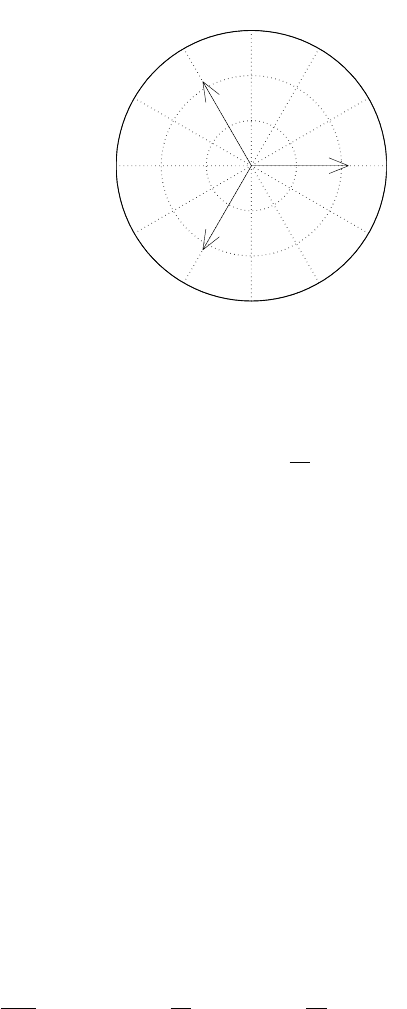
160 7. Birth and Population Increase from Matrix Population Models

0.5

1.5

210

240

270

120

300

150

330

180 0

Figure 7.5. The eigenvalue spectrum of the 3×3 imprimitive age-classiﬁed matrix

(7.2.2) with index of imprimitivity d =3.

the index of imprimitivity d = 3, and the eigenvalues are λ

=1.0772,

= −0.5389 + 0.9329i,andλ

= λ

. Figure 7.5 plots these three

eigenvalues in the complex plane.

Reducible matrices: If A is reducible, there exists a real eigenvalue λ

≥

0 with corresponding right and left eigenvectors w

≥ 0andv

≥ 0.

This eigenvalue λ

≥|λ

| for i>1.

The results of the Perron–Frobenius Theorem are summarized in Figure

7.6.

7.2.2 Population Growth Rate

The dominant eigenvalue λ

determines the ergodic properties of popula-

tion growth. Consider n(t) from (7.1.18):

n(t)=c

+ c

+ ···,

where the eigenvalues are numbered in order of decreasing magnitude. If

is strictly greater in magnitude than all the other eigenvalues, it will

eventually dominate all the other terms in (7.1.18). Regardless of the initial

population, the other exponential terms will eventually become negligible

and the population will grow at a rate given by λ

andwithastructure

proportional to w

. Dividing both sides by λ

yields

n(t)

= c

+ c





+ c





+ ···. (7.2.3)

7.2. The Strong Ergodic Theorem 161

Reducible

≥ 0

≥|λ

|, j>1

Primitive

> 0

> |λ

|, j>1

Imprimitive

> 0

= |λ

|, j =2,...,d

> |λ

|, j>d

Irreducible



Nonnegative

Figure 7.6. The relations among nonnegative, irreducible, and primitive matrices,

and a summary of the results of the Perron–Frobenius theorem.

If λ

> |λ

| for i ≥ 2, then taking the limit as t →∞yields

lim

t→∞

n(t)

= c

. (7.2.4)

This result is known as the strong ergodic theorem (Cohen 1979a); it

shows that, if A is primitive, the long-term dynamics of the population

are described by the population growth rate λ

and the stable population

structure w

. The growth rate λ

is related to the intrinsic rate of increase

r obtained from Lotka’s equation by λ

= e

or r =lnλ

The stable population structure is given by w

. Since eigenvectors are

determined only up to a scalar constant, w

can be scaled as desired, for

example, so that its elements sum to 1 and represent proportions, or so

that they sum to 100 and represent percentages. Writing the coeﬃcients

= v

∗

, as in (7.1.30), requires that whatever scaling is chosen satisﬁes

∗

=1.

7.2.2.1 The Stable Age Distribution

We can ﬁnd the stable age distribution directly from the Leslie matrix.

Writing Aw = λw,rows2–s give

= λw

162 7. Birth and Population Increase from Matrix Population Models

s−1

= λw

Since w can be scaled at will, let w

= 1, and then solve for successive

values. This gives the stable age distribution, with abundances of each age

class measured relative to the abundance of the ﬁrst:

= P

−1

= P

−2

= P

···P

s−1

−s+1

, (7.2.5)

which is directly analogous to (5.1.1),

corresponding to l(x)andλ

−i

corresponding to e

−rx

7.2.3 Imprimitive Matrices

An imprimitive matrix A has d eigenvalues with the same absolute mag-

nitude, where d is the index of imprimitivity. Only one of these eigenvalues

(λ

) is real and positive; the others form angles in the complex plane of

θ =2π/d, 4π/d,...,(d − 1)2π/d, and are thus either complex or, if d =2,

negative. The common magnitude of this set of d eigenvalues is strictly

greater than the magnitude of any of the remaining eigenvalues, so as

t →∞only the d leading eigenvalues have any inﬂuence on population

dynamics.

Cull and Vogt (1973, 1974, 1976) and Svirezhev and Logofet (1983) dis-

cuss the resulting dynamics in detail. Because of the complex eigenvalues,

the stage distribution does not converge, but instead oscillates with a pe-

riod d, as does the total population size. Suppose that d = 3, and consider

(7.2.3). The eigenvalues λ

and λ

are now complex, and |λ

| = |λ

| = λ

Using (7.1.31) for λ

, the limit (7.2.4) is replaced by

n(t)

→ c

+ c

(cos θt + i sin θt)w

+ c

(cos θt − i sin θt)w

(7.2.6)

as t →∞.Sincew

and w

and c

are complex conjugates, the

imaginary parts of (7.2.6) cancel out, so that n(t) is real, as it should be.

From (7.2.6) it follows that w

is still a stable stage distribution in the

sense that, if n(0) is proportional to w

,sothatc

= c

= 0, the population

will remain at that structure for all time. However, w

is not stable in the

sense that an initial population not proportional to w

will converge to it.

Instead, the limit in (7.2.6) is periodic, with period d.

Cull and Vogt (1973) show that a running average of n(t), with the

average taken over the period of the oscillation, converges to w

and grows

7.2. The Strong Ergodic Theorem 163

at a rate λ

lim

t→∞



j=1

n(t + j)

t+j

= c

(7.2.7)

The oscillatory asymptotic dynamics of imprimitive matrices makes in-

tuitive sense in the context of the life cycle graph. The existence of an index

of imprimitivity d>1 means that there is an inherent cyclicity in the life

cycle; all loops are multiples of some common loop length. This cyclicity is

reﬂected in the dynamics of the population.

7.2.4 Reducible Matrices

The dynamics generated by a reducible matrix A are aﬀected by initial

conditions. Rewrite A in normal form as

A =





. (7.2.8)

If B

and B

are reducible, they are further subdivided until we ﬁnally

arrive at

A =

⎛

⎜

⎝

··· ··· B

⎞

⎟

⎠

, (7.2.9)

where all the diagonal blocks are irreducible. Except for possible permuta-

tions of the block matrices, this decomposition is unique.

Let S

denote the set of stages in the submatrix B

. The stages in S

communicate with each other (because B

is irreducible), and may com-

municate with stages in S

i+1

,...,S

, but cannot communicate with the

stages in S

,...,S

i−1

. Since the dynamics of the stages in S

are indepen-

dent of the stages in any of the other sets, the irreducible matrix B

can be

analyzed by itself. Sometimes this makes biological sense, as the following

example shows.

Example 7.3 A population with postreproductive age classes

The matrix for a population with postreproductive age classes

(Figure 7.3a) can be put into normal form as





⎛

⎜

⎝

0 F

0000

0 P

0 00

00P

000

⎞

⎟

⎠

. (7.2.10)

164 7. Birth and Population Increase from Matrix Population Models

In this case, S

= {N

, N

} and S

= {N

, N

}. The irreducible

submatrix B

is the population projection matrix for the reproductive

age classes, while the submatrix B

contains the survival probabili-

ties of the postreproductive age classes. An analysis of B

alone will

give the growth rate of the reproductive part of the population. This

rate is unaﬀected by the postreproductive age classes, and the strong

ergodic theorem guarantees that the age distribution of this part of

the population will converge to stability.

Human demographers routinely truncate projections of the female

population at the end of the reproductive period. The 10 ×10 matrix

for the United States population in Example 7.2 is based on 5-year

age classes; it actually represents the submatrix B

, but the vital

rates of postreproductive females (over 50 years old) have no impact

on the eigenvalues.

If you choose instead to analyze the entire matrix A, the long-term

dynamics depend on the initial conditions. The dynamics of the popu-

lation in Example 7.3, for example, depend very much on whether the

initial population consists only of postreproductive females, or includes

some reproductive individuals.

More general cases can be more complicated. The sets of states S

de-

ﬁned by the partition of the life cycle generate a set of invariant subspaces

(Gantmacher 1959):

= S

+ ···+ S

(7.2.11)

= S

+ ···+ S

(7.2.12)

. (7.2.13)

m−1

= S

m−1

+ S

(7.2.14)

= S

. (7.2.15)

The subspaces are “invariant” because if the population lies in R

at time

t, it also lies in R

at time t + 1. The invariant subspaces are nested, so

⊂ R

m−1

···⊂R

The existence of more than one invariant subspace means that the pop-

ulation is not, strictly speaking, ergodic. The long-term dynamics are not

independent of initial conditions. A trajectory whose initial condition is

in R

but not in any of the larger subspaces R

,...,R

j−1

is trapped in

. It may or may not grow at the rate given by the dominant eigenvalue

of A. In Example 7.3 a population beginning with only postreproductive

individuals certainly does not do so.

An initial condition that lies in R

, but not in any of the smaller

subspaces R

,...,R

, contains individuals lying in each of the sets of

states S

,...,S

. The trajectory resulting from this initial condition will

eventually grow at the rate given by the dominant eigenvalue of A.