Jeanblanc M., Yor M., Chesney M. Mathematical Methods for Financial Markets
Подождите немного. Документ загружается.

560 10 Mixed Processes
Since the process L is a positive local martingale, it is a martingale if and
only if E(L
t
)=L
0
, ∀t. It suffices that
E
exp
sup
t≤T
t
0
ln(1 + γ
s
)dN
s
< ∞,
E
exp
sup
t≤T
t
0
ψ
s
dW
s
< ∞.
Comment 10.3.1.1 The study of uniformly integrable exponential martin-
gales in that setting can be found in many papers, including Cherny and
Shiryaev [169]andL´epingle and M´emin [580]. See also the list at the end of
this book in Appendix B.
10.3.2 Girsanov’s Theorem
From the representation theorem 10.2.6.1,ifP and Q are equivalent proba-
bilities, there exist two predictable processes ψ and γ, with γ>−1 such that
the Radon-Nikod´ym density L of Q with respect to P is of the form
dL
t
= L
t
−
(ψ
t
dW
t
+ γ
t
dM
t
) .
Then, from Theorem 9.4.4.1,
W and
M are Q-local martingales where
W
t
= W
t
−
t
0
ψ
s
ds,
M
t
= M
t
−
t
0
λ(s)γ
s
ds .
If γ is deterministic, the process N is a Q-inhomogeneous Poisson process
with deterministic intensity (λ(t)(1 + γ(t)),t ≥ 0) and
W and
M are Q-
independent. In the general case,
W and
M can fail to be independent as
shown in the following example.
Example 10.3.2.1 Suppose that the intensity of the Poisson process N is
equalto1andletdL
t
= L
t
−
γ
t
dM
t
,L
0
= 1 where γ is a non-deterministic
F
W
-predictable process. Denote by Q
γ
the probability Q
γ
|
F
t
= L
t
P|
F
t
.The
filtration of M
γ
is that of both M and
t
0
γ
s
ds, hence, the processes W and
M
γ
are not independent.
Comments 10.3.2.2 (a) Define Q|
F
T
= L
T
P|
F
T
,whereL follows (10.3.1)
with γ>−1. If E(L
T
) < 1 (this implies that L is a strict local martingale),
then Q is a positive finite measure on F
T
, but this measure is not a probability
measure.
(b) If L satisfies (10.3.1) and is a martingale without the condition γ>−1,
then the measure Q is no longer a positive measure. Nevertheless, one can
define a Q-martingale as a process Z such that ZL is a P-martingale. See
Ruiz de Chavez [748] and Begdhadi-Sakrani [65] for an extended study and
Gaussel [375] for an application to finance.

10.4 Mixed Processes in Finance 561
Exercise 10.3.2.3 Let (μ, σ, a
i
,i=1, 2) be given constants with a
i
> 0and
X
t
= μt+σB
t
+a
1
N
(1)
t
−a
2
N
(2)
t
where B is a BM and (N
(i)
,i=1, 2) are two
independent Poisson processes with respective intensities λ
i
.LetΨ be defined
by E(e
θX
t
)=e
tΨ(θ)
and Q|
F
t
= e
θX
t
−tΨ(θ)
P|
F
t
be a change of probability.
Let r be a given number.
Characterize θ such that (e
−rt+θX
t
,t≥ 0) is a Q-martingale.
This is a particular Esscher transform; see Subsection 11.3.1 for a more
general setting.
10.4 Mixed Processes in Finance
Bachelier [39] assumed that the dynamics of asset prices are Brownian motion
with drift, and Samuelson, in order to preserve positivity of prices worked with
the ordinary (or stochastic) exponential of drifted Brownian motion. Following
this idea, we introduce dynamics of prices as (stochastic) exponentials of
mixed processes (see Exercise 10.2.2.3). Let M be the compensated martingale
associated with a Poisson process N with deterministic intensity (λ(t),t≥ 0),
and W an independent Brownian motion. The dynamics of the price are
supposed to be given by
dS
t
= S
t
−
(b
t
dt + σ
t
dW
t
+ φ
t
dM
t
) (10.4.1)
where b, σ and φ are predictable processes. In a closed form
S
t
= S
0
exp
t
0
b
s
ds
E(σW)
t
E(φM)
t
.
The jumps of S occur when the process N jumps, and ΔS
t
= S
t
−
φ
t
ΔN
t
,
hence S
t
= S
t
−
(1 + φ
t
ΔN
t
). Therefore, in order that the price S remains
positive, we assume that φ>−1.
Note that the process
S
t
exp
−
t
0
b
s
ds
,t≥ 0
is a local martingale.
10.4.1 Computation of the Moments
In the constant coefficients case, with φ>−1, the solution of (10.4.1)maybe
written as
S
t
= S
0
exp
b − φλ −
σ
2
2
t + σW
t
+ [ln(1 + φ)]N
t
= S
0
e
X
t
(10.4.2)
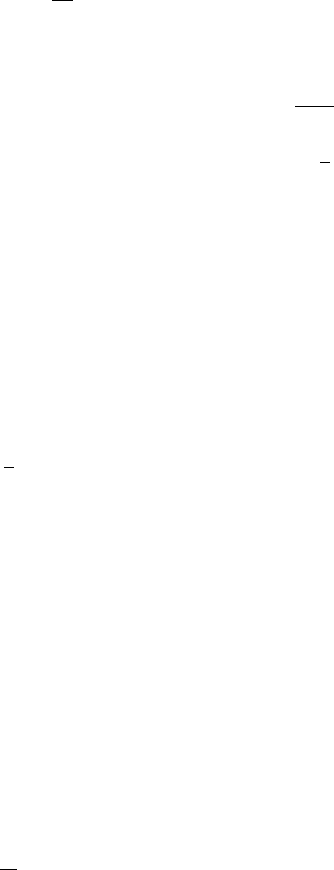
562 10 Mixed Processes
where X is the L´evy process (see Chapter 11 for information on
L´evy processes)
X
t
=
b − φλ −
σ
2
2
t + σW
t
+ [ln(1 + φ)]N
t
. (10.4.3)
The moments of the r.v. S
t
can be computed as follows: first, we have
e
−bt
S
t
k
= S
k
0
exp
k ln(1 + φ) N
t
− λkφt + σkW
t
−
tkσ
2
2
= S
k
0
E(φ
k
M)
t
E(σkW)
t
exp
t
λ[φ
k
− kφ]+
1
2
σ
2
k(k − 1)
where φ
k
=(1+φ)
k
− 1. Therefore,
S
k
t
= Z
(k)
t
exp(tg(k))
where we have denoted by Z
(k)
the martingale
Z
(k)
t
= S
k
0
E(φ
k
M)
t
E(σkW)
t
= S
k
0
exp(kX
t
− tg(k)) (10.4.4)
and g(k) is the Laplace exponent (see Subsection 11.2.3 for a generalization
to L´evy processes)
g(k)=bk +
1
2
σ
2
k(k − 1) + λ[(1 + φ)
k
− 1 − kφ] . (10.4.5)
Therefore, E(S
k
t
)=S
k
0
exp(tg(k)). In particular,
E(S
2
t
)=S
2
0
exp((2b + σ
2
+ λφ
2
)t) .
Note that, for every θ, the process exp(θX
t
− tg(θ)) is a martingale.
Exercise 10.4.1.1 Let S be given by (10.4.2). Give the dynamics of S
k
.
10.4.2 Symmetry
We present a put-call symmetry in the case where, under a domestic risk-
neutral probability Q, the dynamics of the process S are assumed to be,
dS
t
= S
t
−
((r − δ)dt + σdW
t
+ φdM
t
)
where M
t
= N
t
−λt is a Q-martingale and r, δ, σ, φ are constants with φ>−1.
Setting X
t
=(−φλ −
σ
2
2
)t + σW
t
+ [ln(1 + φ)]N
t
and Z
t
=exp(X
t
− tg(1)),
where g is defined in (10.4.5) and setting b = r − δ, one obtains
S
t
= S
0
e
(r−δ)t
Z
t
= S
0
e
(r−δ)t
exp(X
t
− tg(1))
where Z is a Q-martingale (see equality (10.4.4)).
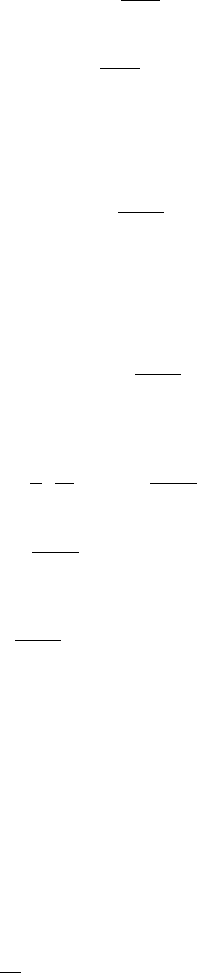
10.4 Mixed Processes in Finance 563
We can write
E
Q
(e
−rt
(K − S
t
)
+
)=E
Q
e
−δt
Z
t
KS
0
S
t
− S
0
+
= E
b
Q
e
−δt
KS
0
S
t
− S
0
+
,
where
Q|
F
t
= Z
t
Q|
F
t
. Under the foreign risk-neutral probability
Q,the
process Y =1/S follows (see Exercise 10.2.2.4):
dY
t
= Y
t
−
((δ − r)dt − σd
W
t
−
φ
1+φ
d
M
t
)
where
W
t
= W
t
− σt is a
Q-BM and
M
t
= N
t
− λ(1 + φ)t is a
Q-martingale.
Hence, denoting by C
E
(resp. P
E
) the price of a European call (resp. put) on
the underlying S with strike K,
P
E
(x, K, r, δ; σ, φ, λ)=C
E
K, x, δ, r; σ, −
φ
1+φ
,λ(1 + φ)
.
The same method establishes that American call and put prices satisfy
P
A
(x, K, r, δ; σ, φ, λ)=KxC
A
1
x
,
1
K
,δ,r,; σ,
−φ
1+φ
,λ(1 + φ)
.
Therefore, if b
p
(r, δ; φ, λ)(resp.b
c
(δ, r;
−φ
1+φ
,λ(1 + φ))) is the put (resp. call)
exercise boundary, then
b
p
(r, δ; φ, λ) b
c
δ, r;
−φ
1+φ
,λ(1 + φ)
= K
2
.
Comment 10.4.2.1 The put-call symmetry formulae for currency are well
known in the case of continuous processes (see e.g., Detemple [251]). Fajardo
and Mordecki [339] and Mordecki [659] establish, from the Wiener-Hopf
decomposition, a general symmetry relationship for L´evy processes. See also
Eberlein and Papapantoleon [293] and Eberlein et al. [294].
10.4.3 Hitting Times
We assume that the dynamics of the underlying process S
t
= S
0
e
X
t
are given
as in (10.4.2)by
S
t
= S
0
exp
b − φλ −
σ
2
2
t + σW
t
+ [ln(1 + φ)]N
t
.
564 10 Mixed Processes
Let us denote by T
L
(S) the first passage time of the process S at level L,for
L>S
0
, i.e.,
T
L
(S)=inf{t ≥ 0:S
t
≥ L}
and by T
(X)=T
L
(S) the companion first passage time of the process X at
level =ln(L/S
0
), for >0, i.e., T
(X)=inf{t ≥ 0:X
t
≥ }.
Assuming that the process S has no positive jumps, i.e., in the case where
φ ∈]−1, 0[, we apply the optional sampling theorem to the bounded martingale
(Z
(k)
t∧T
,t≥ 0) where Z
(k)
t
=exp(kX
t
−tg(k)) and k>0. Then, relying on the
continuity of the process S (hence of X) at the stopping time T
, we obtain
the following formula:
E[exp(−g(k)T
)] = exp(−k) .
Inverting the Laplace exponent g(k) we obtain the Laplace transform
E(exp(−uT
)) =
exp(−g
−1
(u) ), for >0
1 otherwise .
(10.4.6)
Here, g
−1
(u) is the positive root of g(k)=u. Indeed, the function k → g(k)
is strictly convex, and, therefore, the equation g(k)=u admits no more than
two solutions; a straightforward computation proves that for u ≥ 0, there
are two solutions, one of them is greater than 1 and the other one negative.
Therefore, by solving numerically the latter equation, the positive root g
−1
(u)
can be obtained, and the Laplace transform of T
is known.
If the jump size is positive, there is a non-zero probability that X
T
is
strictly greater than . In this case, we introduce the overshoot O
)
O
= X
T
− . (10.4.7)
The difficulty is to obtain the law of the overshoot. See Subsection 10.6.2
and references therein for more information on overshoots in the general case
of L´evy processes.
Exercise 10.4.3.1 (See Volpi [832]) Let X
t
= bt + W
t
+ Z
t
where W is
a Brownian motion and Z
t
=
N
t
k=1
Y
k
a(λ, F )-compound Poisson process
independent of W . The first passage time above the level x is
T
x
=inf{t : X
t
≥ x}
and the overshoot is O
x
= X
T
x
− x.LetΦ
x
be the Laplace transform of the
pair (T
x
,O
x
), i.e.,
Φ
x
(θ, μ, x)=E(e
−θT
x
−μO
x
1
{T
x
<∞}
) .
Let τ
1
bethefirstjumptimeofN. We wish to establish an integral equation
for Φ
x
using the following computation:

10.4 Mixed Processes in Finance 565
(1) Prove that
E(e
−θT
x
−μO
x
1
{T
x
<τ
1
}
)=e
(b−α)x
where α =
b
2
+2(θ + λ).
(2) Prove that
E(e
−θT
x
−μO
x
1
{T
x
=τ
1
}
)=
e
(b−α)x
α(μ − b + α)
[0,x[
(e
(α−b)y
− e
−μy
)F (dy)
+
1
α(μ − b − α)
[x,∞[
(e
(b−α)(y−x)
− e
−μ(y−x)
)F (dy)
+
e
μx
− e
(b−α)x
α(μ − b + α)
[x,∞[
e
−μy
F (dy)
+
e
(b−α)x
α(μ − b − α)
[0,∞[
(e
−(α+b)y
− e
−μy
)F (dy) .
(3) Prove that
E(e
−θT
x
−μO
x
1
{τ
1
<T
x
<∞}
)
=
1
α
R
F (dy)
(x−y)∧x
−∞
e
bz
(e
−α|z|
− e
(2x−z)α
)Φ
x−z−y
(θ, μ)dz .
(4) Deduce an equation for Φ by adding the three components above.
10.4.4 Affine Jump-Diffusion Model
These affine processes are defined as the solutions of the following equa-
tion (10.4.8):
Proposition 10.4.4.1 Suppose that
dX
t
= μ(X
t
)dt + σ(X
t
)dW
t
+ dZ
t
(10.4.8)
where μ and σ
2
are affine functions μ(x)=μ
0
+ μ
1
x ; σ
2
(x)=σ
0
+ σ
1
x and
Z is a ν-compound Poisson process such that
e
zy
ν(dy) < ∞, ∀z.Then,for
any affine function ψ(x)=ψ
0
+ ψ
1
x, for all θ, there exist two functions α
and β such that,
E
e
θX
T
exp
−
T
t
ψ(X
s
)ds
F
t
= e
α(t)+β(t)X
t
.
Proof: It suffices to prove the existence of α and β such that the process
e
α(t)+β(t)X
t
exp
−
t
0
ψ(X
s
)ds

566 10 Mixed Processes
is a martingale, and α(T )=0,β(T )=θ.FromItˆo’s calculus, this leads to a
Riccati ODE and to a linear ODE:
β
(t)=ψ
1
− μ
1
β(t) −
1
2
σ
1
β
2
(t) ,
α
(t)=ψ
0
− μ
0
β(t) −
1
2
σ
0
β
2
(t) − λ(ν(β(t)) − 1)
where ν(z)=
e
zy
ν(dy). It remains to check that there exists a solution
satisfying the boundary conditions.
Comment 10.4.4.2 See Duffie et al. [274, 272] for a generalization of this
model.
Exercise 10.4.4.3 Let λ(t, x)=λ
1
+ λ
2
x.Provethat
dX
t
= μ(X
t
)dt + σ(X
t
)dW
t
+ dM
t
where M is the compensated martingale of an inhomogeneous Poisson process
with intensity λ(t, X
t
) has a solution.
Hint: Start from the previous process (10.4.8) and make a change of
probability.
A Particular Case
As an example, let us study the case where S is an exponential of an affine
process with constant coefficients (see Exercise 10.2.2.3).
Proposition 10.4.4.4 Let W be a Brownian motion and Z a ν-compound
Poisson process independent of W of the form Z
t
=
N
t
n=1
Y
n
.Let
dS
t
= S
t
−
(μdt + σdW
t
+ dZ
t
) , (10.4.9)
where μ and σ are constants. The infinitesimal generator of S is given by
Lf = ∂
t
f + xμ∂
x
f +
1
2
σ
2
x
2
∂
xx
f +
R
(f(x(1 + y),t) − f(x, t)) dν(y)
for f sufficiently regular. The process (S
t
e
−rt
,t ≥ 0) is a martingale if and
only if E(|Y
1
|) < ∞ and μ + λE(Y
1
)=r.
If Y
1
≥−1 a.s., the process S can be written in an exponential form as
S
t
= S
0
e
X
t
,X
t
= bt + σW
t
+ V
t
where b = μ −
1
2
σ
2
and V is the (λ,
F )-compound Poisson process
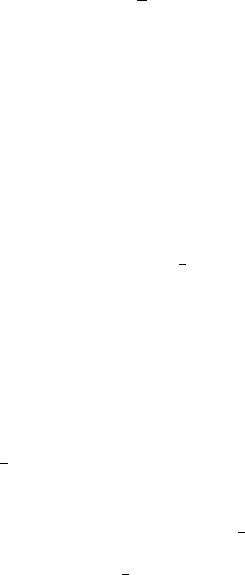
10.4 Mixed Processes in Finance 567
V
t
=
N
t
n=1
ln(1 + Y
n
)=
N
t
n=1
U
n
,
with
F (u)=F (e
u
− 1).
If moreover E(e
θU
1
) < ∞ for all θ,
E(S
θ
t
)=S
θ
0
e
tΨ(θ)
where
Ψ(θ)=θb +
1
2
σ
2
θ
2
− λ
∞
−∞
(1 − e
θu
)
F (du) .
Proof: The expression of the infinitesimal generator is straightforward, the
details are left to the reader. In order to give conditions which imply that
(S
t
e
−rt
,t≥ 0) is a local martingale, it suffices to write its dynamics as
d(e
−rt
S
t
)=e
−rt
S
t
−
((−r + μ + λE(Y
1
))dt + σdW
t
+ dZ
t
− λE(Y
1
)dt) ,
and to use the martingale property of the process (Z
t
− λE(Y
1
)t, t ≥ 0).
If Y
1
≥−1, the solution of (10.4.9)is
S
t
= S
0
e
μt
e
σW
t
−
1
2
σ
2
t
exp
N
t
n=1
ln(1 + Y
n
)
= S
0
e
bt+σW
t
+V
t
= S
0
e
X
t
with
X
t
= bt + σW
t
+ V
t
,V
t
=
N
t
n=1
ln(1 + Y
n
)
and b = μ −
1
2
σ
2
. Then, denoting by
F the cumulative distribution function
of ln(1 + Y
1
) (i.e.,
F (y)=F (e
y
− 1)), if E(e
θ ln(1+Y
1
)
) < ∞,
E(S
θ
t
)=S
θ
0
E(e
θX
t
)=S
θ
0
e
θbt
e
1
2
σ
2
θ
2
t
E(e
θV
t
)
= S
θ
0
e
θbt
e
1
2
σ
2
θ
2
t
exp
−tλ
∞
−∞
(1 − e
θu
)
F (du)
,
where the last equation follows from Proposition 8.6.3.4.
Example 10.4.4.5 We present two examples of jump-diffusion processes. We
assume that
X
t
= μt + σW
t
+
N
t
i=1
Y
i
where
N
t
k=1
Y
k
is a compound Poisson process.

568 10 Mixed Processes
• Merton’s Model. Merton [643] chooses a model where prices are of the
form S
t
:= xe
X
t
with X
t
= bt + σW
t
+
N
t
k=1
Y
k
where the law of Y
1
is
Gaussian, with mean μ and variance α
2
. In differential form
dS
t
= S
t
−
b +
1
2
σ
2
dt + σdW
t
+ dZ
t
with Z
t
=
N
t
k=1
Y
k
where the r.v’s
Y
n
are log-normal. In that case, the
density of the r.v. X
t
is easily obtained by conditioning on the number of
jumps, i.e., by N
t
= n,and
P(X
t
∈ dx)=e
−λt
∞
n=0
(λt)
n
n!
1
2π(σ
2
t + nα
2
)
e
−(x−bt−nμ)
2
/2(σ
2
t+nα
2
)
dx ,
Ψ(θ)=
1
2
σ
2
θ
2
+ bθ + λ(1 − e
−μθ+α
2
θ
2
/2
) .
• Kou’s Double-exponential Jumps Model. A particular jump-diffusion
model is the double exponential jumps model, introduced by Kou [540]and
Kou and Wang [541, 542]. In this model
X
t
= μt + σW
t
+
N
t
i=1
Y
i
,
where the density of the law of Y
1
is
ν(dx)=
pη
1
e
−η
1
x
1
{x>0}
+(1− p)η
2
e
η
2
x
1
{x<0}
dx .
Here, η
i
are positive real numbers, and p ∈ [0, 1]. With probability p (resp.
(1 − p)), the jump size is positive (resp. negative) with exponential law
with parameter η
1
(resp. η
2
). Then,
E(e
iuX
t
) = exp
t
−
1
2
σ
2
u
2
+ ibu + λ
pη
1
η
1
− iu
+
(1 − p)η
2
η
2
+ iu
− 1
,
and E(e
βX
t
)=exp(Ψ (β)t) is defined for −η
2
<β<η
1
where
Ψ(β)=βμ +
1
2
β
2
σ
2
+ λ
pη
1
η
1
− β
+
(1 − p)η
2
β + η
2
− 1
(in terms of L´evy processes (see Subsection 11.2.3), Ψ is the Laplace
exponent). Let T
x
=inf{t : X
t
≥ x}. Then, Kou and Wang [541] establish
that, for r>0, y>0, and x>0,
E(e
−rT
x
)=
η
1
− β
1
η
1
β
2
β
2
− β
1
e
−xβ
1
+
β
2
− η
1
η
1
β
1
β
2
− β
1
e
−xβ
2
,

10.5 Incompleteness 569
E(e
−rT
x
1
{X
T
x
−x>y}
1
{T
x
<∞}
)=e
η
1
y
η
1
− β
1
η
1
β
2
− η
1
β
2
− β
1
e
−xβ
1
− e
−xβ
2
,
E(e
−rT
x
1
{X
T
x
=x}
)=
η
1
− β
1
β
2
− β
1
e
−xβ
1
+
β
2
− η
1
β
2
− β
1
e
−xβ
2
and, for −η
2
<θ<η
1
E(e
θX
T
x
−rT
x
)=e
θx
η
1
− β
1
β
2
− β
1
β
2
− θ
η
1
− θ
e
−xβ
1
+
β
2
− η
1
β
2
− β
1
β
1
− θ
η
1
− θ
e
−xβ
2
where 0 <β
1
<η
1
<β
2
are roots of G(β)=r. The method is based
on finding an explicit solution of Lu = ru where L is the infinitesimal
generator of the process X.
10.4.5 General Jump-Diffusion Processes
Let W be a Brownian motion and p(ds, dz) the random measure associated
with a marked point process. Let F
t
= σ(W
s
,p([0,s],A),A ∈E; s ≤ t). The
solution of
dS
t
= S
t
−
μ
t
dt + σ
t
dW
t
+
R
ϕ(t, x)p(dt, dx)
can be written in an exponential form as
S
t
= S
0
exp
t
0
μ
s
−
1
2
σ
2
s
ds +
t
0
σ
s
dW
s
N
t
n=1
(1 + ϕ(T
n
,Z
n
))
where N
t
= p((0,t], R) is the total number of jumps on the time interval [0,t].
See Bj¨ork et al. [103] and Mercurio and Runggaldier [640] for applications to
finance.
10.5 Incompleteness
We consider a financial market with finite horizon T , where a risky asset with
price S is traded as well as the savings account, with deterministic interest rate
(r(t),t≥ 0). We denote by R(t) the discount factor R(t) = exp
−
t
0
r(s)ds
.
The natural filtration of S is denoted by F. In an incomplete arbitrage free
market, the set Q of e.m.m’s contains several equivalent probability measures
and perfect hedging is not possible. More precisely, pricing a contingent claim
H using an e.m.m. Q as E
Q
(R(T )H) does not correspond to the initial price
of a hedging strategy. However, trading the contingent claim H at price
E
Q
(R(T )H)forsomeQ ∈Q, does not induce an arbitrage opportunity. Due
to the convexity of the set Q of e.m.m’s, the set {E
Q
(R(T )H), Q ∈Q}is an
