Jan Svoboda. Magnetic Techniques for the Treatment of Materials

Подождите немного. Документ загружается.

170 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

In the third phase the particle begins to accelerate as it slips on the drum

surface. The radial component of the force of gravity decreases in this region

until the centrifugal force exceeds the radial force and the particle leaves the

drum:

= Y



(U + e)=I

+ I

(3.29)

Equations of motion of a particle on a magnetic drum in these three phases were

developed by Murariu [M14]. The equation of particle motion in the ﬁrst phase

can be written



U + e

sin  + 

U + e

cos   (

g

)



(U + e)

(3.30)

In the second phase the equation of motion is:



=0and thus

g

= $

(3.31)

In phase three the equation of motion becomes:



U + e

sin   

U + e

cos   (

g

)



(U + e)

(3.32)

with initial conditions:

 = 

(3.33)

g

= $

(3.34)

where 

is the angle of the slip point at the end of phase 2. At a certain value

of the angle ,denotedby

, the particle leaves the drum. At that moment

[M14]:



(U + e)(

g

)

= 

j cos  + I

(3.35)

It should be mentioned that in the case of the roll, the ﬁrst phase is absent

since a particle is deposited on the roll at the speed of the roll.

3.2.2 Motion of the particle after it leaves the roll

When the particle leaves the roll or the drum, it is being acted upon by the

force of gravity and by the magnetic force. Schematic diagram of this situation

is shown in Fig. 3.5. The equations of motion, in Cartesian coordinates, are

[M14]:

{

= 



{

({

+ |

)

1@2

(3.36)

= j 



({

+ |

)

1@2

(3.37)

3.2. PARTICLE MOTION IN DRUM AND ROLL SEPARATORS 171

=Ȧ

(

R+b

)

Figure 3.5: Forces acting on a particle when it has left the drum.

where the magnetic force is given by:

= 



e

exp

2n

(({

+ |

)

1@2

)  e  U

exp

2n

(({

+ |

)

1@2

)+e  U

(3.38)

Dierential equations (3.36) and (3.37) obey the following initial conditions

{(w =0)=(U + e)sin

(3.39)

|(w =0)=(U + e)cos

(w =0)=$

(U + e)cos

(w =0)=$

(U + e)sin

In equations (3.39) the term $

(U + e) represents the initial velocity of

the particle at the moment when it leaves the drum, while $

is the angular

velocity of the particle at that moment. By solving the equations of motion

(3.36) and (3.37), trajectories of particles can be obtained as a function of their

magnetic susceptibility, size, density and of the coe!cient of friction, magnetic

ﬁeld strength on the surface of the roll, the spatial distribution of the magnetic

ﬁeld and the angular velocity of the roll. An example of a family of particle

trajectories is shown in Fig. 3.6.

172 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Figure 3.6: Particle trajectories in a roll magnetic separator. Roll diameter:

76 mm, speed of rotation: 200 rpm, particle size: 2 mm and par-

ticle mass magnetic susceptibilities (from right to left): 2.5×10

7

2.5×10

6

and 5×10

6

/kg.

3.3 Separation of particles by a suspended mag-

net

Suspended (or overband) magnetic separators have been used over many decades

to improve material purity and to protect processing machinery by removing un-

wanted iron and steel objects from conveyed bulk material. Although the design

procedures of such magnetic systems, that use either electromagnets or perma-

nent magnets are well established, the understanding of fundamental principles

for extraction of metal is inadequate and standards for selecting suitable sepa-

rators are inconsistent and often incorrect.

The common practice [A15, H13] is to base the evaluation of a magnetic

separator on the so-called ”force index”, which is essentially the magnetic force

density acting on a ferromagnetic body to be removed from a stream of material.

Such an approach requires that, for the extraction to occur, the product of the

magnetic induction and its gradient assumes a certain minimum value

Although such a concept is valid for certain special shapes of bodies, it does

not, in general, describe correctly the behaviour of ferromagnetic particles in a

magnetic ﬁeld and can lead to erroneous design of a magnetic circuit.

3.3. SEPARATION OF PARTICLES BY A SUSPENDED MAGNET 173

3.3.1 Magnetic force in a suspended magnet

A starting point in the evaluation of the e!ciency of a suspended magnet is the

requirement that the magnetic force I

acting on a particle must be greater

than the sum of the competing forces, e.g. the force of gravity I

, the drag of

the environment I

, the force of friction I

and others. The magnetic force on

a ferromagnetic particle can be conveniently written as



=(

· u)



(3.40)

where 

is the eective magnetic dipole moment of the particle and E

is the

external magnetic induction.

When both the particle and the external medium are homogeneous and

isotropic, and the body has an ellipsoidal shape, the eective dipole moment is

[L3]



= Y





 



+ Q(

 

)

(3.41)

where K

is the external magnetic ﬁeld strength, 

and 

are the relative

magnetic permeabilities of the particle and the external medium, respectively,

Q is the demagnetization factor appropriate for the axis of the ellipsoid along

which K

is directed.

Using eqs. (3.40) and (3.41) we get for the magnetic force [S25]:



= Y



 



+ Q(

 

)

(



· u)



(3.42)

For a ferromagnetic body in a non-magnetic or weakly magnetic medium we

have 

AA 1 and 

=1, so that eq. (3.42) becomes:



= Y



 1



1+Q(

 1)

(



· u)



(3.43)

The relative magnetic permeability 

of the particle is the function of the

magnetic ﬁeld inside the particle, 

= 

(K), where [L3]



K =







+ Q(

 

)







1+Q(

 1)

(3.44)

for 



Q is the demagnetization factor appropriate for the axis of the easiest mag-

netization (i.e. the axis of the smallest Q), as the particle is assumed to be

oriented so that its axis is parallel to the external ﬁeld K

The expression (3.43) for the magnetic force is a product of two factors: the

ﬁrst factor reﬂects the physical properties of particles to be removed, while the

second factor, the magnetic force density



= u(



) (3.45)

174 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Table 3.1: Static force indices (FI) and their ratios for selected shapes [S25] (l -

length, d-diameter).

Object c@d Force index [10

6

1

] Ratio FI/FI

urg

Rod 1.0 29 889 7.4

4.0 9 515 2.4

10.0 4 037 1.0

Sphere 31 811 7.9

Plate

13×50×50 20 300 5.0

13×200×200 11 130 2.8

25×200×200 15 300 3.8

describes the properties of the magnetic system. It is this magnetic force density

that many designers call ”force index” and use to evaluate magnetic separators.

Let us assume that a particle to be extracted by a suspended magnet rests

on a stationary conveyor and that no burden of bulk material is present. In

equilibrium I

= I

, where



= Y

(

 

)j (3.46)

and 

is the density of the medium. Assuming that 

AA 

, and combining

eqs. (3.43), (3.45) and (3.46) Svoboda obtained [S25]:



= 

1+Q(

 1)



 1



j (3.47)

Equation (3.47) determines the minimum force density (or force index) required

to lift a stationary ferromagnetic body of relative magnetic permeability 

density 

and demagnetization factor Q, from its position on a belt, in the

absence of a burden of bulk material.

It can be seen that this minimum magnetic force density is independent

of particle size and depends solely on its shape (through the demagnetization

factor), its magnetic properties (through the relative magnetic permeability)

and its density. Equation (3.47) also shows that the ratio of force indices for

various shapes is in the ratio of their demagnetization factors (provided that

Q(

 1) AA 1, which is satisﬁed for all shapes but very long rods or thin

plates, for which Q??1). Table 3.1 gives several examples of ratios of force

index

The minimum static force index (or magnetic force density) as a function

of the demagnetization factor, for a given material characterized by 

and 

in the absence of the burden has, therefore, general validity for any size of the

object to be lifted. Figure 3.7 shows such a dependence for steel (

= 7800

kg/m

, 

= 1000). It can be seen that, for instance, for a steel sphere (Q =

0.33) IL =0.03T

/m (80.8×10

@inch).

3.3. SEPARATION OF PARTICLES BY A SUSPENDED MAGNET 175

Figure 3.7: Magnetic force density (or force index), for steel, as a function of

demagnetization factor (adapted from [S25]).

For majority of objects that are encountered in practice, the assumption that

the external magnetic ﬁeld is directed along the axis of easy magnetization of

the body is invalid. Objects such as plates, rods or bolts usually rest on a con-

veyor belt with their axes of easy magnetization perpendicular to the direction

of the external magnetic ﬁeld. Demagnetization factors appropriate for such

orientations are high and large force densities (or force indices) are required to

lift the body towards the magnet.

3.3.2 Torque on a magnetizable body

Under the above mentioned circumstances, the role of the magnet should be

ﬁrst to re-orient the ferromagnetic body in such way that its long axis (the axis

of easy magnetization) is parallel with the direction of the external magnetic

ﬁeld. This is accomplished by exerting a torque on the body by the externally

applied magnetic ﬁeld.

The magnetic torque is given [L3, L4] by:



W = 



(3.48)

Since 

= Y



> where P

is the magnetization of the particle, eq. (3.48)

can be rewritten:



W = Y



(3.49)

Assuming a body of spheroidal shape, the torque is perpendicular to the

plane passing through the axis of symmetry of the body and the direction of

176 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Axis of symmetry

Figure 3.8: A ferromagnetic bar in a transverse external magnetic ﬁeld.

. The magnitude of the torque is given [L5] (by analogy with the torque on

a dielectric spheroid in an electric ﬁeld)[S25]:

W =

(

 

)

| 1  3Q | K

sin 2

(

+ Q(

 

)

¤£



+ 

 Q(

 

)

(3.50)

and for 



W =

(

 1)

| 1  3Q | E

sin 2

2

1+Q(

 1)

¤£

1+

 Q(

 1)

(3.51)

Here  is the angle between the direction of E

and the axis of symmetry of

the spheroid. It can be seen that the maximum torque occurs at  =45

.The

torque is directed in such a way that it tends to turn the axis of symmetry of

a prolate (i.e. Q?0.33) or oblate (QA0.33) spheroid parallel or perpendic-

ular to E

, respectively. Therefore, the torque tends to align the axis of easy

magnetization of the body along E

In equilibrium, the magnetic torque is balanced by the torque exerted by

the weight of the particle J

and by the weight of the burden J

.Wecanthus

write for a particle having a shape of a bar:

W =

jd(

+ 

(3.52)

where d and w and dimensions of the bar, as shown in Fig. 3.8, k is the height

of the burden of the material and 

is its bulk density.

Combining eqs. (3.51) and (3.52) we obtain, in equilibrium, [S25]:

sin 2 = dj(



)

(



 1

+ Q)(



 1

 Q)

| 1  3Q |

(3.53)

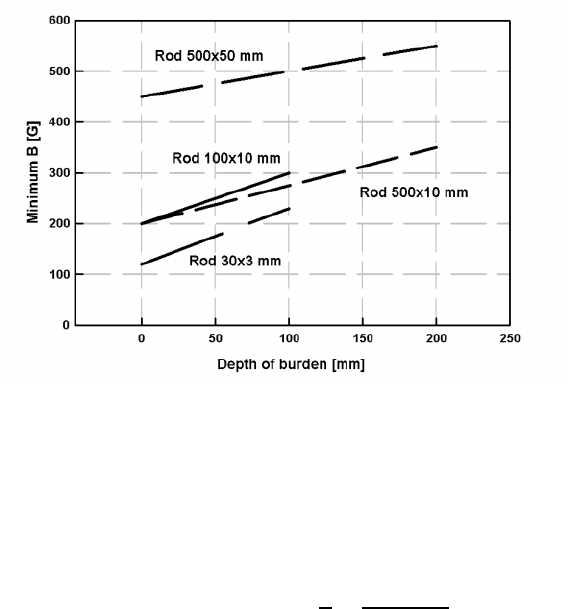
3.3. SEPARATION OF PARTICLES BY A SUSPENDED MAGNET 177

Figure 3.9: Minimum values of the magnetic induction, required to orient steel

rods of selected sizes, as a function of the depth of the burden

(adapted from Svoboda [S25]).

For 

AA 1 we then have:

sin 2



dj

(



)

Q(1  Q)

| 1  3Q |

(3.54)

It can be seen that if the magnetic system generates the ﬁeld that is per-

pendicular to the plane of the rod, the rod will not orient itself since  =90

and thus W = 0. It also transpires from eq. (3.48) that the gradient of the

magnetic ﬁeld does not contribute, in the ﬁrst approximation, to the torque.

Therefore, only the magnitude of the ﬁeld determines whether the reorientation

of the body takes place or not.

It is clear that in contrast to the conventional description of separation by

a suspended magnet, which requires that the magnetic system is designed in

such a way that the force index EuE achieves a certain minimum value, the

physical picture based on the magnetic torque approach requires a minimum

value of the magnetic ﬁeld only. The physical content of such a description can

have important implications for the design of the magnetic system.

It follows from the previous analysis that in a suspended magnet the im-

portant parameter is the magnetic ﬁeld strength. If the ﬁeld strength is high

enough so that it can orientate the body along the axis of easy magnetization,

the magnitude of the force index is required to be high enough to lift the parti-

cle in the direction of its axis of easy magnetization, only. Therefore, the force

index is not the only parameter needed to evaluate a suspended magnet.

For instance, the force index EuE may be just large enough to lift an

178 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Figure 3.10: Minimum values of the magnetic induction needed to orient steel

plates of selected sizes, as a function of the depth of the burden

(adapted from Svoboda [S25]).

object in the direction of its axis of easy magnetization, but the magnitude of

the magnetic ﬁeld itself may still be too low for the condition of eq. (3.53) to

be met. The object then will not re-orientate itself appropriately and will not

be lifted.

When designing the magnetic system of a suspended magnet two conditions

thus must be met: the magnitude and the direction of the magnetic ﬁeld must

satisfy eq. (3.54) and, at the same time, the force index must fulﬁll condition

given by eq. (3.47).

Typical dependence of the minimum magnetic ﬁeld on the depth of the

burden, for selected sizes of steel rods and plates, is shown in Figs. 3.9 and

3.10. Similar diagrams can be constructed for other shapes and sizes using eq.

(3.53), provided the demagnetization factors are known.

A comparison between theoretical values of the minimum magnetic induction

min

required to orient a body along its axis of easy magnetization, calculated

using eq. (3.53), and experimental values is given in Table 3.2. It can be seen

that the agreement is satisfactory.

3.3.3 Demagnetization factors

Calculation of the demagnetization factor for objects of shapes dierent from

that of an ellipsoid is complex and the values found in literature, e.g. for ellip-

soids and inﬁnite cylinders, are often of limited practical use. Brown [B3] gives

tables for circular cylinders of ﬁnite length, magnetized longitudinally, and for

3.3. SEPARATION OF PARTICLES BY A SUSPENDED MAGNET 179

Table 3.2: Comparison of theoretical and experimental values of the minimum

magnetic induction required to orient steel objects, as a function of

the depth of the burden [S25].

Object B

min

[T]

Burden depth [mm] Exp. Theor.

Rod 3×30 mm 0 0.0124 0.0113

10 0.016 0.0132

Plate 0.1×22×43 mm 0 0.0033 0.0034

10 0.0131 0.0114

Table 3.3: Demagnetization factors of ferromagnetic objects [S25]. Cylinders

and plates are magnetized longitudinally(l - length, d - diameter).

Object Size (c@g) N

Sphere 0.33

Finite cylinder 0 1.0

0.4 0.528

1.0 0.3116

4.0 0.098

10.0 0.041

40.0 0.011

100.0 0.004

1000.0 0.0004

Plate 13×50×50 mm 0.19

13×200×200 0.06

25×200×200 0.11

rectangular rods magnetized transversely. These geometries, together with an

ellipsoid, should be su!cient for analysis since other shapes usually encountered

in the separation practice (plates, hexagons) can be, in the ﬁrst approximation,

converted into geometries for which the demagnetization factors are available.

Values of demagnetization factors for selected shapes and sizes are given in Table

3.3.

3.3.4 The eect of the burden

It transpires from the above analysis that a ferromagnetic object to be lifted by

the suspended magnet must be ﬁrst re-orientated by the action of the magnetic

ﬁeld, in such a way that its long axis (i.e. the axis of easy magnetization) is

parallel with the direction of the magnetic ﬁeld. Once this is achieved, the

magnetic force is needed to overcome the weight of the object. The object will

then be lifted provided the force index acting on a particle is greater than the

minimum force index given by eq. (3.47).