Jan Svoboda. Magnetic Techniques for the Treatment of Materials

Подождите немного. Документ загружается.

160 CHAPTER 2. REVIEW OF MAGNETIC SEPARATORS

Figure 2.108: An automated hands-o two-stage ferrohydrostatic separator

(courtesy of De Beers Consolidated Mines (Pty.) Ltd.).

Figure 2.109: Ferrohydrostatic separator Rhomag

for separation of ﬁne par-

ticles (courtesy of De Beers Consolidated Mines (Pty.) Ltd.).

2.8. SEPARATORS WITH MAGNETIC FLUIDS 161

Feed

Flowguide

Magnet

Splitter Light fraction Heavy fraction

Magnetic fluid

Figure 2.110: Schematic diagram of the Magstream separator.

Figure 2.111: Magstream 200 separator.

162 CHAPTER 2. REVIEW OF MAGNETIC SEPARATORS

higher centrifugal and magnetic forces, at the same speed of rotation, overcome

displacement forces to move radially outwards. The separation density is then

given by:



= 

+ frqvw

(2.11)

where $ is the angular velocity. It can be seen that the additional degree of

freedom, namely the speed of rotation, can be used to control the separating

force acting on the particles.

The Magstream separators were available in several models, ranging from

laboratory-scale portable units for batch separation of samples up to 300 g, to

large continuous separators with a throughput up to 250 kg/h. Figure 2.111

shows the 200 Magstream model. Magstream separators can separate particles

over a range of densities from 1300 kg/m

to beyond 21 000 kg/m

.Theaccu-

racy of separation is claimed to be 100 kg/m

(0.1 g/cm

). For the most e!cient

separation, the sample should be sized between 60 m and 1 mm. Separation

of samples up to 4 mm is possible with special accessories.

Chapter 3

Theory of Processes of

Magnetic Separation of

Materials

In view of the diversity of magnetic separation techniques the theoretical de-

scriptions of the magnetic separation process are of limited general applicability.

So many factors may aect the behaviour of a system of particles that many

problems appear at ﬁrst sight to be of bewildering complexity. In general, the

particle motion in a non-homogeneous magnetic ﬁeld is so involved as to pre-

vent reasonable theoretical approach. On the other hand, however, a particular

problem can often be simpliﬁed considerably and a realistic appraisal of the

equations describing the motion of the particles is possible.

As has been mentioned in Chapter 1, a particle in a magnetic separator is

acted upon by a wide array of forces of various magnitudes and ranges. The

necessary (but not su!cient) condition for successful separation of more strongly

magnetic particles from less strongly magnetic particles is expressed by eq. (1.1).

In real situations, however, such a condition is di!cult to evaluate. The general

expression for the magnetic force (eq. (1.8)) acquires speciﬁc forms in dierent

types of magnetic separators, depending on the pattern of the magnetic ﬁeld

and its gradient. Also, the importance of various competing forces acting on

particles in a magnetic separator depends on the type of magnetic separator, on

the properties of the particles, such as size, shape, magnetic properties, density,

and on the type of ﬂuid in which the particles to be separated are suspended.

Workable models of material separation must, therefore, be developed sepa-

rately for individual types of magnetic separators. The situation is complicated

by the fact that many branches of magnetic separation, such as separation by

suspended magnets, magnetic pulleys or wet low-intensity drum magnetic sep-

arators still constitute highly empirical technology. Hesitant steps have been

taken to develop theoretical models of dry separation in roll and drum magnetic

separators. On the other hand, open-gradient magnetic separation, magnetic

163

164 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

ﬂocculation of weakly magnetic particles and wet high-gradient magnetic sep-

aration have received considerable theoretical attention. A notable number of

papers dealing with the problem of particle capture in HGMS led to an under-

standing of the interaction between a particle and a matrix element. However,

completely general treatment of the magnetostatic and hydrodynamic behav-

iour of an assembly of the ore particles in a system of matrix elements, in the

presence of a strong magnetic ﬁeld, is a theoretical problem of considerable

complexity.

A brief survey of the current theoretical descriptions of separation of ma-

terials in various types of magnetic separation equipment will be given in the

following sections.

3.1 The forces and the equations of particle mo-

tion

The equations of particle motion are relations between accelerations, velocities

and coordinates of the particles. They are second-order dierential equations

for the function u(w)> where u is the radius vector and w is the time. Their

integration makes possible, in principle, the determination of this function and

so of the path of the particles.

The equation of particle motion in a magnetic separator can be written in a

vector form as

d

= 



(3.1)

where p

d

is the inertial force, p

is the mass of the particle and d

its

acceleration. I

are all the forces that may be present in a magnetic separator,

such as the magnetic force, force of gravity, hydrodynamic drag, centrifugal

force, the friction force, surface forces, magnetic dipolar forces and electrostatic

forces among the particles and others. In order to be able to solve eq. (3.1), it

is necessary to evaluate the components of all its terms in suitable coordinates.

To obtain the components of the inertial force in polar coordinates that are

convenient for most types of magnetic separators, let us consider two mutually

perpendicular unit vectors ˆu and

= We shall assume that these vectors have

directions of increasing u and  and their directions change with time. Since

the derivative of a unit vector is perpendicular to the vector, the time rates of

ˆu and

 can be expressed as [G1]

gˆu

g

 (3.2)



= 

g

ˆu (3.3)

Now, the position of the particle, in polar coordinates, is given by u = uˆu.

Dierentiating this equation and using eqs. (3.2) and (3.3), the components of

3.1. THE FORCES AND THE EQUATIONS OF PARTICLE MOTION 165

the particle velocity y are found to be

(3.4)



= u

g

(3.5)

The subscripts u and  indicate the radial and azimuthal components, respec-

tively. By further dierentiation, the components of the particle acceleration d

are obtained and hence the components of the inertial force are [G1]

= 

 u

g

(3.6)

s

= 



g

(3.7)

In Cartesian coordinates these equations can be written as

= 

{

(3.8)

= 

(3.9)

Complete equations of motion are obtained by combining eq. (3.1) with eqs.

(3.6) and (3.7) or (3.8) and (3.9).

While it is fairly straightforward to express components of most of the com-

peting forces, such as the force of gravity and the hydrodynamic drag, the

magnetic force is more complicated. The general form of the components of the

magnetic force, in polar coordinates are given by:





+ E



) (3.10)







C

+ E



C

) (3.11)

In the Cartesian system the components of the magnetic force can be ex-

pressed as:

{





{

+ E

) (3.12)





{

+ E

) (3.13)

where 

is the volume magnetic susceptibility.

It can be seen that in order to use the above equations, we must be able to

specify the components of the magnetic induction and its gradient. Each type

of a magnetic separator generates its speciﬁc pattern of the magnetic ﬁeld and

the problem of particle motion has to be solved separately for each type of a

magnetic separator.

166 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Rotatin

drum

Permanent ma

nets

Figure 3.1: Arrangement of magnetic poles in a drum magnetic separator.

3.2 Particle motion in drum and roll separators

Drum and roll magnetic separators are characterized by periodic arrays of mag-

netic poles. Laurila [L2] made a fundamental investigation of the periodic mag-

netic ﬁeld of the cylindrical array of magnets with radial and axial poles used

in drum and roll separators. The general expressions for the components of

the magnetic force derived in [L2] can then be simpliﬁed in speciﬁc geometrical

arrangements of the magnetic poles.

Hopstock [H12] derived, based on mathematical and empirical analysis, ap-

proximate expressions for the radial and azimuthal components of the magnetic

ﬁeld around a magnetic drum with axial arrangement of the magnetic poles, as

shown in Fig. 3.1.

Magnetic force in a drum separator

The approximate expressions for the radial and azimuthal components of the

magnetic induction, derived by Hopstock [H12] are :

= E

cos(



)exp

(u  U)



(3.14)



= E

sin(



)exp

(u  U)



(3.15)

These equations were found to give a good ﬁt to experimental data in a num-

ber of dierent magnet conﬁgurations [H12]. The magnetic induction around a

drum, shown in Fig. 3.1, is then given by:

E = E

exp

(u  U)



(3.16)

3.2. PARTICLE MOTION IN DRUM AND ROLL SEPARATORS 167

Figure 3.2: Forces acting on a particle placed on a magnetic drum or roll.

where E

is the magnetic induction on the surface of the drum. It can be seen

that in this approximation E is independent of angle . The approximation is

most accurate when the following condition is met

u  U =





U (3.17)

The term on the right-hand side of eq. (3.16) expresses the depth of the ﬁeld,

deﬁned as a distance from the surface at which the ﬁeld is reduced to 1/h of its

surface value.

Equations (3.14) and (3.15) allow calculation of the magnetic ﬁeld gradi-

ent and thus the magnitude of the magnetic force. As a ﬁrst approximation,

Hopstock found that the radial component of the magnetic force, acting on a

magnetite particle in a drum magnetic separator is given by

3Y





(3.18)

Under Hopstock’s approximations, the azimuthal component of the magnetic

force is equal to zero, which is incorrect. In a more rigorous treatment by Birss

et al. [B9], accurate expressions for the components of the magnetic ﬁeld and

force were derived in the form of a Fourier series.

Whether or not a particle is held on the drum and carried to the magnetic

fraction depends on the relative magnitudes of the magnetic force and the grav-

itational and centrifugal forces. The forces acting on a particle situated on the

surface of a drum or a roll are shown in Fig. 3.2. For a given angle of rotation

168 CHAPT ER 3. THEORY OF MAGNETIC SEPARATION

Magnets

Figure 3.3: Arrangement of magnetic poles in a roll magnetic separator.

, the radial force acting of a particle can be expressed as:





+ Y



j cos   Y



U (3.19)

where $

is the angular velocity of the particle on a roll or drum of radius U.For

a speciﬁc case of a high-speed drum, when the force of gravity can be neglected,

the centrifugal force equals the magnetic force acting on a magnetite particle

when the drum is rotating at the critical angular velocity (in rad/s) given by

[H12]:

3E







1@2

(3.20)

Expressions for the components of the magnetic induction for a roll magnetic

separator, shown in Fig 3.3, can be written, in cylindrical coordinates, in a more

rigorous form [M14]:

= E

sin(

2



})exp



2



(u  U)

(3.21)

}

= E

cos(

2



})exp



2



(u  U)

(3.22)

where E

is the magnetic induction on the surface of the roll, U is the radius of

the roll and  is the periodicity of the magnetic system. The above equations

can be re-written in a more general form as [M14]:

= E

sin(n

})exp[n

(u  U)] (3.23)

}

= E

cos(n

})exp[n

(u  U)] (3.24)

where n

and n

are constants that describe the pattern of the magnetic ﬁeld

as a function of u and }. These constants can be determined, for instance, from

the electromagnetic modelling of a speciﬁc roll separator.

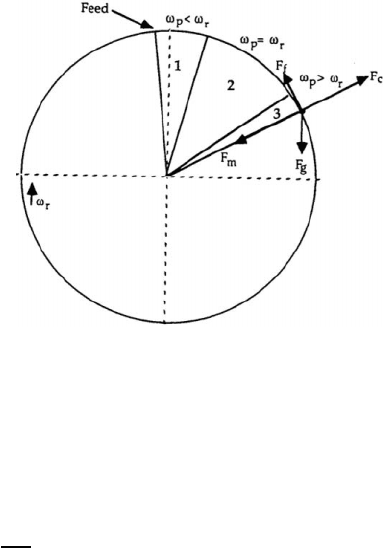
3.2. PARTICLE MOTION IN DRUM AND ROLL SEPARATORS 169

Figure 3.4: The forces acting on a particle in a drum magnetic separator

(adapted from [C9] and [S24]).

Magnetic force acting on a spherical particle of radius e and volume magnetic

susceptibility 

, on the magnetic roll or drum, can then be written as:

= 



e

{exp [2n

(u  e  U)]  exp [2n

(u + e  U)]} (3.25)

3.2.1 Motion of a particle on the drum or roll surface

The motion of a particle of radius e> situated on the surface of a drum separator

of radius U, can be divided into three phases [C9], as shown in Fig. 3.4. In

the ﬁrst phase, the particle is accelerating under the inﬂuence of the force of

friction I

and the tangential component of the force of gravity I

,givenby

the following equation:

= 

+ I

 I

) (3.26)

= jY



sin  (3.27)

where 

is the coe!cient of dynamic friction and the angle  is deﬁned in Fig.

3.2. The end condition of phase 1 was deﬁned by Cakir et al. [C9] as the point

when the particle reaches rotor speed $

, i.e. $

= $

Once the particle acquires the speed of the drum, a static friction coe!cient



, replaces the dynamic friction coe!cient in eq. (3.26). The particle then

moves with the constant angular velocity equal to the speed of the drum. When

the tangential component I

of the force of gravity (Fig. 3.2) becomes greater

than the force of friction I

, or when the particle leaves the drum, the motion

of the particle enters the third phase. At the end of the second phase

= 

+ I

 I

)=I

(3.28)