James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

10.3 Slowly rotating atmospheres

359

(a)

-?0S

-60S -30S 0 30N 60N 90N

LATITUDE

(b)

90N

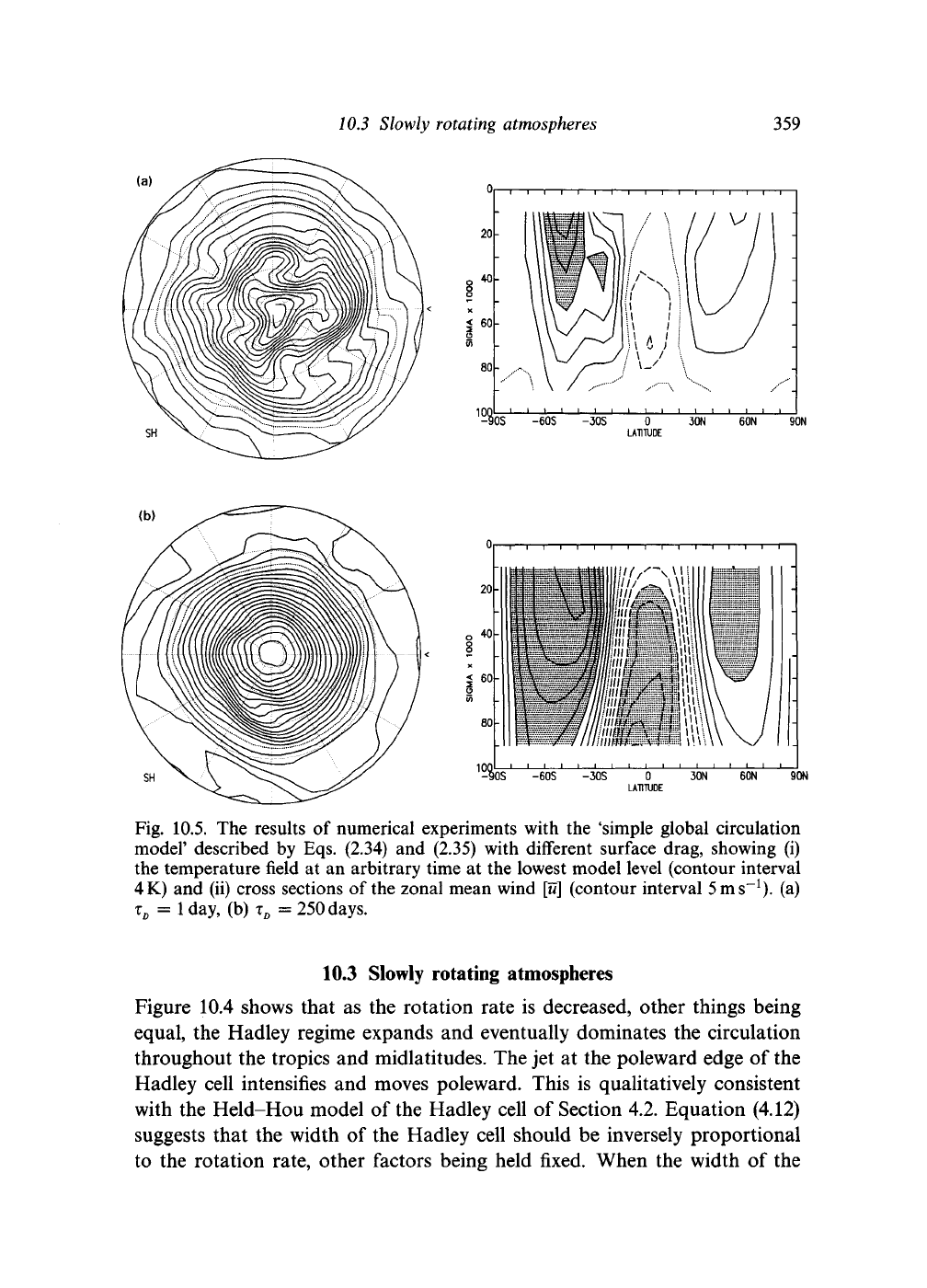
Fig. 10.5. The results of numerical experiments with the 'simple global circulation

model' described by Eqs. (2.34) and (2.35) with different surface drag, showing (i)

the temperature field at an arbitrary time at the lowest model level (contour interval

4K) and (ii) cross sections of the zonal mean wind

[u]

(contour interval

ms"

(a)

day, (b)

250

days.

10.3 Slowly rotating atmospheres

Figure 10.4 shows that as the rotation rate is decreased, other things being

equal, the Hadley regime expands and eventually dominates the circulation

throughout the tropics and midlatitudes. The jet at the poleward edge of the

Hadley cell intensifies and moves poleward. This is qualitatively consistent

with the Held-Hou model of the Hadley cell of Section 4.2. Equation (4.12)

suggests that the width of the Hadley cell should be inversely proportional

to the rotation rate, other factors being held fixed. When the width of the

360 Planetary atmospheres and other fluid systems

Hadley cell becomes comparable to the planetary radius, the Hadley cell will

dominate the circulation and more or less squeeze out the quasi-geostrophic

wave regime. The condition for a dominant Hadley cell is therefore

L <ia20)

The dimensionless number Ro

is simply a Rossby number, in which the

characteristic velocity scale has been estimated by assuming thermal wind

balance between the temperature and zonal wind field, and in which the

characteristic length scale is the planetary radius.

Pure angular momentum conservation, as assumed in Section 4.2, would

lead to very strong zonal winds at high latitudes, and a state of zero abso-

lute angular momentum throughout most of the midlatitudes and tropics.

Friction with the surface will moderate these strong winds, and will have

an increasing effect as the rotation rate decreases, so that the overturning

timescale of the Hadley cell becomes very long in comparison with the drag

timescale. Accordingly, in Fig. 10.4, the zonal winds do not exceed

ms"

when Q is one quarter that of the Earth, and they decrease for smaller Q.

Venus provides the best-studied example of a slowly rotating atmosphere

in the solar system. The atmosphere of Venus is dense and deep, but we

will largely concern ourselves with motions near the cloud top levels, about

km above the surface, where the pressure is around

kPa and where the

bulk of the incoming solar radiation is absorbed. A small fraction of the

incoming solar radiation reaches the surface, and it serves to maintain the

temperature gradients in the lower troposphere close to the adiabatic lapse

rate.

But measurements from descending probes suggest that the winds in

the lower troposphere are very small, and that the meteorologically active

layers are in the vicinity of the cloud tops, where very strong winds are

observed. The zonal component dominates, and is such that the cloud tops

superrotate, with the atmosphere circulating the planet once every 4 Earth

days or so. Relative to the solid planet, the equatorial winds are around

100

ms""

(They are in fact easterlies, but since Venus has a slow retrograde

rotation, they represent a superrotation.) The winds decline at lower and

higher levels; at latitudes higher than about 40°, the cloud tops are roughly

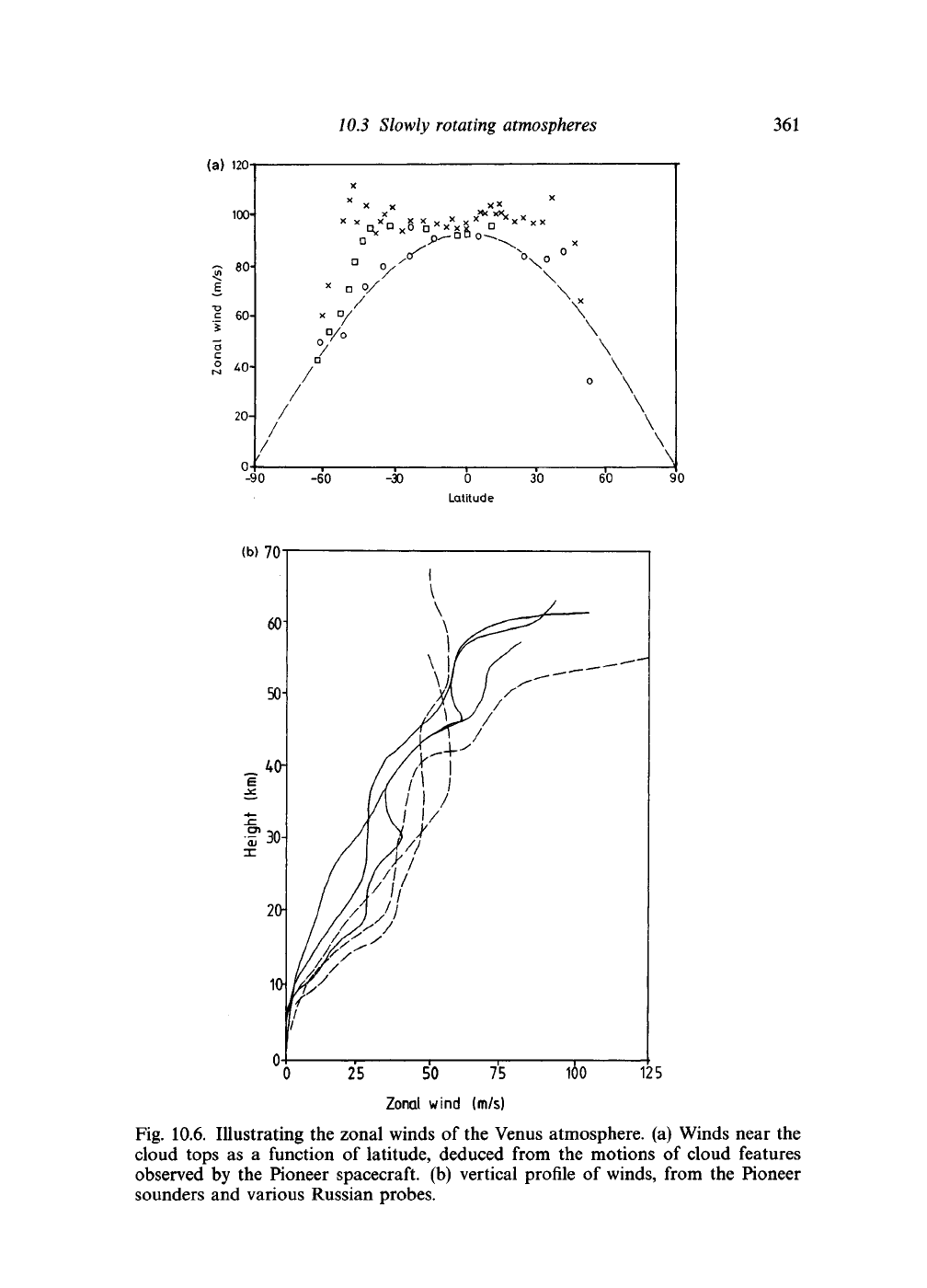
in solid body rotation about the poles. Figure 10.6 summarizes the observed

wind fields.

When the zonal winds are as strong as they are on Venus, the 'centri-

fugal force' acting on air parcels is appreciable. In the simplest case, the

horizontal component of the centrifugal force would be expected to balance

the remaining large force, namely the pressure gradient force. For steady,

10.3 Slowly rotating atmospheres 361

0) /[}

60-

50-

~ 40-

f—

•5 30-

20-

I/A

)

\ 1/

/\\

//\\ \

An/

1/1

A i

I j/'i/

/ AT '/

//''

25 50

/ .

160 12

Zonal wind (m/s)

Fig. 10.6. Illustrating the zonal winds of the Venus atmosphere, (a) Winds near the

cloud tops as a function of latitude, deduced from the motions of cloud features

observed by the Pioneer spacecraft, (b) vertical profile of winds, from the Pioneer

sounders and various Russian probes.

362

Planetary atmospheres

and

other fluid systems

frictionless motion, the zonal mean of Eq. (1.33b) reduces to

— tan

<j)

2Q[u]

sin

<j>

= -g^-, (10.21)

a oy

where pressure has been used as a vertical coordinate. When | [u] |> Qa,

the centrifugal term dominates over the Coriolis term, and so the meridional

momentum equation can be simplified yet further to a balance between

centrifugal force and pressure gradient force, called 'cyclostrophic balance',

described by:

A cyclostrophic thermal wind equation can be obtained from this relationship

by using the hydrostatic equation to eliminate the geopotential height. This

can be written:

tan0 8y

V ;

where h(p) was defined in Eq. (1.54). Note that cyclostrophic balance is not

possible for arbitrary temperature fields. Assume that

[u]

is close to zero at

the surface. Then at any arbitrary lower pressure

Clearly, if the integral on the right hand side of this equation were positive,

cyclostrophic balance would imply imaginary [u], and so a more complex

balance of forces must apply. A minimum condition for cyclostrophic balance

is that the poles should generally be colder than the equator; even when

this condition is fulfilled, it is possible that there could be regions where

cyclostrophic balance is not consistent with the temperature field.

At least above the cloud tops, it is easier to monitor the temperature

field of Venus than the wind speeds, using remote sensing techniques. The

implied cyclostrophic wind is in good agreement with direct measurements

of the zonal wind near the cloud tops, but gives an imaginary wind at

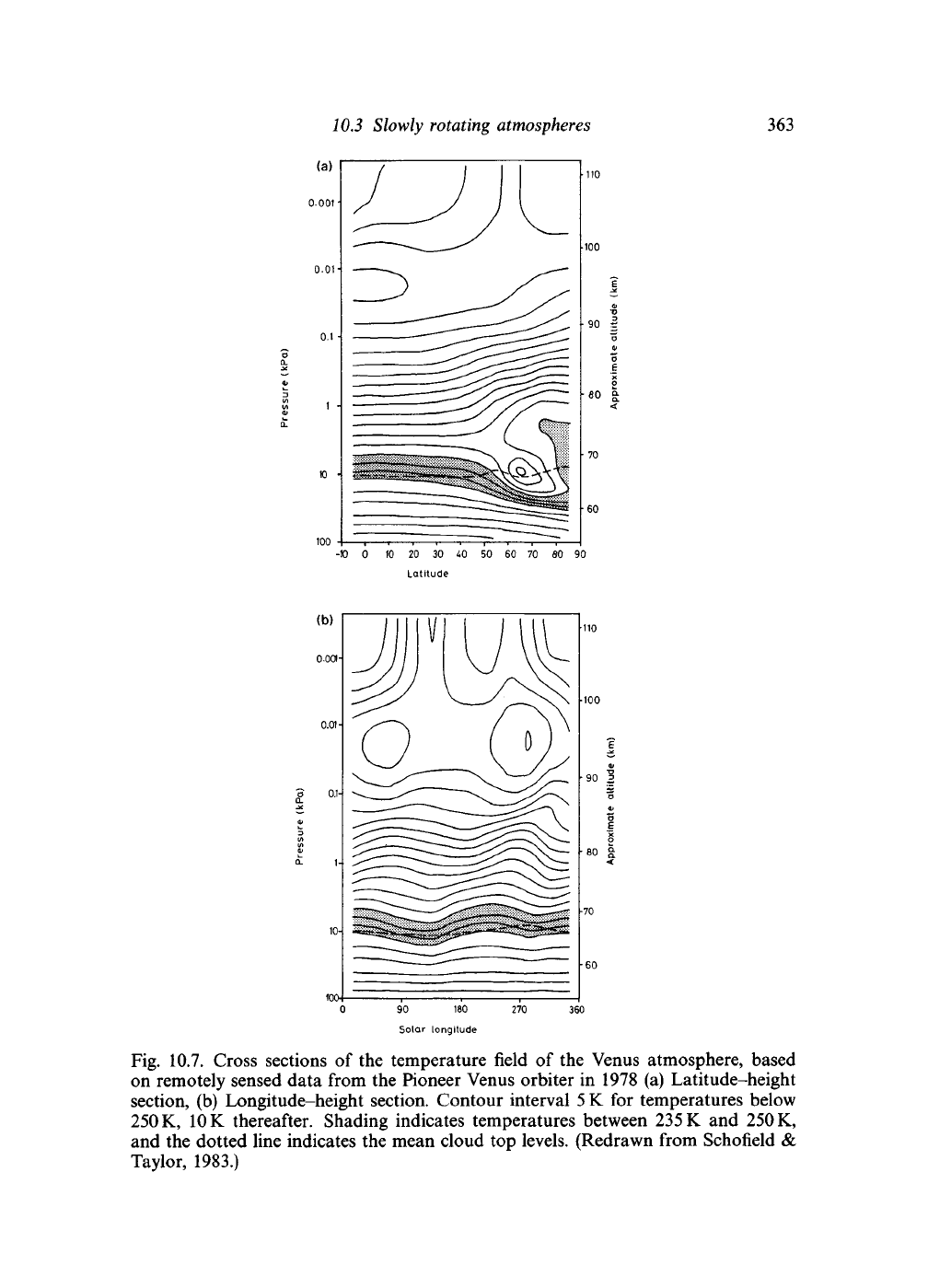
higher levels. Figure 10.7a shows a cross section of the temperature field.

However, the details of the section are a good deal more complex than

simple axisymmetric overturning transporting heat polewards and upwards

would suggest. In particular, there is a minimum temperature around a

circumpolar collar, and higher temperatures over the pole.

The general prograde circulation of the atmosphere of Venus is very dif-

ficult to explain, and certainly cannot be accounted for by axially symmetric

Hadley circulations. The difficulty in obtaining prograde equatorial winds

10.3 Slowly rotating atmospheres

363

0.001

-10 0 10 20 30 40 50 60 70 80 90

Latitude

90 180

Solar longitude

Fig. 10.7. Cross sections of the temperature field of the Venus atmosphere, based

on remotely sensed data from the Pioneer Venus orbiter in 1978 (a) Latitude-height

section, (b) Longitude-height section. Contour interval

K for temperatures below

250

K thereafter. Shading indicates temperatures between

235

K and

250

and the dotted line indicates the mean cloud top levels. (Redrawn from Schofield &

Taylor, 1983.)

364 Planetary atmospheres and other fluid systems

from purely axially symmetric circulations was hinted at in Section 8.3.

Consider such an axially symmetric circulation, in which there may be

friction at the ground, but in which the flow is otherwise inviscid. Such a

flow will conserve the specific angular momentum of air parcels, unless a

torque about the rotation axis acts. The only such torque is provided by

surface friction, and the most this can do is to reduce the air parcel to rest

relative to the solid planet. Thus, the maximum angular momentum which

any air parcel can have is Qa

; conserving this, its zonal wind at any latitude

</>

cannot exceed

sin

</>/

cos

</>

(see Eq. (4.1)). The observed superrotation

indicates that departures from axial symmetry are crucial to the dynamics of

the atmosphere of Venus. Similar arguments must also apply to the strong

equatorial jets observed on Jupiter and Saturn. These must be maintained

by eddies carrying a flux of westerly momentum into the equatorial regions.

The question is: what mechanisms can generate the eddies needed to drive

the Venus superrotation? With such a slow rotation rate, baroclinic instability

may be discounted. Other forms of instability, such as barotropic instability,

might generate Rossby waves which could propagate equatorwards. But

these would have the wrong sign of momentum flux, tending to give a

westerly acceleration to their source latitudes, and an easterly acceleration

to the tropics. Vertically propagating waves, especially trapped equatorial

waves of the kind discussed in Section 7.1, can give a westerly acceleration

to upper levels, as we saw in our discussions of the QBO (Section 8.3). We

still have to explain how such waves can be excited, and we still have to

estimate how strong a prograde acceleration they are capable of imparting

to the atmosphere.

One important candidate for the forcing of

waves

is the thermal tide raised

by the contrast between the heating of the sunlit side of the planet and the

cooling of the night side. According to Table 10.2, the radiative timescale is

very much longer than the rotation period, and so the thermal tide would be

very small. However, this long radiative timescale was based on the mass of

the entire atmosphere, with its huge thermal inertia. Most of the incoming

solar radiation is absorbed near the cloud top levels where the pressure is

around

kPa.

The radiative timescale at these levels is a great deal shorter

than at the surface, and an appreciable thermal tide could be raised. Tidal

theory suggests that the largest response will be in the zonal wavenumber 2

tide.

It is possible for this tidal forcing to excite planetary scale waves which

will propagate vertically away from the source levels. Figure 10.7(b) shows

a longitude height section based on remotely sensed temperature data from

the Pioneer Venus spacecraft. The wavenumber 2 thermal tide is very clear

10.3 Slowly rotating atmospheres 365

near the cloud tops. The phase tilt indicates that the tide is forcing westerly

acceleration near the cloud top levels.

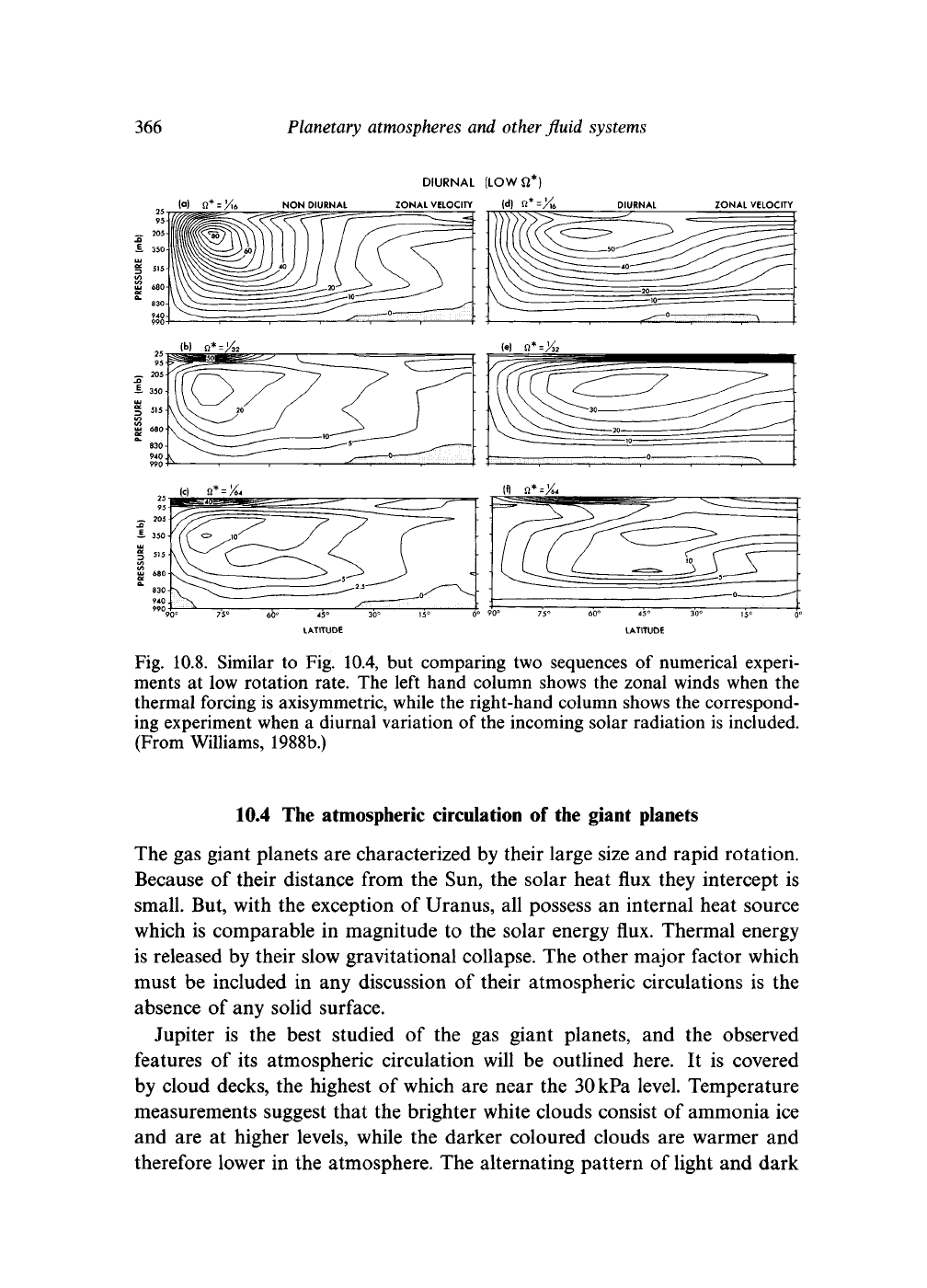
The role of thermal tides in modifying the zonal flow is illustrated by

Fig. 10.8. This is a second sequence of integrations of a terrestrial global

circulation model with different rotation rates due to G.R Williams, similar

to the sequence in Fig. 10.4. On the left are shown [u] for a sequence

of low rotation rate calculations in which the radiative heating is zonally

symmetric. The jet is strongest for a rotation rate l/64th that of the Earth,

where the strongest winds are at

°N.

When a realistic diurnal variation

of the incoming solar radiation is introduced, the westerly momentum is

transported to lower latitudes, and, indeed, westerlies are seen at upper

levels on the equator. Although these experiments reveal that a thermal

tide can drive a superrotation, it is much less strong than that observed on

Venus.

So while the thermal tide hypothesis is plausible, it is still quantitatively

inadequate. Indeed, no theoretical model capable of predicting the observed

strength of the Venus superrotation has yet been proposed. The most suc-

cessful models tend to involve a number of crucial but arbitrary parameters

in the form of anisotropic 'eddy viscosities' or other parameters. Most of

these models can support a prograde flow, but fail to achieve velocities

as large as those observed. So, while thermal tides are very likely to be

involved in generating the superrotation, other effects almost certainly play

an important role. Further progress awaits a more detailed monitoring of

the circulation of Venus for a longer period than the Pioneer probe was able

to achieve. For instance, there is some evidence that the zonal winds may

change substantially over long periods; quasi-periodic phenomena analogous

to the QBO in the Earth's tropics may possibly be present.

The atmosphere of Titan is another example of an atmosphere on a slowly

rotating planet. No direct observations of winds have been made, since a

virtually featureless cloud or haze layer fills the atmosphere. But infrared

measurements indicate fairly large horizontal temperature gradients, espe-

cially at upper levels of the atmosphere. Near the surface, the temperature is

nearly uniform, presumably because the extremely long radiative timescale

means that even very weak motions can smooth out any temperature vari-

ations. But above the haze layer, cyclostrophic balance with the observed

temperature fields indicates strong prograde zonal winds. Once again, the

thermal tide provides one obvious mechanism for generating such winds.

Perhaps strong superrotation is a consequence of any thermally driven flow

on a slowly rotating planet; if so, we scarcely understand the relevant

mechanisms.

366

Planetary atmospheres and other fluid systems

(a)

NON DIURNAL

DIURNAL (LOW 12*)

ZONAL VELOCITY (d) Q*^

ZONAL VELOCITY

350-

UJ 680

830

\ y

(e)

fi*=^

:::••::...: "...:• :

!!! :.

'! \ " ''.'. '...

W .V

'..: •' •••;—^

(C)

fl*

= %4

(f) Q*=X4

Fig. 10.8. Similar to Fig. 10.4, but comparing two sequences of numerical experi-

ments at low rotation rate. The left hand column shows the zonal winds when the

thermal forcing is axisymmetric, while the right-hand column shows the correspond-

ing experiment when a diurnal variation of the incoming solar radiation is included.

(From Williams, 1988b.)

10.4 The atmospheric circulation of the giant planets

The gas giant planets are characterized by their large size and rapid rotation.

Because of their distance from the Sun, the solar heat flux they intercept is

small. But, with the exception of Uranus, all possess an internal heat source

which is comparable in magnitude to the solar energy flux. Thermal energy

is released by their slow gravitational collapse. The other major factor which

must be included in any discussion of their atmospheric circulations is the

absence of any solid surface.

Jupiter is the best studied of the gas giant planets, and the observed

features of its atmospheric circulation will be outlined here. It is covered

by cloud decks, the highest of which are near the

kPa level. Temperature

measurements suggest that the brighter white clouds consist of ammonia ice

and are at higher levels, while the darker coloured clouds are warmer and

therefore lower in the atmosphere. The alternating pattern of light and dark

10.4 The atmospheric circulation of the giant planets 367

cloud bands suggests a sequence of meridional cells, with ascending motion

dominating at the latitudes of the light bands and descent dominating at the

latitudes of the darker bands. Earth based telescopic observations show that

the major features of these bands are long lived, although the individual

bands are interrupted by transient spots and eddies.

Tracking of individual cloud features leads to estimates of the winds at

the cloud top levels, although the interpretation of these measurements is

complicated by the difficulty of assigning an accurate pressure to them. The

winds are referred to a frame of reference rotating with the radio period

of the planet, assumed to reflect the rotation rate of the deep interior.

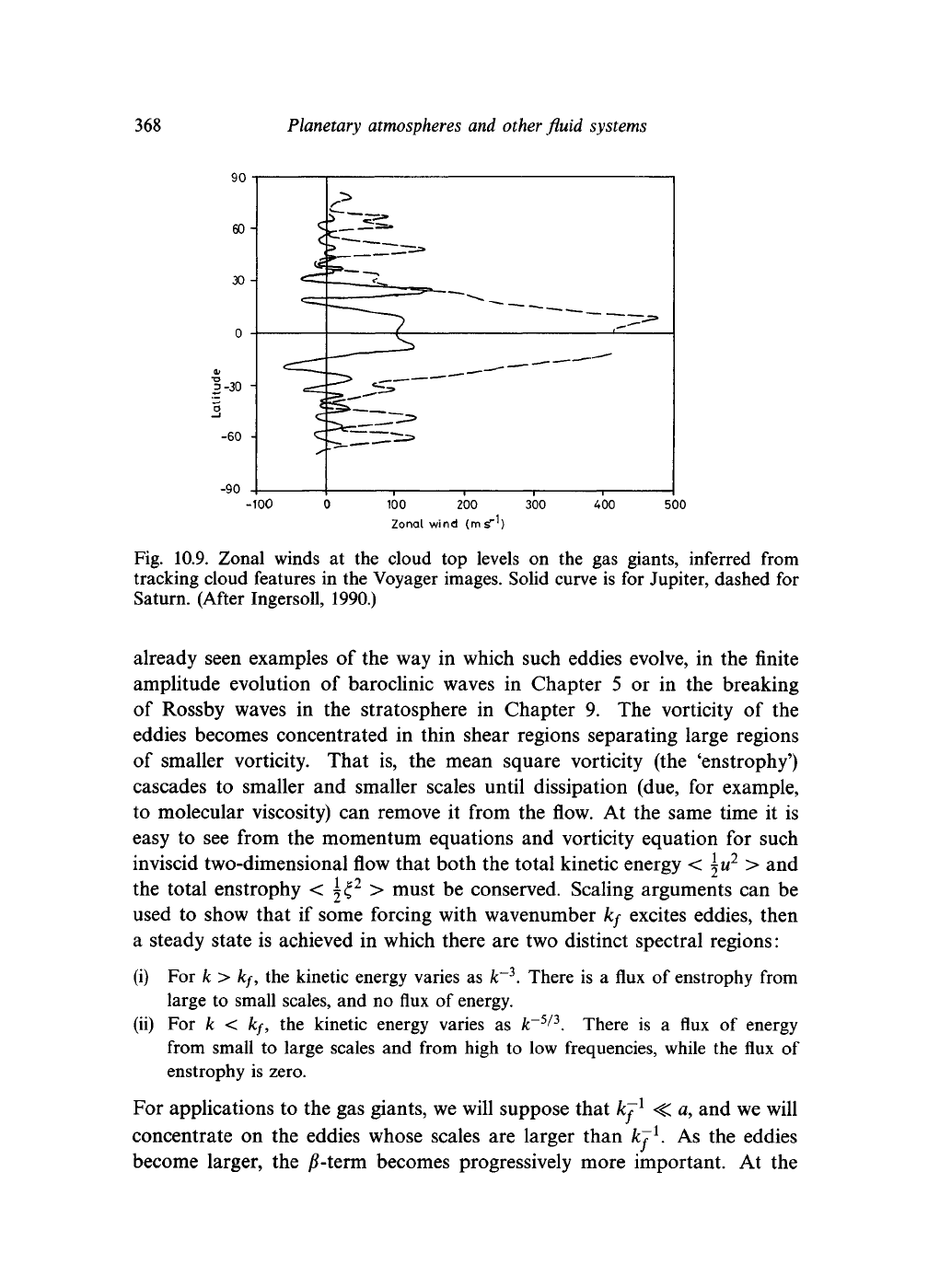
Figure 10.9 shows the pattern of zonal winds observed. A broad region of

strong westerlies, around

100

ms"

blows around the tropics, roughly within

10° of latitude of the equator. At higher latitudes, alternating easterly and

westerly jets are seen. The westerly jets tend to coincide with the higher

cloud layers and the easterly jets with the lower, warmer layers. The bright

elliptical spots which are a prominent feature of the images, some of them

very long lived, all exhibit anticyclonic circulations. Some dark cyclonic

spots,

highly elongated in the zonal direction, were observed around

°N

by Voyager.

Similar observations exist for Saturn and Neptune. Uranus is a special

case which will be discussed separately. The zonal jets on Saturn are stronger

than on Jupiter, with the equatorial jet being broader and with a maximum

wind speed of some

400

ms"

Although more difficult to observe because

of the lack of contrast at the cloud tops, similar features by way of a banded

cloud deck and anticyclonic spots are also characteristic of Saturn.

The presence of equatorial jets on the gas giants is a pointer to the import-

ance of eddies in maintaining the observed circulation. Purely axisymmetric

motions can merely redistribute angular momentum in the meridional plane

and so cannot produce any maxima where the specific angular momentum

exceeds Qa

. Eddies, sheared and distorted by the ambient flow, can provide

the necessary up gradient fluxes of angular momentum to drive equatorial

jets.

They can also drive jets at other latitudes. One group of theories of the

circulation of the major planets would suggest that the observed circulation

is essentially driven by small scale eddies. These are illustrated in their purest

form by the concepts of two-dimensional turbulence on a /?-plane. Rapid

rotation of a barotropic fluid serves to suppress vertical motions and leads

to an essentially two-dimensional flow field.

Consider a random set of strong eddies in a layer of rapidly rotating

fluid. We will suppose that the domain is such that boundary fluxes are

either zero or periodic, and for the moment we ignore the /?-effect. We have

368

Planetary atmospheres and other fluid systems

-90

-100

400

500

Zonal wind (m s )

Fig. 10.9. Zonal winds at the cloud top levels on the gas giants, inferred from

tracking cloud features in the Voyager images. Solid curve is for Jupiter, dashed for

Saturn. (After Ingersoll, 1990.)

already seen examples of the way in which such eddies evolve, in the finite

amplitude evolution of baroclinic waves in Chapter 5 or in the breaking

of Rossby waves in the stratosphere in Chapter 9. The vorticity of the

eddies becomes concentrated in thin shear regions separating large regions

of smaller vorticity. That is, the mean square vorticity (the 'enstrophy')

cascades to smaller and smaller scales until dissipation (due, for example,

to molecular viscosity) can remove it from the flow. At the same time it is

easy to see from the momentum equations and vorticity equation for such

inviscid two-dimensional flow that both the total kinetic energy <\u

> and

the total enstrophy < \t;

> must be conserved. Scaling arguments can be

used to show that if some forcing with wavenumber kf excites eddies, then

a steady state is achieved in which there are two distinct spectral regions:

(i)

(ii)

For k > kf, the kinetic energy varies as k

. There is a flux of enstrophy from

large to small scales, and no flux of energy.

For k < kf, the kinetic energy varies as

fc~

5/3

There is a flux of energy

from small to large scales and from high to low frequencies, while the flux of

enstrophy is zero.

For applications to the gas giants, we will suppose that kj

<a, and we will

concentrate on the eddies whose scales are larger than kj

. As the eddies

become larger, the /J-term becomes progressively more important. At the