James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

5.3

Atmospheric energetics

129

-30S

LATITUDE

Fig.

5.10.

Cross section

the vertical temperature

flux,

[co'T'],

for the DJF

season.

Contour interval 0.02KPas"

, downward (positive) fluxes

shaded.

Based

on six

years

ECMWF

analyses.

simply by integrating over the entire atmosphere. Using pressure as a vertical

coordinate, we have

+ v

= -

—o—dpdxdy,

J Jo 2

where fdp/g represents an integration with respect to mass; the domain A

is taken to be the entire surface of the globe, or least some fraction of that

area so extensive that there is no advection of air into or out of

it.

The result

of such an integration is generally awkwardly large, so it is conventional to

divide X by the area of the Earth's surface Ana

, giving a mean energy per

unit area of the Earth's surface. We will use the notation:

(5.19)

Q being any meteorological quantity, as a convenient shorthand. Having

defined the global kinetic energy, consider how it might be altered. Consistent

with the quasi-geostrophic approximation, the momentum equation may be

written:

d\ d\ v

—

+ v

•

Vv + (o— + /k x v = -V<t> (5.20)

at dp

(see Eqs. (1.65a) and (1.65b)). Note that the horizontal advection term can

130

Transient disturbances

in the

midlatitudes

be rewritten

V(v

•

v/2)

VK, where

K is the

local kinetic energy

per

unit

mass

of the

atmosphere.

The

last term

is an

idealization

real frictional

processes,

in the

form

of a

Rayleigh drag. Take

the

scalar product

this

equation with

the

horizontal components

the wind:

+ v

K + a^ =

-v.Va>-— (5.21)

which

is an

energy equation

for the

flow. Note that

the

Coriolis force

can

work, since

acts perpendicularly

to the

velocity.

The

last term states

that

the

kinetic energy

dissipated

twice

the

rate

of the

momentum.

are

left

deal with

the

vertical advection

kinetic energy,

and the

horizontal advection

the geopotential. Consider

the

latter. After using

the

continuity equation,

<9<t>

•

V<D

•

(<Dv)

^-(co<D)

co—. (5.22)

But

d<S>/dp

to the

potential temperature through

the

hydrostatic

relation,

Eq.

(1.68):

-Hp)d.

(5.23)

Hence, writing the advection terms

flux form, and incorporating Eqs. (5.22)

and (5.23)

the

kinetic energy equation becomes:

+ V

•

(\(K +

<D))

^-(co(K

0>))

-hcoO

- —.

(5.24)

Now integrate the kinetic energy equation over the globe

give

expression

for

the

rate

change

global kinetic energy.

By the

divergence theorem,

the integral with respect

area

the second term

can be

written:

•

(\(K +

<D))

= I \(K +

<D)

•

(5.25)

where

denotes

the

horizontal area

of the

atmosphere

and L

denotes

the

circuit around the edge

the domain. But this

zero, since there

supposed

be no

inflow

outflow across

the

boundaries

(or,

more elegantly

for a

spherical world,

it is

zero because

v and (K +

O) satisfy periodic boundary

conditions). Similarly,

the

vertical boundary conditions

are

= 0 at p = p

and

p = 0, so

that

the

vertical integral

of the

third term

zero.

after

some algebraic labour,

the

final expression

for the

rate

change

global

kinetic energy

found

to be

rather straightforward:

±(K) = (-hcoe)-(2K/T

(5.26)

5.3 Atmospheric energetics 131

But this is simply the statement made in Chapter 3 on thermodynamic

grounds; kinetic energy is generated if there is a net correlation between

ascent and positive temperature anomalies, and vice versa. That is, there

must be a preponderance of thermally direct circulations. This generation of

kinetic energy may be offset by the frictional dissipation of kinetic energy.

In order to generate this kinetic energy, we must have depleted some

potential energy. But the potential energy of the atmosphere is not a very

useful concept. It would be minimized by compressing all the air into an

infinitely thin layer near the ground. But such a compression is physically

unrealistic. It would require enormous amounts of work to be done against

pressure forces, and this work would go to increase the internal energy, that

is,

the temperature, of the air. Only if this internal energy could be radiated

steadily away to space would the potential energy be reduced, and it would

have gone, not into kinetic energy, but into thermal radiation. In other

words, most of the potential energy associated with the mass distribution

in the atmosphere is unavailable for conversion into kinetic energy. That

part of the energy which is available for conversion, the 'available potential

energy', is a small fraction of the total. The available potential energy is

defined as that part of the potential energy which can be released without

any change of the internal energy of the atmosphere. From the first law of

thermodynamics, and remembering that the total mass of the atmosphere

does not change, it must be released by adiabatic mixing of air parcels.

Formally, the available potential energy is defined as the maximum amount

of potential energy which could be destroyed by adiabatic mixing of the

atmosphere. Figure 5.11 illustrates the concept. Whether such mixing is in

fact possible depends upon the dynamic constraints to which the system is

subject. In Fig. 5.11

(a),

the isentropes are not parallel to the geopotentials.

We may imagine adiabatic processes which could exchange the wedge of

potentially warmer air marked A for the wedge of potentially colder air

marked B. The result would be to replace the mass of air B with somewhat

less dense air from A, while the air mass A would be replaced by denser air

from

The mean mass distribution would have been lowered slightly and so

a certain amount of potential energy would have been destroyed. Once the

isentropes are parallel to the geopotentials, no further adiabatic exchanges

of air masses with different potential temperatures are possible. Accordingly,

the potential energy released in going from the state shown in Fig. 5.11 (a)

to the state in Fig. 5.11(b) is indeed the 'available potential energy'.

These arguments are restricted to the usual situation of a statically stable

atmosphere, in which the static stability is not supposed to vary on pressure

surfaces. This is a consistency requirement for a quasi-geostrophic descrip-

132

Transient disturbances

the midlatitudes

(a)

geopotential

isentrope

geopotential

Fig. 5.11. Illustrating the concept of available potential energy.

tion of

the

dynamics. More elaborate definitions of available potential energy

which overcome these restrictions have been proposed, and are mentioned

in the bibliography.

We may now proceed, with

the

benefit

of a

degree

hindsight,

to a

more formal mathematical definition

available potential energy

in the

quasi-geostrophic framework. The thermodynamic equation can be written:

(5.27)

form which is consistent with the quasi-geostrophic approximation. The

potential temperature anomaly 9

is defined as

= 0-0

(p)

(5.28)

where 9

the reference atmosphere, consisting

the global mean

9 at

each level. Note that since 9

does not vary

time

or in

the horizontal,

5.3 Atmospheric energetics

133

Differential

heating

Available

potential

energy

Upward

heat fluxes

Kinetic

energy

Friction

Fig. 5.12. The generation, conversion and dissipation of energy in the global circu-

lation.

^,0

+V- v

can be replaced by 6

Eq. (5.27). Take the product

this equation with

, giving:

(5.29)

and integrate over the globe.

As in

the discussion

the kinetic energy

equation, the global integral

the second term

zero

virtue

the

boundary conditions, and so we have:

(5.30)

The first term on the right hand side is equal in magnitude but opposite in sign

to the kinetic energy generation term in Eq. (5.26). Therefore, (h

/2s

)

the quantity depleted as kinetic energy is generated; accordingly,

must be

an expression for the available potential energy A.

is seen that A depends

essentially

on the

temperature variance

on a

given geopotential surface,

consistent with

the

schematic picture given

Fig. 5.11. Equation (5.30)

states that available potential energy

depleted

by net

thermally direct

circulations,

which upward motion

correlated with warm temperature

anomalies. Available potential energy is generated in circumstances in which

the heating accentuates warm anomalies and cools cold anomalies.

Putting Eqs. (5.26) and (5.30) together, an idealized picture of the global

circulation emerges, shown in Fig. 5.12. Differential heating creates available

potential energy, which

converted

kinetic energy

thermally

dir-

ect circulations. Friction balances the energy budget by dissipating kinetic

energy. As

stands, this description adds very little to the results obtained

in Chapter

on general thermodynamic grounds.

more useful form

energetics is obtained when the kinetic and available potential energies are

split into their zonal and eddy parts.

Consider, first, the zonal part of the available potential energy. The zonal

134

Transient disturbances

the

midlatitudes

mean

the thermodynamic equation

is:

[0],

\v\[0]

jtt-

WF]

+ [I],

(5.31)

where the subscript notation

used

denote partial differentiation and

the

eddy terms have been

put on to the

right hand side.

For

brevity,

the

eddy

fluxes have been written

in a

form which includes both

the

transient

and

steady eddy contributions, since,

to a

good approximation:

[

*9*]

[v*e

] +

[v'O'l

(5.32)

The zonal available potential energy, denoted

AZ, is

obtained

multi-

plying

Eq.

(5.31)

[9]/s

and

integrating over

the

entire globe.

The

multiplication yields:

The second term

on the

left hand side integrates

zero,

arguments

similar

those used above which make

use of

the boundary conditions

[v].

The global average

the second term

on the

right

can be

rewritten

the more convenient form:

(^^e"]

-(K[e]ybfW]\.

(5.34)

This identity

easily established

integrating

parts with respect

to y

and using the conditions that

= 0 at

the edges

the domain (or, equally,

that

the

boundary conditions

on all

variables

are

cyclic

in y).

Finally, from

Eq. (5.33) we can show that:

(h[6][co])

/^[0M^]\

+ O^Wffl)

•

(5.35)

With

the

exception

of the

second term,

all the

terms

are

very straight-

forwardly related to the zonal mean version of the various terms in Eq. (5.30).

This second term

is a

new effect;

represents

the

conversion

zonal into

eddy available potential energy

by the

action

of an

eddy component

meridional wind

in the

presence

of a

basic poleward temperature gradient.

The difference between Eqs. (5.35)

and

(5.30) yields

expression

for the

rate

change

the eddy available potential energy, AE, where

[¥

36)

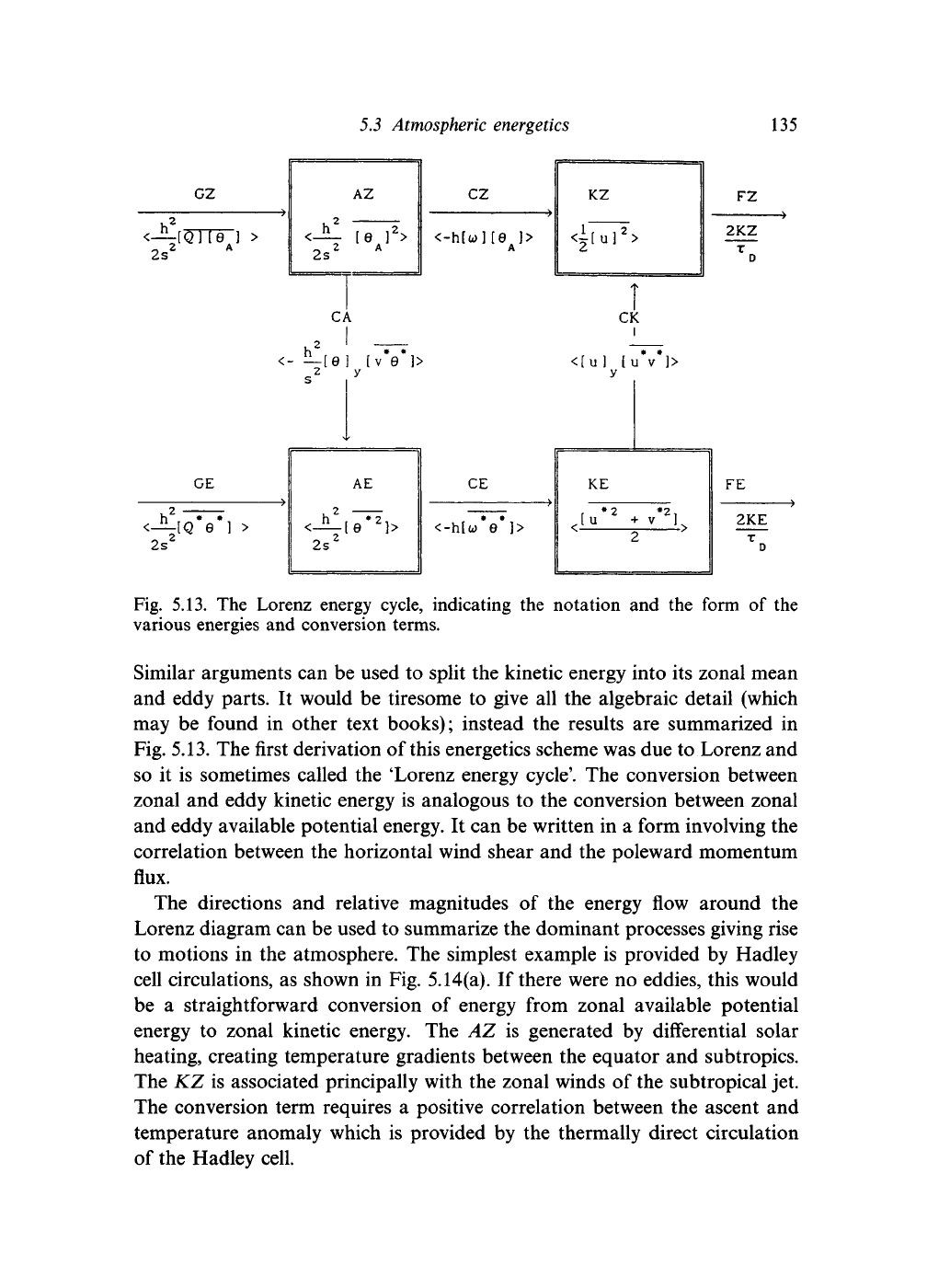
5.3 Atmospheric energetics

135

<—[Q] [e ] >

]

<-h[u>]

2KZ

Fig. 5.13. The Lorenz energy cycle, indicating the notation and the form of the

various energies and conversion terms.

Similar arguments can be used to split the kinetic energy into its zonal mean

and eddy parts. It would be tiresome to give all the algebraic detail (which

may be found in other text books); instead the results are summarized in

Fig. 5.13. The first derivation of this energetics scheme was due to Lorenz and

so it is sometimes called the 'Lorenz energy cycle'. The conversion between

zonal and eddy kinetic energy is analogous to the conversion between zonal

and eddy available potential energy. It can be written in a form involving the

correlation between the horizontal wind shear and the poleward momentum

flux.

The directions and relative magnitudes of the energy flow around the

Lorenz diagram can be used to summarize the dominant processes giving rise

to motions in the atmosphere. The simplest example is provided by Hadley

cell circulations, as shown in Fig. 5.14(a). If there were no eddies, this would

be a straightforward conversion of energy from zonal available potential

energy to zonal kinetic energy. The AZ is generated by differential solar

heating, creating temperature gradients between the equator and subtropics.

The KZ is associated principally with the zonal winds of the subtropical jet.

The conversion term requires a positive correlation between the ascent and

temperature anomaly which is provided by the thermally direct circulation

of the Hadley cell.

136 Transient disturbances in the midlatitudes

During the 1930s and 1940s, there was considerable debate about the

origin of eddy motions in the atmosphere. One possibility was that the

strong shears associated with the poleward edge of the subtropical jet would

prove hydrodynamically unstable. Such 'barotropic instability' would result

in conversion of KZ to KE and would require that the momentum fluxes

would be negatively correlated with the wind shears. In terms of the eddy

structures, we would see eddies tilting against the background wind shear.

Fig. 5.14(b) illustrates the Lorenz energy diagram associated with this view

of the global circulation.

The second possibility, which rapidly became the accepted mechanism

following the work of Charney and Eady in the latter part of the 1940s, was

that 'baroclinic instability' generated the eddies. The energetics of baroclinic

instability are illustrated in Fig. 5.14(c); temperature fluxes correlated with

a poleward temperature gradient convert AZ to AE. Upward heat fluxes

then convert AE to KE. Baroclinic instability theory, which will be outlined

in Section 5.4, indicates the conditions under which such a pattern of

conversions is dynamically consistent.

Figure 5.15 gives observed values of the various energies and conversions,

estimated from observed data. The vertical velocities were inferred from

the horizontal wind and mass fields during initialization prior to carrying

out a numerical forecast integration (see Section 2.2). It will be seen that

the dominant conversions are those associated with baroclinic instability,

although only quite a small fraction of AZ is actually converted into other

forms of energy. The conversion between AZ and KZ is small and its sign

is somewhat uncertain. This arises from the near cancellation between a

negative contribution to

(/*[#]

[co])

from the Hadley cell and the positive con-

tribution from the thermally indirect Ferrel circulations of the midlatitudes.

There is no trace of barotropic instability, the conversion CK having the

wrong sign for this. Rather, the momentum fluxes are associated with the

transient eddies returning kinetic energy to the zonal flow and so helping to

maintain the tropospheric jets in midlatitudes.

An analysis of

the

energetics of

the

global circulation is helpful in revealing

the dominant pattern of energy conversions in the atmosphere. If care is

taken, these may be regarded as the signatures of basic physical processes

occurring, such as baroclinic instability. But the usefulness of the energetics

approach is limited in a number of respects.

First, it must be appreciated that the kinetic energies and available poten-

tial energies cannot vary independently in the midlatitudes. For instance, in

Section 5.2, we found that the poleward thermal advection of a developing

baroclinic wave is inevitably accompanied by an upward temperature flux.

5.3 Atmospheric energetics

137

! AE i

(a)

I KE i

: AZ

]

! AE !

(b)

(c)

(d)

Fig. 5.14. Paradigms of the Lorenz energy cycle, (a) Axisymmetric Hadley circula-

tions (b) barotropic instability, (c) baroclinic instability, (d) observed global

circulation.

36.9

11.5

(

4.7

2.0

)

0.33

7.5

1.7

)

Fig. 5.15. Lorenz energy cycle as observed for the December-February period. Units:

Jm"

(energies) and Wm"

(conversions).

This is necessary to maintain thermal wind balance. Similarly, the generation

of AZ associated with the forcing of an equator-pole temperature contrast

must lead, by thermal wind balance, to the generation of westerly wind shear

in midlatitudes, and hence to an associated KZ. The KZ generated by eddy

momentum fluxes, on the other hand, is barotropic in structure and so need

138 Transient disturbances in the midlatitudes

not be accompanied by any change of AZ. It is perhaps preferable to reject

the distinction between eddy available potential and kinetic energy, defining

instead a single 'eddy energy':

)

(5.37)

Eddy energy is created by the negative correlation between the temperature

flux and the temperature gradient, and is destroyed if there is a positive cor-

relation between momentum flux and horizontal wind shear. But, of course,

this is only a diagnostic relationship. In order to decide whether baroclin-

ically unstable waves can form on any particular zonal flow, it is necessary

to show that energy releasing disturbances, with the necessary phase tilts

and other structures, can be maintained in a dynamically consistent fashion

in that flow. Our discussion in the next section will address these issues.

Second, the analysis is a truly global diagnostic. It is very difficult to

construct an energetics scheme for a limited area. The boundary fluxes

rapidly become the dominant terms. But the global budget is likely to

include a number of processes with quite different signatures in different

regions. An example was given above, where it was shown that the Hadley

and Ferrel cells make large contributions to the AZ to KZ conversion which

nearly cancel. The net AZ to KZ conversion is therefore a small residual

between large effects of opposite sign arising from the Hadley cell in the

tropics and the Ferrel cell in the midlatitudes. The magnitude and even the

sign of this conversion are very uncertain.

5.4 Theories of baroclinic instability

The energetics discussed in the last chapter revealed that, because of the

horizontal temperature gradients in a stably stratified atmosphere, potential

energy is available in principle for conversion into eddy energy. The eddy

fluxes required for the necessary conversions of energy also define the sort of

structures that must characterize such growing eddies. But these considera-

tions alone do not guarantee that growing eddies can in fact be sustained. The

demands of thermal wind balance restrict the scale and shape of dynamically

possible eddies. In this section, we will outline a more predictive approach

which will define the conditions under which unstable eddies can be expected,

and which will determine their scale and rate of growth.

The philosophy behind these theories is to imagine small perturbations

growing on a zonally uniform basic state. It is found that certain classes