James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

5.4

Theories ofbaroclinic instability

139

of disturbance can grow, and it is presumed that the most rapidly growing

disturbances will come to dominate the observed flow field. The mathematics

is common to a large class of hydrodynamic instability problems, and will

not be discussed very deeply. The reader is referred to books such as that

by Pedlosky (1987) for a full mathematical discussion. The basic principle

is to linearize the governing equations around the zonal mean state by neg-

lecting the products of eddy quantities. A 'normal mode' solution to the

linearized equations is then sought, leading to a relationship defining the

time behaviour of the various normal modes permitted.

A number of idealized mathematical models of the baroclinic instability

problem have been derived. Perhaps the simplest and most elegant is that due

to Eady; accordingly we will discuss this extensively. Other calculations give

rather similar results, though often at the expense of a considerable increase

in algebraic complexity. The basic state envisaged in the Eady model is

illustrated in Fig. 5.16. It proves convenient to formulate the problem using

'pseudo-height' (or the logarithm of pressure) as vertical coordinate:

-H]n(p/p

)

(5.38)

where H is the atmospheric pressure scale height and p

is the reference

atmospheric pressure in the system. Boundaries are located at z' = +H/2.

The lower boundary represents the Earth's surface; the upper boundary can

be interpreted as a representation of the tropopause, which behaves roughly

as a rigid lid on the tropospheric motions. The Eady problem neglects the

variation of the Coriolis parameter / with latitude; solutions will be sought

which are periodic in both the x- and y-directions. Baroclinic instability

is made possible in the system by a uniform temperature gradient in the

y-direction which does not vary with height. Equivalently, by thermal wind

balance, the zonal wind increases linearly with height; the vertical wind shear

is denoted AU/H. The description of the system is completed by specifying

a stratification, measured by the Brunt-Vaisala frequency N where

In principle, N

may vary with z', but for simplicity we will restrict our

attention to the case where

is a constant.

The evolution of the system can be described using the quasi-geostrophic

equations of Sections 1.7 and 1.8, but expressed in log-pressure coordinates.

These may be succinctly summarized by conservation of potential vorticity:

^q = 0,

(5.40)

140

Transient disturbances in the midlatitudes

AU/2

-H/2

Fig. 5.16. Schematic diagram of the configuration envisaged for the Eady model of

baroclinic instability.

provided friction and heating can be ignored. The potential vorticity of the

undisturbed zonal flow is given by

— J

xp d

' dy

where the streamfunction

is defined by

xp = -AUyz'.

(5.41)

(5.42)

Substituting into Eq. (5.41), it is quickly seen that the potential vorticity of

the basic state is constant and equal to /. Since Eq. (5.40) states that this

potential vorticity cannot be altered by the subsequent development of the

flow, it follows that the perturbation potential vorticity q* remains zero for

all time:

ay ay f ay

(5.43)

* dx

' dy

' N

dz'

This relationship serves to determine the structure of any wavelike perturba-

tions.

We assume that the initial eddy is periodic in x, y and t (this involves

no loss of generality, since any arbitrary disturbance could be resolved into

a Fourier series of periodic disturbances), and has the form:

ip*

(5.44)

where <J>(z') is a function of height to be determined. Then, since the potential

vorticity perturbation is zero for all time, it follows that:

where K

= k

. The solutions to this ordinary differential equation in z

are most conveniently written as:

= A cosh(z'/H

) + B sinh(z'/H

), (5.46)

5.4

Theories ofbaroclinic instability

141

where

the

constants

integration

A and B are yet to be

determined.

The

first term

this solution

symmetric about

the

midlevel

= 0,

while

the

second

antisymmetric.

Equation (5.46) determines

the

spatial structure

of the

eddies,

but

says

nothing about their time variations.

determine these,

must apply

the

boundary conditions

at z'

—

+H/2. The

boundary conditions

are

simply

= 0 at

each boundary. However,

does

not

occur

in the

potential

vorticity

Eq.

(5.40).

complete

the

problem,

will

use the

perturbation

thermodynamic equation

relate

the

vertical velocity

to the

eddy potential

temperature

and

hence

to the

eddy streamfunction.

The

usual linearization,

whereby

all

products

eddy quantities

are

dropped, will

assumed.

Making use

the hydrostatic relation

relate temperature and geostrophic

streamfunction,

the

quasi-geostrophic thermodynamic equation

is:

~H~^)

vs7)"

•

47)

Thus setting w

0, we have

Substituting

for

xp*

using

Eq.

(5.46) gives

the

relationships between

the

frequency

the disturbance

and its

spatial structure:

{±As +

Bc)

-f~

{Ac

±Bs) = 0 at z

= ±H/2

where

c = cosh(KNH/2f), s = sinh(KNH/2f).

(5.49)

These

two

relationships

can be

used either

eliminate

the

unknown

con-

stants

A and 5, or to

eliminate

the

unknown frequency co.

In the

first case,

a 'dispersion relation' linking

the

frequency

to the

wavenumbers

the eddy

results:

= i

where

f/(NH).

In the

second case,

the

ratio

B/A is

obtained, thereby

completing

the

description

the vertical structure

the modes:

2 ^t

nh(K/2K

)-K

/K)

l±coth(K/2K

)-K

/K)'

Consider, first,

the

frequency given

by Eq.

(5.50).

For

small

K, the

142 Transient disturbances

in the

midlatitudes

expression for co

is negative, indicating that the frequency is imaginary.

That is, the time variation is either exponential growth or exponential decay,

depending on which sign of the square root is taken. In a physical system,

the exponentially growing modes will quickly dominate. In this case, the

fluid is hydrodynamically unstable, and we will show that the mode of in-

stability is indeed the baroclinic instability whose energetics were described

in the last section. For K > 2399 K

, co is real, and we have neutrally

stable,

propagating disturbances. The most unstable modes are for / = 0 and

k =

l.61K

when the growth rate a is given by

a =

ico

= 031K

AU =

031-1—AU.

(5.52)

N H

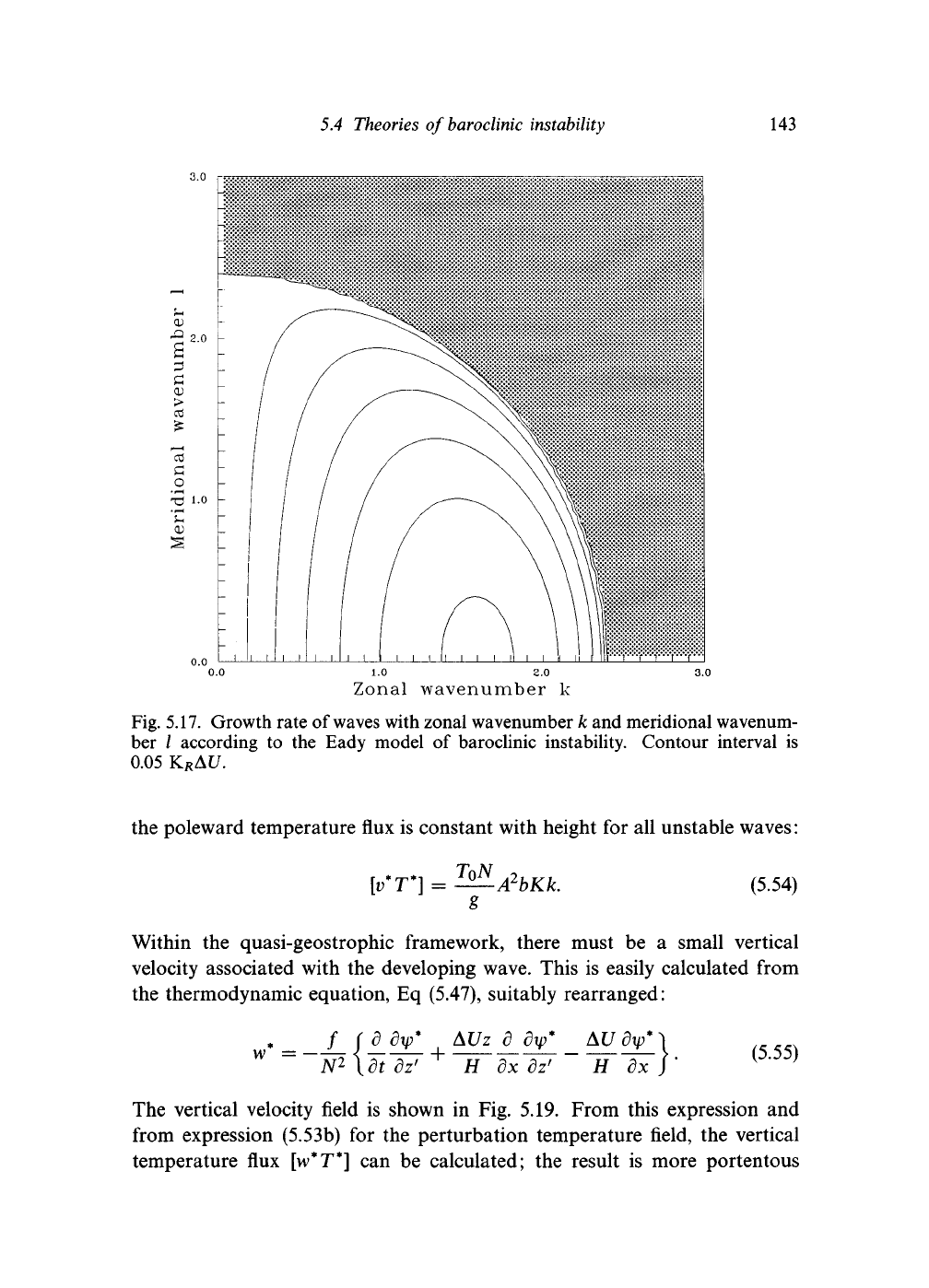
Figure 5.17 shows the variation of growth rate with both k and /. Taking

typical values of / and N for the midlatitude troposphere, we find that the

wavelength of the most unstable mode is around 4000 km, and the growth

rate is about 0.5 day"

. This is very similar to the scales for high frequency

transients which were deduced in Section 5.2.

Equation (5.51) shows that the ratio (B/A)

is negative for the unstable

waves,

that is, (B/A) is imaginary. This implies a vertical phase tilt, and,

consequently, a nonzero poleward temperature flux. The stable waves, with

K >

2.399K

have no phase tilt and zero temperature flux. We concentrate

on the unstable modes. Denote b = i(B/A). From the perturbation stream-

function, it is straightforward to deduce the eddy poleward velocity and the

eddy temperature fields, which are:

v* = kA

coth f —-— J sin kx

—

sinh f —-— j cos kx

(5.53a)

r_MMJ

sinh

(EE£)

siakx

bcosb

(a**)cos**).

(5.53b)

I \ f J \ f J

Figure 5.18 shows plots of these fields as a function of x and z

. The poleward

velocity shows a characteristic westward phase tilt with height, amounting

to 90° for the most unstable wave. A similar phase tilt is found for the

streamfunction perturbation. The temperature perturbation, on the other

hand, has an eastward phase tilt with height of

48 °

between the bottom and

top boundaries. The temperature and poleward velocity waves are exactly

in phase at the midlevel. Towards the boundaries, the phase difference is

larger, but the amplitudes also increase. In fact, using the mathematics of

Section 5.2, it is easy to show that these effects exactly compensate, so that

5.4 Theories

baroclinic instability

143

1.0

2.0

Zonal wavenumber k

Fig. 5.17. Growth rate of waves with zonal wavenumber k and meridional wavenum-

ber

according

to the

Eady model

baroclinic instability. Contour interval

0.05 K

AU.

the poleward temperature flux is constant with height for all unstable waves:

(5.54)

Within

the

quasi-geostrophic framework, there must

be a

small vertical

velocity associated with the developing wave. This is easily calculated from

the thermodynamic equation, Eq (5.47), suitably rearranged:

H dxdz>

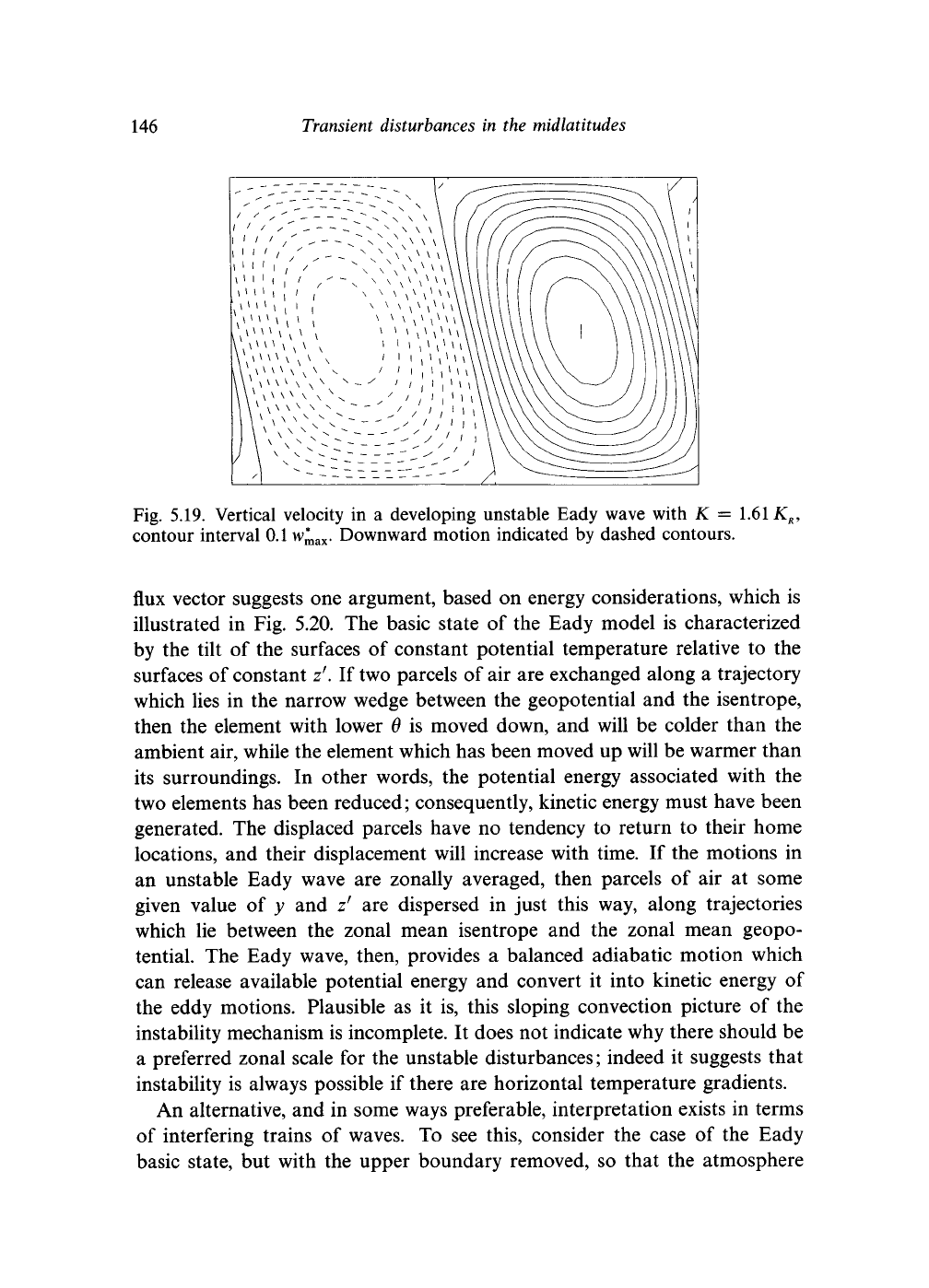
The vertical velocity field

shown

Fig. 5.19. From this expression and

from expression (5.53b) for the perturbation temperature field, the vertical

temperature flux [w*T*] can

calculated; the result

more portentous

144

Transient disturbances

in the

midlatitudes

than enlightening, but is quoted for the sake of completeness:

T ] =

< Si sinh

( — ) +

cosh

[ -— +

sinh

—

)},

Ng { \HJ \Hj \H

(5.56)

where

c _

c -

and

AUk

By comparing [w*T*] and [t>*T*], it can be seen that the growing Eady

wave has a temperature flux which is directed at an angle typically midway

between the geopotentials and the surfaces of constant potential temperature

(or density). This feature is characteristic of the baroclinic instability process,

which is why it is sometimes called 'sloping convection'. It is also character-

istic of the observed midlatitude transients and, as we showed in Section

3.3,

such an upward and poleward temperature flux is required on general

thermodynamic grounds. A plot of w* for the most unstable Eady wave is

shown in Fig. 5.19. A comparison of this field with the temperature anomaly

shown in Fig. 5.18(b) reveals that upward motion tends to be correlated

with warm temperatures, and downward motion with cold temperatures.

Consequently, the baroclinically unstable Eady wave transports heat upwards

as well as polewards.

In terms of the energetics of the preceding section, the horizontal eddy

temperature flux is constant and poleward, while the poleward temperature

gradient is constant through the y-z

plane in the Eady model. There is a

continual conversion of zonal available potential energy into eddy available

potential energy, in just the way suggested for baroclinic instability. The

associated vertical temperature fluxes are required to maintain thermal wind

balance in the developing wave, and they ensure that there is conversion of

eddy available potential energy to eddy kinetic energy. The existence of the

same energy conversions in observations of the global circulation strongly

suggests that baroclinic instability is indeed the source of the transient

eddy activity observed in the midlatitudes. The fact that the Eady theory

predicts the wavelength and growth time of unstable disturbances to be

close to those observed for the midlatitude transients is further evidence that

baroclinic instability is dominating this aspect of the global circulation.

A number of alternative physical interpretations of the nature of the baro-

clinic instability process can be given. The sloping nature of the temperature

5.4 Theories ofbaroclinic instability

145

1 1

Fig. 5.18. Structure of the meridional velocity perturbations (left) and the tempera-

ture perturbations (right) in growing Eady waves. The contour interval is 0.1 t^ax

or 0.1 T^

, as appropriate. Negative values indicated by dashed contours, (a)

K = 0.1 K

. (b) K = 1.61 K

(the most unstable wave), (c) K = 2.3 K

near the

short wave

cutoff.

146

Transient disturbances in the midlatitudes

Fig. 5.19. Vertical velocity in a developing unstable Eady wave with X = 1.61 K

contour interval 0.1 w^

. Downward motion indicated by dashed contours.

flux vector suggests one argument, based on energy considerations, which is

illustrated in Fig. 5.20. The basic state of the Eady model is characterized

by the tilt of the surfaces of constant potential temperature relative to the

surfaces of constant z'. If two parcels of air are exchanged along a trajectory

which lies in the narrow wedge between the geopotential and the isentrope,

then the element with lower 6 is moved down, and will be colder than the

ambient air, while the element which has been moved up will be warmer than

its surroundings. In other words, the potential energy associated with the

two elements has been reduced; consequently, kinetic energy must have been

generated. The displaced parcels have no tendency to return to their home

locations, and their displacement will increase with time. If the motions in

an unstable Eady wave are zonally averaged, then parcels of air at some

given value of y and z' are dispersed in just this way, along trajectories

which lie between the zonal mean isentrope and the zonal mean geopo-

tential. The Eady wave, then, provides a balanced adiabatic motion which

can release available potential energy and convert it into kinetic energy of

the eddy motions. Plausible as it is, this sloping convection picture of the

instability mechanism is incomplete. It does not indicate why there should be

a preferred zonal scale for the unstable disturbances; indeed it suggests that

instability is always possible if there are horizontal temperature gradients.

An alternative, and in some ways preferable, interpretation exists in terms

of interfering trains of waves. To see this, consider the case of the Eady

basic state, but with the upper boundary removed, so that the atmosphere

5.4 Theories of baroclinic instability

147

Fig. 5.20. Schematic illustration of the 'sloping convection' explanation of the Eady

instability. Parcel A has lower potential temperature than parcel B. Consequently,

exchanging them reduces the potential energy of the system.

extends to z

= +oo. We take the lower boundary to be at z

= 0. From

Eq. (5.45), the form of the disturbances is:

xp*

= Azxp{—z'/H

} exp{i(foc + ly

—

cot)}

(5.57)

since we require that they die away as z

—>

oo. As previously, the thermo-

dynamic equation is used to express the lower boundary condition w = 0 in

terms of

and hence to determine the dispersion relationship for wavelike

disturbances. From this, it is found that the frequency

is always real, so

that instability is not possible. The phase speed co/k is:

fAU 1

(5.58)

indicating that the wave moves at the same speed as the fluid a distance

from the boundary. Exactly the same arguments would apply to a rigid

boundary at the top of an infinitely deep atmosphere. The structure of such a

neutral mode is shown in Fig. 5.21. The neutral modes for the Eady problem

beyond the short wave

cutoff,

when K > K

, tend towards just this structure;

they become so shallow that we have essentially independent trains of waves

trapped on the upper and lower boundaries. For longer wavelengths, the

upper and lower waves in the Eady problem become deeper until they have

significant amplitude at the opposite boundary. At this point, they will begin

148

Transient disturbances in the midlatitudes

(b)

Fig. 5.21. (a) The perturbation streamfunction for a neutral Eady wave trapped

on the lower boundary of an infinitely deep atmosphere, (b) Schematic diagram

showing how phase locking between two such waves can lead to instability.

to interact with each other. Now suppose that the phase speeds of the upper

and lower waves are such that they do not move relative to one another.

The circulations induced by the lower wave can induce further meridional

displacements in the upper wave, and vice versa, provided the upper trough

is to the west of the lower trough. When such phase locking is possible, the

waves will be growing, unstable disturbances.

Two other analytical models of baroclinic instability have been used extens-

ively for theoretical studies. They will be outlined much more briefly than

the Eady model. The first is the 'two-layer' model. Figure 5.22 illustrates the

configuration of this model. The vertical structure of the flow is represented

by defining the streamfunction on just two levels in the vertical; the various