Jackson Mark. Machining with Abrasives

Подождите немного. Документ загружается.

importance, but its shape and surface structure were for the tool-workpiece inter-

actions. Its surfaces were formed by preferred diamond/fcc cleavage planes and

were used as rake and clearance faces. The edge radius was not chosen to be

atomically sharp (2 nm) in order to consider limited mi nimum edge radii because

of surface stresses. To further provide a reasonable tool-workpie ce contact model,

the tool structure had the atomic density of diamond. Although the tool was

modeled as a hard body with collectively moving atoms, i.e., no interaction within

the tool, the interaction potential between tool and workpiece atoms needed to be

speciﬁed. Data for the diamond/copper interactions based on a pair potential

function were found. The cutting forces were calculated as reaction forces at the

tool due to its feed motion. The work atom interactions are described by the EAM

potential for copper. Th e cutting speed was restricted to 100 and 50 m/s. Lower

speeds were not practical to simulate due to computational limitations.

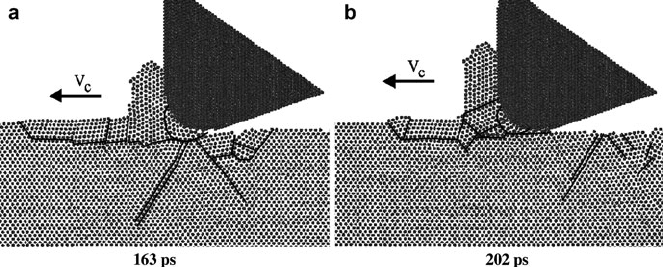
Figure 7.1 shows a single-crystalline structure, that moved relative towards the

cutting tool, whereupon material is deformed in front of the tool tip, the chip

generation is initiated and dislocation loops can be identiﬁed at the generated

workpiece surface. It shows areas of plastic deformation, dislocations and large

elastic deformations in the sub-surface region. The method is based on horizontal

and vertical connections between initial-neighbor atoms. Deformations show as

sharp equilateral folds in neighboring layer lines within the otherwise rectangular

structure or by narrowing mesh spacing as in case of strong elastic deformation. For

large displacements between initial-neighbor atoms, the bond was considered to be

broken and was not drawn anymore. In this way, highly deformed areas, like the

chip and the newly generated surface, show few initial-neighbor lines. Deep

running dislocations, observed in 2D MD cutting simulations if pair potentials are

being used, could not be conﬁrmed by employing this 3D model and the better

EAM potential. This model predicts intensive plastic deformation at the generated

surface with a thickness of only a few atom layers. At the same strain, a 2D model

Fig. 7.1 Deformation graph, view <110> (after Rentsch in Davim and Jackson [1]). Used with

permission copyright ISTE-Wiley (2009)

7 Nanogrinding 305

always predicts larger dislocations than its 3D counterpart. The cutting process

changes drastically when changing the ratio of depth of cut to cutting edge radius

from 0.5 to 1.0, depending also on the crystalline orientation of the work. At a ratio

of a/r ¼1.0, the tool begins to utilize more its rake face for the chip formation. With

the increase in depth of cut, the portion of twin dislocations in chip formation

increases over dislocation slipping.

Such twinned areas can be seen ahead of the tool and the chip. The lower energy

requirement for twinning makes the chip removal process at larger depth of cut

more efﬁcient and the cutting forces only increase under proportionally. Figure 7.2

shows two subsequent 2D views of microstructural snapshots of the same model as

in Fig. 7.1, but at smaller depths of cut than before. Analyzing the changes in the

microstructure deepens the understanding of the mechanisms of material removal

for speciﬁc cutting conditions. In Fig. 7.2 areas with different crystal orientation are

separated by lines and slip lines drawn for identiﬁed dislocations. Until state (a) was

reached, the pre-deformation area in cutting direction (ahead of the chip) increased

without an increase in chip length. Until state (b) was reached, this process had

stopped, the pre-deformation area decreased while the chip grew in size. The micro

structural plots show a change of the crystal orientation in the chip root area, that

supports either the deformation away from the chip root (a) or the chip formation in

the chip root area.

7.3 Cutting Forces, Stress and Temperature

By modeling systems of discrete particles and observing their progression over

time, statistical mechanics provides a basis for the analysis and the description of

the behavior of such systems. It has been demonstrated for a Gibbs micro canonical

Fig. 7.2 Micro structural changes in the chip root area during chip formation (after Rentsch in

Davim and Jackson [1]). Used with permission copyright ISTE-Wiley (2009)

306 M.J. Jackson and J. P. Davim

ensemble, that taking time averages is in statistical agreement with taking phase-

space averages and, that the numerical quality of results in MD can always be

improved by longer calculations.

Cutting forces can be calculated as reaction forces at the tool due to its relative

motion during contact with the workpiece atoms. For every time step Dt, which is

usually in the range of a few femtoseconds (10

15

s), the force contributions of the

workpiece atoms interacting with the tool are integrated. The dynamic character of

such a system with a large number of degrees of freedom, i.e., all the freely moving

workpiece atoms, emerge as ﬂuctuations of derived, non-constant quantities.

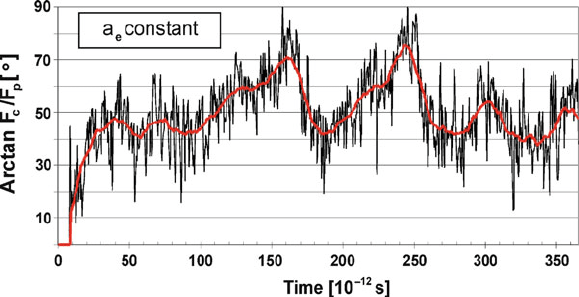
Figure 7.3 shows the course of the cutting force ratio for the simulation in Fig. 7.2.

The instantaneous tool forces, which will be newly calculated for every time step,

ﬂuctuate intensively. Calculating a moving average of the force ratio over, e.g., 1,000

time steps cancels out the ﬂuctuations and leads to a smooth course. After over-

coming the equilibration phase (no cutting forces), the ﬁrst tool/workpiece contact

was made and the force ratio changed to an average value of 1 (¼arctan 45



)overa

period of about 20 ps (10

12

s). Besides smaller maxima and minima during the

observed total process simulation time, two gradually developing maxima in the

course of the force ratio appear at about 165 and 245 ps. Figure 7.3 sheds light on the

micro structural process that is related to the observed course of the force ratio.

Detailed information about the distribution of stresses and temperature in nano-

scale cutting are of high interest for science and manufacturing industry. So far

most of the MD results of cutting process simulations were presented as atomic,

discontinuous sets of instantaneous data at individual atom sites, such as snap shot

atomic positions, relative displacement and instantaneous atomic temperature.

Besides the limited meaning of instantaneous atomic temperatures and stresses,

looking at such large sets of 10,000, 100,000 or even millions of data is not practical

from a point of view of efﬁcient data analysis. Furthermore, it makes any attempt to

compare MD results with, for instance, results from continuous mechanics difﬁcult

Fig. 7.3 Course of the cutting force ratio Fc/Fp (after Rentsch in Davim and Jackson [1]). Used

with permission copyright ISTE-Wiley (2009)

7 Nanogrinding 307

if not impossible. Taking advantage of the possibility of improving the quality of

local values by calculating them as time averages over sufﬁciently long period of

time provides the means to obtain a deeper insight of the model and the simulated

process. Thus, aiming at macroscopic thermodynamic properties, suitable time

intervals for averaging these properties have to be identiﬁed. Simulations showed

that an average over about 1,000 time steps led in some cases to sufﬁciently stable

mean prope rties, but still provide a certain time resolution in order to study details

of the process. Considering the basics of MD and the physical nature of these

quantities, the results can now be represented in form of gradual distributions as so-

called contour plots, with a certain resolution in space as well as in time. The

representation of stresses and temperature in terms of continuous distributions

allows a direct comparison of continuous mechanics results and MD results.

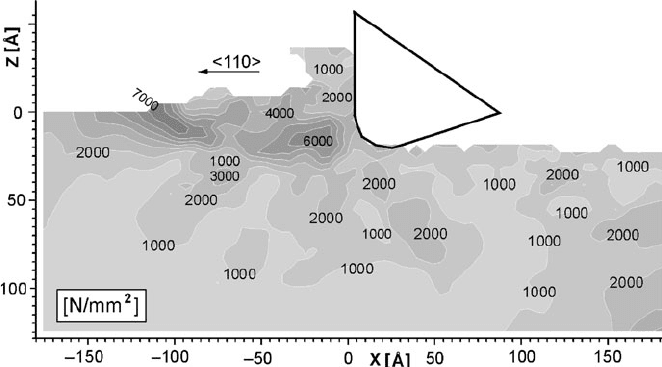
In Fig. 7.4 the calculated distribution of the maximum shear stress of the

orthogonal cutting process already shown in Figs. 7.1 and 7.2 is given. With the

help of this distribution it is possible to determine where stress concentrations

occur, how much the crystal structure inﬂuences the stress distribution, as well as

the material removal process, and what the differences are in comparison to

macroscopic, continuou s mechanics processes.

This also allows the determination of how the process inﬂuences the motion of

the workpiece and where new dislocations can occur, since areas of high shear

stress are potential sources for formation or extension of dislocations. Similarly also

temperature distributions can be calculated by adopting [7] to local volumes and

calculating time averages. As it will be shown in the following chapter, MD cutting

process simulations without the consideration of ﬂuids lead to approximately

concentric temperature distributions, in which the hottest area is the chip area and

Fig. 7.4 Shear stress distribution in an orthogonal 3D MD machining model (after Rentsch in

Davim and Jackson [1]). Used with permission copyright ISTE-Wiley (2009)

308 M.J. Jackson and J. P. Davim

the chip root area. At the tip of the tool, the material is deformed at a high stress

level, whereby a lot heat it generated. Hence, the high temperature areas extend

from the chip under the tip of the tool, as one important source of heat generation,

to the areas of shearing. It should be noted here, that modeling the tool by rigid,

thermally not active atoms, does not enable the tool to conduct any heat. Therefore

the tool acts like a thermal isolator, which further supports a concentration of heat

in the chip.

Regarding the temperature distributions in MD cutting it should be further noted,

that in most of the published work only the thermal conductivity through phonons is

considered. The conductivity by electrons is neglected in such case, even though it

is one order of magnitude larger than that of the phonons. Hence, the presented

temperature levels as well as the local gradients would actually be lower than

shown. New algorithms were developed to describe thermal conductivity more

accurate by considering both, the electron and the phonon conductivity.

7.4 Three-Dimensional Machining Simulations

Two aspects of advances and recent developments in material removal process

simulation using MD will be explained in some more detail, which are the possi-

bility of carrying out complete 3D surface machining simulations and the consider-

ation of ﬂuids. For abrasive processes the model requirements are higher than for

cutting processes, since orthogonal symmetry is not give n and a quasi-2D model,

cannot be applied. Besides the need to describe the geom etry of abrasives, the

model has to provide sufﬁcient space for the deformation and chip formation of the

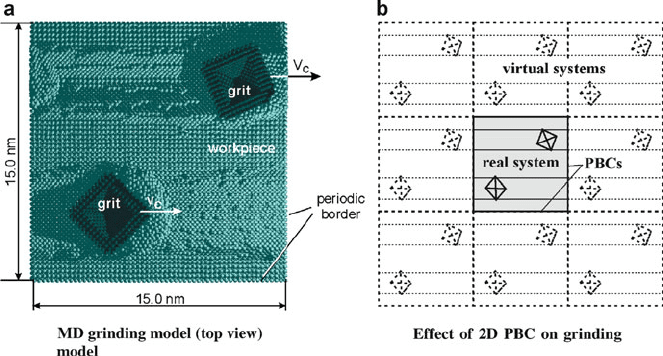
three-dimensional material removal process. Figure 7.5a shows a snapshot of a

molecular dynamics simulation to study material pile-up and chip formation in

abrasive machining as a function of shape and orientation of the abrasives.

The simulation in Fig. 7.5 considered two pyramidal grains with diamond

structure and two different orientations. The ﬁgure shows an advanced state of

the 3D grinding simulation using a model with more than 100,000 copper atoms

(the workpiece height was 6 nm). In several terms the simulation represents a high-

end state-of-the-art MD simulation of the grain/workpiece contact as the interac-

tions were based on an EAM potential function and the model considers two

abrasives that cut at 100 m/s through a workpiece over its whole length. Hence,

the periodic boundaries (for both directions of the horizontal plane) lead to com-

plete groove formation by the grits in a cutting direction and describe a model setup

with multiple grit/workpiece contacts that occurs in nanogrinding. By repeating the

complete groove generation with relative-to-the-cutting-direction shifted abrasives,

the machining of the whole surface can be realized. This provides the basis for 3D

surface roughness and residual stress analyses of completely machined surfaces at

realistic machining speeds (common grinding speeds range from about 5 to 80 m/s

and high speed grinding up to about 250 m/s).

7 Nanogrinding 309

Thorough the analyses of the chip formation, the elastic and plastic response of

the workpiece and process quantities in MD simulations have revealed clear and

consistent effects. For example, the machining speed has a direct inﬂuence on the

microscopic material removal process and the chip formation in MD simulations.

The resu lts suggest, that the sensitivity of the simulation results on the machining

speed is less strong than observed in experimental investigations. A possible reason

for this effect is, that the implemented boundary conditions and model settings have

a strong impact on the dynamics of the ﬁnite process model. However, signiﬁcant

changes in magnitude of the machining speed lead to signiﬁcant changes in chip

shape and formation mechanism. Further quantities of the process are affected due

to an increasing localization of the deformation process at high speeds. More direct

effects on the process simulation results show the depth of cut, the grit orientation

and the cutting edge radius. Hence, it is possible with MD to simulate the inﬂuence

of grain shape and orientation on the efﬁciency of abrasive processes. On basis of

bigger MD models, it will be possible to determine the energy dissipation by a

direct analysis of elastic and plastic work and the microscopic mechani sms that

determine the surface roughness in nanoscale machining processes.

7.5 Experimental Nanogrinding

The piezoelectric nanogrinding process is a process that relies on using a nickel-

coated ceramic material with microscale diamond particles bonded to it that are

cubo-octahedral in shape to machine nanoscale features in a variety of workpiece

Fig. 7.5 Snapshot of a full model length scratching simulation with two hard abrasives (after

360,000 time steps, 144 ps) (after Rentsch in Davim and Jackson [1]). Used with permission

310 M.J. Jackson and J. P. Davim

materials. The diamonds are bonded to the piezoelectric material by gaseous

deposition, laser cladding, or directly bonding a porous tool to the material via an

adhesive paste. The process is executed by applying a known sinusoidal frequency

to the piezoelectric crystal in order to achieve a desired oscillatory displacement.

Rapid vibration of the crystal will allow material removal rates to be increased, thus

making it a nanomanufacturing process. The nanogrinding process is accompanied

by wear of the diamond grains, and the rate of this wear plays an important role in

determining the efﬁciency of the nanogrinding process and the quality of the

nanomachined surface. Wear mechanisms in nanogrinding processes appear to be

similar to that of single-point cutting tools, the only difference being the size of

swarf particles generated. Figure 7.6 show s the arrangement of grinding swarf and

abrasive grains that have been lost during the nanogrinding process.

Figure 7.6 shows abrasive grains with blunted cutting edges (wear ﬂats), and

abrasive grains with sharp cutting edges that are released from the surface of the

piezoelectric crystal before they have chance to grind nanoscale chips from the

surface of the workpiece. The process suffers with a loss of diamond grains even

when the interfacial adhesion between diamond and piezoelectric material is very

good. A more closely related process that has been reported widely is that of the

wear of probes used in atomic force microscopy [2, 3]. However, these observations

were purely experimental with no explanation of how to design probes that inhibit,

or retard, wear. A performance index used to characterize diamond wear resistance

is the grinding ratio, or G-ratio, and is expressed as the ratio of the change in volume

of the workpiece removed, Dv

, to the change in the volume of the diamond

abrasive grain removed, Dv

, and is shown in (7.1),

Fig. 7.6 Nanoscale grinding detritus showing blunt and sharp abrasive grains of diamond and

7 Nanogrinding 311

G ¼ Dv

(7.1)

Grinding ratios for processes at the nanoscale have not yet been characterized.

However, the complexities of wear of abrasive materials at any scale lead us to

believe that the variety of different and interacting wear mechanisms involved,

namely, plastic ﬂow of abrasive, crumbling of the abrasive, chemical wear etc.,

makes the wear of diamond at the nanoscale too complicated to be explained using

a single theoretical model [4]. The following analysis of diamond grains repre-

sented by loaded wedges assumes that grain fracture is the dominant wear mecha-

nism when grinding at the nanoscale using the piezoelectric nanogrinding process.

7.5.1 Analysis of Nanogrinding Grains

Diamond grains are blocky in nature and possess sharp cutting points prior to

nanogrinding workpiece materials. Figure 7.7 shows a collection of diamond

abrasive grains that have well deﬁned cutting points that form a wedge at their

apex. When bonded into a strong matrix, these grains can be considered to be

representative inﬁnite wedges.

An inﬁnite wedge represents the cutting point of an abrasive grain in contact

with the workpiece material (Fig. 7.8).

Fig. 7.7 A collection of diamond grains showing cutting points located at their apex, and

locations of {100} and {110} planes. Diamond grains are approximately 60 mm in diameter.

312 M.J. Jackson and J. P. Davim

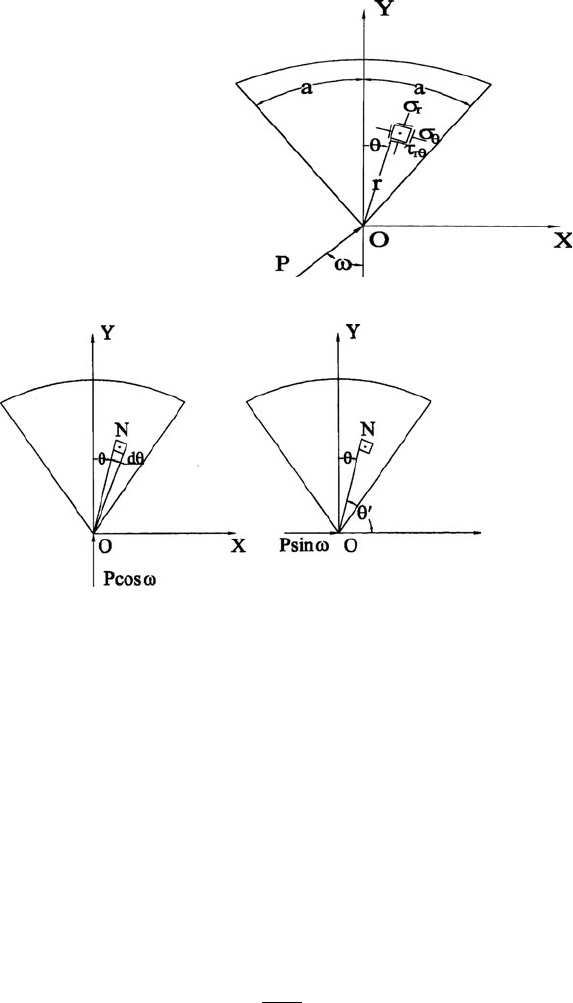
The wedge is loaded at the apex by a load P in an arbitrary direction at angle o to

the axis of symmetry of the wedge. Resolving the force into components Pcos o in

the direction of the axis, and Psin o perpendicular to that the stresses due to each of

these forces can be evaluated from two-dimensional elastic theory [5]. The state of

stress in the wedge, due to force Pcos o, can be obtained from the stress function,

’ ¼ C  r  y sin y (7.2)

where r and y are polar coordinates, or the point N in Fig. 7.9, and C is a constant.

The stress function yields the following radial, tangential, and shear stress

components,

¼2C

cos y

(7.3)

Fig. 7.8 The single-point,

loaded inﬁnite wedge. Used

with permission copyright

Springer (2007)

Fig. 7.9 The single-point, loaded inﬁnite wedge showing force components, and the point N

within the wedge at polar co-ordinates, r and y. Used with permission copyright Springer (2007)

7 Nanogrinding 313

¼ 0 (7.4)

¼ 0 (7.5)

To determine the constant, C, the equilibrium of forces along the y-axis is:

P cos o 

a

 cos ydA ¼ 0 (7.6)

where dA is an element of cross sectional area within the wedge. If, t, is the

thickness of wedge, then,

cos oP ¼

a

cos y

 t  r  cos ydy ¼ 2Ct

a

cos

ydy

¼ Ct 2a þ sin 2a½ (7.7)

Therefore,

C ¼

P cos o

tð2a þ sin 2aÞ

(7.8)

And,

¼

2P cos y  cos o

r  tð2a þ sin 2 aÞ

(7.9)

Note that the negative sign denotes that the stress is compressive. The state of stress

in the wedge, due to force Psin o, can be obtained from the stress function,

’ ¼ C

 r  y

 sin y

(7.10)

Therefore,

¼2C

cos y

(7.11)

¼ 0 (7.12)

¼ 0 (7.13)

Equilibrium of forces along the x-axis (Fig. 7.9) yields the following solution for

the constant, C,

314 M.J. Jackson and J. P. Davim