IX Международная конференция Новые идеи в науках о земле. Доклады

Подождите немного. Документ загружается.

S-XXVIII. Секция численных методов и математического моделирования 201

ВСПЛЕСК-ФРАКТАЛЬНОЕ СЖАТИЕ ИЗОБРАЖЕНИЙ

А.А. Брыксин

ГОУ ВПО МГТУ «СТАНКИН», Москва, Россия

В данной работе автор предлагает метод сжатия изображений, являю-

щийся комбинированием двух алгоритмов – всплеск-сжатия с использованием

нуль-деревьев и фрактального сжатия в области всплесков (фрактально сжи-

мается не само изображение, а его всплеск-преобразование). Комбинирование

происходит следующим образом: для всплеск-сжатия оценивается отношение

степени компрессии к искажениям для разных участков изображения, те уча-

стки, где это отношение мало, сжимаются фрактально.

Всплеск-сжатие с использование нуль-деревьев основывается на двух

важных наблюдениях:

В основном, изображения имеют низкочастотный спектр. Когда изобра-

жение раскладывается по базису всплесков, энергия в частотных полосах

уменьшается с уменьшением масштаба (маленький масштаб означает вы-

сокое разрешение). Таким образом, в среднем, всплеск-коэффициенты

будут меньше в высших частотных полосах, чем в низших.

Большие всплеск-коэффициенты несут больше информации.

Само всплеск-сжатие происходит в два этапа. На первом этапе изображе-

ние подвергается дискретному всплеск-преобразованию, и коэффициенты

представляются в виде дерева, у которого каждая вершина, кроме корня, имеет

четыре потомка. На втором этапе происходит кодирование этого дерева алго-

ритмом, основанном на нуль-деревьях (например, EZT).

Таким образом, изображения, которые имеют плавные переходы цвета,

будут иметь сильную степень компрессии. Те же изображения, которые силь-

но текстурированы, будут сжиматься плохо.

Фрактальное сжатие изображения основывается на предположении о на-

личии самоподобных частей в изображении. Поэтому высокая степень сжатия

достигается на сильно текстурированных изображениях и изображениях,

имеющих обширные монотонные области. Идея фрактального сжатия заклю-

чается в следующем: предположим, что изображение является неподвижной

точкой некоторого сжимающего отображения. Тогда можно вместо самого

изображения запомнить каким-либо образом это отображение, а для восста-

новления изображения достаточно многократно применить это отображение к

любому начальному изображению. По теореме Банаха, такие итерации приво-

дят к неподвижной точке, то есть к исходному изображению. На практике в

качестве сжимающих отображений берутся сжимающие аффинные преобразо-

вания, и сжатое изображение представляется коэффициентами этих преобра-

зований. Фрактальное сжатие в области всплесков имеет дело не с самим изо-

бражением, а с его всплеск-коэффициентами, представленными в виде дерева.

Указанный выше метод комбинирования этих алгоритмов дает лучшую сте-

пень сжатия, чем каждый из них, однако занимает больше времени.

Работа выполнена под руководством д.ф.-м.н., проф. Н.Н. Холщевниковой.

202 S-XXVIII. Секция численных методов и математического моделирования

ОБ УСКОРЕНИИ ИОНИЗОВАННОГО ГАЗА В ПЛОСКОМ КАНАЛЕ

М.Б. Гавриков

, Г.В. Шмаровоз

РГГРУ имени Серго Орджоникидзе, г. Москва, Россия

ИПМ им. М.В.Келдыша РАН, г. Москва, Россия

В работе применительно к течениям в каналах рассмотрена двухжидкостная

гидродинамическая модель, согласно которой плазма – это совокупность двух

взаимопроникающих сжимаемых газов – электронного и ионного, распределен-

ных по всей области течения. Более того, показано, что в нерелятивистском слу-

чае двухжидкостная гидродинамика может быть математически эквивалентным

образом сведена к одножидкостной – уравнениям электромагнитной гидродина-

мики (ЭМГД), которые формально получаются из системы классической МГД

добавлением лишних слагаемых. Именно эти слагаемые оказываются ответст-

венными за многие тонкие эффекты динамики плазмы, недоступные МГД, такие

как, например, мощное ускорение в каналах плазменных ускорителей и пр.

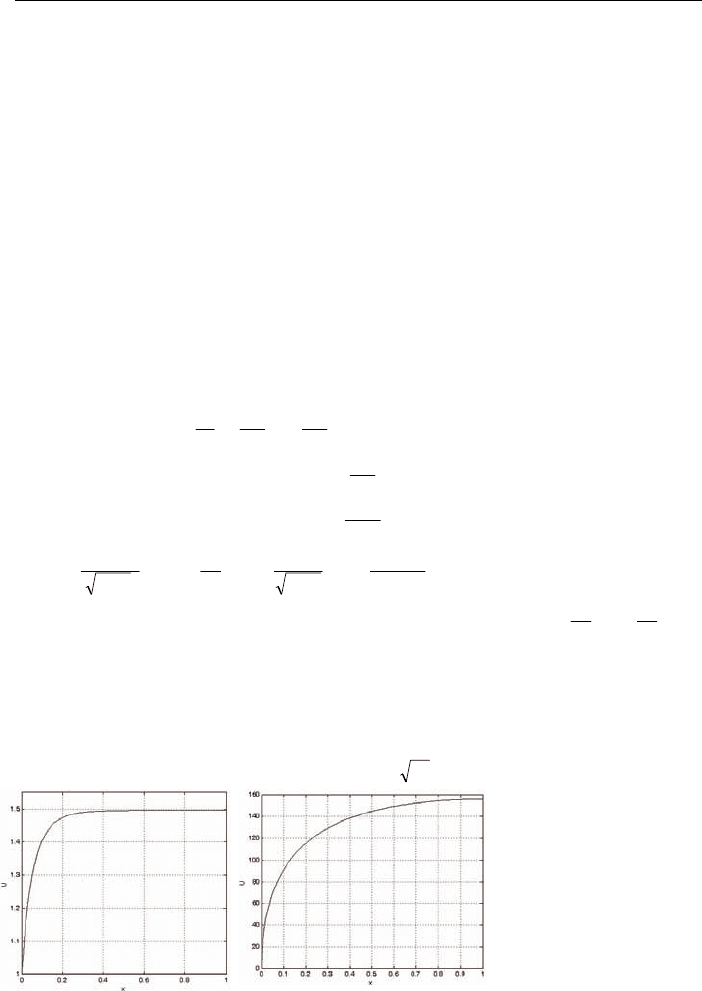
Для плоского канала в приближении холодной плазмы распределение

безразмерной продольной скорости течения плазмы U и напряженности H по-

перечного магнитного поля находятся из уравнения:

10,0

≤≤=+−+

⎟

⎠

⎞

⎜

⎝

⎛

xEUH

μξ

(1)

,0)1(,1)0( ==

(2)

),1(

1)(

HUU

−+==

(3)

где

2/12/1

σπ

πρπρ

λλ

====

а ρ

, U

, H

– параметры плаз-

мы на входе, σ – поперечная проводимость, l–длина канала,

λλ

В работе исследованы квазиодномерные стационарные решения ЭМГД-

системы применительно к установившимся течениям плазмы в канале, к стен-

кам которого подводится напряжение.

Проведенные расчеты выявили новый по сравнению с МГД механизм ус-

корения плазмы в каналах. Его действие локализовано в узком слое шириной

порядка погонного числа частиц порядка

)(

−

, примыкающем ко входу в

канал, а ускорение

может достигать де-

сятков и сотен раз.

На графиках пред-

ставлены зависимости

безразмерной скоро-

сти U от приведенной

длины канала x.

S-XXVIII. Секция численных методов и математического моделирования 203

ВОССТАНОВЛЕНИЕ ПАРАМЕТРОВ

МНОГОМЕРНЫХ САМОПОДОБНЫХ ФУНКЦИЙ

ПРИ ПОМОЩИ ВСПЛЕСК-ПРЕОБРАЗОВАНИЯ

Н.А. Елистратов

ГОУ ВПО МГТУ «Станкин», Москва, Россия

Достаточно широкий класс фракталов, имеющих свойства самоподобия,

можно описать при помощи самоподобных функций. А именно, назовем само-

подобной функцией решение функционального уравнения

∑

−=

iiii

rxMfMpxf

))((det)(

где , – невырожденные квадратные матрицы размера

Rr ∈

, – параметры. Задача численной оценки этих параметров

представляет интерес при идентификации модели экспериментальных данных.

R∈

r ,p

i i

M ,

Для решения одномерной задачи С. Малла и В.Л. Хвонг использовали

свойство самоподобия максимумов модуля всплеск-преобразования. В пред-

ставленной работе рассматривается многомерный аналог всплеск-

преобразования

)(*),( xfxSWf

, где

SxSx

det/)()(

1−

Было показано, что такая свертка сохраняет свойства самоподобия и кривые

маскимумов непрерывны в направлении малых масштабов, если

– функция

Гаусса.

В работе предложен алгоритм с голосованием численной оценки пара-

метров самоподобия, являющийся обобщением одномерного алгоритма.

Большинство фракталов, встречающихся в физике или обработке изображе-

ний, не являются в точности самоподобными. Отклонения от самоподобия

могут быть интерпретированы как ренормализационный шум. Процедуры с

голосованием, такие как преобразование Хафа, особенно успешны при восста-

новлении параметризованных кривых из зашумленных данных. Одним из не-

достатков такого подхода является то, что голосование представляет собой

процедуру полного перебора, что ведет к увеличению сложности при возрас-

тании размерности.

Для иллюстрации предложенного метода приведены результаты расчетов

параметров одномерного множества «рваный отрезок» и двумерного фрактала

«двуглавый дракон».

204 S-XXVIII. Секция численных методов и математического моделирования

СЕГМЕНТАЦИЯ И КЛАСТЕРИЗАЦИЯ

СЕГМЕНТОВ ВРЕМЕННЫХ РЯДОВ

СИСТЕМ МОНИТОРИНГА

А.А. Любушин

ИФЗ РАН и РГГРУ, Москва, Россия

Исследуется проблема автоматической сегментации временных рядов

мониторинга большой длительности и последующего кластерного анализа

облака векторов признаков, полученных от каждого сегмента. Подобного рода

задачи возникают в геофизике, медицине, биологии с целью выявления

скрытой структуры данных и поиска предвестников катастрофических изме-

нений свойств изучаемых объектов (сильных землетрясений в земной коре,

например).

Рассматриваются несколько методов, основанных на выделении стати-

стически значимых резких скачков уровня исследуемых сигналов или их стан-

дартного отклонения с помощью длинных цепей скелетов максимумов модуля

непрерывных вейвлет-преобразований, а также на исследовании локальных

максимумов меры нестационарности временных рядов при ее оценке в двой-

ном скользящем временном окне с использованием разности между матрица-

ми Фишера авторегрессионной модели, оцененной слева и справа от централь-

ной точки скользящего окна.

Для последующего кластерного анализа выделенных сегментов исполь-

зуется вектор признаков, состоящий из значений параметров мультифракталь-

ных спектров сингулярности сигналов внутри выделенных сегментов, а также

коэффициентов авторегрессионной модели и логарифма остаточной диспер-

сии. Исследуются вариации различных статистик, характеризующих степень

кластеризации облака векторов признаков сегментов в так называемом собы-

тийном окне, то есть временном окне переменной длительности, содержащем

одинаковое число векторов.

Методы иллюстрируются примерами анализа данных низкочастотного

микросейсмического фона и электроэнцефалограмм.

S-XXVIII. Секция численных методов и математического моделирования 205

ОБ АЛГОРИТМАХ ПОСТРОЕНИЯ ОРТОГОНАЛЬНЫХ ВЕЙВЛЕТОВ

А.Ю. Максимов

РГГРУ имени Серго Орджоникидзе, Москва, Россия

Если финитная масштабирующая функция

φ генерирует p-адический

кратномасштабный анализ в L

(⁭

), то она удовлетворяет уравнению

() (

pa p

−

∑

α),

(1)

где Ө − операция p-ичного вычитания на

⁭

. Если a

= a

= ··· = a

p-1

и все

= 0 для

≥

, то решением уравнения (1) является характеристическая

функция промежутка

)

−

⎡

⎣

(в частности, при n = 1 получается функция

Хаара

[

)

). При

решения уравнения (1) с коэффициентами

(

)

1/aab=++ 4

(

)

1/b=+− 4aa

(

)

1/aab=−− 4

(

)

1/aab=−+ 4

где

1ab+=

, изучались Лэнгом [1]. Эти решения являются фрактальными

функциями с носителями на отрезке

[0,2] и представимы в виде

2-1

( ) (1/2)(1 ( /2))

xabw

∞

∑

, (2)

[

)

0, 2 ,x∈

где

(x) – классические функции Уолша на ⁭

. В общем случае разложения

решений уравнения (1) в лакунарные ряды по обобщенным функциям Уолша

были найдены Ю.А. Фарковым. Эти разложения имеют вид

[

)

0,1

(,)

()(1/)(/)(1 (/)

lpn

xp xp acwxp

ϕχ

−−

∈

)

n−

∑



∈



(3)

где множество

⁭ (p,n) конструктивно определяется по p и n, а коэффициенты

находятся по коэффициентам a

. В работе [2] доказаны необходимые и

достаточные условии для того, чтобы функции вида (3) генерировали

адические кратномасштабные анализы в L

(⁭

В докладе будет дан обзор методов вычисления значений решений

уравнения (1), а для случаев

p = 2, 3, 4 приведены графики масштабирующих

функций и ортогональных вейвлетов в L

(⁭

). В частности, рассматриваются

итерационные, матричные и каскадные алгоритмы, определяемые по аналогии

с соответствующими методами для вейвлетов на прямой

⁭. Показано, что

основанные на разложениях (3) алгоритмы обладают рядом преимуществ

перед остальными методами вычисления значений функций

φ.

Литература

1. Lang W.C. Fractal multiwavelets related to the Cantor dyadic group //Intern. J.Math. and

Math. Sci. 1998.V. 21. P. 307-317.

2. Farkov Yu.A. On wavelets related to the Walsh series //J.Approx. Theory,

doi:10.1016/j.jat.2008.10.003, 2008.

206 S-XXVIII. Секция численных методов и математического моделирования

ПРИМЕНЕНИЕ МОНОТОННЫХ ЭРМИТОВЫХ СПЛАЙНОВ

В ЗАДАЧАХ ПАРАМЕТРИЗАЦИИ ГЕОЭЛЕКТРИЧЕСКИХ РАЗРЕЗОВ

ПРИ НЕЙРОСЕТЕВОЙ ИНТЕРПРЕТАЦИИ МТ ДАННЫХ

Е.А. Оборнев, М.И. Шимелевич, И.Е. Оборнев

Лаборатория «Геонейрон», НИИП РГГРУ, Москва, Россия

Эффективная интерпретация магнитотеллурических (МТ) данных с при-

менением нейросетевых методов может быть проведена в определенных клас-

сах геоэлектрических разрезов. Каждый такой k-й класс может быть построен

с помощью функции параметризации

),,,...,(

zyf

, которая преобразу-

ет набор макропараметров геоэлектрического разреза в распределение удель-

ной электропроводности на конечно-разностной сетке прямой задачи.

Простейшим примером параметризации является представление

электропроводности в виде линейной комбинации заданной системы функций

),( zy

(например, полиномов, сплайнов и др.) в исследуемой области

Ω∈=

∑

),(),,(),(σ

zyzyzy

ϕγ

В этом случае макропараметрами разрезов являются коэффициенты

соответствующих рядов. В общем случае функция параметризации, кроме

функций, заданных в явном виде, определяется с помощью правил и

алгоритмов, которые задают электропроводность среды в каждой точке

области (например, в случае слоистых сред с криволинейными границами

или сред, заданных с помощью блочных структур и т.д.).

При построении функции параметризации разреза возникает проблема

эффективной интерполяции в процессе пересчета макропараметров разреза на

микросетку прямой задачи. При использовании стандартных интерполирую-

щих сплайн-функций, как правило, появляются ложные экстремумы. В работе

предлагается использовать модифицированные сплайны Эрмита, обеспечи-

вающие выполнение условия монотонности между соседними узлами. Разра-

ботан алгоритм построения функции параметризации с применением моно-

тонных эрмитовых сплайнов для класса слоистых сред с криволинейными

границами. Предложенный подход иллюстрируется на модельных примерах,

подтверждающих эффективность применения сплайнов рассмотренного вида.

Разработанный алгоритм был использован для расчета баз данных эта-

лонных примеров решений прямых задач, предназначенных для обучения об-

ратных нейросетевых операторов (электронных нейросетевых палеток) в ме-

тоде МТ зондирования.

Представленная работа связана с прикладными задачами, решаемыми в

рамках научной тематики по гранту РФФИ № 09-05-01127-а.

Работа проведена на базе проблемной научно-исследовательской лабора-

тории «Геонейрон» в структуре научно-исследовательского института Приро-

допользования РГГРУ (НИИП РГГРУ).

S-XXVIII. Секция численных методов и математического моделирования 207

ОЦЕНКИ ГЛАДКОСТИ ДИАДИЧЕСКИХ МАСШТАБИРУЮЩИХ ФУНКЦИЙ

Е.А. Родионов, Ю.А. Фарков

РГГРУ имени Серго Орджоникидзе, Москва, Россия

Пусть − операция двоичного сложения на

⊕



В недавней работе [1]

найдены необходимые и достаточные условия, при выполнении которых диа-

дическое масштабирующее уравнение

() (2 ), ,

xcxk x

ϕϕ

−

=⊕∈

∑



(1)

имеет решение

)

∈



со следующими свойствами: 1)

2) система

supp [0, 2 ],

−

{( }):kk

⋅⊕ ∈



ортонормирована в 3)

 ),

генерирует

кратномасштабный анализ в

()L



Диадический модуль непрерывности

функции

определяется равенством

( , ) : sup{ ( ) ( ) : , [0,2 ),0 }, 0.

xy x xy y

ωϕδ ϕ ϕ δ δ

−

=⊕− ∈ ≤<>

Если функция

такова, что

(,2 ) 2 , ,

ωϕ

−−

≤∈



для некоторого

то существует константа

(, )C

такая, что

(,) (, ) .C

ϕδ ϕαδ

≤

(2)

Для данного решения

уравнения (1) обозначим через

точную

верхнюю грань множества всех значений

для которых выполнено не-

равенство (2).

Точные значения величины

в случаях

1, 2, 3n

приведены в работах

[1] − [3]. В настоящем докладе основное внимание будет уделено случаю

. В доказательствах оценок снизу существенно используются разложения

диадических масштабирующих функций в ряды Уолша (и в этом состоит глав-

ное отличие нашего метода от применяемых ранее методов оценки гладкости

вейвлетов и масштабирующих функций). Отметим, что алгоритм разложения

масштабирующих функций на

4n =



в лакунарные ряды Уолша был найден вто-

рым автором в [2], а из результатов статьи [1] следует применимость этого

алгоритма к любой финитной диадической масштабирующей функции про-

странства

()L

 .

Литература

1. Протасов В.Ю., Фарков Ю.А. Диадические вейвлеты и масштабирующие функции

на полупрямой // Матем. сборник. 2006. Т. 197. № 10. С. 129-160.

Фарков Ю.А. Ортогональные вейвлеты с компактными носителями на локально ком-

пактных абелевых группах» // Известия РАН. Сер. матем. 2005. Т. 69. № 3. С. 193-220.

3. Родионов Е.А., Фарков Ю.А. Об оценках гладкости диадических вейвлетов на полу-

прямой. В сб.: V Международный симпозиум «Ряды Фурье и их приложения». Тези-

сы докладов. Ростов-на-Дону: Изд-во ЦВВР, 2008. С. 48-49.

208 S-XXVIII. Секция численных методов и математического моделирования

КОНДЕНСАЦИЯ АТМОСФЕРНОЙ ВЛАГИ НА ПОВЕРХНОСТИ ЗЕМЛИ:

НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ФИЗИЧЕСКОГО

И МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Н.А. Рустамов, К.В. Чекарев

МГУ им. М.В.Ломоносова, Москва, Россия

Основной целью теоретических и экспериментальных работ при иссле-

довании конденсации паров воды из приземного слоя атмосферы на поверхно-

сти земли является достижение таких параметров процесса, при которых кон-

денсация может рассматриваться как нетрадиционный источник воды,

пригодный для практического использования.

Существующие математические модели, представляющие собой сложные

системы уравнений диффузии и теплопроводности, позволяют получить коли-

чественные оценки при различных температурных и влажностных режимах

атмосферы и подстилающей поверхности, но в силу ограниченности возмож-

ностей моделей не дают удовлетворительных ответов на многие вопросы, свя-

занные с изучением доступных механизмов влияния на количество конденси-

руемой влаги.

При подобном положении дел ценным дополнением к существующим

теоретическим положениям служат результаты, получаемые методом физиче-

ского моделирования. С целью экспериментального изучения конденсации при

искусственно регулируемых условиях разработана и построена лабораторная

модель, позволяющая в закрытой камере достичь условий конденсации и с

большой степенью точности измерить количество влаги, конденсирующейся

на водной поверхности. Проведен большой объем работ по измерению пара-

метров изучаемого процесса, позволивший построить экспериментальные кри-

вые зависимости количества конденсированной влаги от влажности и темпера-

туры воздуха. Экспериментальные работы с подобной точностью измерений

проведены впервые и расчеты, проведенные по полученным кривым, хорошо

согласуются с расчетами, проведенными по математическим моделям.

Построенные кривые могут быть использованы для изучения обратного про-

цесса – испарения. Развитие этих экспериментальных работ будет направлено

на исследование влияния внешних факторов (ветер, волнение, радиационное

излучение) на интенсивность конденсации, что позволит внести необходимые

дополнения в математические модели с учетом указанных факторов.

Полученные результаты могут быть применены к уточнению работ по

изучению водного баланса различных регионов земли и мирового океана, по-

скольку предварительные расчеты показали, что в этих работах не учитывает-

ся существенный вклад конденсации.

S-XXVIII. Секция численных методов и математического моделирования 209

ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ РИДЖЛЕТ-ПРЕОБРАЗОВАНИЯ

ПРИ ФИЛЬТРАЦИИ ГЕОФИЗИЧЕСКИХ ДАННЫХ

Н. В. Сорока

Российский Государственный Геологоразведочный Университет

имени Серго Орджоникидзе, Москва, Россия

Обработка геофизической информации – важнейший этап анализа экспе-

риментальных данных всех методов разведочной геофизики. Цель обработки –

извлечение полезной информации из результатов измерений полей, осложнен-

ных шумом различного происхождения. Подавление помех, выделения и раз-

деления полезных сигналов является актуальной задачей обработки полевых

материалов. Мы рассматриваем эффективность решения этой задачи посредст-

вом сравнительно новых математических методов, одним из которых является

риджлет-преобразование. Благодаря высокой эффективности алгоритмов мно-

гомасштабный анализ на основе риджлетов является мощным инструментом в

тех областях, где традиционно использовались другие методы анализа данных

(например, преобразование Фурье или вейвлет-преобразование). Наряду с дру-

гими возможными подходами, риджлеты являются надежным инструментом

анализа данных в частотно-временной области.

Риджлет-преобразование (ridgelet transform) комбинирует идеи много-

масштабного анализа, содержащиеся в вейвлет-преобразовании, с алгоритма-

ми выделения геометрических особенностей и структур посредством преобра-

зования Радона [1]. Достоинство применения риджлет-анализа объясняется его

впечатляющими возможностями к обнаружению произвольно ориентирован-

ных особенностей двумерных данных, с одной стороны, и относительной лег-

костью практического применения, с другой. С помощью этого преобразова-

ния удается существенно улучшить качество и достоверность результатов

обработки экспериментальных данных (например, выделить полезный сигнал,

осложненный шумом и случайными искажениями, подчеркнуть некоторые

особенности данных).

В докладе будут показаны фильтрационные возможности риджлет-

преобразования на примере фрагмента синтетической сейсмограммы, рассчи-

танной для модели горизонтально-слоистой среды и осложненной аддитивным

нормально распределенным «шумом» различной амплитуды. В результате об-

работки удалось существенно улучшать соотношение сигнал/шум и выделять

линейные объекты в сейсмическом сигнале.

Литература

1. Donoho D.L.,1998.

Ridge Functions and Orthonormal Ridgelets. Available:

http://www-stat.stanford.edu/Ridge-Ridgelet.pdf.

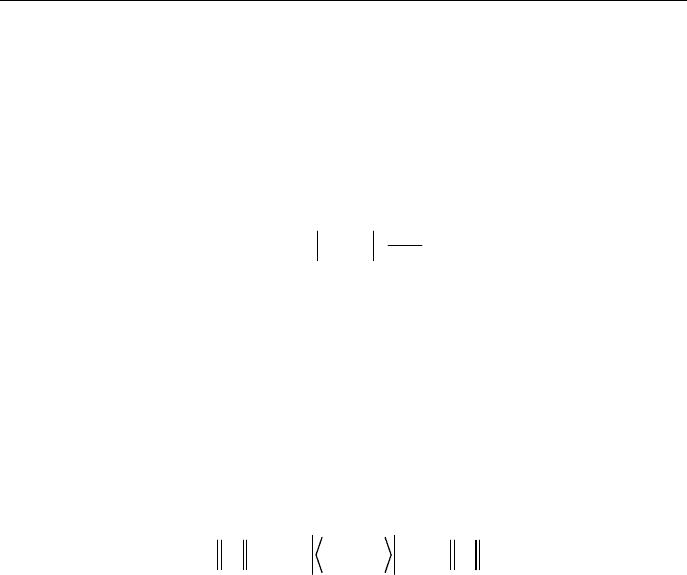
210 S-XXVIII. Секция численных методов и математического моделирования

О ДИАДИЧЕСКИХ ФРЕЙМАХ,

ОПРЕДЕЛЯЕМЫХ ПО ВЕЙВЛЕТАМ НА ПОЛУПРЯМОЙ

С.А. Строганов, Ю.А. Фарков

Российский Государственный Геологоразведочный Университет

имени Серго Орджоникидзе, Москва, Россия

Пусть

− преобразование Фурье-Уолша функции

(

)

∈



. Если

выполнено условие

0: ()

ψω

∫



+∞

то функция

называется вейвлетом в

(

)



. Для произвольного вейвлета

(

)

∈ 

и данного числа

{

}

0,1, 2s

∈

положим

:2 (2 2 ), , , ,

jj s

xkjk x

−

=⊕∈∈∈ 

где − операция двоичного сложения на (см., например, [1]). Система

⊕



{

}

является фреймом в

(

)



, если существуют положительные кон-

станты

такие, что для всех

(

)

fL∈



выполнены неравенства

ffB

≤≤

∑

)

В докладе будет сформулирован диадический аналог теоремы Добеши

([2], с.165) и с помощью этой теоремы построены примеры фреймов в

. Установлено, в частности, что при

(



≥

функции

, определяе-

мые условием

()

)

1, , ( 1) ,

0, ,( 1) ,

νν

ωα α

−−

⎧

⎡

∈+

⎪⎣

⎨

⎡

∉+

⎪

⎣

⎩

где

∈

, , являются жесткими фреймами в

l ∈

(

)



. Кроме того,

приведены примеры фреймов, конструируемые по двум масштабирующим

функциям в (см. теорему 2 в [3]).

(



)

Литература

Голубов Б.И. Элементы двоичного анализа. М.: Изд-во ЛКИ, 2007.

Малла С. Вэйвлеты в обработке сигналов. М.: Мир, 2005.

Фарков Ю.А. Биортогональные диадические вейвлеты на



// Успехи ма-

тем. наук. 2007. Т. 52. № 6. С. 189-190.