Ивченко Л.А. Эконометрия. Методические указания
Подождите немного. Документ загружается.

20
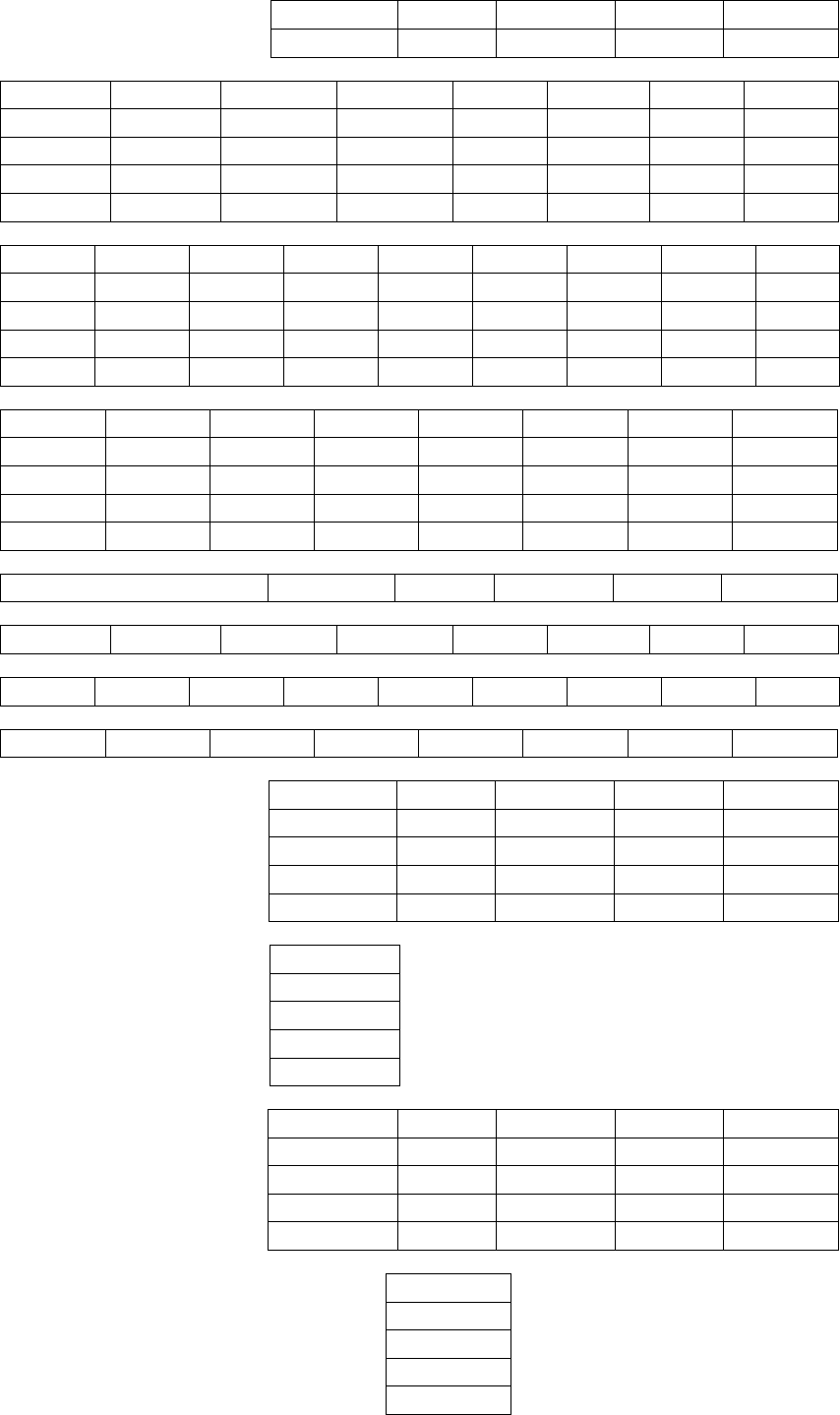
0,42 0,05 0,29 0,48 0,41
25,68 18,13 25,74 21,21 22,97
1 1 1 1 1 1 1 1
0,77 0,78 0,78 0,81 0,79 0,77 0,78 0,72
0,86 0,79 0,34 1,6 1,46 1,27 1,58 0,68
0,62 0,56 1,76 1,31 0,45 0,5 0,77 1,2
16,38 13,21 14,48 13,38 13,69 16,66 15,06 17,6
1 1 1 1 1 1 1 1 1
0,79 0,77 0,8 0,71 0,79 0,76 0,78 0,62 0,75
0,86 1,98 0,33 0,45 0,74 0,03 0,99 0,24 0,57
0,21 0,25 0,15 0,66 0,74 0,32 0,89 0,23 0,32
15,98 18,27 14,42 22,76 15,41 19,35 16,83 30,53 17,98
1 1 1 1 1 1 1 1
0,71 0,74 0,65 0,66 0,84 0,74 0,75 0,75
1,22 0,68 1 0,81 1,27 1,14 1,89 0,67
0,54 0,75 0,16 0,24 0,59 0,56 0,63 1,1
22,09 18,29 26,05 26,2 17,26 18,83 19,7 16,87
Y' = -0,66 1,41 -0,79 0,42 -0,24
1,89 0,36 1,18 2,18 1,44 1,55 0,09
1,9 1,43 2,39 -0,3 1,42 1 0,91 -1,76 1,12
0,03 0,55 -0,76 -0,78 1,72 0,61 0,5 0,61
30 22,29 27,48 17,16 571,01
22,29 16,6421
20,6397 12,9515 417,9802
27,48 20,6397
31,5096 15,8817 508,2342
17,16 12,9515
15,8817 14,0266 304,7835
X '
´
X =
571,01 417,9802
508,2342 304,7835
11439,537
20,83
16,9034
23,1993
12,2955
X '
´
Y =
278,3794
86,97678751
-89,6393
0,56379931
-1,339111
-1,0555998
-89,639283
94,09535
-0,8699556
0,9684084
1,0491616
0,563799306
-0,86996
0,17737098
0,0112619
-0,004536
-1,33911134
0,968408
0,01126195
0,3085579
0,0227372
(X'
´
X)
-1
=
-1,05559983
1,049162
-0,004536
0,0227372
0,0140394
-0,72472
7,134661
0,029368
-1,13958
A = (X'
´
X)
-1
´
(X'
´
Y) =
-0,17112
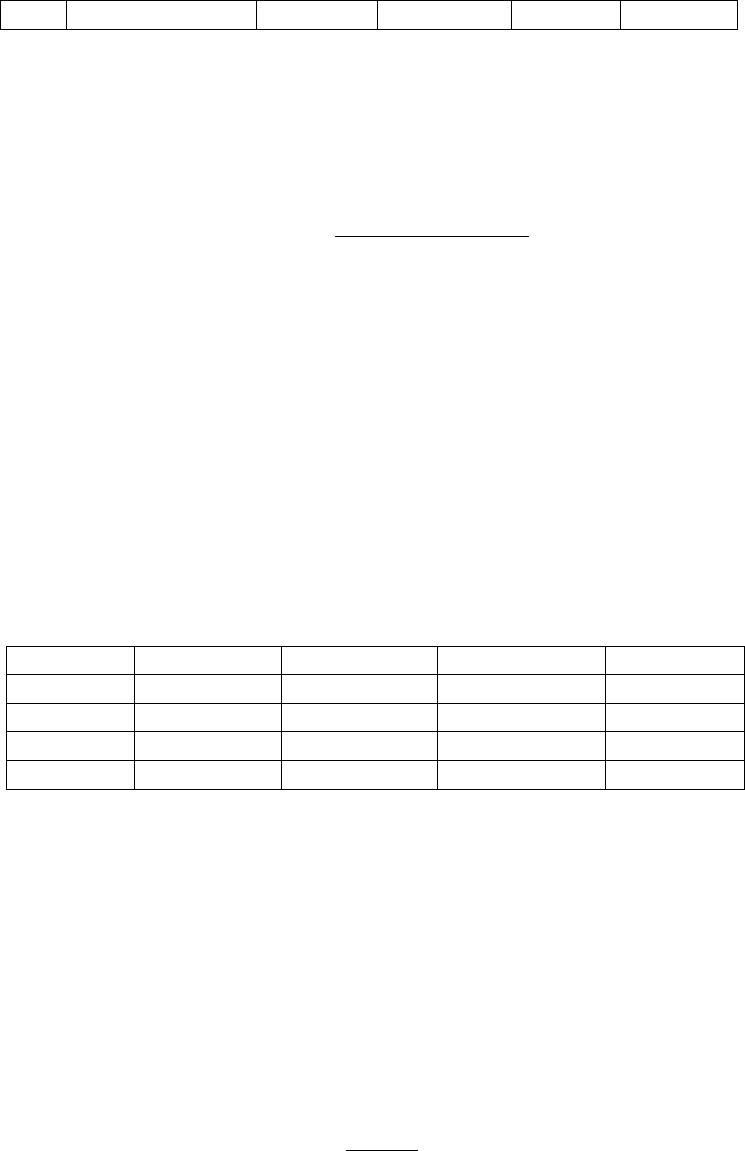
21
Рассчитав матрицу А, запишем четырехфакторную эконометриче-
скую модель:
y = – 0,72471539 + 7,13466087 x
1
+ 0,0293684 x
2
– 1,1395758 x
3
–
0,1711214 x
5
A' =
-0,72471539 7,134661 0,02936843
-1,139576
-0,1711214
2. Находим ковариационную матрицу для четырехфакторной модели.
Несмещенную оценку дисперсии остатков находим по формуле (2):
(
)
( )
mn -
´
´
-
´
=
)(
2
YX'A'YY'
s
e
,
где n – объем выборки исходных данных,
m – число переменных, входящих в эконометрическую модель,
(n – m) – число степеней свободы,
n = 30,
m = 5,
n – m = 25,
Y'
´
Y = 44,6961,
A'
´
(X'
´
Y)= 44,537194,
2
e
s
= 0,0063562.
Рассчитаем ковариационную матрицу:
0,5528437 -0,5697671 0,00358363 -0,0085117 -0,0067096
-0,569767 0,5980909 -0,0055296 0,0061554 0,0066687
0,0035836 -0,0055296 0,00112741 7,158E-05 -2,883E-05
-0,008512 0,0061554 7,1583E-05 0,0019613 0,00014452
-0,00671 0,0066687 -2,883E-05 0,0001445 8,9238E-05
Тогда дисперсии параметров новой модели:
,5528,0
2
0
=
s
b
s
2
1
b
= 0,5981,
s
2
2
b
= 0,0011,
s
2
3
b
= 0,0020,
s
2
5
b
= 8,924Е-05.
3. Воспользовавшись формулами (3) и (4), найдем множественный
коэффициент детерминации (скорректированный):
(
)
( )
1
σ
2
-
´
=
n
y
YY'
= 1,5412,

22
D = 1 –
s
s
e
2
2
y
= 0,9959.
Множественный коэффициент корреляции (скорректированный) R
удовлетворяет соотношению D = R
2
, поэтому:
R = 0,9979.
4. Проверим значимость (адекватность) четырехфакторной модели
по критерию Фишера:
При уровне значимости
a
= 0,05 и числах степеней свободы
k
1
= n – m = 25, k
2
= m – 1= 4 найдем по Приложению 1 критическое значение
F-критерия:
F
крит
(0,05; 4;25) = 5,77.
Так как F
набл
> F
крит
, делаем вывод о том, что модель значима с на-
дежностью не менее 95%.
5. Проверим значимость коэффициента корреляции с помощью t-
критерия. По формуле (6) находим:
По уровню значимости
a
= 0,05 и числу степеней свободы k = n – m =
25 найдем в Приложении 2 значение t-критерия:
t
крит
= 2,06.
Так как t
набл
> t
крит
, делаем вывод о том, что коэффициент корреля-
ции значим с надежностью не менее 95%.
6. Проверим значимость параметров модели. Для этого по формуле
(7) найдем наблюдаемое значение t-критериев:
24,1509
1
1
2
2
набл
=´=
-
-
-
m
mn
R
R
F
.5) 3, 2, 1, 0,(; == і
b
t
і
і
b
і
b
s
.70,77
1
2
набл
=
-
-
=
R
mnR
t

23
Тогда:
= 0,9747, = 9,2255,
= 0,8747,
= 25,7321,
= 18,1146.
Самый незначимый коэффициент b
2
.
Поэтому исключим фактор х
2
и рассчитаем трехфакторную эконо-
метрическую модель.
1. Нахождение оценок параметров трехфакторной модели методом
1МНК
x
1
x
3
x5 y
1 0,68 0,42 25,68 -0,66
1 0,74 0,05 18,13 1,41
1 0,66 0,29 25,74 -0,79
1 0,72 0,48 21,21 0,42
1 0,68 0,41 22,97 -0,24
1 0,77 0,62 16,38 1,41
1 0,78 0,56 13,21 1,89
1 0,78 1,76 14,48 0,36
1 0,81 1,31 13,38 1,18
1 0,79 0,45 13,69 2,18
1 0,77 0,5 16,66 1,44
1 0,78 0,77 15,06 1,55
1 0,72 1,2 17,6 0,09
1 0,79 0,21 15,98 1,9
1 0,77 0,25 18,27 1,43
1 0,8 0,15 14,42 2,39
1 0,71 0,66 22,76 -0,3
1 0,79 0,74 15,41 1,42
1 0,76 0,32 19,35 1
1 0,78 0,89 16,83 0,91
1 0,62 0,23 30,53 -1,76
1 0,75 0,32 17,98 1,12
1 0,71 0,54 22,09 0,03
1 0,74 0,75 18,29 0,55
1 0,65 0,16 26,05 -0,76
1 0,66 0,24 26,2 -0,78
1 0,84 0,59 17,26 1,72
1 0,74 0,56 18,83 0,61
1 0,75 0,63 19,7 0,5
X =
1 0,75 1,1 16,87
Y =
0,61
1 1 1 1 1
0,68 0,74 0,66 0,72 0,68
0,42 0,05 0,29 0,48 0,41
X' =
25,68 18,13 25,74 21,21 22,97
t
b
2
t
b
1
t
b
0
t
b
3
t
b
5
24
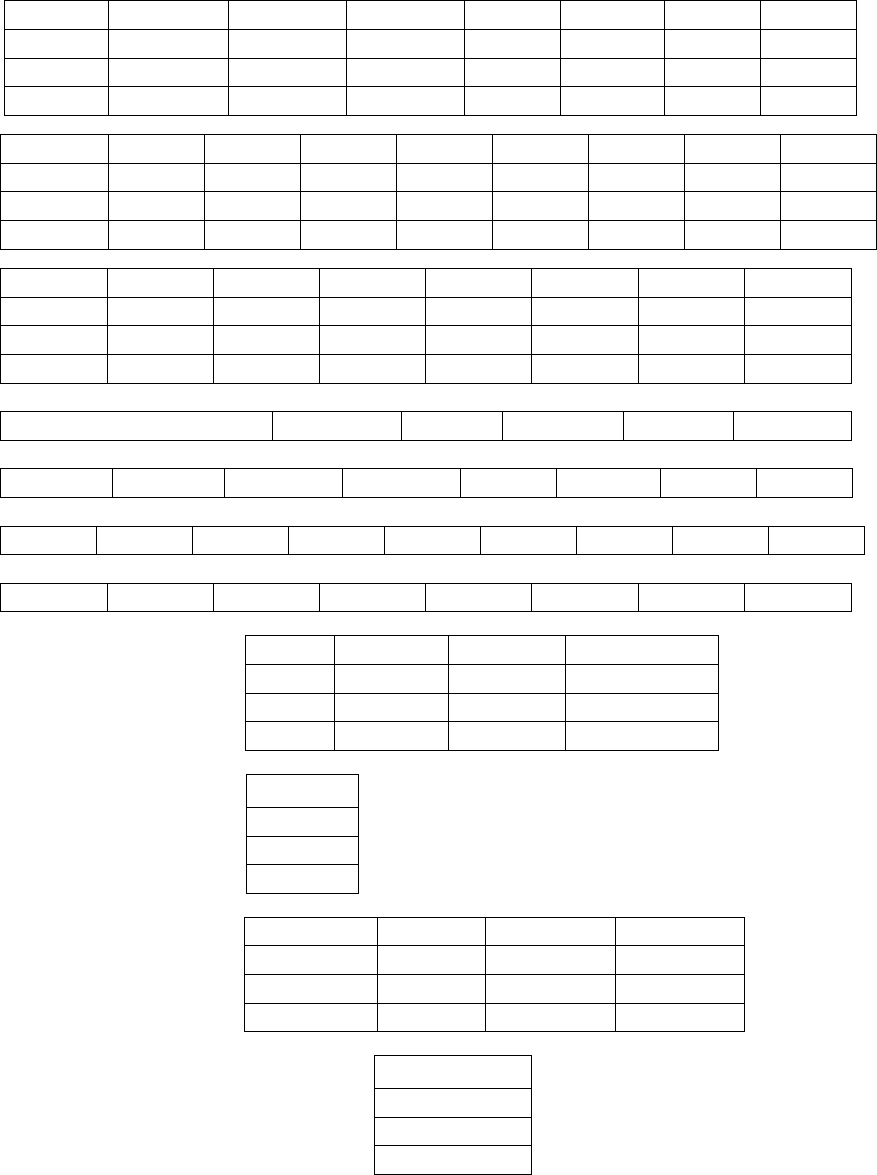
1 1 1 1 1 1 1 1
0,77 0,78 0,78 0,81 0,79 0,77 0,78 0,72
0,62 0,56 1,76 1,31 0,45 0,5 0,77 1,2
16,38 13,21 14,48 13,38 13,69 16,66 15,06 17,6
1 1 1 1 1 1 1 1 1
0,79 0,77 0,8 0,71 0,79 0,76 0,78 0,62 0,75
0,21 0,25 0,15 0,66 0,74 0,32 0,89 0,23 0,32
15,98 18,27 14,42 22,76 15,41 19,35 16,83 30,53 17,98
1 1 1 1 1 1 1 1
0,71 0,74 0,65 0,66 0,84 0,74 0,75 0,75
0,54 0,75 0,16 0,24 0,59 0,56 0,63 1,1
22,09 18,29 26,05 26,2 17,26 18,83 19,7 16,87
Y ' = -0,66 1,41 -0,79 0,42 -0,24
1,41 1,89 0,36 1,18 2,18 1,44 1,55 0,09
1,9 1,43 2,39 -0,3 1,42 1 0,91 -1,76 1,12
0,03 0,55 -0,76
-0,78 1,72 0,61
0,5 0,61
30 22,29 17,16 571,01
22,29 16,6421 12,9515 417,9802
17,16 12,9515 14,0266 304,7835
X '
´
X =
571,01 417,9802 304,7835 11439,537
20,83
16,9034
12,2955
X '
´
Y =
278,3794
85,18466995
-86,874 -1,3749091
-1,041182
-86,8740036
89,82845
1,02364511
1,0269139
-1,37490906
1,023645
0,30784282
0,0230252
(X'
´
X)
-1
=
-1,04118162
1,026914
0,02302524
0,0139234
-0,8180672
7,27870491
-1,1414405
A = (X'
´
X)
-1
´
(X'
´
Y) =
-0,1703704
Рассчитав матрицу А, запишем трехфакторную эконометрическую
модель:
y = – 0,81806721 + 7,27870491x
1
– 1,1414405x
3
– 0,1703704x
5.
2. Нахождение ковариационной матрицы для трехфакторной модели.
Опуская для упрощения формул знак «
´
», оценку дисперсии нахо-
дим по формуле (2):

25
)(
)(
2
mn -
¢
¢
-
¢
=
YXAYY
e
s
,
где n = 30,
m = 4,
n – m = 26,
Y' Y = 44,6961,
A'(X' Y)= 44,532332.
После расчетов, описанных выше, получим значение дисперсии остат-
ков:
s
e
2
= 0,0063.
Рассчитаем ковариационную матрицу:
0,5365594
-0,5472002
-0,0086602
-0,0065582
-0,5472 0,5658096
0,00644771
0,0064683
-0,00866 0,0064477
0,00193903
0,000145
(
)
=´´
-1
2
' XX
s
e
-0,006558 0,0064683
0,00014503
8,77E-05
Диагональные элементы матрицы определяют дисперсии параметров
модели:
s
2
0
b
= 0,5366,
s
2
1
b
= 0,5658,
s
2
3
b
= 0,0019,
s
2
5
b
= 8,77Е – 05.
3. Найдем множественный коэффициент детерминации по схеме, по-
казанной выше:
(
)
( )
1
'
2
-
´
=
n
y
YY
s
= 1,5412,
D = 0,9959.
Получим множественный коэффициент корреляции R:
D = R
2
,
R = 0,9979.
4. Проверим адекватность эконометрической модели с помощью F-
критерия. Находим наблюдаемое значение критерия:
.97,2111
1
1
2
2
набл
=×=
-
-
-
m
mn
R
R
F
При уровне значимости
a
= 0,05 и числах степеней свободы k
1
= n – m
= 26, k
2
= m – 1 = 3 найдем в таблицах значение F-критерия:

26
F
крит
(
a
;k
1
; k
2
) = 8,63.
Поскольку F
набл
> F
крит.
, делаем вывод об адекватности модели с на-
дежностью не менее 95%.
5. Проверим значимость коэффициента корреляции с помощью
t-критерия. Наблюдаемое значение критерия Стьюдента:
R
R
t
mn
2
набл
1-
=
-
= 79,598529.
По уровню значимости
a
= 0,05 и числу степеней свободы k
1
= n – m = 26
найдем в таблицах значение t-критерия:
t
крит
(0,05;26) = 2,05.
Так как t
набл
> t
крит
,
коэффициент корреляции значим с надежностью не
менее 95%.
6. Проверка значимости коэффициентов регрессии.
Рассчитаем:
і
і
і
b
b
b
t
s
= (і = 0,1,3,5),
t
b
0
= 1,1168,
t
b
1
= 9,6765,
t
b
3
= 25,9215,
t
b
5
= 18,1925,
Все коэффициенты с надежностью не менее 95% значимы.
7. Проведем интервальные оценки коэффициентов регрессии для
генеральной совокупности:
Воспользуемся формулой:
ii
biibi
tbtb
s
b
s
+
+
<
<
´
-
криткрит
(8)
и получим следующие оценки параметров генеральной совокупности:
-2,32374795 <=
0
b
<= 0,6876135
5,732528166 <=
1
b
<= 8,8248816
-1,23195466 <=
3
b
<= -1,0509263
-0,18962016 <=
5
b
<= -0,1511206
Проведенные оценки показывают значимость всех параметров модели.
Таким образом, описание экспериментальных результатов, представ-
ленных в табл. 2.1, может быть проведено в рамках трехфакторной модели.
27
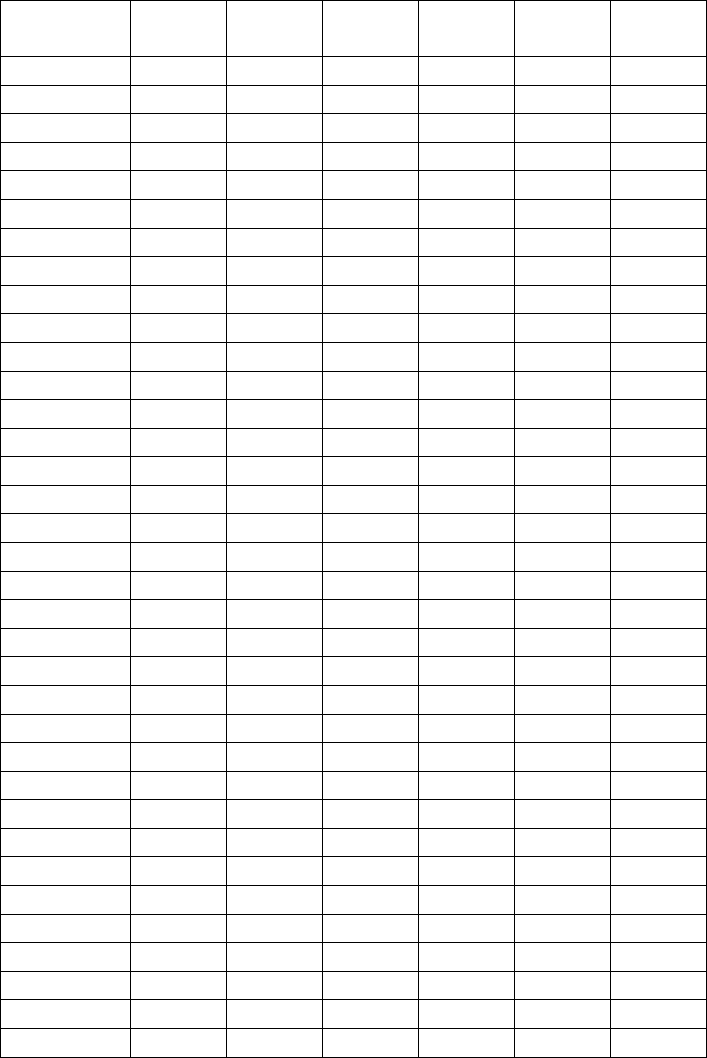
РАЗДЕЛ 3. ИССЛЕДОВАНИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ
СОГЛАСНО АЛГОРИТМУ ФАРРАРА–ГЛОБЕРА
Этот алгоритм содержит три вида статистических критериев проверки на-
личия мультиколлинерности:
а) всего массива переменных (критерий «хи-квадрат»);
б) каждой переменной с другими переменными (F-критерий);
в) каждой пары переменных (t-тест).
Предположим, имеются данные n = 35 наблюдений за поведением пере-
менной y в зависимости от изменений переменных х
1
, х
2
, х
3
, х
4
, х
5
. Требуется ус-
тановить наличие мультиколлинеарности в массиве переменных, который мож-
но представить в виде матрицы X размером 35
´
5 (из табл. 3.1).
Таблица 3.1
№
п/п
y
1
x
1
x
2
x
3
x
4
x
5
1 1,35 0,23 0,78 0,4 0,23 17,72
2 0,89 0,24 0,75 0,26 0,39 18,39
3 0,56 0,19 0,68 0,4 0,43 26,46
4 1,53 0,17 0,7 0,5 0,18 22,37
5 1,66 0,23 0,62 0,4 0,15 28,13
6 1,8 0,43 0,76 0,19 0,34 17,55
7 1,78 0,31 0,73 0,25 0,38 21,92
8 2,12 0,26 0,71 0,44 0,09 19,52
9 1,97 0,49 0,69 0,17 0,14 23,99
10 2,17 0,36 0,73 0,39 0,21 21,76
11 1,63 0,37 0,68 0,33 0,42 25,68
12 0,6 0,43 0,74 0,25 0,05 18,13
13 1,46 0,35 0,66 0,32 0,29 25,74
14 0 0,38 0,72 0,02 0,48 21,21
15 0,03 0,42 0,68 0,06 0,41 22,97
16 0,44 0,3 0,77 0,15 0,62 16,38
17 1,67 0,32 0,78 0,08 0,56 13,21
18 0,71 0,25 0,78 0,2 1,76 14,48
19 0,86 0,31 0,81 0,2 1,31 13,38
20 2,84 0,26 0,79 0,3 0,45 13,69
21 1,01 0,37 0,77 0,24 0,5 16,66
22 1,22 0,29 0,78 0,1 0,77 15,06
23 0,3 0,34 0,72 0,11 1,2 17,6
24 2,81 0,23 0,79 0,47 0,21 15,98
25 1,16 0,17 0,77 0,53 0,25 18,27
26 1,7 0,29 0,8 0,34 0,15 14,42
27 0,84 0,41 0,71 0,2 0,66 22,76
28 1,89 0,41 0,79 0,24 0,74 15,41
29 2,97 0,22 0,76 0,54 0,32 19,35
30 1,5 0,29 0,78 0,4 0,89 16,83
31 0,82 0,51 0,62 0,2 0,23 30,53
32 2,65 0,36 0,75 0,64 0,32 17,98
33 0,24 0,23 0,71 0,42 0,54 22,09
34 1,02 0,26 0,74 0,27 0,75 18,29
35 0,9 0,27 0,65 0,37 0,16 26,05

28
1. Для нормализации матрицы X потребуются средние значения и
средние квадратические отклонения каждой из независимых переменных х
1;
х
2
; х
3
; х
4
; х
5
. Среди функций математические находим СРЗНАЧ и
СТАНДОТКЛ и, воспользовавшись ими, находим необходимые значения и
заносим их в таблицу.
х
1
х
2
х
3
х
4
х
5
СРЗНАЧ
0,312857
0,734286
0,296571
0,473714
19,71314
СТАНДОТКЛ
0,087265
0,051007
0,14864 0,368735
4,502372
2. Нормализуем переменные. Для этого среди функций статистиче-
ские находим НОРМАЛИЗАЦИЯ. Каждая переменная нормализуется от-
дельно. Выделяем столбец 1
´
35 для переменной х
1
, в окна функции
НОРМАЛИЗАЦИЯ вносим последовательно массив исходных значений х
1,
затем среднее значение
x
*
1
, затем значение среднего квадратического откло-
нения. После ОК получаем столбец нормализованных данных х
1
. Повторяем
эту процедуру для каждой переменной. Получаем матрицу нормализованных
переменных X* (табл. 3.2).
Таблица 3.2
x
*
1
x
*
2
x
*
3
x
*
4
x
*
5
-0,94949 0,896241 0,695834 -0,66095 -0,44269
-0,8349 0,308083 -0,24604 -0,22703 -0,29388
-1,40787 -1,06429 0,695834 -0,11855 1,498512
-1,63706 -0,67218 1,368601 -0,79655 0,590102
-0,94949 -2,2406 0,695834 -0,87791 1,869427
1,342386 0,504136 -0,71698 -0,36263 -0,48045
-0,03274 -0,08402 -0,31332 -0,25415 0,490154
-0,60571 -0,47613 0,964941 -1,04062 -0,0429
2,029949 -0,86823 -0,85153 -0,90503 0,949912
0,540228 -0,08402 0,628557 -0,71519 0,454617
0,654822 -1,06429 0,224897 -0,14567 1,32527
1,342386 0,11203 -0,31332 -1,1491 -0,35162
0,425634 -1,45639 0,15762 -0,49823 1,338596
0,769416 -0,28008 -1,86068 0,017047 0,33246
1,227792 -1,06429 -1,59158 -0,17279 0,723365
-0,14733 0,700188 -0,98608 0,396724 -0,74031
0,081853 0,896241 -1,45702 0,234005 -1,44438
-0,7203 0,896241 -0,6497 3,488378 -1,16231
-0,03274 1,4844 -0,6497 2,267988 -1,40662
-0,60571 1,092294 0,023066 -0,06431 -1,33777
0,654822 0,700188 -0,38059 0,071286 -0,67812
-0,26193 0,896241 -1,32247 0,80352 -1,03349
0,311041 -0,28008 -1,25519 1,969671 -0,46934
-0,94949 1,092294 1,166771 -0,71519 -0,82915
-1,63706 0,700188 1,570431 -0,60671 -0,32053
-0,26193 1,288347 0,292173 -0,87791 -1,17563
1,113198 -0,47613 -0,6497 0,505203 0,676723
1,113198 1,092294 -0,38059 0,722161 -0,95575
-1,06409 0,504136 1,637708 -0,41687 -0,08066
X*=
-0,26193 0,896241 0,695834 1,128958 -0,64036
29
2,259137 -2,2406 -0,6497 -0,66095 2,402479
0,540228 0,308083 2,310476 -0,41687 -0,38494
-0,94949 -0,47613 0,830387 0,179765 0,527912
-0,60571 0,11203 -0,17876 0,749281 -0,31609
-0,49112 -1,65244 0,494004 -0,85079 1,407448
3. Транспонируем нормализованную матрицу X*. Для этого выделим
массив 5
´
35 и воспользуемся функцией ТРАНСП в списке полный алфа-
витный перечень
-0,94949 -0,8349 -1,40787 -1,63706 -0,949491,342386 -0,03274
0,8962410,308083 -1,06429 -0,67218 -2,24060,504136 -0,08402
0,695834 -0,246040,6958341,3686010,695834 -0,71698 -0,31332
-0,66095 -0,22703 -0,11855 -0,79655 -0,87791 -0,36263 -0,25415
X*'=
-0,44269 -0,293881,4985120,5901021,869427 -0,480450,490154
-0,605712,0299490,5402280,6548221,3423860,4256340,7694161,227792-0,14733
-0,47613-0,86823-0,08402-1,064290,11203-1,45639-0,28008-1,064290,700188
0,964941-0,851530,6285570,224897-0,313320,15762-1,86068-1,59158-0,98608
-1,04062-0,90503-0,71519-0,14567 -1,1491-0,498230,017047-0,172790,396724
-0,04290,9499120,4546171,32527-0,351621,3385960,332460,723365-0,74031
0,081853 -0,7203-0,03274-0,605710,654822-0,261930,311041-0,94949-1,63706
0,8962410,896241 1,48441,0922940,7001880,896241-0,280081,0922940,700188
-1,45702 -0,6497 -0,64970,023066-0,38059-1,32247-1,255191,1667711,570431
0,2340053,4883782,267988-0,064310,0712860,803521,969671-0,71519-0,60671
-1,44438-1,16231-1,40662-1,33777-0,67812-1,03349-0,46934-0,82915-0,32053
-0,261931,113198
1,113198
-1,06409
-0,26193
2,259137
0,540228
-0,94949
-0,60571
-0,49112
1,288347-0,47613
1,092294
0,504136
0,896241
-2,2406 0,308083
-0,47613
0,11203 -1,65244
0,292173-0,6497 -0,38059
1,637708
0,695834
-0,6497 2,310476
0,830387
-0,17876
0,494004
-0,877910,505203
0,722161
-0,41687
1,128958
-0,66095
-0,41687
0,179765
0,749281
-0,85079
-1,175630,676723
-0,95575
-0,08066
-0,64036
2,402479
-0,38494
0,527912
-0,31609
1,407448
4. Перемножаем матрицы Х*' и Х*. Для этого выделим массив 5
´
5 и
воспользуемся функцией МУМНОЖ:
34 -7,46528 -18,6151 -1,64623 6,609819
-7,46528 34 -0,65761 12,97553 -32,4687
-18,6151 -0,65761 34 -13,5573 4,349731
-1,64623 12,97553 -13,5573 34 -15,1739
Х*'
´
Х* =
6,609819
-32,4687 4,349731 -15,1739 34
5. Находим корреляционную матрицу r. Для этого матрицу, получен-
ную в предыдущем пункте, умножаем на 1/(n – 1). В данном случае число
