Ивченко Л.А. Эконометрия. Методические указания

ДОНЕЦКИЙ ИНСТИТУТ ТУРИСТИЧЕСКОГО БИЗНЕСА

К.ф.-м.н. Л.А. Ивченко

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к решению задач по дисциплине

«ЭКОНОМЕТРИЯ»

Донецк 2005

ББК 65.05я73

И 25

Рецензент

Крапивина Г.А.

Ивченко Л.А.

И 25 Методические указания к решению задач по дисциплине

«Эконометрия» / Донец. ин-т турист. бизнеса. – Донецк, 2005. – 73 с.

В пособие включены примеры решения основных задач эконометрии

по темам, изучаемым в рамках программы, принятой в Украине для студен-

тов, обучающихся по специальности «Менеджмент организаций». Четыре из

пяти предлагаемых задач решаются с помощью электронных таблиц Excel.

Издание содержит варианты заданий для выполнения самостоятельных работ

и может быть рекомендовано студентам экономических и гуманитарных спе-

циальностей.

ББК 65.05я73

туристического бизнеса, 2005

Рекомендовано к публикации и внедрению

в учебный процесс методическим советом ДИТБ

(протокол №

7

от

08.06.

2005

г.)

3

ОГЛАВЛЕНИЕ

РАЗДЕЛ 1. ПОСТРОЕНИЕ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ ...............4

РАЗДЕЛ 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ...............................................12

РАЗДЕЛ 3. ИССЛЕДОВАНИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ СОГЛАСНО

АЛГОРИТМУ ФАРРАРА–ГЛОБЕРА...............................................................27

РАЗДЕЛ 4. ТЕСТИРОВАНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ

(ПАРАМЕТРИЧЕСКИЙ ТЕСТ ГОЛЬДФЕЛЬДА – КВАНДТА)....................34

РАЗДЕЛ 5. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА–ДУГЛАСА ........38

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ........................................44

СПИСОК ЛИТЕРАТУРЫ ..................................................................................72

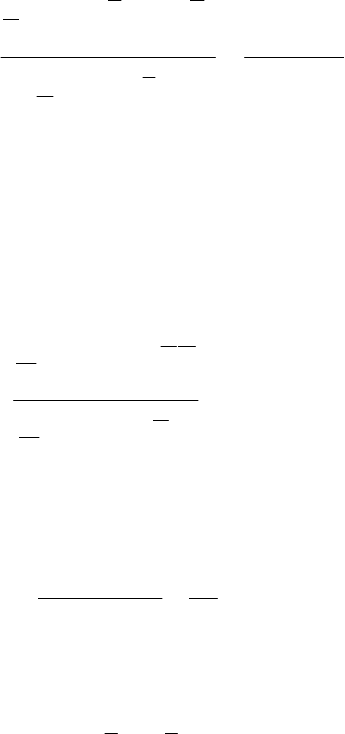
4

РАЗДЕЛ 1. ПОСТРОЕНИЕ ПРОСТОЙ ЛИНЕЙНОЙ

РЕГРЕССИИ

В качестве исходных данных в табл. 1.1 представлены наблюдаемые

значения x

і

(независимая переменная) и y

і

(зависимая переменная). Число из-

мерений n = 5. В столбцах 3 – 13 помещены промежуточные расчеты, необ-

ходимые для определения параметров и анализа полученного уравнения про-

стой линейной регрессии. Для удобства дальнейших расчетов в таблице пла-

нируем столбцы (колонки) для вычислений и нумеруем их.

1. Первый этап построения модели простой линейной регрессии

xbby

10

ˆ

+=

состоит в расчете параметров

1

b и

0

b . Параметры определяем на основании

метода наименьших квадратов (МНК), который требует минимизации суммы

квадратов отклонений (ошибок) наблюдаемых значений

і

y от расчетных

і

y

ˆ

[1, 2].

Вначале определяем параметр

1

b (наклон) прямой по формуле:

×=

-

--

=

å

=

)var(

);(cov

)(

1

))((

1

2

1

x

yx

xx

n

yyxx

n

b

n

i

n

i

ii

(1)

Здесь в числителе – ковариация между переменными x и y, в знамена-

теле – вариация (дисперсия) переменной х.

Для расчетов удобнее пользоваться второй формулой для определения

1

b , внося в нее данные из табл. 1.1:

()

×

-

=

å

=

n

i

n

i

ii

xx

n

yxyx

n

b

1

2

1

(2)

Для нашего примера получим (см. столбцы 1; 2; 3 и 4):

×==

-

×

-

= 3

22

66

10

122

4010466

2

1

b

Зная

1

b , находим второй параметр регрессии

0

b (отсечение):

xbyb

10

-=

. (3)

5

Таблица 1.1

i

y

i

x

2

i

x

ii

yx

yy

i

-

2

)( yy

i

-

i

y

ˆ

ii

yy

-

ˆ

2

)

ˆ

(

ii

yy -

yy

i

-

ˆ

2

)

ˆ

( yy

i

-

xx

i

-

2

)( xx

i

-

№

п/п

1 2 3 4 5 6 7 8 9 10 11 12 13

1

25 5 25 125 -15 225 25

0 0 -15 225 -5 25

2

30 6 36 180 -10 100 28

-2 4 -12 144 -4 16

3

35 9 81 315 -5 25 37

2 4 -3 9 -1 1

4

45 12

144 540 5 25 46

1 1 6 36 2 4

5

65 18

324 1170 25 625 64

-1 1 24 576 8 64

å

200 50

610 2330 0 1000 10 990 110

å

n

40 10

122 466 0 200

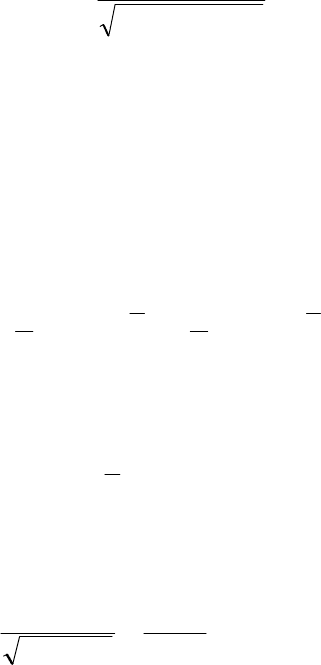
6

Для рассматриваемого примера получим (см. столбцы 1; 2; 3 и 4)

1010340

0

=

´

-

=

b

.

Таким образом найдено уравнение простой линейной регрессии, или,

другими словами, построена математическая модель простой линейной рег-

рессии:

103

ˆ

+

=

xy

. (4)

2. Пользуясь уравнением (4), получим расчетные значения

i

y

ˆ

и зане-

сем их в 7-й столбец таблицы:

.6410183

ˆ

,4610123

ˆ

,371093

ˆ

,281063

ˆ

,251053

ˆ

5

4

3

2

1

=+´=

=

+

´

=

y

3. Далее рассчитываем и записываем результаты во все остальные

столбцы таблицы с 8-го по 13-й согласно их наименованиям.

4. Считаем коэффициент корреляции по формуле:

() ()

×

´

=

yx

R

varvar

);cov(

(5)

Значения ковариации между переменными x и y и дисперсии x были

найдены в п. 1:

,66);cov(

=

yx

22)var(

=

x (см. формулы (1) и (2)).

Дисперсию для переменной у находим по формуле:

(

)

åå

==

-=-=

n

i

n

i

yy

n

yy

n

y

1

2

1

2

.)(

11

)var(

Воспользовавшись данными столбцов 1 и 6, получим:

.2001000

5

1

)var( ==y

Подставляя все данные в формулу (5), находим значение коэффициента

корреляции:

.995,0

23,66

66

20022

66

»=

´

=R

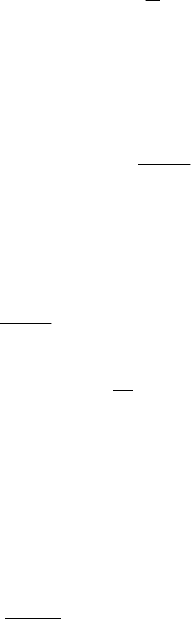
7

Заметим, что получен результат, близкий к R=1, поэтому можно гово-

рить о сильной корреляционной зависимости между переменными х и y.

5. Находим коэффициент детерминации

2

R

:

.99,0)995,0(

22

==R

6. Проверяем построенную модель простой линейной регрессии на аде-

кватность по критерию Фишера.

Вспоминаем [3, 4], что с помощью критерия Фишера проверяется ста-

тистическая гипотеза о равенстве дисперсий. В нашем случае с помощью

F-критерия Фишера проверяется гипотеза о неадекватности модели. Для это-

го сравниваются средний квадрат отклонений, который можно пояснить, ис-

ходя из уравнения регрессии, и средний квадрат ошибок. Тогда нулевая и

конкурирующая гипотезы формулируются следующим образом:

Н

0

– построенная модель неадекватна и наблюдаемые значения пере-

менных лучше описывать средним значением

y

;

Н

1

– построенная модель адекватна и соответствует действительности,

т. е. хорошо описывает экспериментальные данные.

Наблюдаемые значения критерия рассчитываем по формуле:

MSE

MSR

тnmF =-- );1(

набл

, (6)

где m – общее число оцениваемых параметров;

n – число наблюдений;

MSR – средняя сумма квадратов отклонений, обусловленных регрессией,

;

1

-

=

m

SSR

MSR (7)

2

1

)( yySSR

i

n

i

-=

å

=

)

(8)

– сумма квадратов отклонений (sum square regration), поясняющих регрессию

с (m – 1) числом степеней свободы;

MSE – средняя сумма квадратов отклонений, обусловленных неучтен-

ными факторами (ошибками):

;

mn

SSE

MSE

-

=

(9)

2

1

)(

i

n

i

yySSE -=

å

=

)

(10)

– сумма квадратов ошибок (sum square error) с (n – m) степенями свободы.

Воспользовавшись данными 9-го и 11-го столбцов и формулами (7) –

(10), для нашего примера находим:

8

990

1

2

990

=

-

=MSR

,

33,3

3

10

2

5

10

»=

-

=MSE

.

Тогда

300

33,3

990

набл

»=F

.

По уровню значимости

a

=0,05 и числу степеней свободы m – 1 = 1 и

n – m = 3 по таблице критических точек Фишера (Приложение 1) находим:

13,10)3;1;05,0(

крит

=

F .

Строим критическую область и сравниваем наблюдаемое и критиче-

ское значения F – критерия (рис. 1).

______________________________________________________________

F

крит

= 10,13 F

набл

= 300

Рис. 1. Правосторонняя критическая область для критерия Фишера F

крит

=10,13

В данном случае F

набл

> F

крит

попадает в критическую область, значит,

нулевая гипотеза H

0

о неадекватности модели отвергается. Модель y = 3x +

10 адекватна.

7. Проверяем значимость параметров b

0

и b

1

, определенных МНК, с

помощью t-теста Стьюдента.

Выдвигаем нулевую и конкурирующую гипотезы:

Н

0

: b

0

= 0; b

1

= 0, т.е. параметры не значимы,

Н

1

: b

0

¹

0; b

1

¹

0 – параметры значимы.

Для проверки статистической гипотезы находим дисперсии параметров

2

0

b

s

и

2

1

b

s

, которые определяются через дисперсию случайной величины

2

e

s

:

å

-

´=

2

22

)(

0

xxn

x

i

b

e

ss

;

å

-

´=

2

22

)(

1

xх

i

b

e

ss

; (11)

9

×

-

=

å

2

)(

2

n

yy

ii

)

e

s

(12)

Наблюдаемые значения t-критерия будем находить по формулам:

s

0

b

t

=

,

s

1

b

t

=

. (13)

По данным 9-го столбца таблицы 1.1 и формуле (12) находим диспер-

сию ошибок:

3

10

2

5

10

2

=

-

=

e

s

.

Добавляя данные 3-го и 13-го столбцов, по формулам (11) получаем:

;697,3

110

5

3

61010

2

0

»

´´

´

=

s

b

.03,0

110

3

10

2

1

»

´

=

s

b

Извлекая квадратные корни из дисперсий, получаем средние квадрати-

ческие отклонения для параметров:

1,923,

2

0

»=

b

s

0,173

2

1

»=

b

s

.

Находим наблюдаемые значения t-критерия для обоих параметров по

формулам (13):

2,5

923,1

10

0

»»

t

b

,

.24,17

173,0

3

1

»»

t

b

По таблице критических точек Стьюдента (Приложение 2) находим t

крит

по уровню значимости

025,0

2

=

a

(двусторонняя критическая область) и

(n – 2) степеням свободы:

t

крит

(

2

a

; n – 2) = t

крит

(0,025; 5 – 2) = t

крит

(0,025; 3) = 3,182.

Строим двустороннюю критическую область и сравниваем наблюдае-

мые и критические значения t-критерия Стьюдента (рис.2):

Ивченко Л.А. Эконометрия. Методические указания

Подождите немного. Документ загружается.