Ивания С.П. Математическое моделирование физических процессов
Подождите немного. Документ загружается.


31
Эту проблему понимают достаточно отчетливо не только специалисты, и
много предложений и конкретных действий уже направлено на ее преодоле-
ние. Однако вторая проблема еще не получила достаточного внимания и ши-
рокой огласки – это проблема возможной потери стабильности биосферы как
целостной системы, частью которой является человечество. Параметры био-
сферы имеют довольно узкий диапазон значений, в котором может существо-
вать наш биологический вид. Последние столетия биосфера подвергается все
возрастающим антропогенным нагрузкам. Особое значение имеют нагрузки,
связанные с вовлечением в биосферные циклы ископаемых энергоносителей –
углеводородов и ядерного горючего. Все большее количество органики чело-
вечество превращает в отбросы, при этом компенсационные возможности био-
сферы либо уже нарушены, либо находятся на пределе своих возможностей.
Если биосфера действительно начинает терять свою способность компенси-
ровать внешние возмущения, и ее характеристики уже стали отличаться от тех
квазиравновесных значений, которые были ей свойственны в течение многих
столетий, то это означает, что возникла необратимая рассогласованность, ко-
торая будет расти и дальше. Причем рост этот, как и при всякой потере устой-
чивости – экспоненциальный. Если такая система, как биосфера, теряет ста-
бильность, то начинается ее необратимый переход в некоторое новое квази-
стабильное состояние, и заранее неизвестно, окажутся ли параметры биосферы
в этом новом состоянии пригодными для существования человека. Где же вы-
ход из этой ситуации? Человечество должно осознать, что биосфера и человек
– это единая система, и человек обязан, используя свои знания, проводить ис-
следования развития этой системы, определив при этом границы допустимой
техногенной деятельности человека. Получение таких знаний – это одна из
задач, вторая задача – доведение этих знаний до всех жителей Земли и пере-
стройка жизни по новым канонам, которые позволят сохранить устойчивость
системы.
8.2 Нелинейные модели динамических систем
Динамическая система – это система, находящаяся в развитии. Причины, по-
буждающие систему к развитию, могут быть как внутренними, так и внешними.
Если функция, описывающая поведение системы, является линейной относитель-
но аргумента функции, то система линейна. Большинство же явлений природы по
сути своей нелинейны. При этом нелинейные эффекты играют большую роль в
задачах теоретической экологии.
Рассмотрим динамическую экологическую систему, которая представляет
собой некоторую биологическую популяцию, численность которой x(t) эволю-
ционирует во времени. Пусть это будет изолированная от других популяций сис-
тема, в которой нет сколько-нибудь заметной борьбы за существование (напри-
мер, за ограниченные ресурсы), и рост численности популяции в течение некото-
рого промежутка времени ничем не ограничен (по истечении этого времени по-
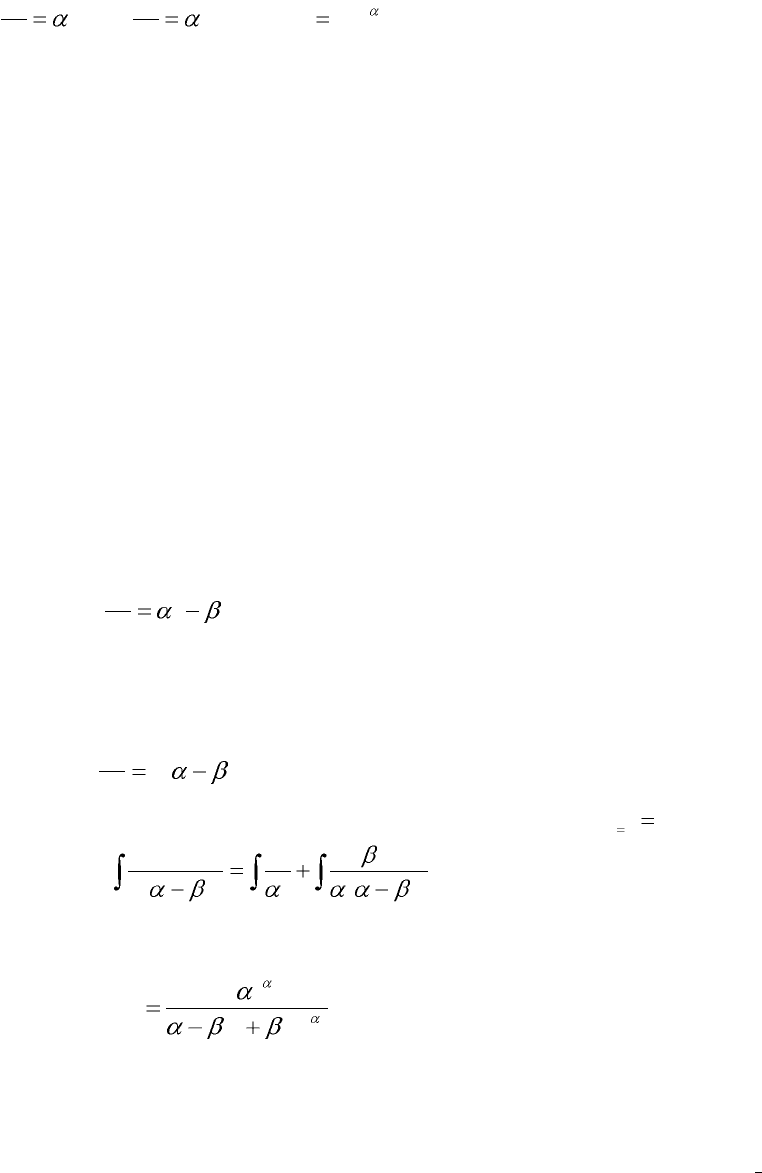
32
пуляция полностью уничтожается). При таких условиях применим закон Мальту-
са, согласно которому скорость приращения численности популяции пропорцио-
нальна ее текущим размерам:
t
extxdt
x
dx
x
dt
dx
0
)(;;
(1)
Для этого промежутка времени мы получили неограниченный рост популяции во
времени. Коэффициент α называется приведенным коэффициентом рождаемо-
сти. Примерно такую модель Мальтус применил к человеческому сообществу, и
так как ресурсы на планете Земля ограничены, он сделал вывод о том, что демо-
графический рост опережает рост производства продуктов питания. Последствия
перенаселенности известны: эпидемии, борьба за ограниченные ресурсы (войны)
и т.п. Причем в целом для человечества массовая гибель людей в результате та-
ких катаклизмов может даже рассматриваться как благо.
Однако рассмотренная модель слишком упрощенно описывает скорость
прироста популяции. На самом деле уже факт роста популяции естественным пу-
тем приводит к изменению исходного уравнения (1), т.к. возросшая концентра-
ция неизбежно приводит к парным взаимодействиям. Эпидемии в результате
взаимных контактов, борьба за ресурсы, преступность – это все примеры парных
взаимодействий, уменьшающих скорость роста популяции. Эти эффекты парных
взаимодействий должны учитываться квадратичным членом:
2
xx
dt
dx
(2)
где β называют приведенным коэффициентом смертности. Уравнение (2) в тео-
рии нелинейных систем носит название логистического уравнения. Оно может
быть приведено к виду
)( xx
dt
dx
(3)
и проинтегрировано в аналитическом виде при начальном условии:
00
xx
t
.
)()( x
dx
x
dx
xx
dx
Результат интегрирования с учетом начального условия приводит к следующей
зависимости роста популяции со временем:
t
t
exx
ex
tx
00
0
)(
(4)
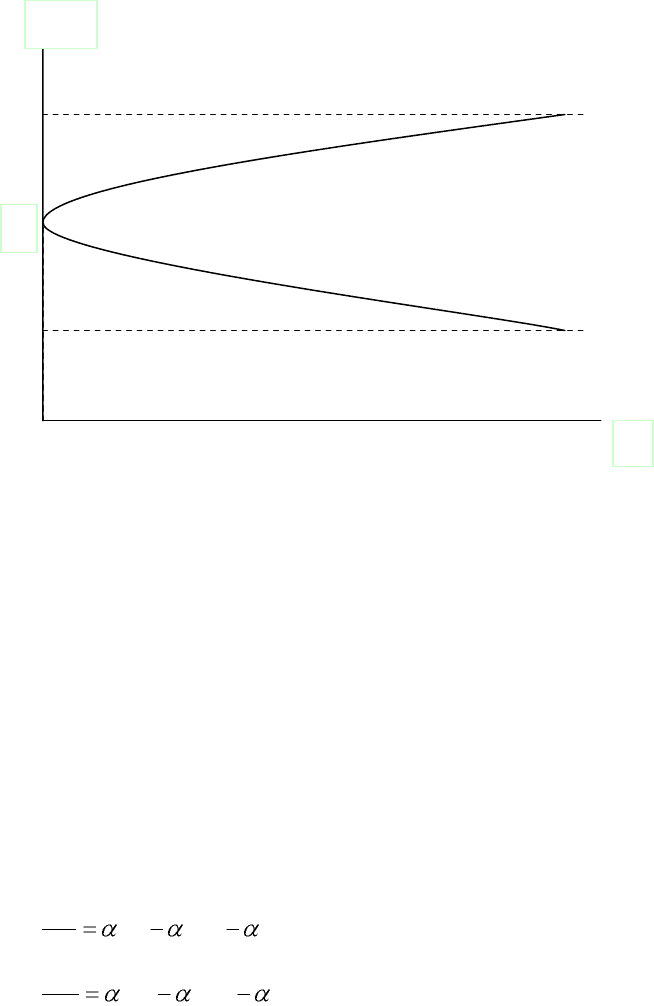
Если принять начальную населенность за единицу, то результат исследования по-
лученной формулы дает: при t = 0 x = x
0
, при t → ∞ x → α/β. Итак, все зависит
от соотношения приведенных коэффициентов рождаемости и смертности. Если
рождаемость превышает смертность, населенность растет, приближаясь к своему
пределу α/β > 1; если же ситуация обратная, то населенность падает, но не до ну-
ля, а до некоторого конечного предела
α/β < 1.
33
Рис. 1 Развитие численности популяции во времени при различных соотношениях
коэффициентов рождаемости и смертности.
Следующий шаг в приближении модели к действительности состоит в
учете конкуренции со стороны других популяций. Для начала рассмотрим две
конкурирующие популяции х
1
и х
2
. Конкуренция видов означает, что каждый из
них стремится подавить другой вид, т.е. в уравнения для скорости прироста кро-
ме парных нужно ввести перекрестные взаимодействия. Тогда вместо уравнения
(3) придем к системе двух уравнений:
1221
2
22222
2
2112
2
11111
1
xxxx
dt
dx
xxxx
dt
dx
(5)
Здесь α
1
, α
11
– коэффициенты рождаемости и смертности первой популя-
ции соответственно, α
12
– коэффициент подавления первой популяции со стороны
второй. Аналогичный смысл имеют коэффициенты второго уравнения в системе
α/β
1
t
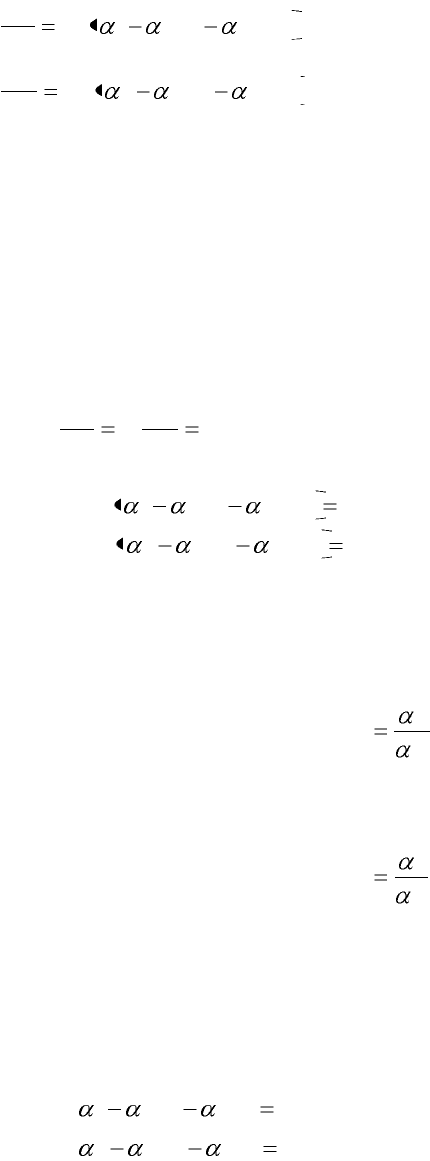
34
(6). Можно записать эти уравнения в более симметричной форме:
12122222
2
21211111
1
xxx
dt
dx
xxx
dt
dx
(6)
Чтобы получить зависимость от времени численностей популяций х
1
и х
2
, нужно
решить систему (6) с заданными коэффициентами (все коэффициенты положи-
тельны) и начальными условиями. Судьба популяции будет зависеть от величин
соответствующих коэффициентов рождаемости, смертности и подавления. По-
пробуем рассмотреть предельные стационарные состояния для х
1
и х
2
, т.е. поло-
жим
.0,0
21
dt
dx
dt
dx
Соответственно получим два уравнения:
0
0
12122222
21211111
xxx
xxx
(7)
Уравнения (7) имеют следующие решения:
1) х
1
=0 (популяция х
1
уничтожена); тогда вторая популяция достигает своего
предельного значения
22
2
2
x
;
2) х
2
=0 (популяция х
2
уничтожена); тогда первая популяция достигает своего
предельного значения
11
1
2
x
; эти случаи соответствуют крайне антагони-
стическим ситуациям, когда один из видов вымирает, а другой достигает
своей равновесной численности; однако существует и третье стационарное
состояние –
3)
0
0
1212222
2121111
xx
xx
(8)
В координатах х
2
–х
1
точки стационарных состояний популяции 1 лежат на пря-
мой I (получена из первого из уравнений (8)), точки стационарных состояний по-
пуляции 2 лежат на прямой II (второе из уравнений (8)), а точка пересечения этих
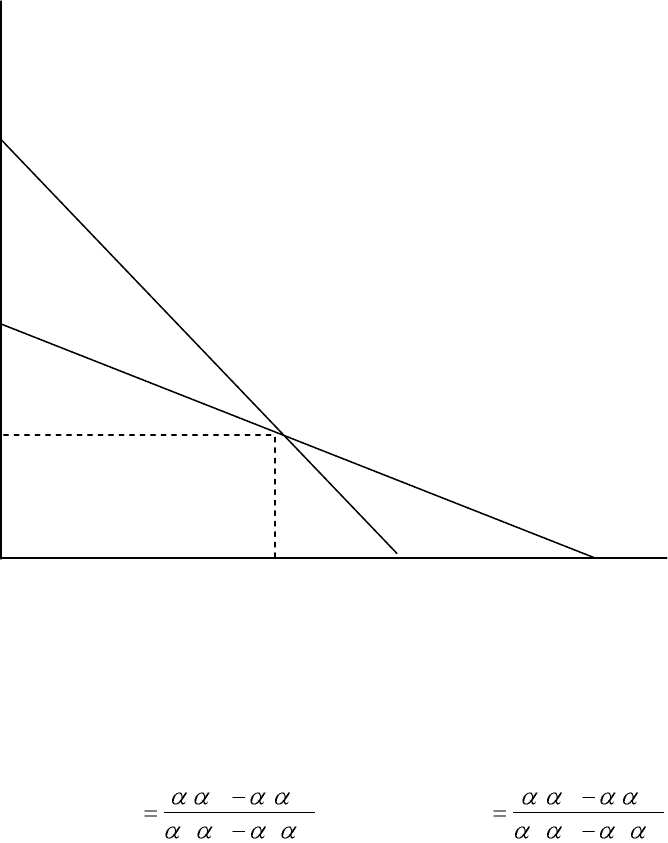
35
прямых дает точку устойчивого равновесия обеих популяций («мирное сосущест-
вование»).
Х
2
I
II
Х
2
*
Х
1
Х
1
*
1
Рис.2 Стационарные состояния и точка устойчивого равновесия популяций
Координаты точки устойчивого равновесия двух популяций получены из реше-
ния системы (8):
12211122
122221
*
1
X
;
12211122
211112
*
1
X
.
Для большего количества популяций система уравнений будет содержать боль-
шее количество уравнений и коэффициентов, оценить правдоподобные значения
которых задача не из легких, как и само моделирование экологических ситуаций.
Тем не менее такие модели существуют, совершенствуются и анализируются на
предмет соответствия их действительности.
