Ивания С.П. Математическое моделирование физических процессов
Подождите немного. Документ загружается.

1
Ивания С.П.
Конспект лекций по дисциплине «Математическое моделирование физиче-
ских процессов».
Тема 1. Математическое моделирование и вычислительный эксперимент.
1.1 Введение
Большое количество физических задач формулируется в виде уравнений
математической физики, получить решение которых в аналитическом виде чаще
всего не удается. Это связано со сложностью исследуемых проблем. Например, в
задачах аэродинамики при сверхзвуковых скоростях полета летательных аппара-
тов (ЛА) возникают сопутствующие задачи газовой динамики, теплопереноса,
теплозащиты ЛА при высоких температурах и т.п. Чисто теоретическое исследо-
вание этих вопросов затруднено из-за сложности физических явлений и матема-
тического аппарата, применяемого для их описания. Экспериментальное иссле-
дование в натурных условиях также представляет большие трудности. Широко
применяется физическое моделирование в лабораторных условиях, сложность
которого состоит в создании адекватной модели и необходимости использования
дорогостоящего оборудования.
На практике все эти методы исследования применяются в совокупности, а в
последние годы в связи с бурным развитием вычислительной техники широкое
распространение получил метод исследования, называемый вычислительным
экспериментом.
1.2 Схема вычислительного эксперимента
Технология исследования сложных проблем в этом методе состоит в по-
строении и анализе с помощью ЭВМ математической модели изучаемого объекта.
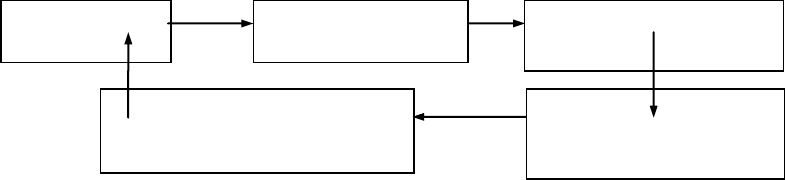
Схему вычислительного эксперимента можно представить следующим образом.
Основные этапы вычислительного эксперимента можно сравнить с соответ-
ствующим физическим экспериментом. На первой стадии вычислительного экс-
перимента на основе анализа исследуемого физического объекта делается его ма-
тематическое описание, т.е. выбирается математическая модель (в физическом
эксперименте этому этапу соответствует анализ и выбор схемы эксперимента,
Объект иссле-
дования
Математическая
модель
Численный метод (ал-
горитм)
Программирование для
ЭВМ
Проведение вычислений и
анализ результатов
2
уточнение элементов конструкции и самой установки). Далее выбирается чис-
ленный метод, составляется вычислительный алгоритм, исследуются вопросы
устойчивости и точности решения (в физическом эксперименте на этом этапе
осуществляется конструирование и изготовление экспериментальной установки,
ее отладка, калибровка). Затем осуществляются программирование и машин-
ный счет (в лабораторных условиях этому этапу соответствует проведение серии
экспериментальных измерений). На последнем этапе осуществляется анализ ре-
зультатов и уточнение модели, метода, программы. Такой же анализ результатов
с необходимыми корректировками конструкции экспериментальной установки и
схемы эксперимента проводится в лабораторных условиях.
При выборе физической и, следовательно, математической модели обычно
пренебрегают факторами, не оказывающими существенного влияния на иссле-
дуемый процесс. Типичные математические модели, соответствующие физиче-
ским явлениям, формулируются в виде уравнений математической физики. Вы-
числительный эксперимент служит мостом между теоретическими расчетами и
лабораторными экспериментами. Его применение служит мощным стимулом для
развития численных методов.
Под численным методом понимается такая интерпретация математической
модели, которая доступна для реализации на ЭВМ - так называемая “дискретная
модель”. Например, если математическая модель представляет собой дифферен-
циальное уравнение, то численным методом может быть аппроксимирующее его
разностное уравнение совместно с алгоритмом, позволяющим найти его решение.
Чтобы реализовать алгоритм, необходимо составить программу для ЭВМ.
После отладки программы следует проведение вычислений и анализ результатов.
Полученные результаты изучаются с точки зрения их соответствия исследуемому
явлению, при необходимости уточняется математическая модель, и вносятся ис-
правления в численный метод.
Такова в общих чертах схема вычислительного эксперимента; его основу
составляет триада: модель - метод (алгоритм) - программа. Можно указать такие
крупные области применения вычислительного эксперимента, как энергетика,
аэрокосмическая техника, ядерная физика.
1.3 Погрешности
Необходимо подчеркнуть, что процесс исследования исходного объекта
описанным выше методом неизбежно носит приближенный характер, т.к. на каж-
дом этапе вносятся те или иные погрешности. Так, построение математической
модели связано с упрощением исходного явления, недостаточно точным задани-
ем коэффициентов уравнений и других входных данных. Эти погрешности явля-
ются неизбежными в рамках данной модели и потому являются неустранимыми
по отношению к численному методу, реализующему данную модель.
3
При переходе от математической модели к численному методу возникают
погрешности, называемые погрешностями метода. Они связаны с тем, что лю-
бой численный метод воспроизводит математическую модель приближенно.
Наиболее типичными погрешностями метода являются погрешность дискрети-
зации и погрешность округления.
Обычно построение численного метода для заданной математической мо-
дели разбивается на два этапа:
а) формулировка дискретной задачи;
б) разработка вычислительного алгоритма, позволяющего отыскать решение дис-
кретной задачи.
Например, если исходная математическая задача сформулирована в виде
системы дифференциальных уравнений, то для численного решения необходимо
заменить ее системой конечного, может быть, очень большого числа линейных
алгебраических уравнений. Это происходит в результате замены непрерывной
области независимой переменной конечным множеством дискретных точек, в ко-
торых ищется решение. В этом случае говорят, что проведена дискретизация ис-
ходной математической задачи. Простейшим примером дискретизации является
построение разностной схемы путем замены дифференциальных выражений ко-
нечно-разностными аналогами. Ясно, что решение дискретной задачи отличается
от решения исходной задачи. Разность соответствующих решений и называется
погрешностью дискретизации.
Дискретная модель представляет собой систему большого числа алгебраи-
ческих уравнений. Невозможно найти решение такой системы точно и в явном
виде. Поэтому приходится использовать тот или иной численный алгоритм реше-
ния системы линейных алгебраических уравнений. Входные данные этой систе-
мы, а именно, коэффициенты и правые части задаются в ЭВМ не точно, а с ок-
руглением. В процессе работы алгоритма погрешности округления обычно нака-
пливаются, и в результате решение, полученное на ЭВМ, будет отличаться от
точного решения дискретной задачи. Результирующая погрешность называется
погрешностью округления (или вычислительной погрешностью).
Таким образом, следует различать погрешности модели и метода, реали-
зующего данную математическую модель, и при выборе метода (алгоритма) учи-
тывать вопросы погрешностей.
1.4 Требования к вычислительным методам
Одной и той же математической задаче можно поставить в соответствие
множество различных дискретных моделей, однако далеко не все из них пригод-
ны для практической реализации. Вычислительные алгоритмы, предназначенные
для ЭВМ, должны удовлетворять ряду требований. Можно выделить две группы
требований. Первая группа связана с адекватностью дискретной модели исходной
математической задаче, вторая - с реализуемостью численного метода на ЭВМ.
К первой группе относятся такие требования, как сходимость численного
метода, выполнение дискретных аналогов законов сохранения, качественно пра-

4
вильное поведение решения исходной задачи. Поясним сказанное. Предположим,
что дискретной моделью задачи является разностная схема, и при замене диффе-
ренциальных выражений конечными разностями получается большое число ал-
гебраических уравнений. Чем точнее мы хотим получить решение, тем меньше
нужно брать шаг сетки, или параметр дискретизации ( x), и тем большее число
уравнений приходится решать. Говорят, что численный метод сходится, если при
неограниченном увеличении числа уравнений ( х 0) решение дискретной зада-
чи стремится к точному решению исходной задачи. Далее, известно, что диффе-
ренциальные уравнения математической физики являются следствиями законов
сохранения. Поэтому естественно требовать, чтобы для разностной схемы выпол-
нялись аналоги таких законов сохранения. Разностные схемы, удовлетворяющие
этому методу, называются консервативными.
Вторая группа требований к численным методам связана с объемом опера-
тивной памяти ЭВМ, с возможностью получить решение соответствующей сис-
темы уравнений за приемлемое время, с устойчивостью алгоритма. Алгоритм на-
зывается устойчивым, если в процессе решения рост вычислительных погреш-
ностей ограничен сверху, и неустойчивым, если погрешности возрастают неог-
раниченно. Существуют также алгоритмы, которые устойчивы при выполнении
определенных условий для параметров дискретной модели. Такие алгоритмы на-
зываются условно устойчивыми. Ясно, что использовать следует устойчивые
или условно устойчивые алгоритмы.
Тема 2.Примеры математических моделей некоторых природных процессов.
Простая математическая модель для задачи об остывании тела.
2.1 Кинетика химических реакций
Для моделирования природных процессов часто используются дифферен-
циальные уравнения первого порядка. Можно представить себе одностадийную
химическую реакцию типа А В, где А – исходное вещество, В – конечный
продукт. Если С – концентрация вещества А, то ее убывание часто описывают
уравнением:
kC
dt
dC
(1)
где k – константа скорости реакции, а начальное условие задается как
С=С
0
при t = 0. Если k = const. (что не всегда выполняется), уравнение легко ин-
тегрируется: C=C
0
e
-kt
. Аналогичной формулой описывается закон радиоактивно-
го распада: N=N
0
e
- t
, где N
0
– начальная концентрация распадающегося радиоак-
тивного вещества, а - постоянная распада. Хотя поведение этих двух функций
описывается одним и тем же законом, константы соответствующих реакций мо-
гут отличаться на порядки: например, k глюкозы составляет 0,72 1/сут., а ра-
диоактивного углерода
14
С равна 3 10
-7
1/сут.
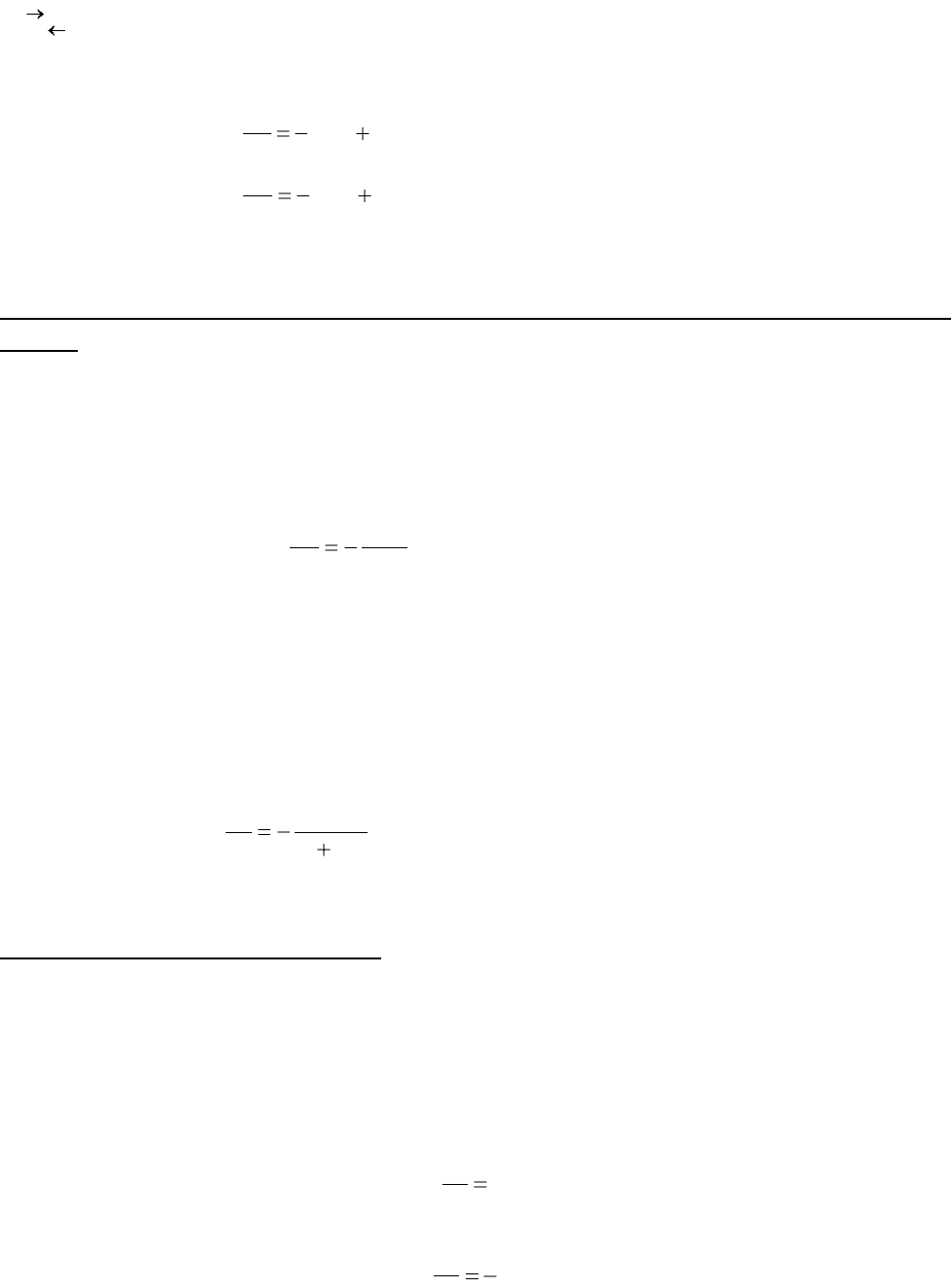
5
Зачастую одностадийные химические реакции бывают обратимыми:
А
В. Тогда для их математического описания потребуются две скорости реак-
ций: прямой и обратной. Если под символами A и В подразумевать соответст-
вующие концентрации, то процесс описывается двумя уравнениями:
AkBk
dt
dB
BkAk
dt
dA
1221
2112
(2)
при этом начальные концентрации А
0
, В
0
должны быть заданы. Понятно, что бо-
лее сложные взаимопревращения будут описываться большим числом реакций.
2.2 Изменение атмосферного давления с изменением расстояния от поверхности
Земли.
Примем следующие предположения для математической модели : 1) темпе-
ратура воздуха не зависит от высоты над поверхностью; 2) воздух является иде-
альным газом; 3) гравитационные силы подчиняются закону Ньютона. Тогда
можно показать, что давление Р на расстоянии х от центра Земли удовлетворяет
уравнению:
2
x
PK
dx
dP
p
(3),
причем на поверхности Земли (х=R) P(R)=1атм.
Здесь R – радиус Земли, K
p
=kM/cg (k – гравитационная постоянная, М – масса
Земли, g – ускорение свободного падения, с – константа). Если эти параметры
выбраны в одной и той же системе единиц, отношение K
p
/R=0.9.
Уравнение (3) удобно привести к безразмерному виду. Для этого введем новые
переменные: x=h+R, z=h/R, P(x)=P(R(1+z))=y(z). Так как z<<1, то пренебрегая
величиной z
2
, уравнение (3) сведем к виду:
)21(
9.0
z
y
dz
dy
(4)
(попробуйте провести эти преобразования самостоятельно). Начальное условие,
которое обеспечивает единственность решения, формулируется как у(0)=1.
2.3 Модель типа жертва-хищник
Основы взаимодействия между простыми популяциями типа жертва-
хищник непросто выразить математически. Лишь некоторые упрощающие пред-
положения позволяют это сделать. Пусть популяция кроликов будет жертвами,
популяция лис – хищниками. Предположим, что кроме кроликов лисы ничего не
едят (и потому не размножаются), а в отсутствие лис кролики размножаются не-
ограниченно. В этом случае скорость увеличения популяции кроликов будет
ax
dt
dx
,
а скорость уменьшения популяции лис
py
dt
dy
,

6
где t– время, a– коэффициент рождаемости кроликов, р– коэффициент смертно-
сти лис. Однако популяции взаимодействуют (парные взаимодействия, вклю-
чающие произведение ху). Тогда для кроликов
bxyax
dt
dx
(5)
где b – коэффициент, учитывающий уменьшение популяции кроликов вследствие
поедания их лисами. Для лис
pycxy
dt
dy
(6)
где с – коэффициент, учитывающий прирост популяции лис вследствие поедания
ими кроликов. Для решения системы должны быть заданы начальные размеры
популяций, а для получения правдоподобного результата – правдоподобные зна-
чения всех коэффициентов.
2.4 Задача об остывании тела
Рассмотрим подробнее теплофизическую задачу в упрощенной постановке.
Пусть нагретое тело помещено в среду, имеющую более низкую температуру Т
ср
.
Из опыта ясно, что тело будет остывать до тех пор, пока его температура не срав-
няется с температурой cреды, но как будет происходить процесс остывания со
временем? Для простоты рассмотрения предположим, что тело обладает высокой
теплопроводностью, так что температура быстро выравнивается по всему объему,
т.е. считаем, что равномерно нагретое тело будет так же равномерно остывать, и
задачу распределения температуры в объеме мы не рассматриваем. Это сущест-
венное упрощение модели явления, так как в этом случае температура является
функцией лишь одной переменной – времени t. Лучистым теплообменом также
пренебрежем, т.к. его вклад становится существенным при достаточно высоких
температурах.
Выберем некоторый момент времени t, в который температура достигла
значения Т>Т
ср
, и посмотрим, что произойдет за бесконечно малый промежуток
времени dt. За это время тело отдаст в среду c единицы поверхности количество
тепла, пропорциональное разности температур тела и среды (закон Ньютона-
Рихмана), и величине промежутка dt:
dQ = (T - T
ср
)dt.
С другой стороны, за это время тело понизит свою температуру на величину dT, и
если массовая теплоемкость тела равна с, а масса, сосредоточенная в объеме, ог-
раниченном поверхностью с единичной площадью равна m, то количество тепла
dQ, отданное телом, равно -mc dT. Тогда можем записать
-mc dT = (T - T
ср
)dt,
откуда
dT/dt = -r(T - T
ch
), (7)
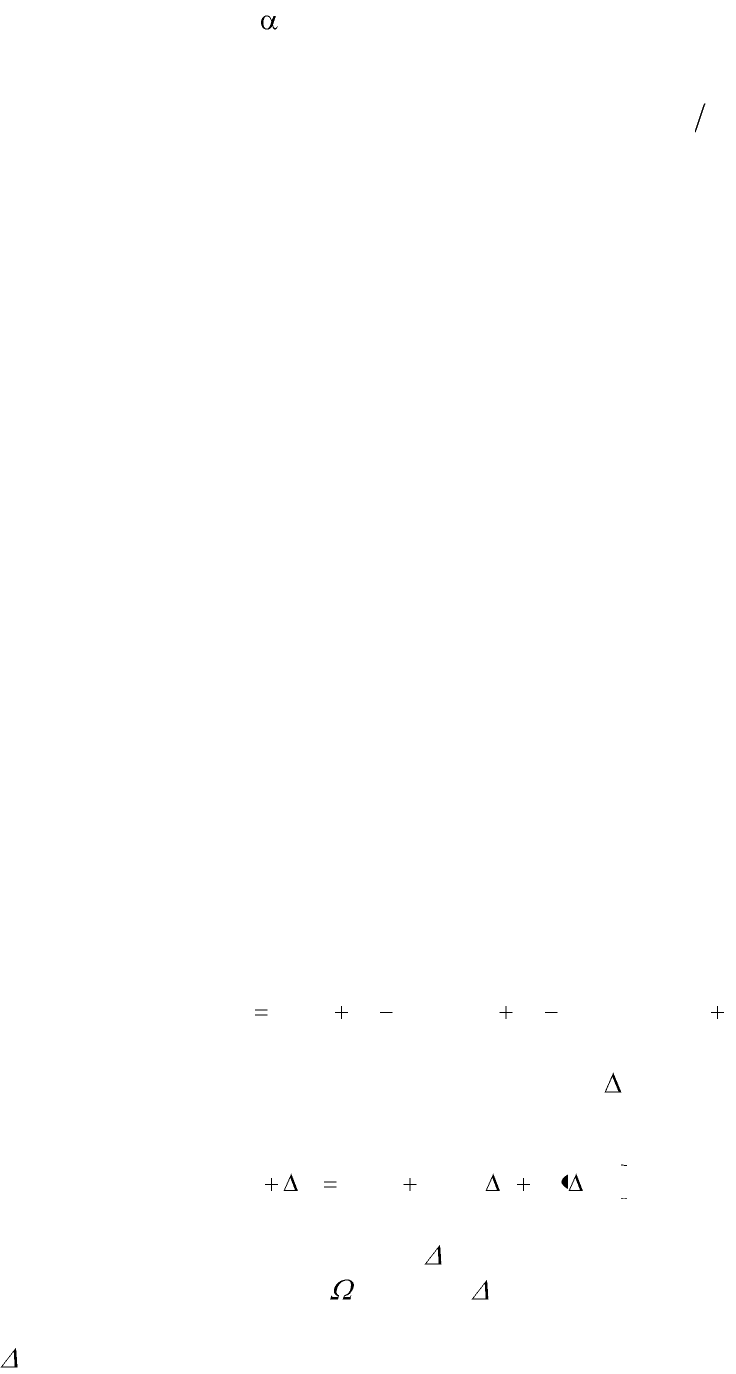
7
где коэффициент r = /mc назовем коэффициентом остывания.
Таким образом, мы получили математическую модель для задачи остыва-
ния тела в виде обыкновенного дифференциального уравнения первого порядка.
Для его решения необходимо иметь начальное условие: Т
t=0
= T
0
. Это уравнение
легко интегрируется, если коэффициент остывания r - константа, однако, если r
является некоторой функцией температуры (что вполне реально), то для решения
поставленной задачи приходится прибегать к численным методам.
Тема 3. Численные методы решения обыкновенных дифференциальных
уравнений и их систем.
3.1 Метод Эйлера
Полученная выше математическая модель явления остывания нагретого те-
ла является дифференциальным уравнением 1-го порядка. Рассмотрим численный
метод решения таких уравнений. Для этого запишем общий вид дифференциаль-
ного уравнения первого порядка с правой частью, являющейся функцией как пе-
ременной х, так и y(x):
dy(x)/dx = f(x,y) (1)
Уравнение может быть решено при задании начального условия y (0) = y
0
и об-
ласти изменения переменной x: x > 0.
Такая задача в математике называется задачей Коши. Вместо одного урав-
нения задача может описываться системой аналогичных уравнений. Заранее
предполагаем, что решение задачи Коши существует и единственно. Для числен-
ного решения обыкновенных дифференциальных уравнений обычно используют
разложение функции в ряд Тейлора:
...!2/)('')()(')()()(
0
2
0000
xyxxxyxxxyxy
(2)
Чем больше членов ряда будет использовано, тем точнее можно вычислить зна-
чение функции на некотором (малом) расстоянии х = x – x
0
от исходной точки.
Рассмотрим многошаговый разностный метод - метод Эйлера. В этом методе в
разложении (2) ограничиваются двумя членами ряда:
2
000
)()(')()( xOxxyxyxxy
(3)
Первым этапом является дискретизация задачи. Для этого введем по перемен-
ной х равномерную сетку с шагом х > 0, т.е. рассмотрим множество точек
= { х
n
= n х, n = 0,1,2,...},
х называется параметром дискретизации.
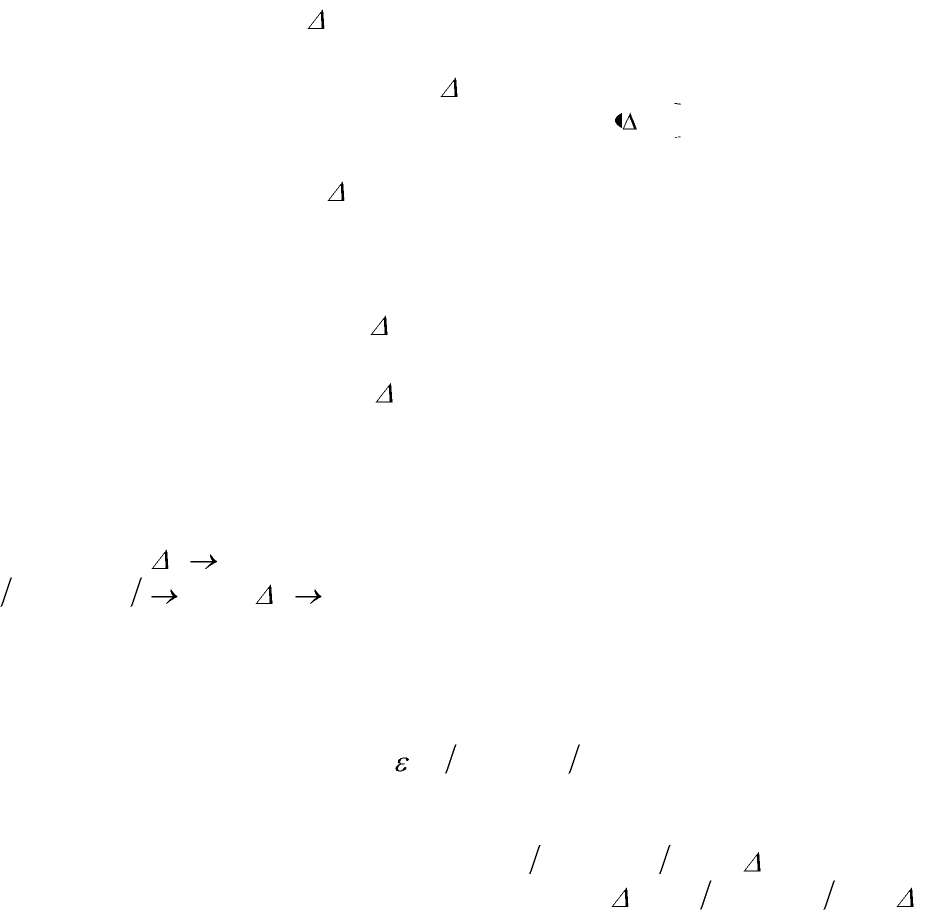
8
Будем обозначать точное решение задачи через y(х), а приближенное в точ-
ках сетки - через U(х
n
). Приближенное решение называется сеточной функцией,
т.к. оно определяется только в точках сетки (х
0
, х
1
, ...,х
n
,..).
Теперь заменим дифференциальное уравнение (1) разностным, для чего
выражение dy/dх выразим из разложения (3) в виде конечной разности, выбрав в
качестве х
0
произвольную точку x
n
и учитывая, что y’(x
n
) = f(x
n
,U
n
).
(U
n+1
- U
n
)/ х = f(х
n
,U
n
); n = 0,1,2,...; U
0
= y
0
(4)
Мы заменили точные значения у(х
n
+ х) и у(х
n
) на U
n+1
и U
n
соответственно, по-
скольку равенство (3) при отбрасывании остатка
2
)( xO
становится приближен-
ным. Решение уравнения (4) находится явным образом по рекуррентной формуле:
U
n+1
= U
n
+ х f(х
n
,U
n
); n = 0,1,2,...; U
0
= y
0
. (5)
Поскольку начальное условие задано, то имеем легко программируемую итераци-
онную формулу:
U
1
= U
0
+ х f(х
0
,U
0
) (U
0
= y
0
)
U
2
= U
1
+ х f(х
1
,U
1
)
и т.д. Таким образом, приближенное решение задачи найдено.
Основными вопросами при использовании численных методов являются
вопросы сходимости и точности решения. В методе Эйлера рассматривается схо-
димость при х 0. Говорят, что метод сходится в точке х
n
, если
y
n
- U(х
n
) 0 при х 0. Метод сходится на отрезке { 0, Х }, если он сходит-
ся в любой точке этого отрезка.
Погрешностью метода в данной точке х
n
называется абсолютная величина
разности между точным и приближенным решениями:
n
= y
n
- U(х
n
) .
Говорят, что метод имеет р-й порядок точности по параметру дискретиза-
ции, если существует число р > 0 такое, что y
n
- U(х
n
) = O{( х)
p
}. Доказано, что
метод Эйлера имеет первый порядок точности по х, т.е. y
n
- U(х
n
) = O( х).
Алгоритм Эйлера будет использоваться в дальнейшем при решении многих фи-
зических задач.
3.2 Метод Рунге-Кутты
Чтобы уменьшить погрешность решения, в разложении (2) функции в ряд
Тейлора нужно использовать большее количество членов. В серии методов
Рунге –Кутты используют для приближенных вычислений различное число чле-
нов ряда, получая тот или иной порядок точности. Алгоритм вычислений приво-
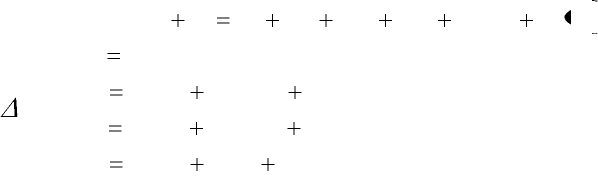
9
дят к виду, удобному для реализации на ЭВМ. Для наиболее часто используемого
метода четвертого порядка точности, учитывающего пять членов ряда, выведены
следующие формулы.
5
432100
6/)22()( hOkkkkyhxy
(6),
где h= x, а
),(
)2/,2/(
)2/,2/(
),(
3004
2003
1002
001
kyhxhfk
kyhxhfk
kyhxhfk
yxhfk
Реализация метода Рунге-Кутты на ЭВМ несколько сложнее, чем метода Эйлера,
но точность существенно выше. В Приложении даны примеры программ, реали-
зующих оба рассмотренных метода.
Тема 4. Применение метода Эйлера к решению уравнений движения Ньюто-
на.
4.1 Падение тел у земной поверхности
Рассмотрим пример одномерного движения - падение тел у земной поверх-
ности. Простейшее описание такого движения не учитывает внутренней структу-
ры тела, рассматривая его как некий идеализированный объект - материальную
точку. Хотя реальные тела точками не являются, для многих реальных задач та-
кое упрощение модели оправдано и дает реальное представление о скоростях,
времени падения и т.д. Для описания падения используется второй закон Ньюто-
на, который гласит, что ускорение движущегося тела определяется равнодейст-
вующей всех сил, действующих на тело:
m a(t,y) = F(t,y,v).
Этот закон может быть записан в виде дифференциального уравнения второго
порядка
d
2
y/dt
2
= F(t,y,v)/m
или в виде системы двух дифференциальных уравнений первого порядка, если
ввести ускорение a = F(t,y,v)/m:
dv/dt = a;
dy/dt = v(t,y).
Здесь m - масса тела, v - его скорость, a - ускорение, y - координата.
Если при падении не учитываются сопротивление воздуха и выталкивающая си-
ла, то единственной действующей на тело силой является сила тяжести, равная
mg, где g - ускорение свободного падения. В этом случае уравнение движения
имеет аналитическое решение.

10
Однако зачастую, особенно при падении тел в более плотных, чем воздух,
средах эти силы нужно учитывать. Как известно, выталкивающая сила равна весу
жидкости, вытесненной телом, поэтому ее учет прост и эквивалентен уменьше-
нию массы тела на величину
ср
V, где
ср
- плотность внешней среды, в которой
происходит падение, а V - объем тела. Сложнее обстоит дело с силой сопротивле-
ния среды, которая, по опытным данным, зависит от скорости тела v. Известны
две эмпирические зависимости силы сопротивления от скорости: F
сопр
= k
1
v и
F
сопр
= k
2
v
2
, где коэффициенты k
1
и k
2
зависят от свойств среды и геометрии тела.
Вернемся к падению тел у поверхности Земли, когда выталкивающей силой
можно пренебречь вследствие малой плотности воздуха. Равнодействующая сил,
действующих на тело, в этом случае равна
F = mg - F
сопр
.
Поскольку сила сопротивления возрастает с ростом скорости, то в процессе дви-
жения осуществляется некоторое значение скорости v = v
пред
,, при котором
F
сопр
= mg, что соответствует нулевому ускорению и, следовательно, установив-
шейся скорости, с которой дальше продолжается падение. Эта скорость называ-
ется предельной скоростью, и она является константой для рассматриваемой за-
дачи. Если известна зависимость F
сопр
(v), предельная скорость легко вычисляется,
и ее можно использовать вместо констант k
1
и k
2
в уравнениях движения.
4.2 Численное решение задачи о падении тела
Допустим для определенности, что нам известна зависимость силы сопро-
тивления от скорости в виде: F
сопр
= kv
2
. Тогда суммарная действующая на тело
сила равна
F = mg - kv
2
= ma, и
a = (mg - kv
2
)/m. (1)
Представим математическую модель задачи в виде системы двух уравнений 1-го
порядка:
dv/dt = a (2)
dy/dt = v (3).
Начальные условия: v
t=0
= 0, y
t=0
= 0 (при соответствующем выборе системы ко-
ординат). Следуя методу Эйлера, заменяем дифференциальные выражения в
уравнениях (2) и (3) их разностными аналогами (с учетом выражения (1) для ус-
корения):
(v
n+1
- v
n
)/ t = a
n
(y
n+1
- y
n
)/ t = v
n
откуда
v
n+1
= v
n
+ a
n
t (4)
