Ивания С.П. Математическое моделирование физических процессов
Подождите немного. Документ загружается.

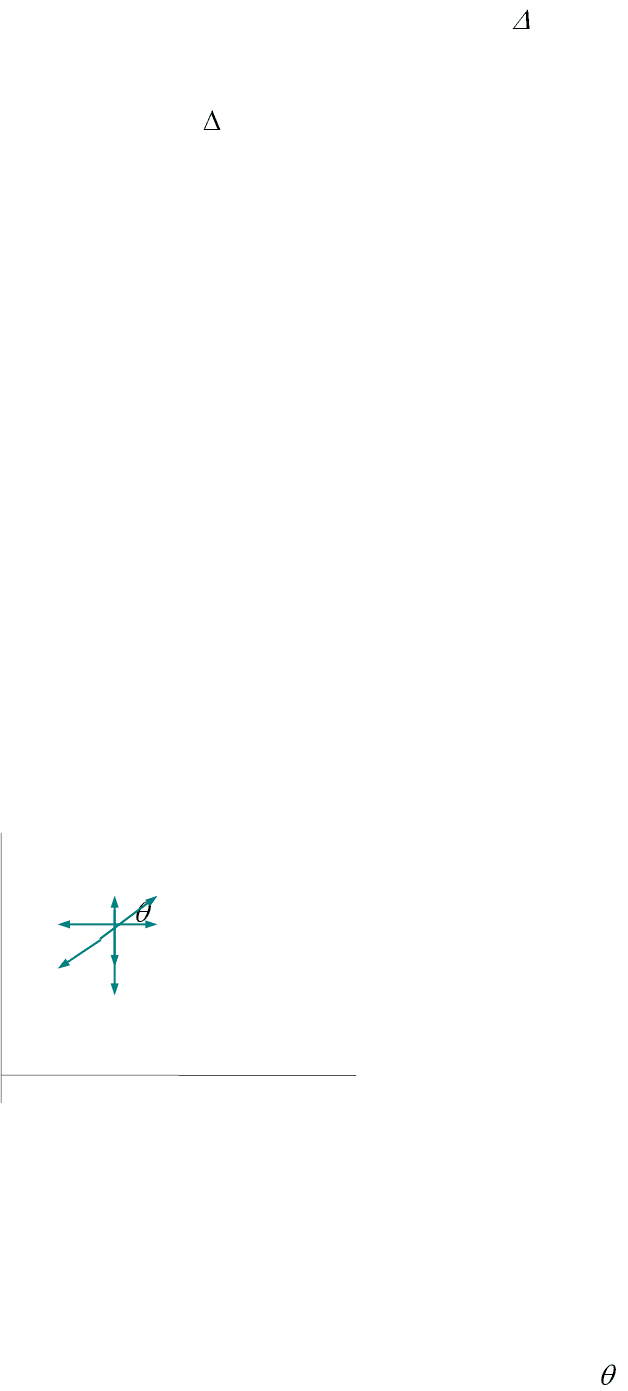
11
y
n+1
= y
n
+ v
n
t (5)
Для решения системы (4), (5) два начальных условия у нас имеются.
Шаг по времени t нужно выбирать достаточно малым, чтобы замена дифферен-
циального выражения его разностным аналогом не привела к большой погрешно-
сти. Оценить погрешность метода можно, если применить полученный алгоритм
к задаче, в которой сопротивлением воздуха можно пренебречь, т. е. имеется ана-
литическое решение.
Примечание: студент должен понимать, что из уравнений (4), (5) мы фактиче-
ски получаем значения сеточных функций для скорости и координаты, а не их
точные значения; мы не стали вводить новых обозначений для сеточных функ-
ций, чтобы не увеличивать количество символов.
4.3 Двумерные траектории. Численное решение задачи о движении тела, брошен-
ного под углом к горизонту, с учетом силы сопротивления
Как известно, сила, ускорение, скорость - это величины векторные, и в об-
щем случае второй закон Ньютона следует записывать в векторной форме:
F = ma.
Рассмотрим тело, брошенное под углом к горизонту, и силы, действующие на не-
го в произвольной точке траектории.
У
v
y
v
v
x
F
сопр
mg
Х
Сила сопротивления всегда направлена противоположно скорости движения v.
Разложим скорость на две компоненты v
x
и v
y
и запишем уравнения движения для
этих компонент. При этом учтем, что в направлении У действуют две силы: сила
тяжести mg и проекция силы сопротивления F
сопр
на ось У; в направлении Х дей-
ствует одна сила – это проекция силы сопротивления на ось Х. Силу сопротивле-
ния по прежнему считаем пропорциональной квадрату скорости. Тогда имеем:
mdv
x
/dt = -F
сопр
cos
12
mdv
y
/dt = -mg - F
сопр
sin
С учетом того, что F
сопр
=kv
2
, vcos = v
x
, vsin = v
y
и вводя коэффициент k/m = A,
перепишем эту систему в виде:
dv
x
/dt = -Avv
x
(6)
dv
y
/dt = -g - Avv
y
. (7)
Чтобы получить траекторию частицы, к системе (6), (7) надо добавить пару урав-
нений
dx/dt = v
x
(8)
dy/dt = v
y
(9)
и решать их совместно. Применяя метод Эйлера, введем сетку по времени с ша-
гом t и заменим в (6) - (9) дифференциальные выражения конечными разностя-
ми; окончательно для вычисления сеточных функций компонент скоростей и ко-
ординат получим выражения:
v
xn+1
= v
xn
- Av
n
v
xn
t
x
n+1
= x
n
+ v
xn
t
v
yn+1
= v
yn
- (g+Av
n
v
yn
) t
y
n+1
= y
n
+ v
yn
t.
При использовании этих уравнений следует обратить внимание на то, что
на каждом шаге кроме х- и у- компонент скорости нужно вычислять
v
n
2
= v
xn
2
+ v
yn
2
и модуль скорости v
n
= v
xn
2
+v
yn
2
, т.к. он входит в соответст-
вующие формулы для компонент скоростей. Понятно, что для решения задачи
необходимо иметь начальные условия: начальную скорость v
0
, начальные коор-
динаты x
0
, y
0
и начальный угол
0
, что позволит задать начальные скорости в на-
правлениях обеих осей.
Тема 5. Учет силы сопротивления среды при решении уравнений движения
Ньютона
5.1 Режимы течения. Вязкость. Число Рейнольдса.
Из самых общих соображений при движении в различных средах сила со-
противления движению может зависеть как от формы тела (обтекаемая или нет),
так и от свойств среды, например, плотности, вязкости.
Вязкость определяет силу внутреннего трения жидкости (газа), которая была оп-
ределена Ньютоном как
F
тр
= ( v/ z)S,
13
где v- изменение скорости между слоями жидкости, находящимися на расстоя-
нии z между собой, S - площадь поверхности соприкасающихся слоев, - коэф-
фициент пропорциональности, называемый коэффициентом динамической вяз-
кости (или просто динамической вязкостью). Размерность , как это легко вы-
вести из приведенной выше формулы, есть Па с. Наряду с коэффициентом дина-
мической вязкости часто используется коэффициент кинематической вязкости
= /
„
, где
„
- плотность жидкости (газа). Размерность кинематической вязко-
сти есть м
2
/c, что также легко вывести. Вязкость наряду со скоростью и размером
движущегося тела определяет режим течения. Если перейти в систему координат,
связанную с телом, можно считать, что тело покоится, а его обтекает поток жид-
кости (или газа), о режиме течения которого мы и говорим.
Режим течения может быть ламинарным или турбулентным в зависимо-
сти от числа Рейнольдса Re, которое определяется как
Re = vl/ = vl
‘
/ .
Здесь l - характерный размер тела, v - его скорость относительно потока,
‘
-
плотность жидкости (газа). При Re<<1 (малые скорости и размеры, большая вяз-
кость) течение спокойное, без завихрений, траектории выделенных частиц жид-
кости не пересекаются и повторяют линии тока. Такой режим течения называется
ламинарным. При Re>>1 скорости велики, вокруг тела создаются вихри, за тра-
екторией выделенной частицы жидкости трудно проследить. Такой режим тече-
ния называется турбулентным.
5.2 Формула Стокса
Для ламинарного режима (Re<<1) и шарообразной формы тела аналитиче-
ская формула для силы сопротивления получена ученым Стоксом и носит назва-
ние формулы Стокса:
F
сопр
= 6 rv (1)
где - коэффициент динамической вязкости среды; r - радиус шара;
v - его скорость относительно потока cреды. Итак, формула, или закон, Стокса
получена для медленного поступательного движения шара в неограниченной вяз-
кой среде. Законом Стокса пользуются в коллоидной химии, молекулярной физи-
ке, физике аэрозолей. По закону Стокса можно определить скорость осаждения
мелких капель тумана, частиц ила, коллоидных и аэрозольных частиц. Условие
его применения: Re<~1.
Определим предельную скорость при падении частицы, если сила сопро-
тивления определяется формулой Стокса. Сила тяжести равна Vg , где V, - объ-
ем и плотность материала частицы; подъемная сила равна Vg
‘
, где
‘
- плот-
ность среды. Подъемная сила и сила сопротивления направлены противоположно

14
скорости падения, а для установившегося движения сумма всех действующих сил
равна нулю. Отсюда
Vg( -
‘
) = 6 rv
пр
Подставив выражение для объема частицы V = 4/3 r
3
, получим
v
пр
= 2/9( -
‘
)r
2
g/ . (2)
Если речь идет о падении шарика в воздухе, то плотностью воздуха можно пре-
небречь по сравнению с плотностью материала шарика, однако при падении в бо-
лее плотных средах (например, в воде) формулу (2) следует использовать в пол-
ном виде. Порядки величин динамической вязкости для разных сред таковы:
Среда
[mПа с]
Воздух
0,0182
Вода
1,002
Глицерин
1480
Оценки показывают, что при расчете скорости падения в воздухе формула Стокса
справедлива лишь для частиц микронных размеров. Предлагается сделать эти
оценки самостоятельно.
5.3 Сила гидравлического сопротивления
В другом предельном случае - Re>>1 - также получена эмпирическая фор-
мула для силы сопротивления движению. Она носит название силы гидравличе-
ского сопротивления.
F
сопр
= СSv
2 ‘
/2 (3)
Здесь С - безразмерный коэффициент, зависящий от формы тела;
S- наибольшее сечение тела в плоскости, перпендикулярной потоку, [м
2
];
‘
- плотность среды, [кг/м
3
];
v - относительная скорость движения тела в среде, [м/c].
Приближенные значения коэффициента С для тел различной формы:
Тело
С
1.Плоская пластина, перпендикулярная потоку
1,11
2.Открытая полусфера отверстием навстречу потоку
1,33
3.Открытая полусфера отверстием по потоку
0,35
4.Шар
0,20
5.Хорошо обтекаемое тело
0,05
15
Получим формулу для предельной скорости при падении тела, если для
учета сопротивления движению используется формула гидравлического сопро-
тивления. При установившемся движении равнодействующая всех действующих
на тело сил равна нулю, откуда следует
V( -
‘
)g = Cav
пр
2 ‘
/2
и v
пр
2
= 2V( -
‘
)g/(CA
‘
). (4)
Пренебрегать плотностью среды в числителе формулы (4) можно только в случае
газовых сред, когда >>
„
, но для движения массивного тела, например, в воде
такое пренебрежение приведет к ощутимой ошибке. Оценки показывают, что
применение формулы гидравлического сопротивления справедливо для расчета
движения реальных макроскопических тел в реальных средах. Попробуйте сде-
лать эти оценки самостоятельно.
Тема 6. Простые задачи нерелятивистской динамики заряженных частиц в
электрическом и магнитном полях. Применение численных методов.
6.1 Порядки величин в гауссовой системе единиц (CGSE)
Когда речь идет об электромагнитном взаимодействии, удобно пользовать-
ся гауссовой системой единиц, в которой в качестве основных приняты единицы
длины, массы и времени: см, г, с. Единицей измерения силы является дина: дина
= [г см/c
2
]. Тогда единицу заряда можно получить, пользуясь законом Кулона:
F = q
1
q
2
/r
2
откуда размерность [q] = г
1/2
см
3/2
c
-1
. Такую единицу называют электростатиче-
ской единицей заряда CGSE. Основные частицы, с которыми мы будем иметь
дело, это электрон и протон. Заряд электрона q
e
= -4,8 10
-10
ед.CGSE, заряд про-
тона q
p
равен той же величине с противоположным знаком. Эти заряды называ-
ются в атомной физике элементарными зарядами. Величина элементарного за-
ряда в системе СИ равна 1,6 10
-19
Кл. Массы элементарных частиц m
e
= 0,91 10
-27
г,
m
p
= 1,67 10
-24
г.
Сила, действующая в электрическом поле на единичный заряд, называется
напряженностью Е электрического поля в данной точке. Если же заряд имеет
величину q, то действующая на него сила в электрическом поле напряженностью
Е равна
F
E
= q E.
Таким образом, направление действующей на заряд силы совпадает с направле-
нием напряженности электрического поля. Размерность напряженности [E]
обычно определяют через потенциал, для которого в гауссовой системе введена
специальная единица - ед.потенциала CGSE: [E] = ед.потенциала CGSE/ см.

16
Если же движущаяся заряженная частица помещена в магнитное поле, то
на нее действует сила
F
B
= q/c v B.
В выражение для силы входит константа с = 3 10
10
см/c - скорость света; В - ин-
дукция магнитного поля; сила направлена перпендикулярно плоскости, образо-
ванной векторами v и В (векторное произведение), поэтому, если v B, то сила
F
B
= 0. Таким образом, на частицу, движущуюся вдоль магнитного поля, магнит-
ная сила не действует, так же как и на покоящуюся частицу. Размерность индук-
ции магнитного поля В в гауссовой системе совпадает с размерностью напряжен-
ности электрического поля Е, однако для нее есть специальное название Гаусс
(Гс). Соотношение между рассмотренными величинами в гауссовой системе и
системе СИ таково:
Величина
Система СИ
Гауссова система
F
Н
дина
E
В/м
ед.потенциала СGSE/см
B
Вебер/м
2
= Тесла
Гс
F(H)10
5
= F(дин); Е(В/м)10
4
/3 = Е(ед.пот.CGSE/см); В(Тесла)10
4
=В(Гс).
1дина = 10
-5
Н; 1 Гс = 10
-4
Тесла.
Пример: Небольшой лабораторный электромагнит создает магнитное поле с ин-
дукцией ~ 10
4
Гс; электрон влетает в поле со скоростью, в 100 раз меньшей ско-
рости света, перпендикулярно магнитному полю. Какова величина силы, дейст-
вующей на электрон ?
F = q
e
vB/c = q
e
B/100 = 4,8 10
-8
дин =4,8 10
-13
Н.
При наличии электрического и магнитного полей суммарная сила, действующая
на движущуюся заряженную частицу, равна
F = qE + q/c v B. (1)
Эта сила называется силой Лоренца. Пользуясь вторым законом Ньютона и вы-
ражением для силы Лоренца, мы можем рассмотреть задачи о движении заряжен-
ных частиц в электрическом и магнитном полях. В дальнейшем будем предпола-
гать, что Е и В однородны, т.е. не зависят от положения частицы в пространстве,
однако они могут не быть постоянными, т.е. допускается зависимость полей от
времени.
6.2 Заряженная частица в электрическом поле

17
Рассмотрим два простых случая, когда задача о траектории частицы имеет
аналитическое решение.
1. Однородное и постоянное электрическое поле
Запишем второй закон Ньютона в виде
ma = qE, a = q/m E.
Направим ось Х вдоль поля, тогда в дифференциальной форме можем записать:
d
2
x/dt
2
= q/m E.
Дифференциальное уравнение второго порядка может быть проинтегрировано
при наличии двух начальных условий:
х
t=0
= x
0
; dx/dt
t=0
= v
t=0
= v
0
.
Последовательно интегрируя, получим выражения для скорости и координаты
частицы:
v = v
0
+ (q/m) Et
x = x
0
+ v
0
t + (q/m) E t
2
/2.
2.Однородное периодически меняющееся во времени электрическое поле. Пусть
поле направлено по прежнему по оси Х, но зависит от времени по гармоническо-
му закону: Е = Е
0
sin t, где Е
0
- амплитуда поля, - его частота. Для частицы с
массой m и зарядом q второй закон Ньютона в дифференциальной форме:
d
2
x/dt
2
= (q/m) E
0
sin t.
Удобнее для интегрирования записать это уравнение в виде системы двух урав-
нений:
dv/dt = (q/m) E
0
sin t (2)
dx/dt = v (3)
Интегрирование возможно при наличии двух начальных условий:
x
t=0
= x
0
; v
t=0
= v
0
. Пусть в начальный момент частица покоилась, тогда
интегрирование уравнения (2) дает:
v = -(qE
0
/m ) cos t + C
1
,
где константа С
1
определяется из начального условия:: при t = 0 v = 0;
подстановка начального условия дает С
1
= qE
0
/m , и выражение для скорости

18
v = qE
0
/m - (qE
0
/m ) cos t (4)
Интегрирование уравнения (3) с использованием (4) дает
х = (qE
0
/m ) t - (qE
0
/m
2
)
sin t + C
2
,
где константа С
2
определяется из условия, что х = х
0
при t = 0.
Окончательно
x = x
0
+ (qE
0
/m ) t - (qE
0
/m
2
) sin t.
Итак, мы получили следующий результат: движение частицы в периодическом
электрическом поле складывается из поступательного движения и колебания;
скорость равна сумме скоростей поступательного движения и скорости колеба-
ний.
6.3 Заряженная частица в постоянном магнитном поле
Пусть электрическое поле равно нулю, а магнитное поле направлено вдоль
оси Z. Уравнение движения частицы с зарядом q и скоростью v записывается в
виде:
dv/dt = (q/mc) v B (5)
Чтобы рассчитать траекторию, уравнение (5) нужно записать в виде проекций на
оси X, Y и Z, для чего раскрыть векторное произведение. Поскольку В имеет
только одну компоненту В вдоль оси Z, векторное произведение упрощается, а
именно, его Z-компонента равна нулю, т.е. dv
z
/dt = 0 и v
z
= const, а для X- и Y-
компонент получаем следующие выражения:
dv
x
/dt = (Bq/mc) v
y
(6)
dv
y
/dt = -(Bq/mc) v
x
(7)
Систему (6) - (7) можно решить аналитически, и это удобно сделать, введя ком-
плексную величину v = v
x
+ i v
y
. Домножим уравнение (7) на i и сложим с (6).
После простых преобразований получим:
dv /dt = -i
c
v , (8)
где множитель
с
= Bq/mc. Уравнение (8) легко интегрируется:
v = v
0
exp (-i
c
t) (9),
где, предположим, v
0
– действительная скорость, направленная в начальный мо-
мент по оси Х.
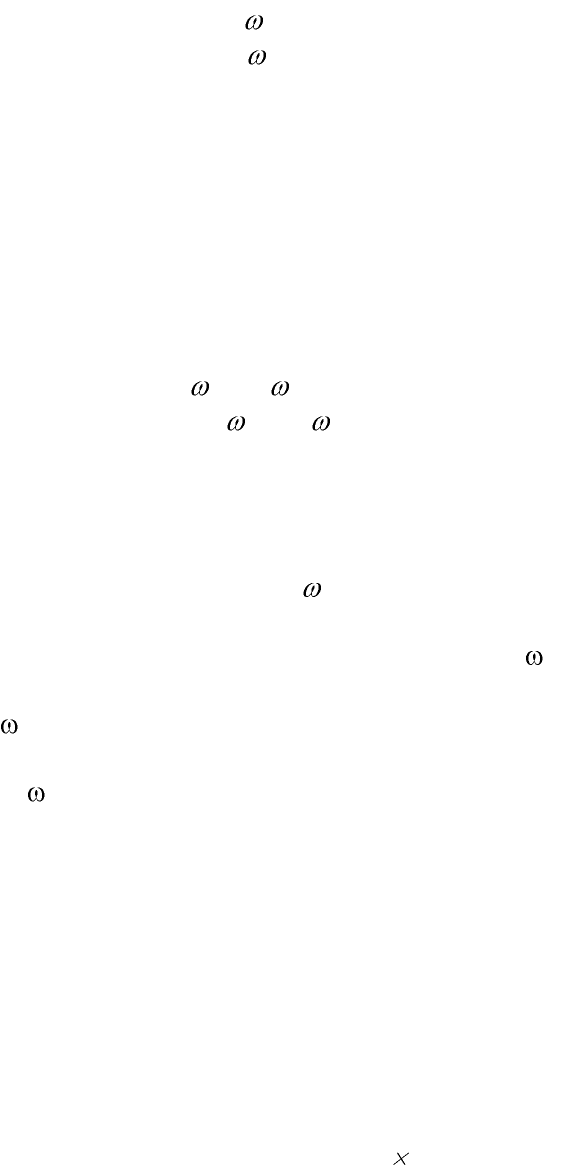
19
Теперь вернемся к действительным физическим величинам, раскрывая экспонен-
ту в (9):
v
x
= v
0
cos
c
t
v
y
= -v
0
sin
c
t
При этом v
x
2
+ v
y
2
= v
0
2
, т.е. сохраняется сумма квадратов скоростей, или кинети-
ческая энергия частицы. Дальнейшее интегрирование
dx/dt = v
x
x
t=0
=0
dy/dt = v
y
y
t=0
=0
приводит к следующим формулам для траектории частицы x = x(t),
y = y(t):
x = (v
0
/
c
)sin
c
t
y = v
0
/ω
c
+ (v
0
/
c
)cos
c
t
Легко видеть, что эта траектория представляет собой окружность в плоскости
ХУ, перпендикулярной магнитному полю:
x
2
+ (y - v
0
/ω
c
)
2
= (v
0
/
c
)
2
.
Итак, частица в однородном магнитном поле вращается с частотой
с
= qB/mc
вокруг направления В в плоскости, перпендикулярной направлению магнитного
поля. Частота вращения
с
называется циклотронной, или Ларморовской, часто-
той – по имени ученого, занимавшегося исследованиями плазмы. Радиус описы-
ваемой окружности R = v
0
/
c
называется циклотронным (или Ларморовским) ра-
диусом. Заметим, что на скорость движения частицы вдоль направления В маг-
нитное поле влияния не оказывает, поэтому если в начальный момент частица
имела компоненту скорости вдоль оси Z, то эта скорость у нее сохранится, и тра-
ектория частицы будет винтовой линией.
6.4 Общий случай: электрическое и магнитное поля произвольного вида
В общем случае произвольного поля используем выражение для силы Ло-
ренца (1) и запишем уравнение движения в виде
dv/dt = a, где a = (q/m) E + (q/mc) v B.
Поскольку все величины векторные, мы должны записать проекции уравнения
движения на оси координат
dv
x
/dt = a
x
20
dv
y
/dt = a
y
dv
z
/dt = a
z
,
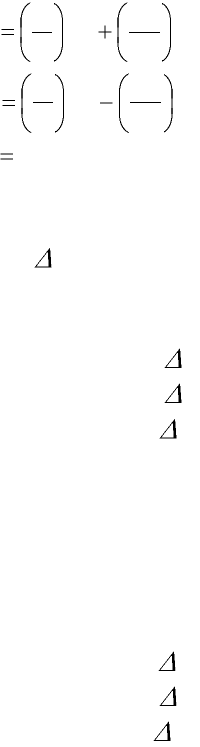
(для чего нужно правильно раскрыть векторное произведение). Для конфигура-
ции электромагнитного поля, когда вектор В направлен по оси Z, а электрическое
поле лежит в плоскости ХУ, эти компоненты равны:
0
z
xyy
yxx
a
Bv
mc
q
E
m
q
a
Bv
mc
q
E
m
q
a
Если уравнения не решаются аналитически, следует применить один из числен-
ных методов, например, метод Эйлера. Для этого область изменения переменной
t разобьем на N интервалов с шагом t и заменим в уравнениях дифференциаль-
ные выражения их конечно-разностными приближениями, после чего получим
итерационные формулы для скоростей в точках сетки:
v
xn+1
= v
xn
+ a
xn
t
v
yn+1
= v
yn
+ a
yn
t
v
zn+1
= v
zn
+ a
zn
t.
Чтобы получить траекторию частицы (x = x(t), y = y(t), z = z(t)), нужно записать
скорости в виде производных от соответствующих координат, и, следуя той же
процедуре замены дифференциальных выражений разностными, получим итера-
ционные формулы для координат:
x
n+1
= x
n
+ v
xn
t
y
n+1
= y
n
+ v
yn
t
z
n+1
= z
n
+ v
zn
t.
Для решения этих уравнений необходимо иметь начальные условия
v
t=0
= v
0
и начальные значения координат x
0
, y
0
, z
0
.
Примечание: не всегда метод Эйлера дает достаточную точность для решения
описанных выше задач. Поэтому в лабораторной работе №3 наряду с методом
Эйлера применен метод Рунге-Кутты, имеющий более высокий порядок точно-
сти.
Тема 7. Линейные и нелинейные колебательные системы
7.1.Введение.
Огромное количество явлений природы имеет периодический характер:
пульсирует излучение звезд; колебания и волны наблюдаются на поверхности во-
доемов; внутри любого организма бьется сердце и пульсирует кровь; с помощью
